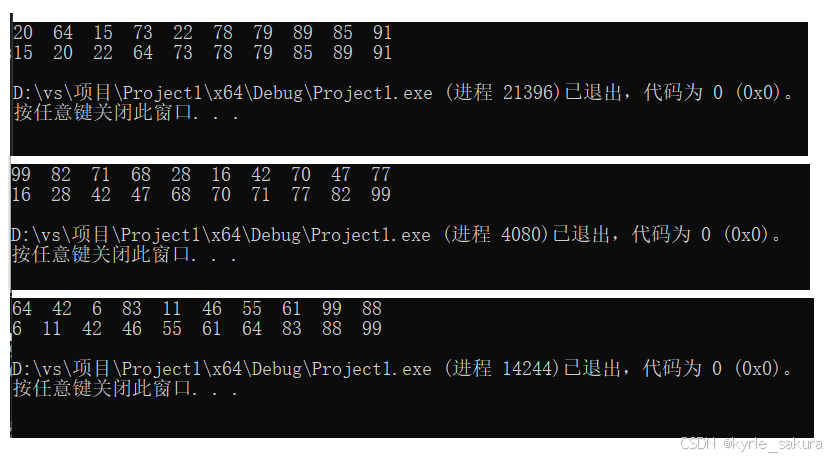
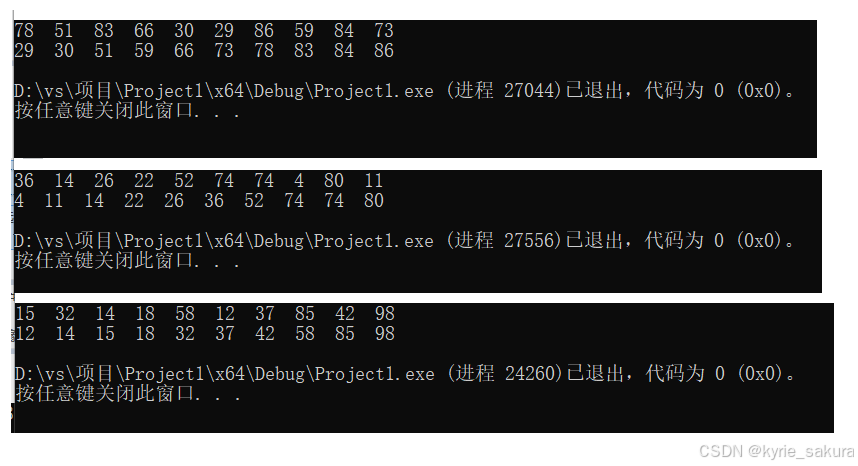
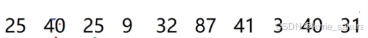普通排序算法
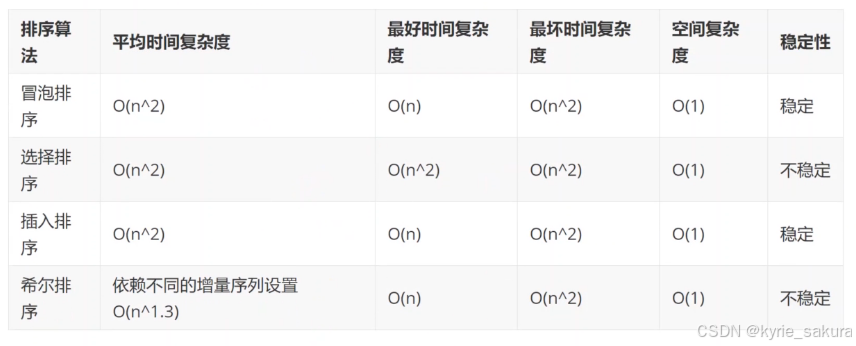
各排序性能对比:
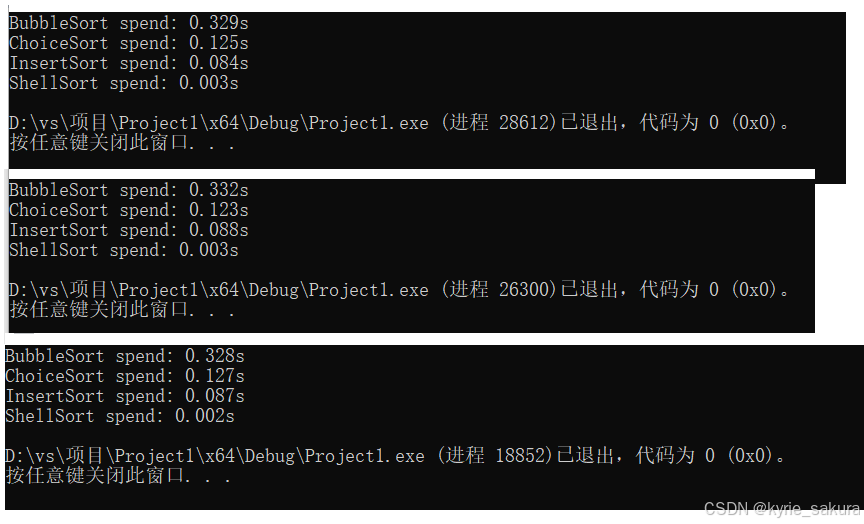
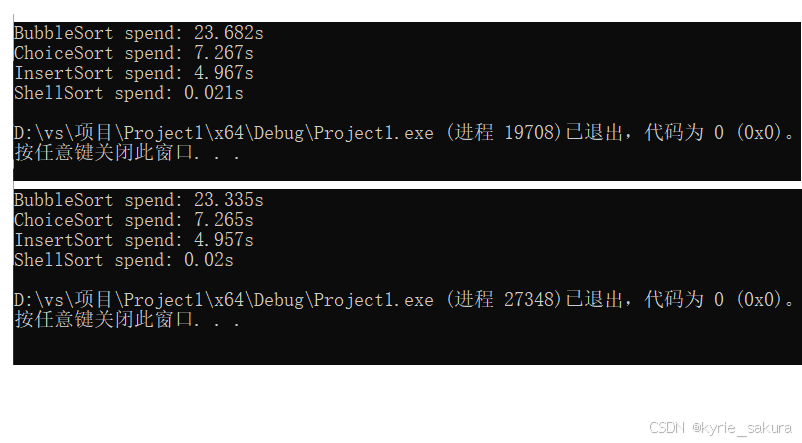
插入排序的效率最好,尤其是在数据已经趋于有序的情况下,采用插入排序效率最高。
一般中等数据量的排序都用希尔排序,选择合适的增量序列,效率就已经不错了,
如果数据量比较大,可以选择高级的排序算法,如快速排序。也可以多种排序结合使用。
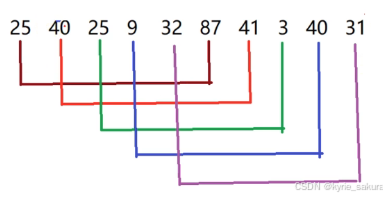
稳定性:在原始的数据序列中,相同元素,经过排序后,他们的前后顺序并没有改变,否则,称之为不稳定的排序。
稳定性对于单个数据无影响,但对于
例如数据5_5,排序过后为 5_6_7_5。两个两个5的位置改变了,但前后顺序并没有变动,这次排序是稳定的排序。
(虽然这两个值一样,但对于有关联的数据和C++的map映射表键值对有关联的数据来说,假设 原始数据5_5,其中前一个五映射数据aaa,后一个映射数据bbb。
在原始的序列当作,两个5存在映射关系,这里将左边的叫做k,右边的叫做value,当最开始在原始序列里面放置数据的时候,如果建相同,这里表现为都为5,是按照他们的字典顺序进行排列,这里体现为aaa在前面,bbb在后面。这样一查看筛选5,用5筛选k,对应的value都是按字典序排好的,如果是个稳定的排序,那么5对应的value的前后位置,还是按照对应的字典序排序的。)
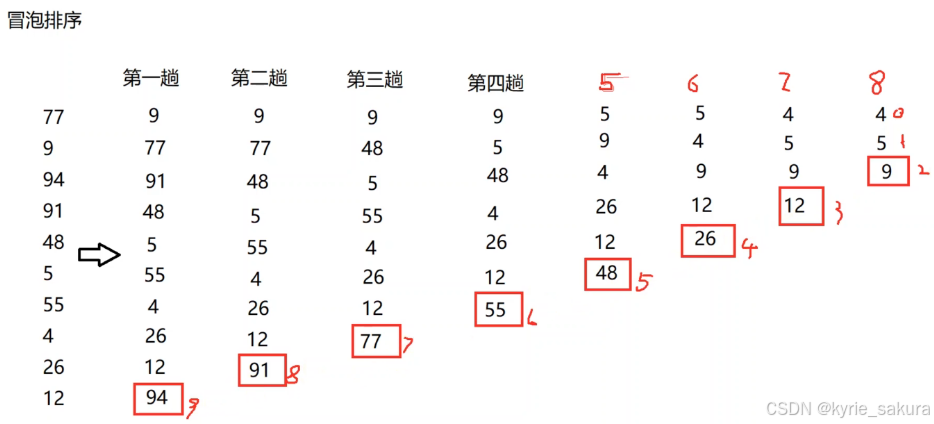
1、冒泡排序算法
理论
特点
相邻元素两两相比,把值大(小)的元素往下交换。
缺点
冒泡排序是所有排序算法效率最低的,原因在于,数据交换的次数太多!!
稳定性分析
在原始的数据序列中,相同元素,经过排序后,他们的前后顺序并没有改变,否则,称之为不稳定的排序。
代码
#include<iostream>
#include<stdlib.h> //包含随机数函数srand
#include<time.h> //需要用time作为随机数种子
using namespace std;
//冒泡排序算法
void BubbleSort(int arr[], int size)
{
for (int i = 0; i < size; i++)//趟数
{
//一趟的处理
//进行优化,如果某趟没有进行如何的数据交换,那么说明数据已经有序
bool flag = false;
for (int j = 0; j < size - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = true;
}
}
if( !flag )
//if (flag = false)
{
//如果没有做任何的数据交换,那么说明数据已经有序了
return;
}
}
}
int main()
{
int arr[10];
srand(time(NULL));
for (int i = 0; i < 10; i++)
{
arr[i] = rand() % 100 + 1;
}
for (int v : arr)
{
cout << v << " ";
}
cout << endl;
BubbleSort(arr, sizeof(arr) / sizeof(arr[0]));
for (int v : arr)
{
cout << v << " ";
}
cout << endl;
return 0;
}
测试
2、选择排序
特点
每次在剩下的元素中选择值最小(大)的元素,和当前元素进行交换。
缺点
相比于冒泡排序,交换的次数少了,但是比较的次数依旧很多。
代码实现
#include<iostream>
#include<stdlib.h> //包含随机数函数srand
#include<time.h> //需要用time作为随机数种子
using namespace std;
//选择排序算法 时间复杂度O(n^2) 空间复杂度O(n)
void ChoiceSort(int arr[], int size) //O(n^2)
{
for (int i = 0; i < size-1; i++)//O(n)
{
int min = arr[i];
int k = i;
for (int j = i+1; j < size; j++) //O(n)
{
if (arr[j] < min)
{
min = arr[j];
k = j;
}
}
//找到后面剩余序列中的最小值,和开始位置的值进行交换
if (k != i)
{
int tmp = arr[i];
arr[i] = arr[k];
arr[k] = tmp;
}
}
}
int main()
{
int arr[10];
srand(time(NULL));
for (int i = 0; i < 10; i++)
{
arr[i] = rand() % 100 + 1;
}
for (int v : arr)
{
cout << v << " ";
}
cout << endl;
ChoiceSort(arr, sizeof(arr) / sizeof(arr[0]));
for (int v : arr)
{
cout << v << " ";
}
cout << endl;
return 0;
}
测试
3、插入排序
特点
从第二个元素开始(默认第一个元素有序),把前面的元素序列当作已经有序,然后找合适的位置插入。
优点
在数据越趋于有序的情况下,插入排序是所有排序算法中最高的。
在基础排序算法中,插入排序是普通排序里面效率最高的排序算法,插入排序>冒泡排序&选择排序。
不仅仅没有交换,而且比较的次数也少。
代码实现
//插入排序
//时间复杂度: 最坏、平均 O(n^2) 最好O(n) 空间:O(1) 稳定性:稳定的
void InsertSort(int arr[], int size)
{
for (int i = 1; i < size; i++)//O(n)
{
int val = arr[i];
int j = i - 1;
for (; j >= 0; j--) //O(n)
{
if (arr[j] <= val)
{
break;
}
arr[j + 1] = arr[j];
}
//val -> j+1
arr[j + 1] = val;
}
//error 这样产生了交换是不是插入排序
/*for (int i = 0; i < size - 1; i++)
{
for (int j = i; j >= 0; j--)
{
if (arr[j + 1] >= arr[j])
{
break;
}
else
{
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}*/
}
测试
int main()
{
int arr[10];
srand(time(NULL));
for (int i = 0; i < 10; i++)
{
arr[i] = rand() % 100 + 1;
}
for (int v : arr)
{
cout << v << " ";
}
cout << endl;
InsertSort(arr, sizeof(arr) / sizeof(arr[0]));
for (int v : arr)
{
cout << v << " ";
}
cout << endl;
return 0;
}
4、希尔排序
特点
可以看作是多路的插入排序,分组的数据越趋于有序,整体上的数据也越趋于有序,插入排序效率完美体现。
前要:对于插入排序,如果数据趋于有序,那么插入排序是所有算法中,效率最高的排序算法。
希尔可以看作是对插入排序的优化,尽可能,先从全局的角度,把数据调整成区域有序,让全局的数据越来越有,即尽最快速度让数据变成趋于有序的,再统一进行一次插入排序。
实现思路
对数据进行分组插入排序
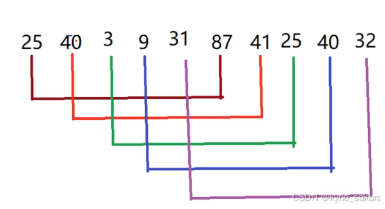
如下数组
int gap = size/2; //10/2 = 5
注意:gap的取值,可以根据实际数据情况来定。
将数据分成五组,对每个组内的数据进行插入排序。
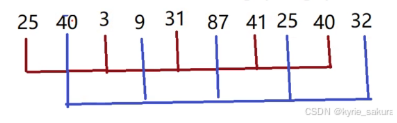
排序后
此时,数据并未有序,但相比较于这次比较前,整体数据更趋于有序。
gap进一步进行缩小。gap = gap/2; //5/2 = 2
此时的数据就变成下图的情况,分成了两组,对每组进行插入排序。
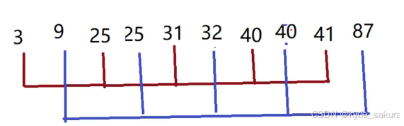
排序后:
gap进一步进行缩小。gap = gap/2; //2/2 = 1
此时,gap==1;对数据进行最后一遍插入排序。
代码实现
//希尔排序
void ShellSort(int arr[], int size)
{
for (int gap = size / 2; gap > 0; gap /= 2) //O(logn)
{
for (int i = gap; i < size; i++) //O(n)
{
int val = arr[i];
int j = i - gap;
for (; j >= 0; j-=gap) //O(n)
{
if (arr[j] <= val)
{
break;
}
arr[j + gap] = arr[j];
}
arr[j + gap] = val;
}
}
}
测试
int main()
{
int arr[10];
srand(time(NULL));
for (int i = 0; i < 10; i++)
{
arr[i] = rand() % 100 + 1;
}
for (int v : arr)
{
cout << v << " ";
}
cout << endl;
ShellSort(arr, sizeof(arr) / sizeof(arr[0]));
for (int v : arr)
{
cout << v << " ";
}
cout << endl;
return 0;
}
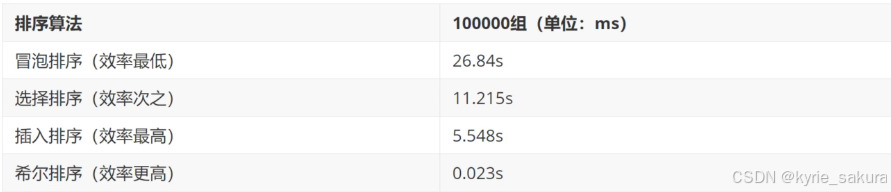
冒泡&选择&插入&希尔算法性能统计
代码实现
#include<iostream>
#include<stdlib.h> //包含随机数函数srand
#include<time.h> //需要用time作为随机数种子
#include<string>
#include<stack>
using namespace std;
//冒泡排序算法
void BubbleSort(int arr[], int size)
{
for (int i = 0; i < size; i++)//趟数
{
//一趟的处理
//进行优化,如果某趟没有进行如何的数据交换,那么说明数据已经有序
bool flag = false;
for (int j = 0; j < size - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = true;
}
}
if( !flag )
//if (flag = false)
{
//如果没有做任何的数据交换,那么说明数据已经有序了
return;
}
}
}
//选择排序算法
void ChoiceSort(int arr[], int size)
{
for (int i = 0; i < size-1; i++)
{
int min = arr[i];
int k = i;
for (int j = i+1; j < size; j++)
{
if (arr[j] < min)
{
min = arr[j];
k = j;
}
}
if (k != i)
{
int tmp = arr[i];
arr[i] = arr[k];
arr[k] = tmp;
}
}
}
//插入排序
//时间复杂度: 最坏、平均 O(n^2) 最好O(n) 空间:O(1) 稳定性:稳定的
void InsertSort(int arr[], int size)
{
for (int i = 1; i < size; i++)//O(n)
{
int val = arr[i];
int j = i - 1;
for (; j >= 0; j--) //O(n)
{
if (arr[j] <= val)
{
break;
}
arr[j + 1] = arr[j];
}
//val -> j+1
arr[j + 1] = val;
}
//这样产生了交换是不是插入排序
/*for (int i = 0; i < size - 1; i++)
{
for (int j = i; j >= 0; j--)
{
if (arr[j + 1] >= arr[j])
{
break;
}
else
{
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}*/
}
//希尔排序
void ShellSort(int arr[], int size)
{
for (int gap = size / 2; gap > 0; gap /= 2) //O(logn)
{
for (int i = gap; i < size; i++) //O(n)
{
int val = arr[i];
int j = i - gap;
for (; j >= 0; j-=gap) //O(n)
{
if (arr[j] <= val)
{
break;
}
arr[j + gap] = arr[j];
}
arr[j + gap] = val;
}
}
}
int main()
{
const int COUNT = 10000;
int* arr = new int[COUNT];
int* brr = new int[COUNT];
int* crr = new int[COUNT];
int* drr = new int[COUNT];
srand(time(NULL));
for (int i = 0; i < COUNT; i++)
{
int val = rand() % COUNT;
arr[i] = val;
brr[i] = val;
crr[i] = val;
drr[i] = val;
}
clock_t begin,end;
begin = clock();
BubbleSort(arr, COUNT);
end = clock();
cout << "BubbleSort spend: " << (end - begin) * 1.0 / CLOCKS_PER_SEC << "s" << endl;
begin = clock();
ChoiceSort(brr, COUNT);
end = clock();
cout << "ChoiceSort spend: " << (end - begin) * 1.0 / CLOCKS_PER_SEC << "s" << endl;
begin = clock();
InsertSort(crr, COUNT);
end = clock();
cout << "InsertSort spend: " << (end - begin) * 1.0 / CLOCKS_PER_SEC << "s" << endl;
begin = clock();
ShellSort(drr, COUNT);
end = clock();
cout << "ShellSort spend: " << (end - begin) * 1.0 / CLOCKS_PER_SEC << "s" << endl;
}
#if 0
int main()
{
int arr[10];
srand(time(NULL));
for (int i = 0; i < 10; i++)
{
arr[i] = rand() % 100 + 1;
}
for (int v : arr)
{
cout << v << " ";
}
cout << endl;
//BubbleSort(arr, sizeof(arr) / sizeof(arr[0]));
//ChoiceSort(arr, sizeof(arr) / sizeof(arr[0]));
//InsertSort(arr, sizeof(arr) / sizeof(arr[0]));
ShellSort(arr, sizeof(arr) / sizeof(arr[0]));
for (int v : arr)
{
cout << v << " ";
}
cout << endl;
return 0;
}
# endif
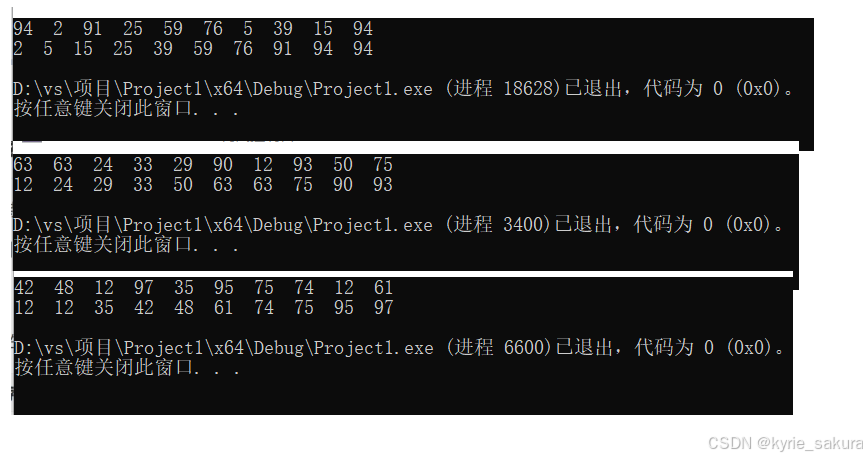
运行结果
数据量为10000时:
数据量为10w时: