前言

DBSCAN(Density-based spatial clustering of applicationswith noise)是Martin Ester, Hans-PeterKriegel等人于1996年提出的一种基于密度的聚类方法，聚类前不需要预先指定聚类的个数，生成的簇的个数不定（和数据有关)。该算法利用基于密度的聚类的概念，即要求聚类空间中的一定区域内所包含对象（点或其他空间对象）的数目不小于某一给定阈值。该方法能在具有噪声的空间数据库中发现任意形状的簇，可将密度足够大的相邻区域连接，能有效处理异常数据。

一、示例网站

DBSCAN可视化
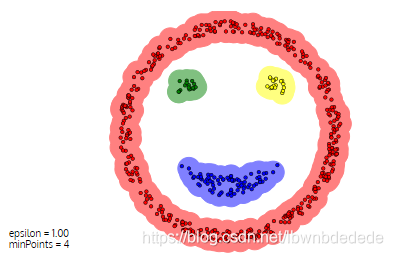
以“smile face”为例，K均值算法所示分类结果（四类，我随便确定的初始点）：

DBSCAN算法所示的分类结果：

显然后者的分类更加合理

二、DBSCAN数据点分类

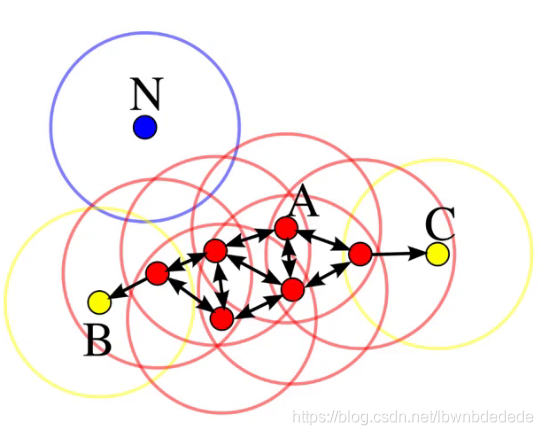
DBSCAN算法将数据点分为三类:
·核心点:在半径Eps内含有不少于MinPts数目的点
·边界点:在半径Eps内点的数量小于MinPts，但是落在核心点的邻域内
·噪音点:既不是核心点也不是边界点的点

在这幅图里，MinPts = 4，点A和其他红色点是核心点，因为它们的ε-邻域（图中红色圆圈)里包含最少4个点（包括自己)，由于它们之间相互相可达，它们形成了一个聚类。点B和点C不是核心点，但它们可由A经其他核心点可达，所以也和A属于同一个聚类。点N是局外点，它既不是核心点，又不由其他点可达。

三、伪代码

（来自维基百科）

四、DBSCAN的优缺点

优点:
1.基于密度定义，能处理任意形状和大小的簇;
2.可在聚类的同时发现异常点;
3.与K-means比较起来，不需要输入要划分的聚类个数。
缺点:
1.对输入参数é和Minpts敏感，确定参数困难;
2. 由于DBSCAN算法中，变量ε和Minpts是全局唯一的，当聚类的密度不均匀时，聚类距离相差很大时，聚类质量差;
3.当数据量大时，计算密度单元的计算复杂度大。