目标检测
文章目录
第1篇机器学习基础
1.标量、向量、矩阵、张量的概念及示例
当谈论线性代数时,我们经常会遇到以下几个基本概念:标量、向量、矩阵和张量。
- 标量(Scalar):标量是一个单独的数值,它没有方向和位置。在数学中,标量通常用小写字母表示,例如a、b、c等。标量可以是实数或复数。例如,温度、质量、时间等都是标量的例子。
- 向量(Vector):向量是由一组有序的数值组成,这些数值按照特定的顺序排列。向量具有大小和方向。在数学中,向量通常用小写粗体字母表示,例如v、w、x等。向量可以是二维、三维或更高维的。例如,位移、速度、力等都是向量的例子。
- 矩阵(Matrix):矩阵是一个二维数组,由一组数值按照行和列的方式排列组成。矩阵通常用大写字母表示,例如A、B、C等。矩阵的大小由它的行数和列数决定。例如,身高体重表、图像像素矩阵等都是矩阵的例子。
- 张量(Tensor):张量是一个多维数组,可以看作是向量和矩阵的推广。张量可以有任意多个维度,并且每个维度可以有任意多个元素。张量通常用大写粗体字母表示,例如T、U、V等。例如,彩色图像可以表示为三维张量,其中每个维度分别对应于宽度、高度和颜色通道。
示例:
- 标量:温度为30°C。
- 向量:速度为(5, -2, 0) m/s,表示在三个方向上的速度分量。
- 矩阵:矩阵A = [[1, 2, 3], [4, 5, 6]],表示一个2行3列的矩阵。
- 张量:三维张量T,其中T[i, j, k]表示在位置(i, j, k)处的数值。
2.机器学习的学习方式
机器学习是一种通过从数据中学习模式和规律来进行预测和决策的方法。它可以分为几种不同的学习方式,包括监督学习、无监督学习、半监督学习和强化学习。
2.1 监督学习
监督学习是一种通过使用带有标签的训练数据来训练模型,然后使用该模型进行预测的学习方式。在监督学习中,训练数据包含输入特征和对应的标签或输出。模型通过学习输入特征与标签之间的关系来进行预测。常见的监督学习算法包括:
- 线性回归:用于预测连续数值的算法,通过拟合一个线性函数来建立输入特征和输出之间的关系。
- 逻辑回归:用于分类问题的算法,通过拟合一个逻辑函数来建立输入特征和类别之间的关系。
- 决策树:通过构建一个树形结构来进行分类或回归预测。
- 支持向量机:通过找到一个最优的超平面来进行分类或回归预测。
- 随机森林:通过组合多个决策树来进行分类或回归预测。
2.2 无监督学习
无监督学习是一种从未标记的数据中发现模式和结构的学习方式。在无监督学习中,训练数据只包含输入特征,没有对应的标签或输出。模型通过学习数据的内在结构和相似性来进行聚类、降维等任务。常见的无监督学习算法包括:
- 聚类算法:将数据分成不同的组或簇,使得同一组内的数据相似度较高,不同组之间的相似度较低。
- 主成分分析(PCA):通过线性变换将高维数据映射到低维空间,以发现数据中的主要成分。
- 关联规则学习:发现数据中的频繁项集和关联规则,用于市场篮子分析等任务。
2.3 半监督学习
半监督学习是介于监督学习和无监督学习之间的学习方式。在半监督学习中,训练数据中既包含带有标签的数据,也包含未标记的数据。模型通过同时利用带标签数据和未标记数据来进行学习,以提高模型的性能和泛化能力。
2.4 强化学习
强化学习是一种通过与环境进行交互来学习最优行为策略的学习方式。在强化学习中,模型通过观察环境的状态,执行动作,并接收环境的奖励或惩罚来学习最优策略。强化学习常用于解决与序列决策相关的问题,如机器人控制、游戏策略等。常见的强化学习算法包括Q-learning、深度强化学习等。
3.机器学习分类和回归
3.1 常见分类算法对比
常见的分类算法包括决策树、随机森林、支持向量机(SVM)、朴素贝叶斯和K近邻(KNN)等。它们各有特点:
- 决策树:通过构建一个树形结构来进行分类,易于理解和解释,但容易过拟合。
- 随机森林:通过组合多个决策树来进行分类,具有较高的准确性和鲁棒性,能够处理大量特征,但模型较复杂。
- 支持向量机(SVM):通过找到一个最优的超平面来进行分类,适用于高维空间和非线性问题,但对大规模数据集和噪声敏感。
- 朴素贝叶斯:基于贝叶斯定理和特征之间的独立性假设,适用于文本分类和垃圾邮件过滤等问题,但对特征相关性较敏感。
- K近邻(KNN):通过计算样本之间的距离来进行分类,简单且易于实现,但对于高维数据和大规模数据集计算开销较大。
选择适合的分类算法取决于数据集的特征、问题的复杂性和性能要求等因素。
3.2 回归算法的分类
回归算法用于预测连续数值的输出,常见的回归算法可以分为线性回归、多项式回归、决策树回归、支持向量回归和神经网络回归等。
- 线性回归:通过拟合一个线性函数来建立输入特征和输出之间的关系。
- 多项式回归:通过引入多项式特征来拟合非线性关系。
- 决策树回归:通过构建一个树形结构来进行回归预测。
- 支持向量回归:通过找到一个最优的超平面来进行回归预测。
- 神经网络回归:通过神经网络模型来进行回归预测,可以处理复杂的非线性关系。
选择合适的回归算法取决于数据的特征、问题的复杂性和性能要求等因素。
3.3 逻辑回归适用性
逻辑回归适用于二分类问题,用于预测离散的输出变量,通常是0或1。它基于线性回归模型,通过将线性函数的输出映射到一个概率值(0到1之间),然后根据设定的阈值进行分类。
逻辑回归适用于以下情况:
- 二分类问题:逻辑回归可以用于解决二分类问题,如判断邮件是否为垃圾邮件、判断肿瘤是恶性还是良性等。
- 特征线性可分:逻辑回归假设特征与输出之间存在线性关系,因此适用于特征线性可分的问题。
- 数据量较小:逻辑回归对数据量的要求相对较低,适用于数据量较小的情况。
3.4 线性回归与逻辑回归的区别
线性回归和逻辑回归都属于回归算法,但它们在应用和特点上有一些区别:
- 输出类型:线性回归用于预测连续数值的输出,而逻辑回归用于预测离散的输出,通常是0或1。
- 模型形式:线性回归建立输入特征和输出之间的线性关系,逻辑回归通过将线性函数的输出映射到一个概率值,并进行分类。
- 适用性:线性回归适用于连续数值的预测问题,逻辑回归适用于二分类问题。
- 输出解释:线性回归的输出可以直接解释为预测值,逻辑回归的输出是一个概率值,需要根据设定的阈值进行分类。
3.5 机器学习分类回归术语表
- 特征(Feature):用于描述样本的属性或输入变量。
- 标签(Label):用于描述样本的输出变量或目标变量。
- 训练集(Training Set):用于训练模型的样本集合。
- 测试集(Test Set):用于评估模型性能的样本集合。
- 模型(Model):用于描述输入特征与输出之间的关系的数学函数或算法。
- 损失函数(Loss Function):用于衡量模型预测值与真实值之间的差异的函数。
- 优化算法(Optimization Algorithm):用于调整模型参数以最小化损失函数的算法。
- 过拟合(Overfitting):模型在训练集上表现良好,但在测试集上表现较差的现象。
- 欠拟合(Underfitting):模型无法很好地拟合训练集和测试集的现象。
- 泛化能力(Generalization Ability):模型对未见过的数据的适应能力。
- 正则化(Regularization):用于减小模型复杂度,防止过拟合的技术。
- 超参数(Hyperparameter):在模型训练之前需要手动设置的参数,如学习率、正则化系数等。
这些术语在机器学习中经常被使用,了解它们的含义可以帮助更好地理解和应用机器学习算法。
4.损失函数
4.1 什么是损失函数
损失函数(Loss Function)是机器学习中用于衡量模型预测值与真实值之间差异的函数。它是模型优化的目标函数,用于评估模型的性能和指导参数的更新。
4.2 损失函数的作用
损失函数的作用是衡量模型预测值与真实值之间的差异,通过最小化损失函数来调整模型的参数,使模型能够更好地拟合训练数据,并具有更好的泛化能力。
4.3 常用的损失函数
4.3.1 0-1损失函数(Zero-One Loss): 0-1损失函数是一种简单的分类损失函数,当模型的预测值与真实值不一致时,损失为1,否则为0。这种损失函数在实际应用中很少使用,因为它不可导且不连续。
4.3.2 绝对值损失函数(Absolute Loss): 绝对值损失函数是回归问题中常用的损失函数,它衡量模型预测值与真实值之间的绝对差异。它对异常值比较敏感,但具有较好的鲁棒性。
4.3.3 平方损失函数(Squared Loss): 平方损失函数是回归问题中最常用的损失函数之一,它衡量模型预测值与真实值之间的平方差异。平方损失函数对异常值敏感,但在数学计算和优化过程中具有良好的性质。
4.3.4 对数损失函数(Logarithmic Loss): 对数损失函数常用于二分类问题和多分类问题中,它衡量模型预测值与真实值之间的对数差异。对数损失函数越小,表示模型的预测结果越接近真实值。
4.3.5 交叉熵损失函数(Cross-Entropy Loss): 交叉熵损失函数常用于分类问题中,特别是多分类问题。它衡量模型预测值与真实值之间的交叉熵差异。交叉熵损失函数在训练过程中能够更好地引导模型的学习。
4.3.6 指数损失函数(Exponential Loss): 指数损失函数常用于二分类问题中,它衡量模型预测值与真实值之间的指数差异。指数损失函数对异常值敏感,但在一些特定的问题中具有较好的性能。
4.3.7 L1 Loss: L1 Loss是绝对值损失函数的另一种称呼,它衡量模型预测值与真实值之间的绝对差异。L1 Loss在回归问题中常用于稀疏解的求解。
4.3.8 L2损失函数(LSE): L2损失函数是平方损失函数的另一种称呼,它衡量模型预测值与真实值之间的平方差异。L2损失函数在回归问题中广泛使用,具有良好的数学性质。
4.3.9 均方差损失函数(MSE): 均方差损失函数是平方损失函数的一种特殊形式,它衡量模型预测值与真实值之间的平方差异的平均值。均方差损失函数在回归问题中常用于衡量模型的拟合程度。
4.3.10 平均绝对误差(MAE): 平均绝对误差是绝对值损失函数的一种特殊形式,它衡量模型预测值与真实值之间的绝对差异的平均值。平均绝对误差在回归问题中常用于评估模型的性能。
这些损失函数在不同的问题和任务中具有不同的适用性和性质,选择合适的损失函数对于模型的训练和优化非常重要。
5.随机梯度下降
5.1 什么是梯度下降
梯度下降(Gradient Descent)是一种常用的优化算法,用于最小化损失函数或目标函数。它通过迭代更新模型参数,使损失函数的值逐渐减小,从而找到最优解。
在梯度下降中,首先计算损失函数对于每个参数的梯度(即导数),然后按照梯度的方向和大小来更新参数。梯度的方向指向损失函数上升最快的方向,因此通过朝着梯度的反方向更新参数,可以逐步接近损失函数的最小值。
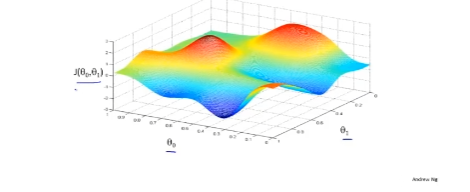
存在函数 J ( Θ 0 , Θ 1 ) J(\Theta_0, \Theta_1) J(Θ0,Θ1)
想得到 min Θ 0 Θ 1 J ( Θ 0 , Θ 1 ) \mathop{\min}\limits_{\Theta_0\Theta_1}J(\Theta_0, \Theta_1) Θ0Θ1minJ(Θ0,Θ1)
define:
Θ j : = Θ j − α ∂ ∂ Θ j J ( Θ 0 , Θ 1 ) \Theta_j:=\Theta_j-\alpha \frac{\partial}{\partial\Theta_j}J(\Theta_0,\Theta_1) Θj:=Θj−α∂Θj∂J(Θ0,Θ1) ( f o r j = 0 a n d j = 1 ) (for\space j\space =\space 0\space and\space j =\space 1) (for j = 0 and j= 1)
: = := :=表示赋值
α \alpha α表示梯度下降时,迈出多大的步子(学习速率)
∂ ∂ Θ j J ( Θ 0 , Θ 1 ) \frac{\partial}{\partial\Theta_j}J(\Theta_0,\Theta_1) ∂Θj∂J(Θ0,Θ1)是一个导数项
需要同时更新 Θ 0 , Θ 1 \Theta_0,\Theta_1 Θ0,Θ1
t e m p 0 : = Θ 0 − α ∂ ∂ Θ j J ( Θ 0 , Θ 1 ) temp0:=\Theta_0-\alpha \frac{\partial}{\partial\Theta_j}J(\Theta_0,\Theta_1) temp0:=Θ0−α∂Θj∂J(Θ0,Θ1)
t e m p 1 : = Θ 1 − α ∂ ∂ Θ j J ( Θ 0 , Θ 1 ) temp1:=\Theta_1-\alpha \frac{\partial}{\partial\Theta_j}J(\Theta_0,\Theta_1) temp1:=Θ1−α∂Θj∂J(Θ0,Θ1)
Θ 0 : = t e m p 0 \Theta_0:=temp0 Θ0:=temp0
Θ 1 : = t e m p 1 \Theta_1:=temp1 Θ1:=temp1
∂ ∂ Θ j J ( Θ 0 , Θ 1 ) = ∂ ∂ θ j ∙ 1 2 m ∑ ( h Θ ( x ) − y ) 2 \frac{\partial}{\partial\Theta_j}J(\Theta_0,\Theta_1)=\frac{\partial}{\partial \theta_j}\bullet \frac{1}{2m}\sum(h_\Theta(x)-y)^2 ∂Θj∂J(Θ0,Θ1)=∂θj∂∙2m1∑(hΘ(x)−y)2
= ∂ ∂ θ j ∙ 1 2 m ∑ ( θ 0 + θ 1 x ( i ) − y ( i ) ) 2 =\frac{\partial}{\partial \theta_j}\bullet \frac{1}{2m}\sum(\theta_0+\theta_1x^{(i)}-y^{(i)})^2 =∂θj∂∙2m1∑(θ0+θ1x(i)−y(i))2
j = 0 : ∂ ∂ Θ j J ( Θ 0 , Θ 1 ) = 1 m ∑ ( h ( x ( i ) ) − y ( i ) ) j = 0 : \frac{\partial}{\partial\Theta_j}J(\Theta_0,\Theta_1)=\frac{1}{m}\sum(h(x^{(i)})-y^{(i)}) j=0:∂Θj∂J(Θ0,Θ1)=m1∑(h(x(i))−y(i))
j = 1 : ∂ ∂ Θ j J ( Θ 0 , Θ 1 ) = 1 m ∑ ( h ( x ( i ) ) − y ( i ) ) ∙ x ( i ) j = 1 : \frac{\partial}{\partial\Theta_j}J(\Theta_0,\Theta_1)=\frac{1}{m}\sum(h(x^{(i)})-y^{(i)})\bullet x^{(i)} j=1:∂Θj∂J(Θ0,Θ1)=m1∑(h(x(i))−y(i))∙x(i)
code
import numpy as np
# 定义梯度下降的线性回归模型类
class LinearRegression:
def __init__(self, learning_rate=0.01, num_iters=1000):
self.learning_rate = learning_rate # 学习率
self.num_iters = num_iters # 迭代次数
self.weights = None # 线性回归的权重
self.bias = None # 线性回归的偏差
def fit(self, X, y):
num_samples, num_features = X.shape
# 初始化权重和偏差为0
self.weights = np.zeros(num_features)
self.bias = 0
# 梯度下降迭代
for _ in range(self.num_iters):
# 计算线性关系预测值
y_pred = np.dot(X, self.weights) + self.bias
# 计算误差
error = y_pred - y
# 计算梯度
dw = (1 / num_samples) * np.dot(X.T, error)
db = (1 / num_samples) * np.sum(error)
# 更新权重和偏差
self.weights -= self.learning_rate * dw
self.bias -= self.learning_rate * db
def predict(self, X):
# 使用训练得到的权重和偏差进行预测
y_pred = np.dot(X, self.weights) + self.bias
return y_pred
# 测试例子
X = np.array([[1], # 样本1
[2], # 样本2
[4], # 样本3
[3], # 样本4
[5]]) # 样本5
y = np.array([3, 4, 6, 5, 7]) # 目标变量
# 创建线性回归模型对象
model = LinearRegression(learning_rate=0.01, num_iters=1000)
# 拟合数据
model.fit(X, y)
# 进行预测
X_test = np.array([[2], [6]])
predictions = model.predict(X_test)
print("预测结果:", predictions)
特征数据 X 为一维,因为这里只有一个特征 x。对应的目标变量 y 也为一维。
在这个例子中,我们通过 X 和 y 定义了线性回归的训练数据。然后,我们创建了一个模型对象 model,并使用 fit 函数拟合数据。最后,通过 predict 函数进行预测。
需要注意的是,这只是一个简单的线性回归模型实现示例,在实际应用中,可能需要考虑更多的特征和复杂性,以获得更准确的预测结果。
5.2 梯度下降的优缺点
梯度下降的优点包括:
- 简单易实现:梯度下降算法相对简单,易于实现和理解。
- 广泛适用:梯度下降可以应用于各种机器学习算法和模型优化问题。
- 可扩展性:梯度下降可以处理大规模数据集和高维参数空间。
梯度下降的缺点包括:
- 可能陷入局部最优解:梯度下降可能会陷入局部最优解,而无法达到全局最优解。
- 学习率选择困难:梯度下降的性能受到学习率的影响,选择合适的学习率是一个挑战。
- 可能收敛速度慢:梯度下降可能需要较长的时间才能收敛到最优解。
5.3 梯度下降的变种
梯度下降有多种变种,其中常见的包括:
- 批量梯度下降(Batch Gradient Descent):在每次迭代中使用全部训练样本来计算梯度和更新参数。
- 随机梯度下降(Stochastic Gradient Descent):在每次迭代中使用单个训练样本来计算梯度和更新参数。
- 小批量梯度下降(Mini-Batch Gradient Descent):在每次迭代中使用一小批训练样本来计算梯度和更新参数。
这些变种在计算效率、收敛速度和稳定性等方面有所不同,可以根据具体问题和数据集的特点选择合适的变种。
5.4 各种梯度下降法性能比较
不同的梯度下降变种在性能上有所差异,具体的性能比较取决于问题的特点和数据集的规模。一般来说:
- 批量梯度下降通常具有较好的收敛性,但计算开销较大,特别是在大规模数据集上。
- 随机梯度下降具有较快的收敛速度,但可能会更不稳定,因为每次迭代只使用一个样本计算梯度。
- 小批量梯度下降折中了批量梯度下降和随机梯度下降的优点,通常具有较好的收敛速度和计算效率。
6.模型评估
6.1 模型评估常用方法
常用的模型评估方法包括:
- 准确率(Accuracy):模型预测正确的样本数占总样本数的比例。
- 精确率(Precision):预测为正例的样本中真正为正例的比例。
- 召回率(Recall):真正为正例的样本中被预测为正例的比例。
- F1值(F1-Score):精确率和召回率的调和平均值,综合考虑了两者的性能。
- ROC曲线(Receiver Operating Characteristic Curve):以真正例率(True Positive Rate)为纵轴,假正例率(False Positive Rate)为横轴绘制的曲线,用于评估二分类模型的性能。
- PR曲线(Precision-Recall Curve):以精确率为纵轴,召回率为横轴绘制的曲线,用于评估二分类模型的性能。
- 混淆矩阵(Confusion Matrix):用于展示分类模型预测结果的正确和错误情况,包括真正例、假正例、真反例和假反例。
6.2 误差、偏差和方差
- 误差(Error):模型预测值与真实值之间的差异。
- 偏差(Bias):模型预测值的平均偏离真实值的程度,衡量了模型的拟合能力。
- 方差(Variance):模型预测值的变化范围,衡量了模型的稳定性和泛化能力。
6.3 经验误差与泛化误差
- 经验误差(Empirical Error):模型在训练集上的误差,衡量了模型在已知数据上的拟合程度。
- 泛化误差(Generalization Error):模型在未知数据上的误差,衡量了模型在新数据上的预测能力。
6.4 过拟合与欠拟合
-
过拟合(Overfitting):模型在训练集上表现良好,但在测试集上表现较差,泛化能力较差。
-
欠拟合(Underfitting):模型无法很好地拟合训练集和测试集,无法捕捉数据中的模式和规律。
-
过拟合解决方法:
- 增加训练数据量。
- 减少模型复杂度,如减少参数数量或降低模型的层数。
- 使用正则化技术,如L1正则化、L2正则化等。
- 采用集成学习方法,如随机森林、梯度提升树等。
-
欠拟合解决方法:
- 增加模型复杂度,如增加参数数量或增加模型的层数。
- 使用更复杂的模型,如深度神经网络等。
- 增加特征数量或改进特征工程。
- 减少正则化程度。
6.5 交叉验证
交叉验证是一种模型评估的方法,主要用于评估模型的泛化能力和选择合适的超参数。它将数据集划分为训练集和验证集,通过多次训练和验证来评估模型在不同数据子集上的性能,从而更好地估计模型在未知数据上的表现。
6.6 错误率及精度
- 错误率(Error Rate):模型预测错误的样本数占总样本数的比例。
- 精度(Accuracy):模型预测正确的样本数占总样本数的比例。
6.7 查准率与查全率
- 查准率(Precision):预测为正例的样本中真正为正例的比例。
- 查全率(Recall):真正为正例的样本中被预测为正例的比例。
6.8 比较检验方法
常见的模型比较检验方法包括:
- t检验(t-test):用于比较两个样本均值是否有显著差异。
- 方差分析(ANOVA):用于比较多个样本均值是否有显著差异。
- 卡方检验(Chi-square test):用于比较两个或多个分类变量之间的关联性。
- McNemar检验:用于比较两个配对样本的分类结果是否有显著差异。
- Wilcoxon符号秩检验(Wilcoxon signed-rank test):用于比较两个配对样本的中位数是否有显著差异。
- Friedman检验:用于比较多个配对样本的中位数是否有显著差异。
6.9 类别不平衡
类别不平衡指的是在分类问题中,不同类别的样本数量差异较大。类别不平衡问题可能由以下原因引起:
- 样本采集偏差:数据采集过程中对不同类别样本的采集方式存在偏差。
- 样本分布不均匀:真实世界中某些类别的样本数量本来就较少。
- 样本标注错误:样本标注过程中对不同类别的判断存在错误。
常见的类别不平衡问题解决方法包括:
- 重采样(Resampling):通过欠采样或过采样调整样本分布,使不同类别的样本数量更加平衡。
- 类别权重调整(Class Weighting):通过调整不同类别的权重,使模型更关注少数类别的样本。
- 阈值调整(Threshold Adjustment):通过调整分类阈值来平衡不同类别的预测结果。
- 生成合成样本(Synthetic Sample Generation):通过生成合成样本来增加少数类别的样本数量。
- 集成学习(Ensemble Learning):通过组合多个模型的预测结果来提高少数类别的预测性能。
6.10 评价指标选择案例
选择合适的评价指标取决于具体的问题和任务。以下是一些常见的评价指标选择案例:
- 对于二分类问题,可以使用准确率、精确率、召回率、F1值、ROC曲线和PR曲线等指标。
- 对于多分类问题,可以使用准确率、混淆矩阵、多分类的精确率和召回率等指标。
- 对于回归问题,可以使用均方差(MSE)、平均绝对误差(MAE)等指标。
- 对于异常检测问题,可以使用精确率、召回率、F1值等指标。
第2篇深度学习基础
基本概念
深度学习是一种机器学习方法,通过构建和训练深层神经网络来实现对数据的学习和预测。深度学习的核心思想是通过多层非线性变换来提取数据的高级特征,并使用这些特征进行模式识别和预测。
1.前向传播与反向传播
1.1 前向传播
前向传播是指从输入层到输出层的信号传递过程。在前向传播过程中,输入数据经过一系列的线性和非线性变换,最终得到模型的预测结果。
1.2 反向传播
反向传播是指从输出层到输入层的误差反向传递过程。在反向传播过程中,通过计算损失函数对模型参数的梯度,将误差从输出层逐层向后传播,更新模型参数以最小化损失函数。
2.超参数
2.1 什么是超参数
超参数是在模型训练之前需要手动设置的参数,不同于模型参数,超参数的值不能通过训练数据自动学习得到。
2.2 超参数如何影响模型性能
超参数的选择会直接影响模型的性能和泛化能力。不同的超参数值可能导致模型的拟合能力、稳定性和收敛速度等方面的差异。
2.3 为什么要进行超参数调优
超参数调优是为了找到最优的超参数组合,以提高模型的性能和泛化能力。通过调整超参数,可以改善模型的拟合能力、减少过拟合或欠拟合等问题。
2.4 如何寻找超参数的最优值
寻找超参数的最优值可以通过网格搜索、随机搜索、贝叶斯优化等方法。这些方法可以在给定的超参数空间中进行搜索,并根据评估指标选择最佳的超参数组合。
2.5 超参数搜索一般过程
超参数搜索的一般过程包括:
- 定义超参数空间:确定需要调优的超参数以及其取值范围。
- 选择搜索方法:选择合适的搜索方法,如网格搜索、随机搜索或贝叶斯优化。 定义评估指标:选择适当的评估指标来衡量模型性能。
- 进行搜索:在超参数空间中进行搜索,并根据评估指标选择最佳的超参数组合。
- 评估模型:使用最佳的超参数组合训练模型,并在测试集上评估模型的性能。
- 调整超参数:根据评估结果调整超参数的取值范围,并重新进行搜索和评估,直到找到最优的超参数组合。
3.激活函数
3.1 激活函数的概念
激活函数是神经网络中的一种非线性函数,它将输入信号转换为输出信号。在神经网络的每个神经元中,激活函数决定了神经元是否应该被激活并传递信号给下一层。
3.2 为什么要引入激活函数
引入激活函数的主要原因是为了给神经网络引入非线性特性。如果没有激活函数,多层神经网络将只能表示线性关系,无法学习复杂的非线性模式。激活函数的引入使得神经网络能够学习和表示更加复杂的函数关系。
3.3 为什么激活函数是非线性函数
激活函数需要是非线性函数,因为线性函数的组合仍然是线性的。如果激活函数是线性的,多层神经网络的输出将仍然是输入的线性组合,无法学习和表示非线性模式。非线性激活函数的引入使得神经网络能够学习和表示非线性模式。
3.4 常见的激活函数 常见的激活函数包括:
- Sigmoid函数:将输入映射到0到1之间的连续值。
- Tanh函数:将输入映射到-1到1之间的连续值。
- ReLU函数:将负值映射为0,正值保持不变。
- Leaky ReLU函数:在负值区域引入一个小的斜率,以解决ReLU函数的死亡神经元问题。
- Softmax函数:将多个输入映射到0到1之间的概率分布。
3.5 激活函数性质 激活函数应具备以下性质:
- 非线性:能够引入非线性特性。
- 可微分:能够计算梯度以进行反向传播。
- 单调性:能够保持输入的相对大小关系。
- 饱和性:能够限制输出值的范围,避免梯度消失或爆炸。
3.6 如何选择激活函数? 选择激活函数需要考虑问题的性质和网络的结构。一般来说,ReLU是常用的默认选择,因为它在实践中表现良好并且计算效率高。但对于某些问题,如处理负值较多的数据,可以考虑使用其他激活函数,如Tanh或Leaky ReLU。此外,对于多分类问题,可以使用Softmax作为输出层的激活函数。
4.BatchSize
4.1 Epoch、Iteration和BatchSize的关系
在训练神经网络时,数据集通常被分成多个批次进行训练。一个Epoch表示将所有的训练样本都过一遍的训练过程。一个Iteration表示在一个Epoch中进行一次前向传播和反向传播的过程。BatchSize表示每个批次中包含的样本数量。
4.2 BatchSize的选择
选择合适的BatchSize需要考虑计算资源和模型性能之间的平衡。较大的BatchSize可以提高计算效率,但可能会导致模型过拟合。较小的BatchSize可以提高模型的泛化能力,但可能会增加计算时间。
4.3 BatchSize是否越大越好
BatchSize的大小并没有绝对的规定,取决于具体的问题和数据集。较大的BatchSize可以加快训练速度,但可能会导致模型过拟合。较小的BatchSize可以提高模型的泛化能力,但可能会增加计算时间。因此,需要根据具体情况进行选择。
5.归一化
5.1 为什么要归一化
归一化是为了将不同特征的取值范围统一到相同的尺度上。这样做的好处是可以加快模型的收敛速度,提高模型的稳定性,并且可以避免某些特征对模型训练的影响过大。
5.2 为什么归一化能提高求解最优解速度
归一化能提高求解最优解的速度是因为归一化后,各个特征的取值范围相同,使得模型在更新参数时能够更快地找到最优解。如果不进行归一化,不同特征的取值范围差异较大,可能导致模型在更新参数时受到某些特征的影响过大,从而导致收敛速度变慢。
5.3 常用归一化方式
常用的归一化方式包括:
- 最大最小归一化(Min-Max Normalization):将特征缩放到一个指定的最小值和最大值之间。
- Z-score归一化:将特征缩放为均值为0,标准差为1的分布。
- 小数定标归一化(Decimal Scaling):将特征缩放为[-1, 1]之间的范围。
5.4 局部响应归一化(Local Response Normalization,LRN)
局部响应归一化是一种在卷积神经网络中常用的归一化方式。它通过对每个神经元的输出进行归一化,使得神经元的响应对于相邻神经元的响应不敏感。
5.5 批归一化(Batch Normalization,BN)
批归一化是一种在神经网络中常用的归一化方式。它通过对每个批次的输入进行归一化,使得神经网络在训练过程中更加稳定,加快收敛速度,并且可以使用较大的学习率。
5.6 Batch Normalization算法流程
Batch Normalization的算法流程如下:
- 对每个批次的输入进行归一化,使得均值为0,方差为1。
- 对归一化后的数据进行线性变换和平移,恢复数据的均值和方差。
- 将变换后的数据作为下一层的输入。
5.7 群组归一化(Group Normalization,GN)
群组归一化是一种在神经网络中常用的归一化方式。它将特征分成多个组,对每个组进行归一化,使得神经网络在训练过程中更加稳定,加快收敛速度。
5.8 权重归一化(Weight Normalization,WN)
权重归一化是一种在神经网络中常用的归一化方式。它通过对权重进行归一化,使得神经网络在训练过程中更加稳定,加快收敛速度。
5.9 批归一化在网络中的位置
批归一化通常在卷积层或全连接层之后、激活函数之前进行。它可以作为网络的一部分,也可以作为独立的层来使用。
6.预训练与微调(fine tuning)
6.1 特征提取和模型微调
特征提取是指使用预训练的模型,将其前面的层固定住,只训练后面的全连接层或分类器层,以提取输入数据的特征。模型微调是指使用预训练的模型作为初始权重,在新的任务上进行训练,包括调整模型的所有层的权重。
6.2 微调和直接训练有什么不同
微调和直接训练的不同之处在于初始权重的选择。微调使用预训练的模型作为初始权重,而直接训练则从头开始随机初始化权重。微调可以利用预训练模型在大规模数据上学到的特征,加速模型在新任务上的收敛速度。
6.3 微调模型的三种方式
微调模型有三种方式:
- 冻结:固定预训练模型的所有层的权重,只训练新添加的层。
- 部分冻结:固定预训练模型的部分层的权重,只训练剩余的层。
- 全部微调:训练整个模型的所有层的权重。
6.4 实际应用中的微调方法 在实际应用中,微调方法可以根据具体任务和数据集的特点进行选择。如果数据集与预训练模型的数据集相似,可以尝试冻结一部分层并微调剩余的层。如果数据集与预训练模型的数据集差异较大,可以尝试全部微调或从头开始训练。
7.初始化
7.1 全零初始化
全零初始化是一种简单的权重初始化方法,将所有权重初始化为0。但全零初始化会导致模型对称性问题,使得每个神经元的输出都相同,无法进行有效的学习。
7.2 随机初始化
随机初始化是一种常用的权重初始化方法,将权重初始化为随机的小值。随机初始化可以打破对称性,使得每个神经元的输出具有差异性,有利于模型的学习。
7.3 Xavier初始化
Xavier初始化是一种常用的权重初始化方法,根据输入和输出的维度来确定权重的初始化范围。Xavier初始化可以使得每个神经元的输出具有相同的方差,有利于模型的学习。
7.4 He初始化
He初始化是一种常用的权重初始化方法,根据输入的维度来确定权重的初始化范围。He初始化可以使得每个神经元的输出具有相同的方差,适用于使用ReLU激活函数的模型。
7.5 偏差初始化
偏差初始化是一种常用的初始化方法,将偏差初始化为0或者一个较小的常数。偏差初始化可以使得模型在初始阶段更容易学习到偏差的影响,有利于模型的学习。
7.6 初始化方式小结
权重初始化是神经网络训练的重要步骤,不同的初始化方式适用于不同的模型和激活函数。随机初始化、Xavier初始化和He初始化是常用的权重初始化方法,可以根据具体情况选择合适的初始化方式。偏差初始化可以使得模型更容易学习到偏差的影响。
8.学习率
8.1 学习率的作用
学习率是神经网络训练中的一个重要超参数,它决定了每次参数更新的步长。学习率的大小直接影响模型的收敛速度和最终的性能。较大的学习率可以加快收敛速度,但可能会导致模型在最优解附近震荡或发散;较小的学习率可以提高模型的稳定性,但可能会导致收敛速度较慢。
8.2 常见学习率衰减参数
常见的学习率衰减参数包括:
- 初始学习率(Initial Learning Rate):训练开始时的学习率。
- 学习率衰减因子(Learning Rate Decay Factor):用于控制学习率的衰减速度。
- 学习率衰减周期(Learning Rate Decay Period):学习率衰减的周期,即在多少个Epoch或Iteration后进行一次衰减。
8.3 常见学习率衰减方法
常见的学习率衰减方法包括:
- 固定衰减(Fixed Decay):在训练的每个周期或一定的迭代次数后,将学习率按照固定的衰减因子进行衰减。
- 周期性衰减(Periodic Decay):在训练的每个周期或一定的迭代次数后,将学习率按照固定的衰减因子进行衰减,并重置为初始学习率。
- 指数衰减(Exponential Decay):根据指数函数衰减学习率,学习率衰减因子决定衰减的速度。
- 余弦退火(Cosine Annealing):根据余弦函数的形状衰减学习率,学习率衰减周期决定衰减的频率。
- 自适应调整(Adaptive Adjustments):根据模型的性能和训练过程中的动态变化,自适应地调整学习率。
9.正则化
9.1 为什么要正则化
正则化是一种用于减少模型过拟合的技术。在训练神经网络时,模型可能会过度拟合训练数据,导致在新数据上的泛化能力较差。正则化通过对模型的参数进行约束,可以降低模型的复杂度,提高模型的泛化能力。
9.2 为什么正则化能减少过拟合
正则化能减少过拟合的原因有两个方面:
- 参数惩罚:正则化通过对模型的参数进行惩罚,限制参数的取值范围,使得模型的复杂度降低。这样可以减少模型对训练数据的过度拟合,提高模型在新数据上的泛化能力。
- 特征选择:正则化可以通过对模型的参数进行约束,使得某些参数的取值趋近于0,从而实现特征选择的效果。这样可以减少模型对无关特征的依赖,提高模型的泛化能力。
9.3 Dropout正则化
Dropout是一种常用的正则化技术,它在训练过程中随机地将一部分神经元的输出置为0,以降低神经元之间的依赖关系。Dropout可以减少模型对某些特定神经元的依赖,从而提高模型的泛化能力。在测试阶段,Dropout会关闭,所有神经元的输出都会被保留,但会乘以一个与训练时Dropout概率相等的因子,以保持输出的期望值不变。
Dropout的一个缺点是在训练过程中,每个样本的前向传播和反向传播都需要重新计算,导致训练时间增加。此外,Dropout可能会导致模型的输出具有随机性,使得模型的解释性降低。因此,在使用Dropout时需要权衡模型的性能和计算资源的消耗。
第3篇卷积神经网络
1.卷积神经网络发展
1.1传统的图像处理方法
传统的图像处理方法主要包括图像增强、图像分割、图像特征提取和图像分类等。这些方法通常使用手工设计的特征,如颜色、纹理、形状等,来表示图像。
1.2深度学习的图像处理方法
深度学习的图像处理方法主要包括卷积神经网络(CNN)、循环神经网络(RNN)和生成对抗网络(GAN)等。这些方法使用数据驱动的学习方式,从数据中自动学习图像的特征,从而实现图像处理任务。
2.卷积和卷积核
卷积层是卷积神经网络(CNN)的核心组成部分。它使用一组卷积核在输入数据上进行卷积运算,从而提取输入数据中的特征。卷积层的计算过程如下:
- 输入数据:卷积层接收一个三维输入数据,形状为 (H, W, C),其中 H 和 W 是输入数据的高度和宽度,C 是输入数据的通道数。
- 卷积核:卷积层使用一组卷积核,形状为 (h, w, C),其中 h 和 w 是卷积核的高度和宽度,C 是卷积核的通道数。卷积核的通道数必须与输入数据的通道数相同。
- 卷积运算:卷积层对输入数据和卷积核进行卷积运算。卷积运算的具体过程如下:
- 将卷积核在输入数据上滑动,每次滑动一个像素。
- 在每个滑动位置,将卷积核与输入数据在该位置的局部区域进行元素积。
- 将元素积的结果求和,得到一个标量值。
- 激活函数:卷积运算的结果通常通过一个激活函数进行非线性变换。常用的激活函数包括 ReLU、Sigmoid 和 Tanh。
- 输出特征图:卷积层输出一个三维特征图,形状为 (H’, W’, C’),其中 H’ 和 W’ 是输出特征图的高度和宽度,C’ 是输出特征图的通道数。输出特征图的通道数等于卷积核的个数。
卷积层的计算过程可以表示为:
复制代码F(x) = f(W * x + b)
其中:
- F(x) 是卷积层的输出特征图。
- x 是卷积层的输入数据。
- W 是卷积层的卷积核。
- b 是卷积层的偏置项。
- f 是卷积层的激活函数。
卷积层可以提取输入数据中的局部特征。卷积核的大小和数量可以根据具体任务进行调整。卷积层是 CNN 中非常重要的一个组成部分,它在图像分类、目标检测、图像分割等任务中都有着广泛的应用。
例如,让我们找到图像“A”的轮廓(边缘)。
Android A 我们可以使用以下的卷积核或权重集。
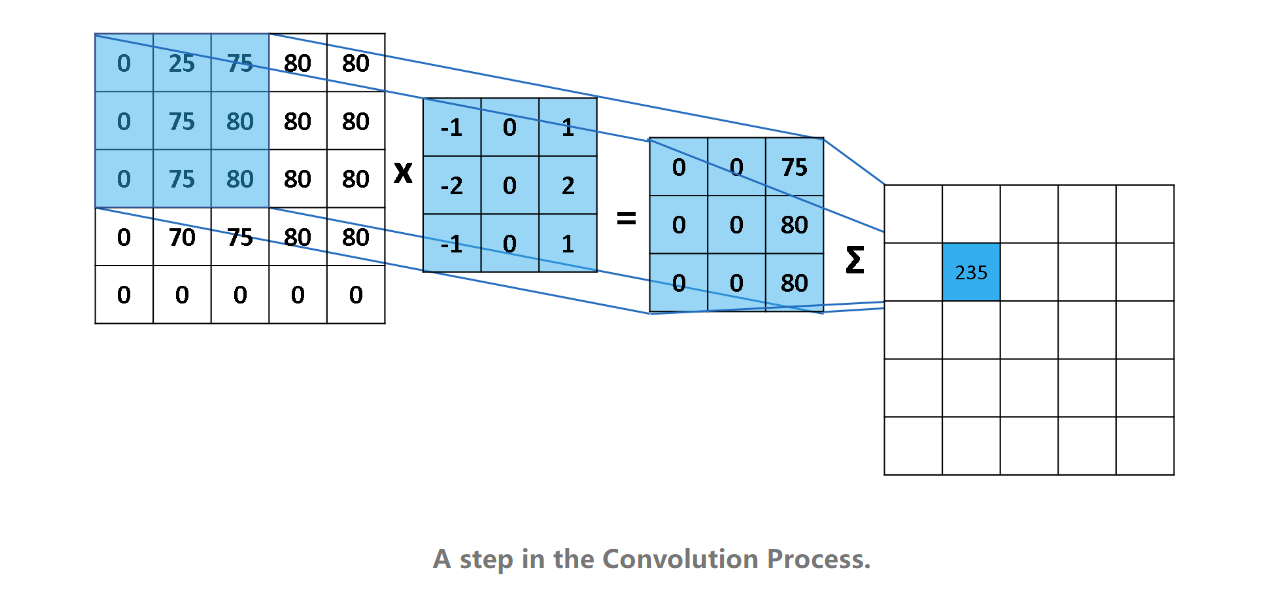
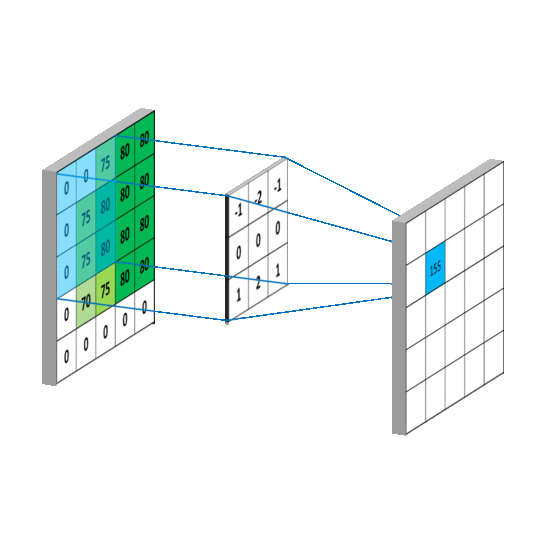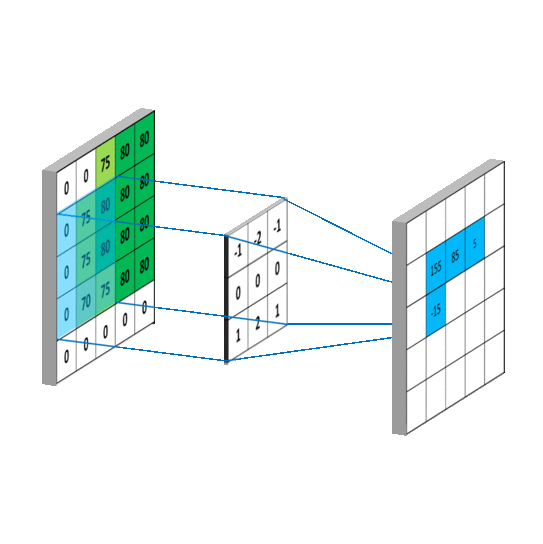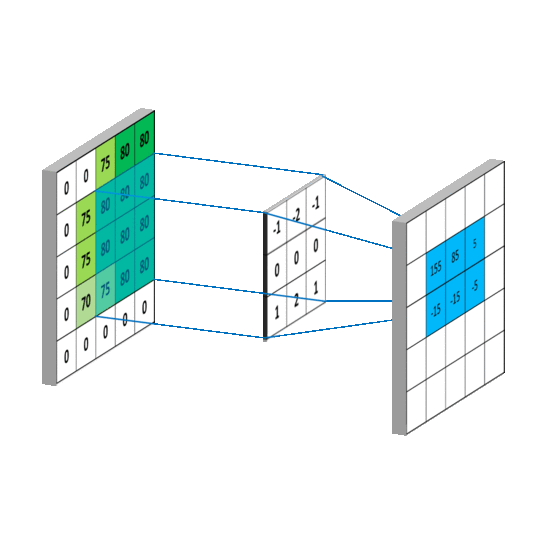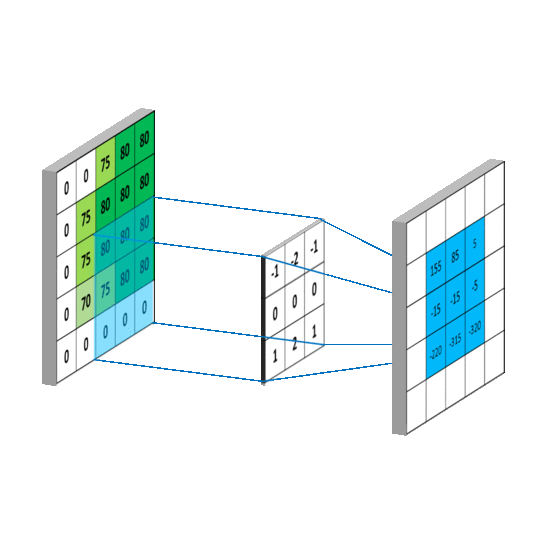
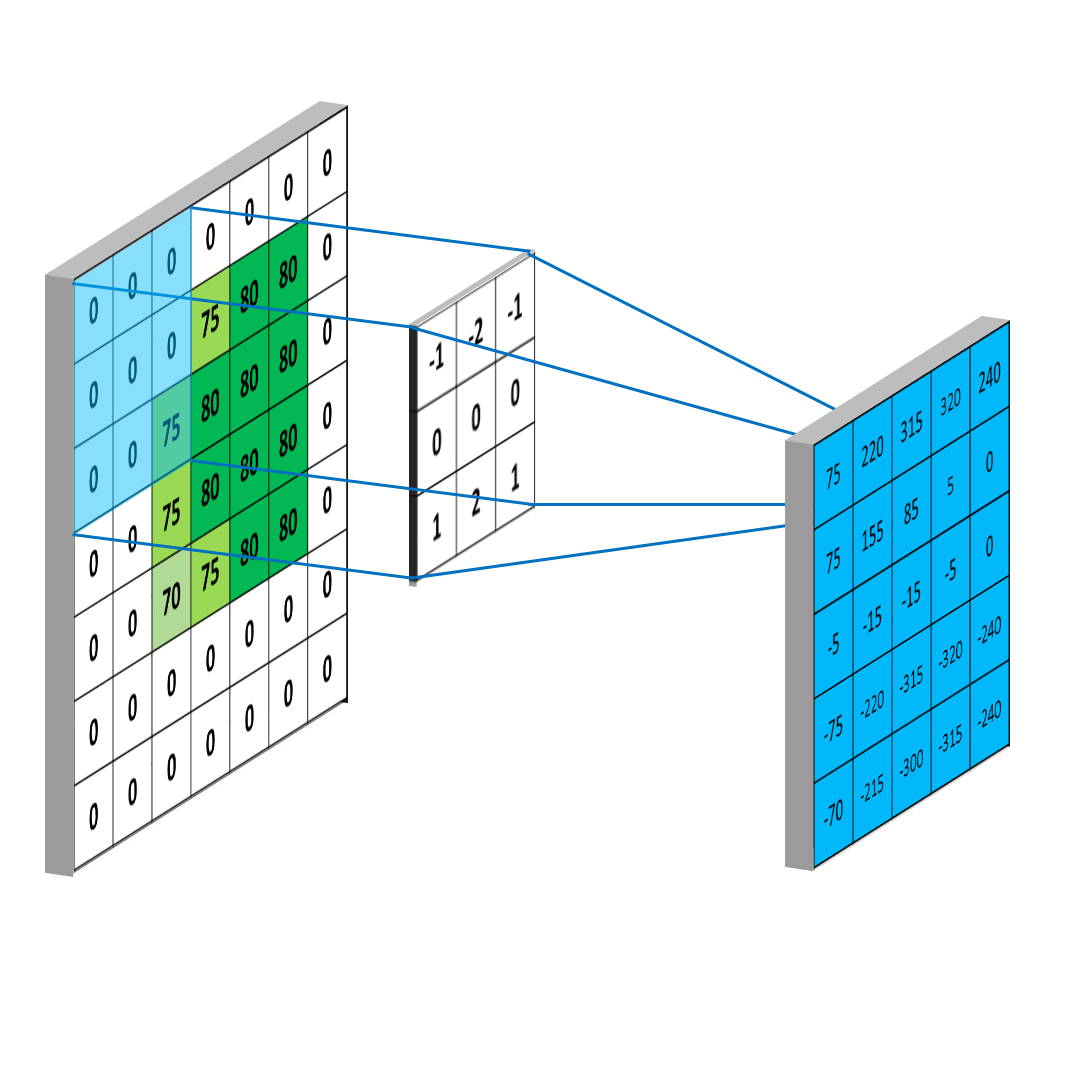
将卷积核放置在图像的左上角。卷积核覆盖的像素值与相应的卷积核值相乘,并将乘积结果求和。结果放置在新图像中,对应于卷积核的中心点。下图显示了这个过程的一个示例。它使用垂直Sobel滤波器(用于边缘检测)并将其应用于图像的像素。
卷积核每次移动一个像素,这个过程会重复进行,直到图像中的所有可能位置都被过滤,就像下面这样,这次是针对水平Sobel滤波器。请注意,在卷积后的图像周围有一个空值边框。这是因为卷积的结果放置在卷积核的中心位置。为了解决这个问题,使用了一种称为“填充”或更常见的“零填充”的过程。这意味着在原始图像周围放置一个由零组成的边框,使其在四周增加一个像素的宽度。然后按照正常方式进行卷积,但卷积结果将产生一个与原始图像大小相等的图像。
零填充被用来确保卷积后的图像不会缩小。通过在原始图像周围添加零值边框,图像的尺寸有效增加,使得卷积操作可以在不减小输出尺寸的情况下进行。这在应用需要输出图像与输入图像具有相同尺寸的滤波器或卷积时尤为重要。
现在我们有了卷积后的图像,我们可以使用一个颜色映射来可视化结果。在这里,我只是将值归一化到0到255之间,以便可以应用灰度可视化:
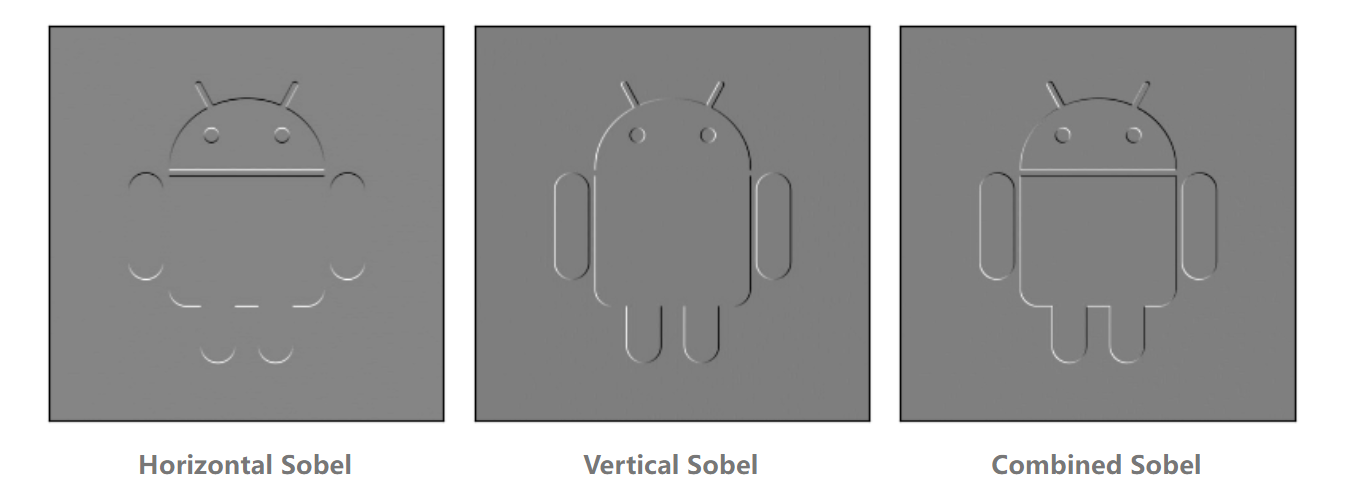
这个虚拟示例可能代表了Android头部的左下角,但并不真正看起来像是检测到了什么。为了看到正确的效果,我们需要将其放大,以便不只是查看单个像素。对完整的264 x 264图像进行水平和垂直Sobel滤波得到的结果如下:
我们还将两个滤波器的结果相加,以获得水平和垂直的结果。
卷积神经网络(Convolutional Neural Networks,CNNs)是一种特别擅长分析和处理图像的深度学习模型。在CNN中,卷积的概念在其中起着关键作用。
在CNN中,卷积用于从输入图像中提取特征。该过程涉及将一组可学习的滤波器,也称为卷积核,应用于输入图像上。每个卷积核都是一个小的权重矩阵,通过在图像上滑动并执行逐元素乘法和求和操作来与图像进行卷积。这个卷积操作产生一个卷积图像,其中每个像素代表一个特征。
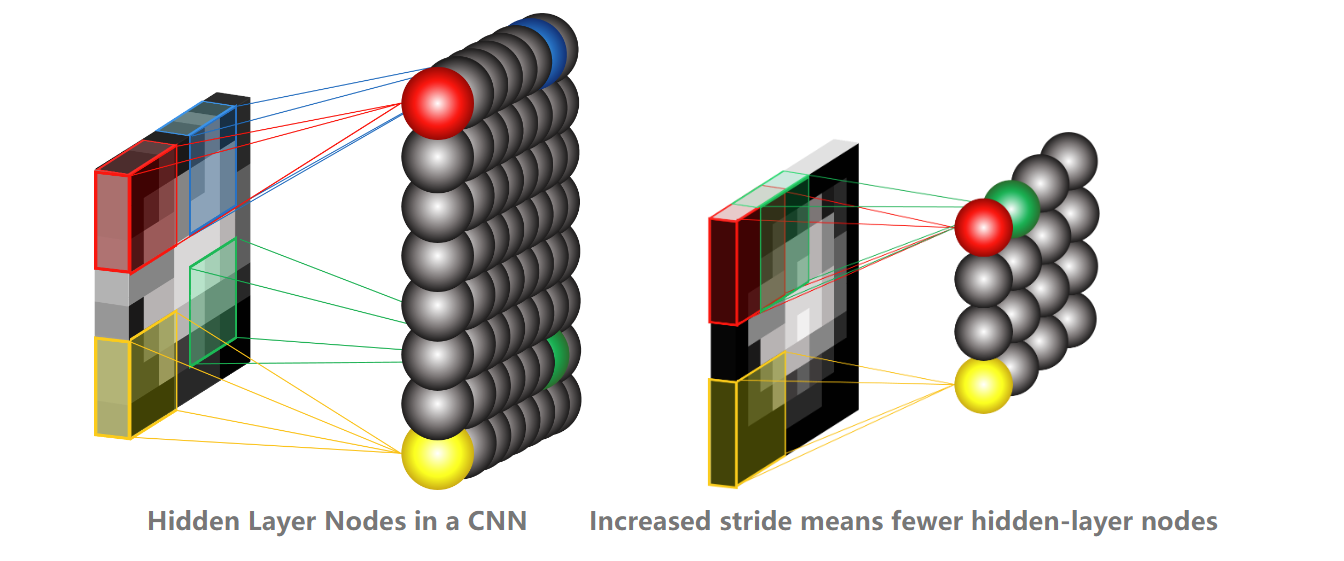
输入图像中的每个像素都被视为一个特征,并对应于CNN中的一个输入节点。每个卷积操作的结果被传递到下一层,其中卷积图像的每个特征或像素成为隐藏层中的一个节点。
卷积核中的权重充当着连接输入图像特征和隐藏层节点之间的连接。隐藏节点的数量与输入节点数量相同,稍作调整以考虑零填充。这意味着隐藏层也是二维的,就像输入图像一样。步幅(stride)决定了卷积核在图像上的移动方式,可以调整步幅来增加或减少隐藏节点或卷积图像中的像素数量。
连接隐藏层节点的权重需要通过类似于常规神经网络的学习过程来学习。图像通过这些节点(通过与权重即卷积核进行卷积)传递,并将结果与期望输出进行比较。然后,通过反向传播和优化来更新权重。
实际上,并不仅仅需要学习单个权重或卷积核。隐藏层中存在一整组节点,每个节点都关注图像的同一区域。该行中的每个节点都尝试学习不同的卷积核(不同的权重),以捕捉图像的不同特征,例如边缘。这样,隐藏层可能看起来更像是这样的:
深度学习的关键在于每个隐藏层都能够学习大量的卷积核。来自一个隐藏层的输出然后传递给后续层,后续层可以根据前一层输出的卷积图像来学习自己的卷积核。这种分层学习过程允许CNN从边缘和早期层次中检测到的小特征中检测和构建更复杂的特征。
3.卷积神经网络的基本结构
CNN的架构赋予了它强大的能力。许多关于CNN的论文倾向于讨论新的架构,即不同层的数量和顺序,以及学习了多少个卷积核。然而,往往是对旧架构应用的巧妙技巧真正增强了网络的能力。现在,让我们来看看CNN中的其他层。
3.1输入层
输入图像被放置在这一层。它可以是单层的2D图像(灰度图),2D的3通道图像(RGB彩色图)或3D图像。输入的排列方式的主要区别在于期望的卷积核形状的形成。需要学习与输入相同深度的卷积核,例如对于一个5 x 5尺寸的2D RGB图像,卷积核的尺寸应为5 x 5 x 3。
当CNN的输入具有某些特定尺寸时,似乎效果最好。这是由于卷积的行为。根据卷积核的步幅和随后的池化层,输出可能会变成“非法”尺寸,包括半像素。我们将在池化层部分进一步讨论这个问题。
3.2卷积层
我们已经了解了卷积层的作用。只需记住,它接收一个图像,例如[56 x 56 x 3],假设步幅为1且进行零填充,如果学习了32个卷积核,则会产生一个[56 x 56 x 32]的输出。重要的是要注意,在Python中实现CNN时,这些维度的顺序可能很重要。这是因为涉及到了大量的矩阵乘法运算!
3.3非线性
这里的“非线性”并不是CNN的一个独立层,而是作为卷积层的一部分,在神经元的输出上进行操作(就像普通的神经网络一样)。这意味着“不要将数据按原样直接传递(线性),而是对其进行一些操作(非线性),以便在后续阶段更好地利用它”。
在我们的神经网络教程中,我们介绍了不同的激活函数。每个激活函数都提供了输入到输出的不同映射,要么是到[-1, 1],要么是到[0, 1],或者是到其他域,例如ReLU(修正线性单元)在0处对数据进行阈值处理:max(0,x)。ReLU非常受欢迎,因为它不需要任何昂贵的计算,并且已经证明可以加速随机梯度下降算法的收敛速度。
3.4池化层
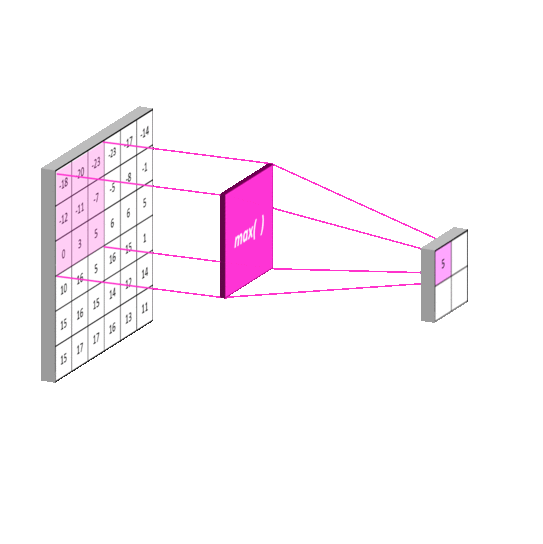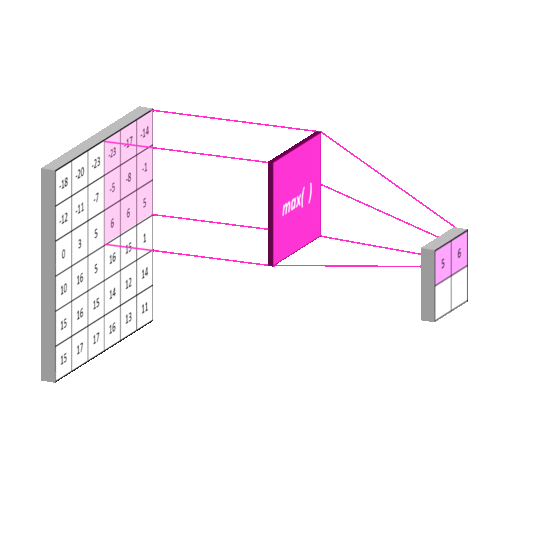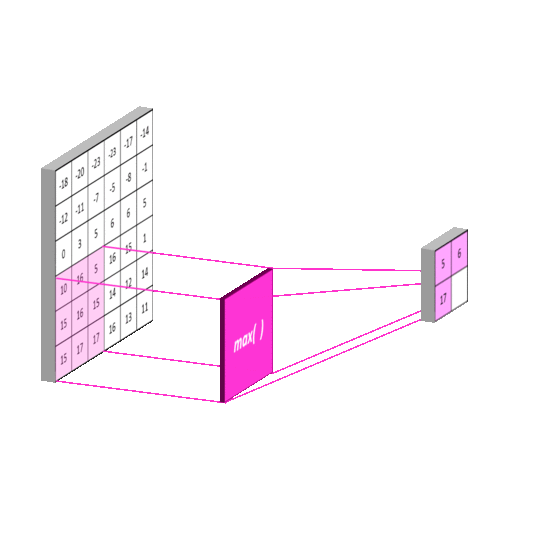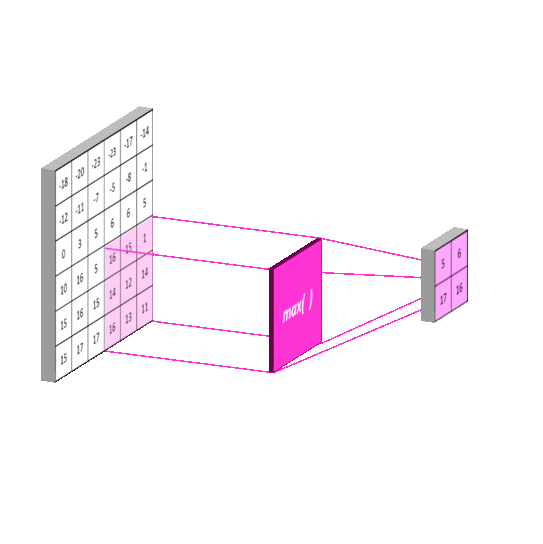
池化层对于确保CNN的后续层能够捕捉到比边缘和曲线更大尺度的细节非常关键。它通过在尝试在图像上学习卷积核之前,合并卷积图像中的像素区域(缩小图像)来实现这一点。实际上,这个阶段采用另一个卷积核,例如[2 x 2],并像卷积一样在整个图像上滑动。通常步幅和卷积核大小相等,例如[2 x 2]的卷积核步幅为2。这个例子将使卷积图像的尺寸减半。由学习的卷积核产生的特征图数量保持不变,因为池化是逐个特征图进行的。因此,池化层返回的数组与卷积层具有相同的深度。下图展示了这个原理。
最大池化是CNN中常用的一种操作,它有助于减小特征图的尺寸并提取重要的特征。通过使用步幅等于滤波器大小的最大滤波器,最大池化可以有效地捕捉到图像中的关键特征。
3.5关于感受野的说明
这是一个非常重要但有时被忽视的概念。我们说单个神经元的感受野可以理解为它可以“看到”的图像区域。因此,每个神经元都有不同的感受野。虽然这是正确的,但只有在观察池化之后发生的情况时,才能真正理解它的全部影响。
让我们以一个尺寸为[12 x 12]和第一个卷积层中[3 x 3]的卷积核尺寸为例。卷积层的输出(假设进行零填充和步幅为1)将是[12 x 12 x 10],如果我们学习了10个卷积核。经过使用[3 x 3]的池化核进行池化后,我们得到一个[4 x 4 x 10]的输出。这个输出被馈送到下一个卷积层。假设第二个卷积层的卷积核是[2 x 2],我们会说这里的感受野也是[2 x 2]吗?有些人可能会这样认为,但实际上并不是。事实上,这一层的神经元不仅仅看到了卷积图像的[2 x 2]区域,它实际上还看到了原始图像的[4 x 4]区域。这是第一层[3 x 3]对于第二层“感受野”中每个像素的贡献(记住我们在第一层使用了步幅为1)。通过对网络的其余部分进行类似的推导,最终可以得到一个具有与原始图像大小相等的感受野的最后一层。理解这一点使我们真正了解了CNN是如何在过程中逐渐构建图像的。
3.6全连接(Dense)层
这一层花了我一些时间来理解,尽管它很简单。如果我考虑最终池化层的所有[3 x 3 x 64]个特征图,我有3 x 3 x 64 = 576个不同的权重要考虑和更新。我需要确保我的训练标签与输出层的输出相匹配。在输出层中,我们可能只有10种可能性(例如在经典的MNIST数字分类任务中的0-9个数字)。因此,我们希望输出层的最终数字为[10,],而在此之前的层为[? x 10],其中?代表全连接(FC)层中的节点数。如果这一层只有一个节点,它将有576个连接到它的权重 - 每个来自前一个池化层的权重都有一个。这对于学习这些低维输出的任何组合来说并不是很有用。将神经元的数量增加到1000个,将使FC层能够提供许多不同的特征组合,并学习表示特征空间的更复杂的非线性函数。这一层中的节点数可以是我们想要的任何值,并不受任何先前维度的限制 - 这就是当我看其他CNN时一直困惑的事情。有时还可以看到两个FC层一起使用,这只是增加了学习复杂函数的可能性。
FC层是一维向量。然而,FC层充当“黑盒子”,且难以解释。它们也容易过拟合,因此通常会进行“dropout”操作(下面讨论)。
将全连接层替换为另一个卷积层,这可能会更好地帮助理解。这个过程非常简单 - 将池化层的输出作为输入,并使用与池化层中特征图相同大小的卷积核对其进行卷积。为了使这个过程有用,卷积层的输入应该经过足够多的池化层,使其尺寸缩小到大约[5 x 5]或[3 x 3]。这样做有什么作用呢?通过将一个[3 x 3]的图像与一个[3 x 3]的卷积核进行卷积,我们得到一个像素的输出。没有步幅,每个特征图只进行一次卷积。因此,这一层的输出将是一个[1 x k]的向量,其中k是特征图的数量。这与全连接层非常相似,只是卷积的输出仅来自单个特征图,而不是与所有特征图相连接。
但是,这不是更多要学习的权重吗?是的,所以我们不这样做。相反,我们执行全局平均池化(global average pooling)或全局最大池化(global max pooling),其中全局指的是单个特征图(而不是整个特征图集合)。因此,我们对特征中的所有点取平均,并将其重复应用于每个特征,以获得与之前相同的[1 x k]向量。请注意,最后一个卷积层中的通道数(卷积核/特征数)必须等于我们想要的输出数,否则我们必须包含一个全连接层将[1 x k]向量转换为所需的输出。
这种方法非常强大,因为我们通过一个像素表示了一个非常大的感受野,并且还去除了一些空间信息,使我们能够尝试考虑输入的平移。我们能够说,如果输出的值很高,那么所有对该输出可见的特征图都已经激活足够,以表示一个“猫”或我们训练网络学习的其他内容。
3.7 Dropout层
前面提到的全连接层与前一层的所有权重相连接 - 这可能是一个非常大的数量。因此,全连接层容易过拟合,意味着网络在新数据上的泛化能力不好。有许多技术可以用来减少过拟合,但在CNN中最常见的是Hinton提出的dropout层。顾名思义,这会使网络在每次迭代中以一定的概率“丢弃”一些节点。保留概率介于0和1之间,通常在0.2-0.5左右。这是一个特定节点在训练过程中被丢弃的概率。当进行反向传播时,与这些节点相连的权重不会被更新。它们将在下一次迭代之前重新添加,然后再选择另一组进行dropout。
3.8 输出层
当然,根据CNN的目的,输出层会有所不同。一般来说,输出层由多个节点组成,如果它们是“真实的”或被激活的,则具有较高的值。考虑一个分类问题,CNN给出了一组包含猫、狗和大象的图像。如果我们要求CNN学习猫、狗和大象的外观,输出层将是一组三个节点,每个节点代表一个“类别”或动物。我们期望当CNN找到一张猫的图像时,代表“猫”的节点的值比其他两个节点更高。这与常规神经网络的思想相同。实际上,全连接层和输出层可以被视为传统的神经网络,通常还包括softmax激活函数。某些输出层是概率,因此它们的总和为1,而其他输出层只能达到一个值,该值可以是0-255范围内的像素强度。如果我们进行回归或决定图像是否属于特定类别(例如患病或健康),输出也可以由单个节点组成。然而,通常情况下,即使是二元分类也会在输出中使用2个节点,并使用“one-hot”编码的标签进行训练,例如类别0为[1,0],类别1为[0,1]。
反向传播的说明
我发现将CNN反向考虑对理解很有帮助。一开始,我无法理解CNN首先学习各种不同类型的边缘、曲线等,然后将它们组合成大的特征,例如人脸。在与同事的讨论中,我们认为可以将CNN反向工作,实际上这就是发生的情况 - 反向传播将权重从最后一层向第一层更新。实际上,误差(或损失)最小化首先发生在最后一层,因此这是网络“看到”整体情况的地方。梯度(权重的更新)在输入层逐渐消失,在输出层最大。我们可以有效地认为CNN在输出层学习“人脸 - 有眼睛、鼻子、嘴巴”,然后在前一层学习“我不知道什么是人脸,但这里有一些眼睛、鼻子、嘴巴”,然后是“眼睛是什么?我只看到圆圈、一些白色部分和一个黑洞”,接着是“哇!圆形的东西!”最初是“我认为那就是一条线”。也许我们可以认为CNN在第一层对自己的判断不太确定,在最后一层更加先进。
CNN可以用于分割、分类、回归和其他各种处理。总的来说,它们只有四个不同之处:
架构(卷积、池化和全连接层的数量和顺序,以及卷积核的大小和数量) 输出(概率等) 训练方法(成本或损失函数、正则化和优化器) 超参数(学习率、正则化权重、批量大小、迭代次数等) 可能还有其他更详细地考虑这些问题的帖子,但现在我希望您对CNN的工作原理有一些了解。现在,让我们开始编码吧…
4.数据增强技术
训练有效的深度学习框架的最大限制因素之一是训练数据的可用性、质量和组织方式。为了在分类任务中表现良好,我们需要尽可能多地展示给我们的卷积神经网络等模型许多示例。然而,在某些情况下,这并不总是可能的,特别是在难以收集训练数据的情况下,例如医学图像数据。在本文中,我们将学习如何应用数据增强策略来充分利用我们有限数量的示例的n维图像。
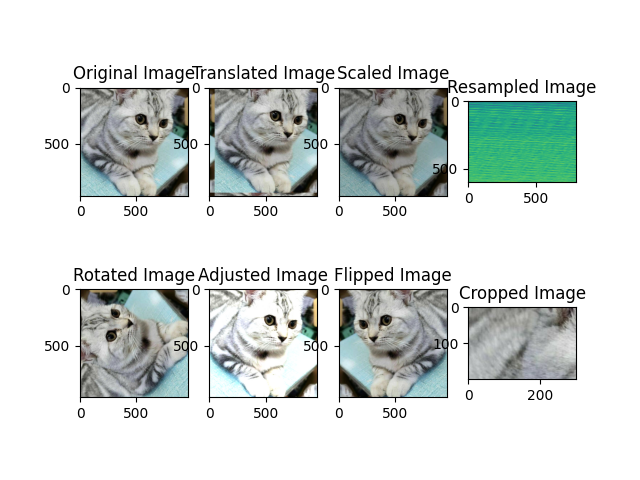
通过对图像进行平移、旋转、缩放、强度增强和翻转等操作,我们可以生成更多样化的数据。尽管在视觉上这些变换可能不会明显改变图像,但从数值上来看,它们可能会产生完全不同的图像。例如,将一组图像逐个像素向右平移,每个图像与前一个图像相比都有微小的变化。在某个特定位置上,每个像素的颜色、周围平均强度等都会有所不同。卷积神经网络在进行卷积操作和权重决策时会考虑到这些值。通过向卷积神经网络提供经过平移和旋转等变换的图像集合,我们可以使其学习对这些变换具有不变性。(例如下面的猫图像)
4.1 Translation(平移)
平移是一种数据增强技术,通过将图像沿着水平和垂直方向移动一定的像素距离来创建新的图像。平移可以改变图像中物体的位置,从而增加数据集的多样性。这有助于模型学习到对象在不同位置的特征。
代码示例:
def translate_image(image, shift_x, shift_y):
translated_image = np.roll(image, (shift_y, shift_x), axis=(0, 1))
return translated_image
4.2 Scaling(缩放)
缩放是一种数据增强技术,通过调整图像的尺寸来改变其大小。缩放可以使图像变大或变小,从而增加数据集的多样性。缩放可以改变物体的比例和大小。
代码示例:
def scale_image(image, scale_factor):
scaled_image = np.clip(image * scale_factor, 0, 255).astype(np.uint8)
return scaled_image
4.3 Resampling(重采样)
重采样是一种数据增强技术,通过改变图像的分辨率来创建新的图像。重采样可以增加或减少图像的像素数量,从而改变图像的清晰度和细节。重采样可以用于模型训练时需要不同分辨率的图像。
代码示例:
def resample_image(image, new_width, new_height):
resampled_image = np.clip(np.round(image), 0, 255).astype(np.uint8)
resampled_image = np.resize(resampled_image, (new_height, new_width))
return resampled_image
4.4 Rotation(旋转)
旋转是一种数据增强技术,通过将图像按照指定的角度进行旋转来创建新的图像。旋转可以改变图像中物体的方向和角度,增加数据集的多样性。旋转可以使模型学习到不同角度下的物体特征。
代码示例:
def rotate_image(image, angle):
rotated_image = np.rot90(image, k=int(angle/90))
return rotated_image
4.5 Intensity Changes(强度变换)
强度变换是一种数据增强技术,通过改变图像的亮度、对比度或颜色来创建新的图像。强度变换可以使图像的外观发生变化,增加数据集的多样性。强度变换可以用于模型学习到不同光照条件下的物体特征。
代码示例:
def change_intensity(image, brightness_factor, contrast_factor):
adjusted_image = np.clip(image * contrast_factor + brightness_factor, 0, 255).astype(np.uint8)
return adjusted_image
4.6 Flipping(翻转)
翻转是一种数据增强技术,通过将图像沿着水平或垂直方向进行翻转来创建新的图像。翻转可以改变图像中物体的方向,增加数据集的多样性。翻转可以使模型学习到物体在不同方向上的特征。
代码示例:
def flip_image(image, flip_code):
flipped_image = np.flip(image, axis=flip_code)
return flipped_image
4.7 Cropping(裁剪)
裁剪是一种数据增强技术,通过从图像中选择感兴趣的区域来创建新的图像。裁剪可以改变图像中物体的位置和大小,增加数据集的多样性。裁剪可以使模型学习到不同尺寸和位置的物体特征。
代码示例:
def crop_image(image, x, y, width, height):
cropped_image = image[y:y+height, x:x+width]
return cropped_image
5.池化
池化(Pooling)是卷积神经网络(CNN)中的一种操作,它可以减少特征图的大小,同时保留重要的信息。池化通常在卷积层之后使用,它可以帮助网络学习更抽象的特征,并减少过拟合的风险。
5.1池化的分类
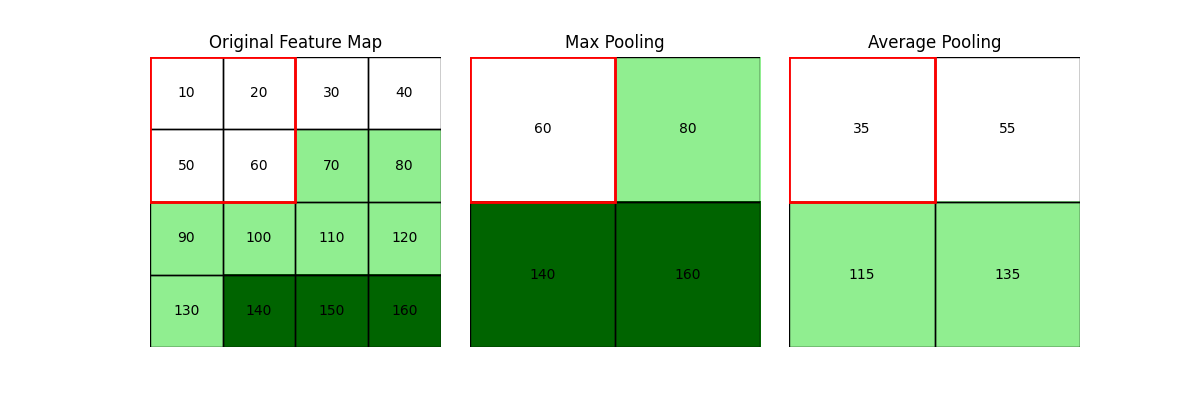
池化有两种主要类型:最大池化(Max Pooling)和平均池化(Average Pooling)。
最大池化
最大池化操作将特征图中的每个区域的最大值作为输出。例如,如果池化窗口大小为 2x2,则最大池化操作将把特征图中的每个 2x2 区域的最大值作为输出。
最大池化操作可以帮助网络学习更鲁棒的特征,因为它可以减少噪声和无关信息的影响。然而,最大池化操作也会丢失一些信息,因为它只保留了每个区域的最大值。
平均池化
平均池化操作将特征图中的每个区域的平均值作为输出。例如,如果池化窗口大小为 2x2,则平均池化操作将把特征图中的每个 2x2 区域的平均值作为输出。
平均池化操作可以帮助网络学习更平滑的特征,因为它可以减少噪声和无关信息的影响。然而,平均池化操作也会丢失一些信息,因为它只保留了每个区域的平均值。
5.2池化的好处
池化操作可以带来以下好处:
- 减少特征图的大小,从而减少计算量和内存消耗。
- 帮助网络学习更抽象的特征。
- 减少过拟合的风险。
5.3 池化的缺点
池化操作也有一些缺点:
- 会丢失一些信息。
- 可能导致特征图变得过于平滑。
5.4 池化的应用
池化操作广泛应用于各种计算机视觉任务,例如图像分类、目标检测和语义分割。
第4篇经典热门网络结构
1.LeNet-5
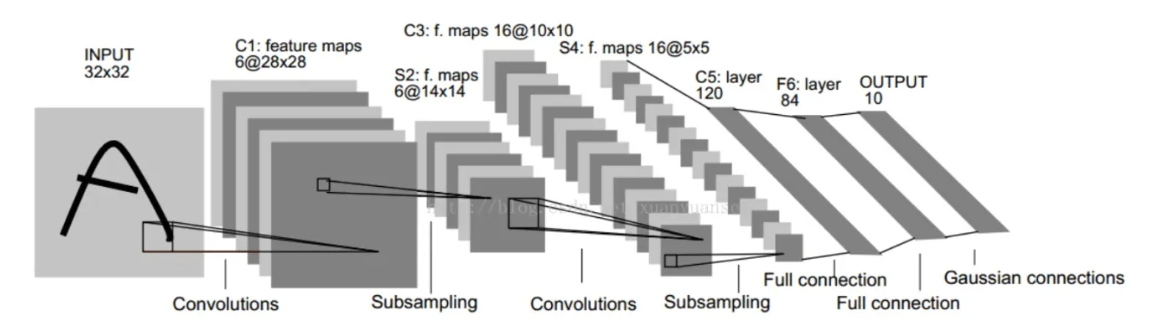
LeNet-5是由Yann LeCun等人于1998年提出的经典卷积神经网络结构,用于手写数字识别任务。它由卷积层、池化层和全连接层组成。
模型结构: LeNet-5的模型结构如下:
- 输入层:接受灰度图像作为输入,图像尺寸为32×32像素。
- 卷积层C1:使用6个5×5的卷积核对输入图像进行卷积操作,得到6个特征图。每个特征图的尺寸为28×28像素。
- 池化层S2:使用2×2的最大池化操作,对C1层的特征图进行下采样,将特征图的尺寸减半,得到6个14×14的特征图。
- 卷积层C3:使用16个5×5的卷积核对S2层的特征图进行卷积操作,得到16个10×10的特征图。
- 池化层S4:使用2×2的最大池化操作,对C3层的特征图进行下采样,将特征图的尺寸减半,得到16个5×5的特征图。
- 全连接层C5:将S4层的特征图展平为一个向量,并与权重矩阵相乘,得到120维的特征向量。
- 全连接层F6:将C5层的特征向量与权重矩阵相乘,得到84维的特征向量。
- 输出层:是一个全连接层,将F6层的特征向量与权重矩阵相乘,得到10维的输出向量,表示0-9的数字类别。
模型特性: LeNet-5具有以下特性:
- 层次结构:LeNet-5采用了多层的卷积和池化操作,通过逐层提取特征,实现了对图像的层次化表示。
- 参数共享:LeNet-5中的卷积层使用了参数共享的机制,即每个卷积核在整个输入图像上进行卷积操作,从而减少了参数量。
- 非线性激活函数:LeNet-5使用了Sigmoid作为激活函数,引入了非线性变换,增强了网络的表达能力。
- 池化操作:LeNet-5中的池化层通过下采样操作减小了特征图的尺寸,提取了更加鲁棒的特征,并减少了计算量。
- 手写数字识别:LeNet-5最初设计用于手写数字识别任务,对于这个任务具有较好的性能和泛化能力。
LeNet-5的成功证明了卷积神经网络在图像处理任务中的有效性,为后续的深度学习研究和应用奠定了基础。虽然LeNet-5相对于现代的深度卷积神经网络来说较为简单,但它的思想和结构对于理解卷积神经网络的基本原理和发展历程仍然具有重要意义。
2.AlexNet
AlexNet是由Alex Krizhevsky等人于2012年在ImageNet图像分类竞赛中提出的卷积神经网络结构。它是一个较深的网络,包含多个卷积层和全连接层,并使用了ReLU激活函数和Dropout正则化技术。
AlexNet是由Alex Krizhevsky等人于2012年提出的卷积神经网络模型,它在ImageNet图像分类竞赛中取得了显著的突破,标志着深度学习在计算机视觉领域的崛起。
模型结构: AlexNet的模型结构如下:
- 输入层:接受RGB图像作为输入,图像尺寸为227×227像素。
- 卷积层C1:使用96个11×11的卷积核对输入图像进行卷积操作,得到96个特征图。每个特征图的尺寸为55×55像素。
- 激活层ReLU1:对C1层的特征图进行ReLU激活函数操作,增加网络的非线性表达能力。
- 池化层S2:使用3×3的最大池化操作,对C1层的特征图进行下采样,将特征图的尺寸减半,得到96个27×27的特征图。
- 卷积层C3:使用256个5×5的卷积核对S2层的特征图进行卷积操作,得到256个27×27的特征图。
- 激活层ReLU2:对C3层的特征图进行ReLU激活函数操作。
- 池化层S4:使用3×3的最大池化操作,对C3层的特征图进行下采样,将特征图的尺寸减半,得到256个13×13的特征图。
- 卷积层C5:使用384个3×3的卷积核对S4层的特征图进行卷积操作,得到384个13×13的特征图。
- 激活层ReLU3:对C5层的特征图进行ReLU激活函数操作。
- 卷积层C6:使用384个3×3的卷积核对C5层的特征图进行卷积操作,得到384个13×13的特征图。
- 激活层ReLU4:对C6层的特征图进行ReLU激活函数操作。
- 卷积层C7:使用256个3×3的卷积核对C6层的特征图进行卷积操作,得到256个13×13的特征图。
- 激活层ReLU5:对C7层的特征图进行ReLU激活函数操作。
- 池化层S5:使用3×3的最大池化操作,对C7层的特征图进行下采样,将特征图的尺寸减半,得到256个6×6的特征图。
- 全连接层F6:将S5层的特征图展平为一个向量,并与权重矩阵相乘,得到4096维的特征向量。
- 激活层ReLU6:对F6层的特征向量进行ReLU激活函数操作。
- Dropout层:随机丢弃一部分神经元,防止过拟合。
- 全连接层F7:将Dropout层的输出与权重矩阵相乘,得到4096维的特征向量。
- 激活层ReLU7:对F7层的特征向量进行ReLU激活函数操作。
- Dropout层:再次随机丢弃一部分神经元。
- 输出层:是一个全连接层,将Dropout层的输出与权重矩阵相乘,得到1000维的输出向量,表示ImageNet数据集的1000个类别。
模型特性: AlexNet具有以下特性:
- 深度网络:相对于之前的模型,AlexNet是一个较深的网络,通过增加网络的深度,可以提取更加抽象和高级的特征。
- 大型卷积核:AlexNet使用了较大的卷积核(11×11和5×5),这样可以增加感受野,提取更大范围的特征。
- 局部响应归一化(LRN):在AlexNet的激活层之间使用了LRN操作,它可以增强特征的鲁棒性,提高模型的泛化能力。
- Dropout正则化:AlexNet引入了Dropout层,通过随机丢弃一部分神经元,可以减少过拟合,提高模型的泛化能力。
- 并行计算:AlexNet使用了两个GPU进行并行计算,这在当时是一项创新,大大加快了训练速度。
AlexNet的突破性成果证明了深度卷积神经网络在图像分类任务中的优越性能,为后续的深度学习研究和应用奠定了基础。它的成功也促进了对更深、更复杂的网络结构的探索和发展。
3.VGGNet
VGGNet是由Karen Simonyan和Andrew Zisserman于2014年提出的卷积神经网络模型,它在ImageNet图像分类竞赛中取得了优秀的成绩。VGGNet的主要特点是采用了多个小尺寸的卷积核来代替大尺寸的卷积核,从而增加了网络的深度。
模型结构: VGGNet的模型结构如下:
- 输入层:接受RGB图像作为输入,图像尺寸为224×224像素。
- 卷积层:VGGNet使用多个连续的3×3的卷积核进行卷积操作,卷积核的数量和层数可以根据具体的网络配置进行调整。每个卷积层后面都跟着一个ReLU激活函数。
- 池化层:在每个卷积层之后,VGGNet使用2×2的最大池化操作进行下采样,将特征图的尺寸减半。
- 全连接层:在卷积层之后,VGGNet使用几个全连接层来进行分类。每个全连接层后面都跟着一个ReLU激活函数。
- 输出层:最后一个全连接层的输出通过Softmax函数进行分类,得到图像的类别概率。
VGGNet的一个重要特点是网络的深度,它可以有16层或19层,具体取决于网络的配置。其中VGG16有13个卷积层和3个全连接层,VGG19有16个卷积层和3个全连接层。
模型特性: VGGNet具有以下特性:
- 网络深度:VGGNet相对于之前的模型来说更深,通过增加网络的深度,可以提取更加抽象和高级的特征。
- 小尺寸卷积核:VGGNet使用多个3×3的卷积核来代替较大尺寸的卷积核,这样可以增加网络的深度,同时减少了参数量。
- 均匀的网络结构:VGGNet的网络结构非常均匀,每个卷积层后面都跟着一个池化层,然后是一个全连接层,这种均匀的结构使得网络更容易理解和实现。
- 较小的卷积核和池化层:VGGNet使用较小的卷积核和池化层,这样可以增加感受野,提取更大范围的特征。
- 较小的步长:VGGNet使用步长为1的卷积操作,这样可以保留更多的空间信息。
VGGNet的成功证明了增加网络深度和使用小尺寸卷积核的重要性,为后续的深度卷积神经网络研究和应用提供了重要的启示。虽然VGGNet相对于现代的深度卷积神经网络来说较为简单,但它的思想和结构对于理解卷积神经网络的基本原理和发展历程仍然具有重要意义。
4.GoogLeNet
GoogLeNet是由Google团队于2014年提出的卷积神经网络模型,它在ImageNet图像分类竞赛中取得了优秀的成绩。GoogLeNet的主要特点是采用了Inception模块,通过并行使用不同尺寸的卷积核和池化操作来提取多尺度的特征。
模型结构: GoogLeNet的模型结构如下:
- 输入层:接受RGB图像作为输入,图像尺寸为224×224像素。
- Inception模块:GoogLeNet使用多个Inception模块来构建网络。每个Inception模块由多个并行的卷积层和池化层组成,这些层具有不同尺寸的卷积核和池化操作。通过并行使用不同尺寸的卷积核和池化操作,Inception模块可以提取多尺度的特征。
- 全局平均池化层:在最后一个Inception模块之后,GoogLeNet使用一个全局平均池化层,将特征图的尺寸变为1×1,得到固定长度的特征向量。
- Dropout层:在全局平均池化层之后,GoogLeNet使用Dropout层来减少过拟合。
- 全连接层:最后一个全连接层将Dropout层的输出与权重矩阵相乘,得到1000维的输出向量,表示ImageNet数据集的1000个类别。
模型特性: GoogLeNet具有以下特性:
- Inception模块:GoogLeNet引入了Inception模块,通过并行使用不同尺寸的卷积核和池化操作,可以提取多尺度的特征,增加网络的表达能力。
- 参数共享:在Inception模块中,不同尺寸的卷积核和池化操作共享相同的输入,这样可以减少参数量,提高模型的效率。
- 1×1卷积:GoogLeNet使用了1×1的卷积核来进行降维操作,减少特征图的通道数,从而降低计算量。
- 辅助分类器:GoogLeNet在中间层添加了辅助分类器,用于在训练过程中提供额外的梯度信号,帮助网络更快地收敛。
- 平均池化:GoogLeNet使用全局平均池化层来代替全连接层,减少参数量,避免过拟合。
GoogLeNet的成功证明了Inception模块的有效性和参数共享的重要性,为后续的深度卷积神经网络研究和应用提供了重要的启示。它的创新性设计和高效的特征提取能力使得GoogLeNet成为了深度学习中的经典模型之一。
5.ResNet
ResNet(残差网络)是由Kaiming He等人于2015年提出的卷积神经网络模型,它在ImageNet图像分类竞赛中取得了显著的突破。ResNet的主要特点是引入了残差连接,通过跳跃连接将输入直接传递到输出,解决了深层网络中的梯度消失和梯度爆炸问题。
模型结构: ResNet的模型结构如下:
- 输入层:接受RGB图像作为输入,图像尺寸为224×224像素。
- 卷积层和池化层:ResNet开始于一个普通的卷积层和池化层,用于提取初始特征。
- 残差块:ResNet的核心是由多个残差块组成的。每个残差块由两个或三个卷积层组成,其中包含了跳跃连接。跳跃连接将输入直接添加到输出中,使得网络可以学习残差函数。
- 全局平均池化层:在最后一个残差块之后,ResNet使用全局平均池化层将特征图的尺寸变为1×1,得到固定长度的特征向量。
- 全连接层:最后一个全连接层将全局平均池化层的输出与权重矩阵相乘,得到1000维的输出向量,表示ImageNet数据集的1000个类别。
模型特性: ResNet具有以下特性:
- 残差连接:ResNet引入了残差连接,通过跳跃连接将输入直接传递到输出,解决了深层网络中的梯度消失和梯度爆炸问题。残差连接允许网络更容易地学习恒等映射,从而提高了网络的性能。
- 深度网络:相对于之前的模型,ResNet是一个非常深的网络,通过增加网络的深度,可以提取更加抽象和高级的特征。
- 参数共享:在残差块中,不同层之间共享相同的权重,这样可以减少参数量,提高模型的效率。
- 预训练和微调:由于ResNet的深度和复杂性,通常使用预训练的模型来初始化网络权重,并通过微调进行进一步的训练。
- 高性能和泛化能力:ResNet在ImageNet图像分类竞赛中取得了优秀的成绩,证明了其在大规模图像分类任务中的高性能和泛化能力。
ResNet的创新性设计和引入的残差连接使得它成为了深度学习中的重要里程碑,对于解决深层网络中的梯度问题和构建更深的网络具有重要意义。它的成功也促进了对更深、更复杂的网络结构的探索和发展。
6.DenseNet
DenseNet是由Gao Huang等人于2016年提出的卷积神经网络模型,它在ImageNet图像分类竞赛中取得了优秀的成绩。DenseNet的主要特点是引入了密集连接,将每一层的输出与之前所有层的输出连接在一起,从而增加了信息流动和特征重用。
模型结构: DenseNet的模型结构如下:
- 输入层:接受RGB图像作为输入,图像尺寸为224×224像素。
- 卷积层和池化层:DenseNet开始于一个普通的卷积层和池化层,用于提取初始特征。
- Dense块:DenseNet的核心是由多个Dense块组成的。每个Dense块由多个密集连接的卷积层组成,其中包含了跳跃连接。每个卷积层的输入是前面所有卷积层的输出的连接。
- 过渡层:在Dense块之间,DenseNet使用过渡层来减小特征图的尺寸和通道数。过渡层包括一个1×1的卷积层和一个2×2的平均池化层。
- 全局平均池化层:在最后一个Dense块之后,DenseNet使用全局平均池化层将特征图的尺寸变为1×1,得到固定长度的特征向量。
- 全连接层:最后一个全连接层将全局平均池化层的输出与权重矩阵相乘,得到1000维的输出向量,表示ImageNet数据集的1000个类别。
模型特性: DenseNet具有以下特性:
- 密集连接:DenseNet引入了密集连接,将每一层的输出与之前所有层的输出连接在一起,使得信息可以在网络中自由流动,增加了特征的重用和信息传递。
- 参数共享:在Dense块中,不同层之间共享相同的权重,这样可以减少参数量,提高模型的效率。
- 特征重用:由于密集连接的存在,每一层都可以直接访问之前所有层的特征图,从而增加了特征的重用,提高了模型的表达能力。
- 减少梯度消失:由于密集连接的存在,梯度可以更容易地在网络中传播,减少了梯度消失的问题,使得网络更易于训练。
- 高性能和泛化能力:DenseNet在ImageNet图像分类竞赛中取得了优秀的成绩,证明了其在大规模图像分类任务中的高性能和泛化能力。
DenseNet的创新性设计和引入的密集连接使得它成为了深度学习中的重要模型之一。它在特征重用、梯度传播和模型性能方面的优势为后续的深度卷积神经网络研究和应用提供了重要的启示。
7.MobileNet
MobileNet是由Google团队于2017年提出的轻量级卷积神经网络模型,旨在在计算资源受限的设备上实现高效的图像分类和目标检测。MobileNet的主要特点是采用了深度可分离卷积和逐点卷积来减少参数量和计算量。
模型结构: MobileNet的模型结构如下:
- 输入层:接受RGB图像作为输入,图像尺寸为224×224像素。
- 卷积层:MobileNet使用多个深度可分离卷积层进行特征提取。深度可分离卷积由深度卷积和逐点卷积两个步骤组成。深度卷积在每个输入通道上进行卷积操作,逐点卷积在每个位置上对所有通道进行卷积操作。
- 空间平均池化层:在最后一个深度可分离卷积层之后,MobileNet使用空间平均池化层将特征图的尺寸变为1×1,得到固定长度的特征向量。
- 全连接层:最后一个全连接层将空间平均池化层的输出与权重矩阵相乘,得到1000维的输出向量,表示ImageNet数据集的1000个类别。
模型特性: MobileNet具有以下特性:
- 深度可分离卷积:MobileNet引入了深度可分离卷积,将标准卷积操作分解为深度卷积和逐点卷积两个步骤。深度可分离卷积可以减少参数量和计算量,从而实现轻量级的模型。
- 逐点卷积:MobileNet使用逐点卷积来进行特征融合,逐点卷积在每个位置上对所有通道进行卷积操作,从而增加特征的非线性表达能力。
- 参数共享:在深度可分离卷积中,不同位置和通道之间共享相同的权重,这样可以减少参数量,提高模型的效率。
- 轻量级和高效性:MobileNet通过深度可分离卷积和逐点卷积的设计,大大减少了参数量和计算量,使得模型在计算资源受限的设备上具有较高的效率。
- 适用性广泛:由于其轻量级和高效性,MobileNet在移动设备、嵌入式设备和边缘计算等资源受限的场景中得到了广泛应用。
MobileNet的创新性设计和轻量级特性使得它成为了在计算资源受限的设备上进行图像分类和目标检测的理想选择。它的成功证明了深度可分离卷积的有效性,并为后续的轻量级模型设计和优化提供了重要的启示。
第5篇目标检测基础
1.基本概念
1.1 目标检测的定义
目标检测是计算机视觉领域的一个重要任务,旨在识别和定位图像或视频中的特定目标物体。目标检测的目标是在给定图像或视频中,准确地确定目标物体的位置,并将其与其他物体进行区分。
目标检测通常需要完成以下两个主要任务:
- 目标分类:确定图像中存在的目标物体的类别。这意味着将目标物体与预定义的类别进行匹配,例如人、汽车、猫等。
- 目标定位:确定目标物体在图像中的位置。这通常通过绘制边界框(bounding box)来表示目标物体的位置和大小。
目标检测的挑战在于处理不同尺寸、姿态、遮挡、光照变化等因素对目标物体造成的影响。为了解决这些挑战,目标检测方法通常结合了图像特征提取、机器学习和深度学习等技术,以实现高精度和高效率的目标检测。目标检测在许多应用领域中具有广泛的应用,包括智能监控、自动驾驶、人脸识别、物体识别等。
1.2 图像识别四大任务
图像识别是计算机视觉领域的一个重要研究方向,涉及多个任务。其中,常见的四大图像识别任务包括:
- 图像分类(Image Classification):图像分类是最常见的图像识别任务之一,旨在将输入的图像分为不同的预定义类别。例如,给定一张图像,识别出图像中的物体或场景属于哪个类别,如猫、狗、汽车、飞机等。
- 目标检测(Object Detection):目标检测是在图像中同时识别和定位多个目标物体的任务。与图像分类不同,目标检测需要在图像中标记出目标物体的位置,通常使用边界框(bounding box)来表示目标的位置和大小。目标检测常用于物体识别、行人检测、交通标志检测等应用。
- 语义分割(Semantic Segmentation):语义分割是将图像中的每个像素分配到不同的语义类别的任务。与目标检测不同,语义分割不仅要识别目标物体的位置,还要对每个像素进行分类,实现像素级别的分割。语义分割常用于图像分割、医学图像分析、自动驾驶等领域。
- 实例分割(Instance Segmentation):实例分割是在图像中同时识别、定位和分割多个目标物体的任务。与语义分割不同,实例分割需要将每个目标物体分割为不同的实例,即对不同的目标物体进行个体级别的分割。实例分割常用于物体分割、人体姿态估计、遥感图像分析等应用。
这四大图像识别任务在计算机视觉领域中具有广泛的应用,每个任务都有其独特的挑战和解决方法。随着深度学习的发展,基于卷积神经网络的方法在这些任务中取得了显著的进展和突破。
1.2 目标检测的核心问题
目标检测作为计算机视觉领域的重要任务,涉及到一些核心问题,其中包括:
- 目标定位:目标定位是目标检测的核心问题之一。它涉及确定图像中目标物体的位置,通常使用边界框(bounding box)来表示目标的位置和大小。目标定位的准确性对于目标检测的性能至关重要。
- 目标分类:目标分类是目标检测的另一个核心问题。它涉及将检测到的目标物体与预定义的类别进行匹配,即确定目标物体属于哪个类别。目标分类的准确性对于目标检测的结果和应用具有重要影响。
- 目标尺度变化:目标检测需要处理不同尺度的目标物体。目标物体可能在图像中以不同的尺度出现,这对于目标检测算法来说是一个挑战。解决目标尺度变化的问题是目标检测中的重要任务之一。
- 目标遮挡:目标检测需要处理目标物体被其他物体或背景遮挡的情况。目标遮挡会导致目标的部分或全部被遮挡,从而增加了目标检测的难度。解决目标遮挡的问题是目标检测中的重要挑战之一。
- 目标多样性:目标检测需要处理不同类别、形状、大小和姿态的目标物体。目标物体的多样性使得目标检测算法需要具备较强的泛化能力,能够准确地检测和分类各种类型的目标。
- 实时性要求:在一些应用场景中,目标检测需要在实时性要求下进行。例如,自动驾驶、实时监控等领域需要快速准确地检测和定位目标物体。因此,实时性是目标检测中的一个重要问题。
解决这些核心问题是目标检测算法研究的关键,涉及到图像处理、特征提取、机器学习和深度学习等多个领域的技术和方法。随着深度学习的发展,基于卷积神经网络的目标检测方法在这些问题上取得了显著的进展。
2.目标检测算法分类
目标检测算法可以分为两大类:
- 单阶段目标检测算法:单阶段目标检测算法直接从输入图像中预测目标的边界框和类别。这种算法通常速度较快,但精度较低。
- 两阶段目标检测算法:两阶段目标检测算法首先生成候选目标区域,然后对这些候选区域进行分类和回归。这种算法通常速度较慢,但精度较高。
下面分别介绍单阶段目标检测算法和两阶段目标检测算法的代表性算法:
单阶段目标检测算法:
- YOLO系列算法:YOLO系列算法是单阶段目标检测算法的代表性算法。YOLO算法将输入图像划分为多个网格,然后对每个网格预测目标的边界框和类别。YOLO算法的速度非常快,但精度较低。
- SSD系列算法:SSD系列算法也是单阶段目标检测算法的代表性算法。SSD算法将输入图像划分为多个网格,然后对每个网格预测多个目标的边界框和类别。SSD算法的速度也很快,但精度比YOLO算法更高。
两阶段目标检测算法:
- R-CNN系列算法:R-CNN系列算法是两阶段目标检测算法的代表性算法。R-CNN算法首先使用选择性搜索算法生成候选目标区域,然后对这些候选区域进行分类和回归。R-CNN算法的精度很高,但速度较慢。
- Fast R-CNN算法:Fast R-CNN算法是对R-CNN算法的改进。Fast R-CNN算法使用卷积神经网络对候选目标区域进行分类和回归,从而提高了算法的速度。
- Faster R-CNN算法:Faster R-CNN算法是对Fast R-CNN算法的进一步改进。Faster R-CNN算法使用区域建议网络(RPN)生成候选目标区域,从而进一步提高了算法的速度。
3.目标检测基本流程
目标检测的基本流程可以概括为以下几个步骤:
- 输入图像:首先,将待检测的图像输入到目标检测算法中。
- 候选区域生成:在这一步骤中,算法会生成一系列候选目标区域。这些候选区域是可能包含目标的图像区域。
- 特征提取:对于每个候选区域,目标检测算法会提取特征。这些特征可以是传统的计算机视觉特征,如HOG(方向梯度直方图)或SIFT(尺度不变特征变换),也可以是深度学习模型提取的特征,如卷积神经网络(CNN)。
- 目标分类和边界框回归:在这一步骤中,使用提取的特征对每个候选区域进行目标分类和边界框回归。目标分类是指确定候选区域中是否存在目标,并将其分配到不同的类别中。边界框回归是指对候选区域进行微调,以更准确地框定目标的位置。
- 非极大值抑制:由于候选区域可能会有重叠,为了避免重复检测同一个目标,通常会使用非极大值抑制(NMS)来选择最佳的目标框。NMS会根据目标框的置信度和重叠度进行筛选,保留最有可能的目标框。
- 输出结果:最后,目标检测算法会输出检测到的目标框及其对应的类别标签和置信度。
4.当前目标检测存在问题与解决方案
目标检测是计算机视觉领域的一个核心任务,它旨在识别并定位图像中的各种目标。尽管目标检测技术已经取得了显著的进步,但仍然存在一些挑战性问题。以下是一些当前目标检测面临的问题以及可能的解决方案:
- 小目标检测难度大:
- 问题:在远距离拍摄或者分辨率较低的图像中,小目标的特征信息不足,难以被准确检测。
- 解决方案:可以通过设计更加敏感的特征提取网络,使用多尺度检测策略,或者利用GAN(生成对抗网络)来增强小目标的特征。
- 实时性能不足:
- 问题:高精度的目标检测模型往往计算复杂度高,难以满足实时应用的需求。
- 解决方案:可以通过模型剪枝、量化、知识蒸馏等模型压缩技术来减少计算量,或者设计轻量级网络结构来提高速度。
- 遮挡问题:
- 问题:当目标被遮挡时,检测性能会显著下降。
- 解决方案:可以采用注意力机制来强化关键特征,或者使用上下文信息辅助检测,以及通过3D建模来理解遮挡关系。
- 背景干扰和负样本问题:
- 问题:复杂的背景和负样本会导致误检。
- 解决方案:可以通过改进样本平衡策略,使用硬负样本挖掘,或者引入更鲁棒的损失函数来减少误检。
- 多尺度和多样性目标检测:
- 问题:不同尺度和外观多样性的目标检测是一个挑战。
- 解决方案:可以使用特征金字塔网络(FPN)来增强多尺度检测能力,或者通过数据增强和领域自适应技术来提高模型的泛化能力。
- 数据集偏差和标注错误:
- 问题:训练数据集可能存在偏差,标注也可能存在错误,这会影响模型性能。
- 解决方案:可以通过数据集增强、众包标注校验或者使用半监督学习和弱监督学习方法来减少这种影响。
- 跨域检测问题:
- 问题:模型在一个域上训练得很好,但在另一个域上性能下降。
- 解决方案:可以采用迁移学习和领域自适应技术来提高模型在不同域上的泛化能力。
- 计算资源限制:
- 问题:高性能的目标检测模型往往需要大量的计算资源。
- 解决方案:可以通过云计算平台提供计算资源,或者优化模型结构和算法来减少资源需求。
5.目标检测的常用数据集
- PASCAL VOC (Visual Object Classes):
- 包含20个目标类别,如人、动物、车辆和日常物品。
- 常用的版本有2007和2012,提供了训练集、验证集和测试集。
- MS COCO (Microsoft Common Objects in Context):
- 包含80个目标类别,图像来自日常场景,目标标注为实例分割形式。
- 每年都会举办挑战赛,是目标检测领域的一个重要基准。
- ImageNet:
- 虽然主要用于图像分类,但其中的ILSVRC(ImageNet Large Scale Visual Recognition Challenge)部分包含目标检测挑战。
- 包含数百个类别和数百万张图像。
- KITTI Vision Benchmark Suite:
- 专注于汽车自动驾驶场景,包含多种传感器数据。
- 目标检测任务包括车辆、行人等。
- Cityscapes:
- 针对城市街景的数据集,主要用于语义理解任务,包括目标检测。
- 包含50个城市的街景图像,重点在于车辆和行人。
- Open Images Dataset:
- 由Google发布,包含数百万张图像和数千个类别。
- 提供了大量的图像级别和物体级别的标注。
- WIDER FACE:
- 专注于面部检测,包含各种尺度、姿态和遮挡情况下的人脸。
- 图像来源于公共事件的照片。
- UAV123:
- 专为无人机视角下的目标检测设计,包含123个视频序列。
- 目标包括人、车辆等。
- DOTA (Dataset for Object deTection in Aerial images):
- 专注于航拍图像的目标检测,包含15个类别,如飞机、船只、运动场等。
- 图像分辨率高,目标尺寸多样。
- LVIS (Large Vocabulary Instance Segmentation):
- 包含更多类别的实例分割数据集,也可用于目标检测。
- 包含1200多个类别,注重长尾分布。
6.目标检测的评价指标
目标检测的评价指标用于衡量模型的性能。以下是一些基本概念和定义:
6.1 TP、TN、FP和FN
- TP (True Positives):正确检测到的正样本数量。
- TN (True Negatives):正确未检测到的负样本数量(在目标检测中不常用,因为通常不关心背景的分类)。
- FP (False Positives):错误检测到的正样本数量,即背景或其他类别被错误标记为目标类别。
- FN (False Negatives):未检测到的正样本数量,即目标类别被遗漏。
6.2 Precision和Recall
- Precision (精度):在所有检测到的正样本中,正确检测到的比例。
Precision = TP / (TP + FP) - Recall (召回率):在所有实际正样本中,正确检测到的比例。
Recall = TP / (TP + FN)
6.3 评价指标计算案例 假设我们有一个目标检测模型,用于检测图像中的猫。在一个测试集中,有以下结果:
- 模型检测到了10只猫,其中8只是正确的(TP=8),2只是错误的(FP=2)。
- 实际上,测试集中有12只猫,模型漏掉了4只(FN=4)。
那么,我们可以计算出:
- Precision = TP / (TP + FP) = 8 / (8 + 2) = 0.8
- Recall = TP / (TP + FN) = 8 / (8 + 4) = 0.6667
6.4 AP和mAP
- AP (Average Precision):对于单个类别,AP是在不同召回率水平下,精度的平均值。它可以通过绘制Precision-Recall曲线来计算,即曲线下面积。
- mAP (Mean Average Precision):当有多个类别时,mAP是所有类别AP的平均值。
6.5 [email protected]和[email protected]:0.95
- [email protected]:计算mAP时,使用IoU=0.5作为阈值。即只有当预测框和真实框的IoU大于等于0.5时,预测才被认为是正确的。
- [email protected]:0.95:这是一个更严格的评价指标,它计算IoU从0.5到0.95(以0.05为步长)的mAP的平均值。这意味着模型需要在多个IoU阈值下都表现良好才能获得高分。
7.IoU
7.1 IoU背景
IoU(Intersection over Union)是计算机视觉中用于评估目标检测模型性能的一个重要指标,特别是在边界框预测的准确性方面。
7.2 什么是IoU
IoU是一个衡量两个边界框重叠程度的指标。它是预测边界框和真实边界框交集面积与它们并集面积的比值。IoU的值介于0到1之间,值越高表示重叠程度越大。
7.3 IoU发展历程
IoU的概念随着时间发展,衍生出了多种变体,以解决标准IoU在某些情况下的局限性,如边界框不重叠或只有部分重叠的情况。
7.3.1 GIoU (Generalized IoU, CVPR2019)
GIoU在标准IoU的基础上进行了扩展,即使两个边界框不重叠时也能提供一个有意义的值。GIoU考虑了边界框之间的包含关系和距离。
7.3.2 DIoU (Distance-IoU, AAAI2020)
DIoU在IoU的基础上加入了中心点距离的度量,以解决标准IoU在评估非重叠边界框时的不足。
7.3.3 CIoU (Complete IoU, AAAI2020)
CIoU进一步改进了DIoU,加入了长宽比的一致性度量,使得CIoU不仅考虑了中心点距离,还考虑了形状相似性。
7.3.4 EIoU (Enhanced IoU, arXiv2021)
EIoU是对GIoU的改进,它通过引入额外的度量来增强GIoU的性能。
7.3.5 AIoU (Attention IoU, NeurIPS2021)
AIoU是一种新的IoU变体,它使用注意力机制来更好地捕捉边界框之间的相互关系。
7.3.6 SIoU (Scale-Invariant IoU, arXiv2022)
SIoU是最新的IoU变体之一,它考虑了尺度不变性,以解决在不同尺度下边界框评估的问题。
8.NMS
8.1 什么是NMS
NMS(Non-Maximum Suppression)是一种用于消除多余边界框的技术,通常在目标检测任务中使用,以保留最佳的边界框。
8.2 NMS算法流程
- 对所有检测到的边界框按照置信度排序。
- 选择置信度最高的边界框,并移除所有与它重叠度(IoU)高于某个阈值的边界框。
- 重复上述过程,直到所有边界框都被处理。
8.3 NMS过程图例
8.3.1 单类别例子
- 在单类别检测中,NMS会移除与最高置信度边界框重叠度过高的其他边界框。
8.3.2 多类别例子
- 在多类别检测中,NMS通常会对每个类别独立执行,以避免不同类别之间的边界框相互影响。
8.4 Soft-NMS (ICCV2017)
Soft-NMS是NMS的一个变体,它不是直接移除与最高置信度边界框重叠度高的边界框,而是降低它们的置信度。
8.5 Weighted-NMS (ICMEW2017)
Weighted-NMS在移除重叠边界框时,会根据它们的置信度和重叠度计算一个权重,然后用这个权重来更新保留下来的边界框。
8.6 分类置信度优先
这种方法优先考虑分类置信度高的边界框,以提高检测的准确性。
8.7 IOU-Guided NMS (ECCV2018)
IOU-Guided NMS在标准NMS的基础上加入了IoU信息,以更精确地执行边界框的抑制。
8.8 Softer NMS (CVPR2019)
Softer NMS是Soft-NMS的改进版本,它进一步优化了边界框的置信度调整策略。
8.9 Adaptive NMS (CVPR2019)
Adaptive NMS根据检测场景的密集程度自适应地调整NMS的阈值。
8.10 DIoU-NMS (AAAI2020)
DIoU-NMS是在NMS中加入DIoU计算,以更好地考虑边界框之间的几何关系。
8.11 NMS总结
NMS及其变体是目标检测中不可或缺的后处理步骤,它们在提高检测性能方面起着关键作用。随着研究的深入,NMS的新变体不断被提出,以解决特定的问题和挑战。
第6篇模型优化方法及思路
1. 一个合适的梯度下降优化算法
1.1 梯度下降法的变形形式 1.1.1 批梯度下降法 (Batch Gradient Descent)
- 在每次更新中使用所有的样本来计算梯度。
1.1.2 随机梯度下降 (Stochastic Gradient Descent, SGD)
- 在每次更新中随机选择一个样本来计算梯度。
1.1.3 小批量梯度下降法 (Mini-batch Gradient Descent)
- 在每次更新中使用一小批样本来计算梯度。
1.2 梯度下降优化算法 1.2.1 动量法 (Momentum)
- 为梯度下降引入惯性,帮助加速SGD在相关方向上的收敛,并抑制震荡。
1.2.2 Nesterov 加速梯度 (Nesterov Accelerated Gradient, NAG)
- 在动量法的基础上进行改进,提前在动量方向上进行梯度计算。
1.2.3 Adagrad
- 自适应地为不同的参数分配不同的学习率。
1.2.4 Adadelta
- 是Adagrad的一个改进版本,减少了其学习率递减的激进性。
1.2.5 RMSprop
- 修正Adagrad学习率急剧下降的问题,通过引入衰减系数来限制历史信息的无限积累。
1.2.6 Adam (Adaptive Moment Estimation)
- 结合了Momentum和RMSprop的优点,计算每个参数的自适应学习率。
1.2.7 算法可视化
- 通过可视化不同优化算法的优化路径,可以更直观地理解它们的行为和性能。
1.2.8 选择使用哪种优化算法?
- 选择优化算法通常基于问题的具体情况,如数据的大小、模型的复杂性、计算资源等。Adam由于其稳定性和快速收敛通常是一个不错的首选。
1.3 优化SGD的其他策略 1.3.1 数据集的洗牌和课程学习
- 通过随机打乱数据来防止模型学习到数据的顺序,课程学习是一种先学习简单样本再学习复杂样本的策略。
1.3.2 批量归一化 (Batch Normalization)
- 通过对每个小批量数据进行标准化处理,加速训练过程。
1.3.3 Early stopping
- 为了防止过拟合,当验证集上的性能不再提升时停止训练。
1.3.4 梯度噪音
- 向梯度中添加噪声,有助于提高模型的泛化能力。
1.4 总结
- 选择合适的优化算法和策略对于训练高效、高性能的模型至关重要。
2. 训练误差和泛化误差
- 训练误差:模型在训练数据上的误差,反映了模型对训练数据的拟合程度。
- 泛化误差:模型在新数据上的误差,反映了模型的泛化能力。
3. 有哪些改善模型的思路
3.1 数据角度 3.1.1 数据增强是什么?
- 数据增强是通过对原始数据进行变换生成新数据的技术,以此来增加数据多样性,提高模型的泛化能力。
3.1.2 离线增强与在线增强
- 离线增强:提前生成增强数据集。
- 在线增强:在模型训练过程中实时生成增强数据。
3.1.3 常见数据增强方式
- 包括旋转、翻转、缩放、裁剪、颜色变换等。
3.1.4 数据增强的限制
- 数据增强不能引入错误的标签,且应保持数据的本质特征。
3.2 模型角度 3.2.1 什么是基线 (baseline)?
- 基线是一个简单的模型,通常用于为特定任务提供一个性能参考点。
3.2.2 如何选择一个合适的基线? 3.2.2.1 从硬件性能角度考虑
- 根据可用的计算资源选择合适的模型大小。
3.2.2.2 从训练成本角度考虑
- 考虑模型训练所需的时间和经济成本。
3.2.2.3 从评价指标角度考虑
- 选择能够在关键指标上表现良好的模型。
3.2.2.4 从代码开源角度考虑
- 选择有良好社区支持和文档的模型。
3.3 调参优化角度 3.3.1 学习率策略角度
- 选择合适的学习率和调整策略,如学习率衰减。
3.3.2 数据增强参数
- 调整数据增强的参数以获得最佳效果。
3.4 训练角度 3.4.1 加大训练轮数
- 在不过拟合的前提下,增加训练的轮数。
3.4.2 标签平滑
- 通过平滑标签来防止模型对某些类别过于自信。
3.4.3 多尺度训练
- 在不同尺度上训练模型,提高模型的尺度不变性。
3.4.4 是否使用权重
- 使用预训练权重或者在训练过程中调整权重分配。
第7篇模型超参数调整策略
模型超参数调整是机器学习和深度学习中的一个重要环节,它涉及到选择一组能够使模型达到最佳性能的超参数。以下是一些常用的超参数调整策略:
1. 手动调整
这是最基本的调整策略,依赖于研究者的经验和直觉。研究者根据模型在验证集上的表现手动调整超参数。这种方法虽然费时,但可以帮助研究者更深入地理解模型和数据。
2. 网格搜索 (Grid Search)
网格搜索是一种穷举搜索方法,它会系统地遍历多种超参数的组合。对于每一组超参数,模型都会被训练并评估其性能。最终选择表现最好的超参数组合。网格搜索简单直观,但当超参数空间很大时,它可能会非常耗时。
3. 随机搜索 (Random Search)
随机搜索不像网格搜索那样尝试每一种可能的组合,而是在超参数空间中随机选择组合。研究表明,在很多情况下,随机搜索比网格搜索更高效,因为它能够探索更广泛的空间,并且不会浪费时间在不重要的超参数上。
4. 贝叶斯优化 (Bayesian Optimization)
贝叶斯优化是一种基于概率模型的优化方法,它利用先前评估的结果来选择下一组超参数,以期望找到性能提升。贝叶斯优化试图平衡探索(尝试新的、不确定的超参数)和利用(使用已知提供好结果的超参数)。
5. 超参数优化算法
- 遗传算法 (Genetic Algorithms):通过模拟自然选择的过程来搜索超参数空间。
- 粒子群优化 (Particle Swarm Optimization, PSO):模拟鸟群狩猎行为的算法,通过群体合作来搜索最优解。
6. 基于模型的超参数优化
- Hyperband:一种基于资源分配和早期停止的方法,它会动态分配资源给更有前景的配置。
- BOHB (Bayesian Optimization and Hyperband):结合了Hyperband的快速性和贝叶斯优化的精确性。
7. 自动化机器学习 (AutoML)
自动化机器学习工具,如Google的AutoML、H2O AutoML和Auto-sklearn,可以自动进行超参数搜索和模型选择。
8. 调整策略
- 学习率:
- 概念:学习率定义了在每次迭代中更新模型权重时所采用的步长大小。
- 作用:它控制了模型学习的速度。太高可能导致模型无法收敛,太低则可能导致训练过程过慢或陷入局部最小值。
- 调整方案:可以使用网格搜索或随机搜索来找到一个合适的学习率范围,也可以使用学习率衰减或自适应学习率算法。
- 调整结果:合适的学习率可以帮助模型更快地收敛并提高最终性能。
- 早停法 (Early Stopping):
- 概念:一种避免过拟合的策略,通过监控验证集的性能来决定何时停止训练。
- 作用:当模型在验证集上的性能不再提升时,停止训练可以防止模型在训练集上过度拟合。
- 调整方案:设置一个“耐心”参数,即在验证集上性能没有提升的连续epoch数,达到该数值后停止训练。
- 调整结果:可以得到泛化能力更强的模型,并减少训练时间。
- 学习率衰减:
- 概念:随着训练的进行,逐步减少学习率的策略。
- 作用:在训练初期使用较大的学习率以快速进展,在训练后期使用较小的学习率以细化模型参数。
- 调整方案:可以设置一个衰减系数或者使用预定的衰减时间表,也可以根据模型的验证集性能动态调整学习率。
- 调整结果:有助于模型在接近最优解时更精细地调整权重,提高模型的最终性能。
- 正则化项:
- 概念:在损失函数中加入一个额外的项,以惩罚模型的复杂度。
- 作用:L1正则化倾向于产生稀疏权重矩阵,L2正则化则倾向于限制权重的大小,防止过拟合。
- 调整方案:通过交叉验证来选择合适的正则化强度(即正则化项的系数)。
- 调整结果:适当的正则化可以提高模型的泛化能力,减少过拟合的风险。
- 批量大小 (Batch Size):
- 概念:在每次迭代中用于计算梯度并更新权重的样本数量。
- 作用:影响模型的收敛速度和内存使用量。较大的批量可以提供更稳定的梯度估计,但可能增加内存需求。
- 调整方案:根据可用的内存资源和模型的收敛行为来选择批量大小,可能需要在训练速度和内存使用之间做出权衡。
- 调整结果:合适的批量大小可以加快训练速度,同时保持模型性能。
- 网络架构相关参数:
- 概念:包括层数、每层的单元数或卷积核的大小等。
- 作用:决定了模型的容量,即模型拟合复杂数据的能力。
- 调整方案:通常需要基于问题的复杂性和可用数据的量来实验性地确定这些参数。
- 调整结果:适当的网络架构可以提高模型的性能,避免过拟合或欠拟合。
9. 总结
超参数调整是一个迭代的过程,通常需要多次尝试和验证。在实际操作中,可以结合多种策略,如先使用随机搜索找到一个大致的范围,然后用网格搜索进行细化。贝叶斯优化和AutoML等高级方法可以进一步提高搜索效率。重要的是要记录每次实验的配置和结果,以便于分析和比较不同的超参数对模型性能的影响。
第8篇模型压缩
模型压缩是指通过一系列技术手段来减小深度学习模型的大小,从而减少模型在存储和计算资源上的需求。模型压缩的目标是在尽量保持模型性能的前提下,减少模型的存储空间和计算复杂度。
常见的模型压缩方法包括:
- 参数剪枝(Pruning):通过删除模型中冗余的参数来减小模型的大小。剪枝方法可以基于权重、通道或层级进行,可以使用稀疏矩阵表示来存储剪枝后的模型。
- 量化(Quantization):将模型中的浮点数参数转换为低精度的定点数或整数,从而减小模型的存储需求。常见的量化方法包括权重量化和激活量化。
- 低秩分解(Low-rank Decomposition):通过将模型中的卷积层或全连接层分解为多个较小的矩阵乘法操作,从而减小模型的计算复杂度和存储需求。
- 知识蒸馏(Knowledge Distillation):通过使用一个较大的教师模型的输出作为目标,训练一个较小的学生模型,从而减小模型的大小。
- 网络剪枝(Network Pruning):通过删除模型中的冗余连接或层级来减小模型的大小和计算复杂度。
这些方法可以单独使用,也可以结合使用,以达到更好的压缩效果。模型压缩可以帮助在资源受限的设备上部署更大的模型,或者加速模型的推理过程。
8.1 参数剪枝
**参数剪枝(Pruning)**是一种模型压缩方法,通过删除模型中冗余的参数来减小模型的大小。参数剪枝可以基于权重、通道或层级进行。
基于权重的参数剪枝方法通过删除模型中绝对值较小的权重来减小模型的大小。这背后的假设是,这些权重对模型的性能影响较小,因此可以被删除而不会对模型的性能产生显著影响。
基于通道的参数剪枝方法通过删除模型中冗余的通道来减小模型的大小。这背后的假设是,有些通道对模型的性能影响较小,因此可以被删除而不会对模型的性能产生显著影响。
基于层级的参数剪枝方法通过删除模型中冗余的层级来减小模型的大小。这背后的假设是,有些层级对模型的性能影响较小,因此可以被删除而不会对模型的性能产生显著影响。
参数剪枝的方法有很多,下面介绍几种常用的方法:
- L1正则化:L1正则化是一种正则化方法,可以惩罚模型中权重的绝对值。通过使用L1正则化,可以使模型中权重的绝对值变小,从而实现参数剪枝。
- L2正则化:L2正则化是一种正则化方法,可以惩罚模型中权重的平方值。通过使用L2正则化,可以使模型中权重的平方值变小,从而实现参数剪枝。
- 剪枝后重新训练:剪枝后重新训练是一种参数剪枝方法,它首先使用上述方法之一对模型进行剪枝,然后对剪枝后的模型进行重新训练。重新训练可以帮助模型适应剪枝后的结构,从而保持模型的性能。
- 渐进式剪枝:渐进式剪枝是一种参数剪枝方法,它通过迭代地剪枝和重新训练模型来实现参数剪枝。渐进式剪枝可以帮助模型更好地适应剪枝后的结构,从而保持模型的性能。
参数剪枝是一种有效的模型压缩方法,可以显著减小模型的大小,而不会对模型的性能产生显著影响。参数剪枝可以帮助在资源受限的设备上部署更大的模型,或者加速模型的推理过程。
8.2 量化
**量化(Quantization)**是一种模型压缩方法,将模型中的浮点数参数转换为低精度的定点数或整数,从而减小模型的存储需求。量化可以分为权重量化和激活量化。
权重量化是指将模型中的浮点数权重转换为低精度的定点数或整数。权重量化可以减小模型的存储需求,并可以加速模型的推理过程。
激活量化是指将模型中的浮点数激活值转换为低精度的定点数或整数。激活量化可以减小模型的存储需求,并可以加速模型的推理过程。
量化的主要方法有:
- 均匀量化:均匀量化是一种简单的量化方法,它将浮点数参数或激活值均匀地映射到低精度的定点数或整数。均匀量化可以很容易地实现,但量化误差可能较大。
- 非均匀量化:非均匀量化是一种更复杂的量化方法,它根据浮点数参数或激活值的重要性来分配量化比特。非均匀量化可以减少量化误差,但实现起来也更复杂。
量化是一种有效的模型压缩方法,可以显著减小模型的大小,而不会对模型的性能产生显著影响。量化可以帮助在资源受限的设备上部署更大的模型,或者加速模型的推理过程。
下面是一些常用的量化方法:
- 二值化(Binaryzation):二值化是一种极端的量化方法,它将浮点数参数或激活值转换为二进制值(0或1)。二值化可以显著减小模型的大小,但也会导致模型的性能下降。
- 比特宽度自适应量化(Bit-width Adaptive Quantization):比特宽度自适应量化是一种量化方法,它根据浮点数参数或激活值的重要性来分配量化比特。比特宽度自适应量化可以减少量化误差,并可以保持模型的性能。
- 张量分解量化(Tensor Decomposition Quantization):张量分解量化是一种量化方法,它将浮点数参数或激活值分解为多个低秩张量,然后对这些低秩张量进行量化。张量分解量化可以减少量化误差,并可以保持模型的性能。
量化是一种有效的模型压缩方法,可以显著减小模型的大小,而不会对模型的性能产生显著影响。量化可以帮助在资源受限的设备上部署更大的模型,或者加速模型的推理过程。
8.3 低秩分解
**低秩分解(Low-rank Decomposition)**是一种数学方法,它将一个矩阵分解为多个较小的矩阵乘法操作。低秩分解可以用于模型压缩,通过将模型中的卷积层或全连接层分解为多个较小的矩阵乘法操作,从而减小模型的计算复杂度和存储需求。
低秩分解的方法有很多,下面介绍几种常用的方法:
- 奇异值分解(Singular Value Decomposition, SVD):SVD是一种经典的低秩分解方法,它将一个矩阵分解为三个矩阵的乘积:一个正交矩阵、一个对角矩阵和一个正交矩阵的转置。SVD可以用于任何矩阵的低秩分解,但其计算复杂度较高。
- 截断奇异值分解(Truncated Singular Value Decomposition, TSVD):TSVD是一种SVD的变体,它通过截断SVD中的小奇异值来降低计算复杂度。TSVD可以用于模型压缩,但其分解精度可能不如SVD。
- 核范数正则化(Nuclear Norm Regularization):核范数正则化是一种正则化方法,它惩罚矩阵的核范数。核范数正则化可以使矩阵的秩变小,从而实现低秩分解。核范数正则化可以用于模型压缩,但其分解精度可能不如SVD或TSVD。
低秩分解是一种有效的模型压缩方法,可以显著减小模型的计算复杂度和存储需求,而不会对模型的性能产生显著影响。低秩分解可以帮助在资源受限的设备上部署更大的模型,或者加速模型的推理过程。
下面是一些常用的低秩分解方法:
- 张量分解(Tensor Decomposition):张量分解是一种低秩分解方法,它将一个张量分解为多个较小的张量乘法操作。张量分解可以用于模型压缩,通过将模型中的卷积层或全连接层分解为多个较小的张量乘法操作,从而减小模型的计算复杂度和存储需求。
- 矩阵分解(Matrix Decomposition):矩阵分解是一种低秩分解方法,它将一个矩阵分解为多个较小的矩阵乘法操作。矩阵分解可以用于模型压缩,通过将模型中的卷积层或全连接层分解为多个较小的矩阵乘法操作,从而减小模型的计算复杂度和存储需求。
- 核范数正则化(Nuclear Norm Regularization):核范数正则化是一种正则化方法,它惩罚矩阵的核范数。核范数正则化可以使矩阵的秩变小,从而实现低秩分解。核范数正则化可以用于模型压缩,通过惩罚模型中卷积层或全连接层的核范数来减小模型的计算复杂度和存储需求。
低秩分解是一种有效的模型压缩方法,可以显著减小模型的计算复杂度和存储需求,而不会对模型的性能产生显著影响。低秩分解可以帮助在资源受限的设备上部署更大的模型,或者加速模型的推理过程。
8.4 知识蒸馏
**知识蒸馏(Knowledge Distillation)**是一种模型压缩方法,通过使用一个较大的教师模型的输出作为目标,训练一个较小的学生模型,从而减小模型的大小。知识蒸馏背后的假设是,教师模型已经学习到了丰富的知识,这些知识可以帮助学生模型学习到更好的表示。
知识蒸馏的方法有很多,下面介绍几种常用的方法:
- 软目标蒸馏(Soft Target Distillation):软目标蒸馏是一种知识蒸馏方法,它使用教师模型的输出作为学生模型的软目标。软目标蒸馏可以帮助学生模型学习到教师模型的知识,同时保持学生模型的灵活性。
- 硬目标蒸馏(Hard Target Distillation):硬目标蒸馏是一种知识蒸馏方法,它使用教师模型的输出作为学生模型的硬目标。硬目标蒸馏可以帮助学生模型学习到教师模型的知识,但可能会导致学生模型的灵活性降低。
- 特征蒸馏(Feature Distillation):特征蒸馏是一种知识蒸馏方法,它使用教师模型的中间特征作为学生模型的监督信号。特征蒸馏可以帮助学生模型学习到教师模型的知识,同时保持学生模型的灵活性。
知识蒸馏是一种有效的模型压缩方法,可以显著减小模型的大小,而不会对模型的性能产生显著影响。知识蒸馏可以帮助在资源受限的设备上部署更大的模型,或者加速模型的推理过程。
下面是一些常用的知识蒸馏方法:
- 教师-学生模型蒸馏(Teacher-Student Model Distillation):教师-学生模型蒸馏是一种知识蒸馏方法,它使用一个较大的教师模型来训练一个较小的学生模型。教师模型的输出作为学生模型的软目标或硬目标,帮助学生模型学习到教师模型的知识。
- 中间特征蒸馏(Intermediate Feature Distillation):中间特征蒸馏是一种知识蒸馏方法,它使用教师模型的中间特征作为学生模型的监督信号。中间特征蒸馏可以帮助学生模型学习到教师模型的知识,同时保持学生模型的灵活性。
- 注意力蒸馏(Attention Distillation):注意力蒸馏是一种知识蒸馏方法,它使用教师模型的注意力机制来指导学生模型的注意力机制。注意力蒸馏可以帮助学生模型学习到教师模型的知识,同时保持学生模型的灵活性。
知识蒸馏是一种有效的模型压缩方法,可以显著减小模型的大小,而不会对模型的性能产生显著影响。知识蒸馏可以帮助在资源受限的设备上部署更大的模型,或者加速模型的推理过程。
8.5 网络剪枝
**网络剪枝(Network Pruning)**是一种模型压缩方法,通过删除模型中的冗余连接或层级来减小模型的大小和计算复杂度。网络剪枝背后的假设是,有些连接或层级对模型的性能影响较小,因此可以被删除而不会对模型的性能产生显著影响。
网络剪枝的方法有很多,下面介绍几种常用的方法:
- 权重剪枝(Weight Pruning):权重剪枝是一种网络剪枝方法,它通过删除模型中绝对值较小的权重来减小模型的大小。权重剪枝可以很容易地实现,但可能会导致模型的性能下降。
- 通道剪枝(Channel Pruning):通道剪枝是一种网络剪枝方法,它通过删除模型中冗余的通道来减小模型的大小。通道剪枝可以帮助减小模型的计算复杂度,但可能会导致模型的性能下降。
- 层级剪枝(Layer Pruning):层级剪枝是一种网络剪枝方法,它通过删除模型中冗余的层级来减小模型的大小。层级剪枝可以帮助减小模型的计算复杂度,但可能会导致模型的性能下降。
网络剪枝是一种有效的模型压缩方法,可以显著减小模型的大小和计算复杂度,而不会对模型的性能产生显著影响。网络剪枝可以帮助在资源受限的设备上部署更大的模型,或者加速模型的推理过程。
下面是一些常用的网络剪枝方法:
- L1正则化(L1 Regularization):L1正则化是一种正则化方法,可以惩罚模型中权重的绝对值。通过使用L1正则化,可以使模型中权重的绝对值变小,从而实现网络剪枝。
- L2正则化(L2 Regularization):L2正则化是一种正则化方法,可以惩罚模型中权重的平方值。通过使用L2正则化,可以使模型中权重的平方值变小,从而实现网络剪枝。
- 剪枝后重新训练(Pruning-and-Retraining):剪枝后重新训练是一种网络剪枝方法,它首先使用上述方法之一对模型进行剪枝,然后对剪枝后的模型进行重新训练。重新训练可以帮助模型适应剪枝后的结构,从而保持模型的性能。
- 渐进式剪枝(Progressive Pruning):渐进式剪枝是一种网络剪枝方法,它通过迭代地剪枝和重新训练模型来实现网络剪枝。渐进式剪枝可以帮助模型更好地适应剪枝后的结构,从而保持模型的性能。
网络剪枝是一种有效的模型压缩方法,可以显著减小模型的大小和计算复杂度,而不会对模型的性能产生显著影响。网络剪枝可以帮助在资源受限的设备上部署更大的模型,或者加速模型的推理过程。
参考
1、https://mlnotebook.github.io/post/CNN1/
2、