Bootstrap

分治（算法七）

分治可分为两种：快速排序与归并排序中的分治方法

 快排分治

快排简介

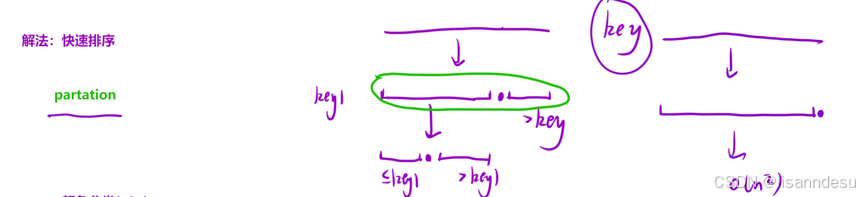
传统分治快排，数组分为两部分，左边小于等于key，右边大于key

但当数组所有元素都一样时，此算法时间复杂度为O(N^2)：

解决方案：数组分三块思想（同《颜色分类》一题）：

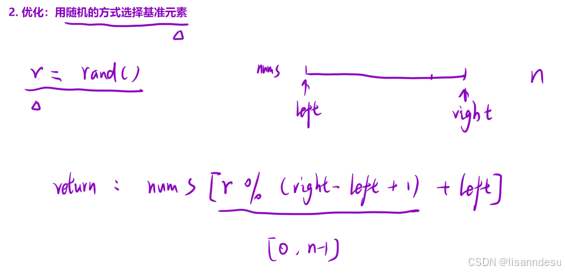
优化：随机选择key（可使时间复杂度趋近NlogN）：

 解题代码见第二题《快速排序》

1.颜色分类

link：75. 颜色分类 - 力扣（LeetCode）

思路

本题体现了数组划分思想， 为分支/快排打基础

类似移动零，但是三指针

code：

class Solution {
public:
    void sortColors(vector<int>& nums) {
        int sz = nums.size();
        for(int left = -1, right = sz, cur = 0; cur < right; )
        {
            if(nums[cur] == 0)
            {
                swap(nums[++left], nums[cur++]);
            }
            else if(nums[cur] == 1)
            {
                ++cur;
            }
            else if(nums[cur] == 2)
            {
                swap(nums[cur], nums[--right]);//cur左边已排序，可以++cur， 但右边没排序, cur不可++
            }
        }
    }
};

2.快速排序

link:912. 排序数组 - 力扣（LeetCode）

思路：

        颜色分类(数组分三类）

        分治

code：

class Solution {
public:
    //数组分三块 + 随机选择key
    vector<int> sortArray(vector<int>& nums) {
        qsort(nums, 0, nums.size()-1); 
        return nums;
    }

    void qsort(vector<int>& nums, int bgn, int ed)
    {
        if(bgn >= ed) return;
        int left = bgn, right = ed;
        int key = randomKey(nums, bgn, ed);
        --left;
        ++right;
        for(int cur = left+1; cur < right;)
        {
            if(nums[cur] < key)
            {
                swap(nums[cur++], nums[++left]);
            }
            else if(nums[cur] == key)
            {
                cur++;
            }
            else //(nums[cur] > key)
            {
                swap(nums[cur], nums[--right]);
            }
        }
        qsort(nums, bgn, left);
        qsort(nums, right, ed);
    }

    int randomKey(vector<int>& nums, int left, int right)
    {
        int idx =left + rand() % (right - left + 1);
        return nums[idx];
    }
};

        

3.数组中第k个最大元素

link：215. 数组中的第K个最大元素 - 力扣（LeetCode）

思路：

        数组分三块 + 单调性

code

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        //数组分三块 快速排序法
        return qsort(nums, 0, nums.size()-1, k);
    }
    int qsort(vector<int>& nums, int bgn, int ed, int k)
    {
        int left = bgn - 1, right = ed + 1;
        int key = randomKey(nums, bgn, ed);
        for(int cur = bgn; cur < right; )
        {
            if(nums[cur] < key) swap(nums[cur++], nums[++left]);
            else if(nums[cur] == key) cur++;
            else swap(nums[cur], nums[--right]);
        }
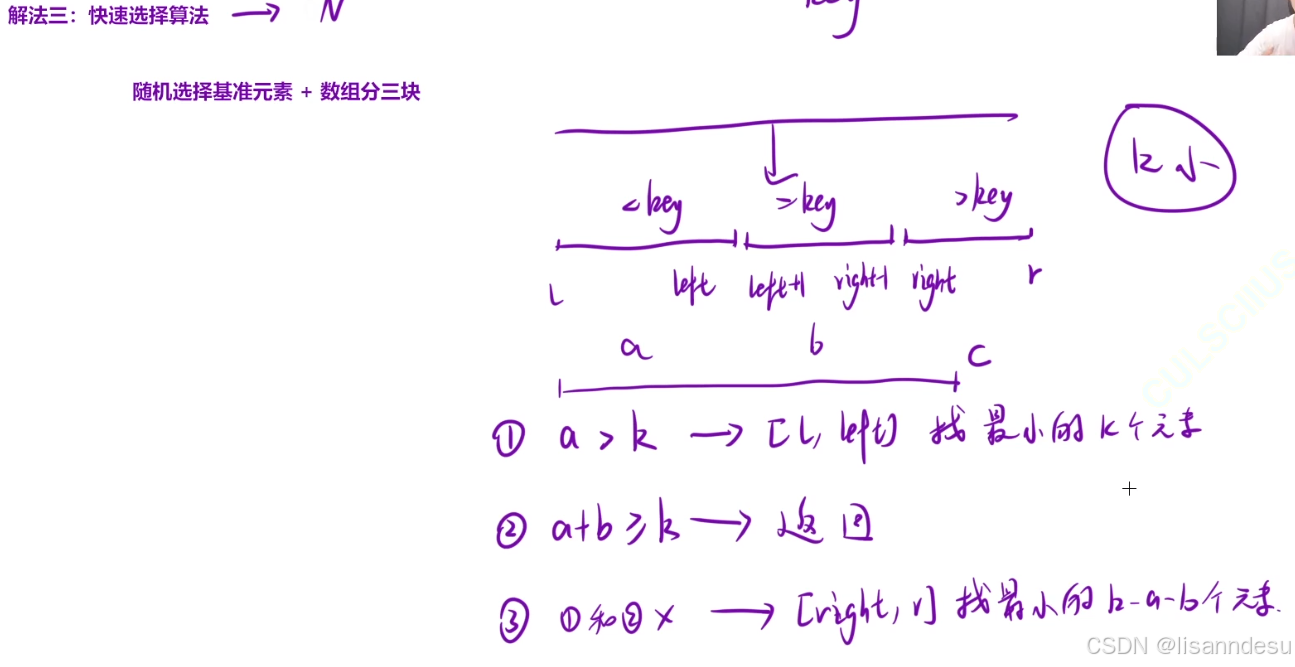
        int c = ed - right + 1, b = right - left - 1;
        if(k <= c) return qsort(nums, right, ed, k);
        else if(k > c && k <= b + c) return key;
        else return qsort(nums, bgn, left, k-(c+b));
    }
    
    int randomKey(vector<int>& nums, int left, int right)
    {
        size_t idx = rand() % (right - left + 1) + left;
        return nums[idx];
    }
};

4.最小K个数

link：面试题 17.14. 最小K个数 - 力扣（LeetCode）

思路：

        数组分三块 + 单调性

快排求前k小为什么能O(N)：没要求答案有序，可利用数组分三块算法处理后的数组的单调性

code

class Solution {
public:
    vector<int> smallestK(vector<int>& arr, int k) {
        qsort(arr, 0, arr.size()-1, k);
        return {arr.begin(), arr.begin()+k};
    }
    
    void qsort(vector<int>& nums, int bgn, int ed, int k)
    {
        if(bgn >= ed) return;
        int key = randomKey(nums, bgn, ed);
        int left = bgn - 1, right = ed + 1;
        for(int cur = bgn; cur < right;)
        {
            if(nums[cur] < key) swap(nums[cur++], nums[++left]);
            else if (nums[cur] == key) cur++;
            else swap(nums[--right], nums[cur]);
        }
        int a = left - bgn + 1, b = right - left - 1;
        if(k <= a) 
        {
            qsort(nums, bgn, left, k);
            return ;
        }
        if(k <= a + b) return;
        else
        {
            qsort(nums, right, ed, k - (a + b));
        }
    }

    int randomKey(vector<int>& nums, int bgn, int ed)
    {
        int idx = bgn + rand() % (ed - bgn + 1);
        return nums[idx];
    }
};

 归并分治

要理解归并排序原理， 就要从下向上看，因为下层先有序，上层后有序（当bgn==ed时，nums[bgn:end]必有序)

1.排序数组

link：912. 排序数组 - 力扣（LeetCode）

思路

        归并排序

code

class Solution {
public:
    vector<int> tmp;
    vector<int> sortArray(vector<int>& nums) {
        // 归并排序
        tmp.resize(nums.size());
        merge(nums, 0, nums.size()-1);
        return nums;
    }
    
    void merge(vector<int>& nums, int bgn, int ed)
    {
        if(bgn >= ed) return;
        int mid = (bgn + ed) >> 1;
        //划分排序
        merge(nums, bgn, mid);
        merge(nums, mid+1, ed);
        // 合并
        int p1 = bgn, p2 =mid + 1, cur = 0;
        while(p1 <= mid && p2 <= ed)
        {
            tmp[cur++] = nums[p1] < nums[p2] ? nums[p1++] : nums[p2++];
        }
        while(p1 <= mid)
        {
            tmp[cur++] = nums[p1++];
        }
        while(p2 <= ed)
        {
            tmp[cur++] = nums[p2++];
        }
        // 还原
        for(int i = bgn; i <= ed; i++)
        {
            nums[i] = tmp[i-bgn];
        }
    }
};

2.交易逆序对的总数

link:LCR 170. 交易逆序对的总数 - 力扣（LeetCode）

思路：

        分治 + 归并排序 + 滑动窗口

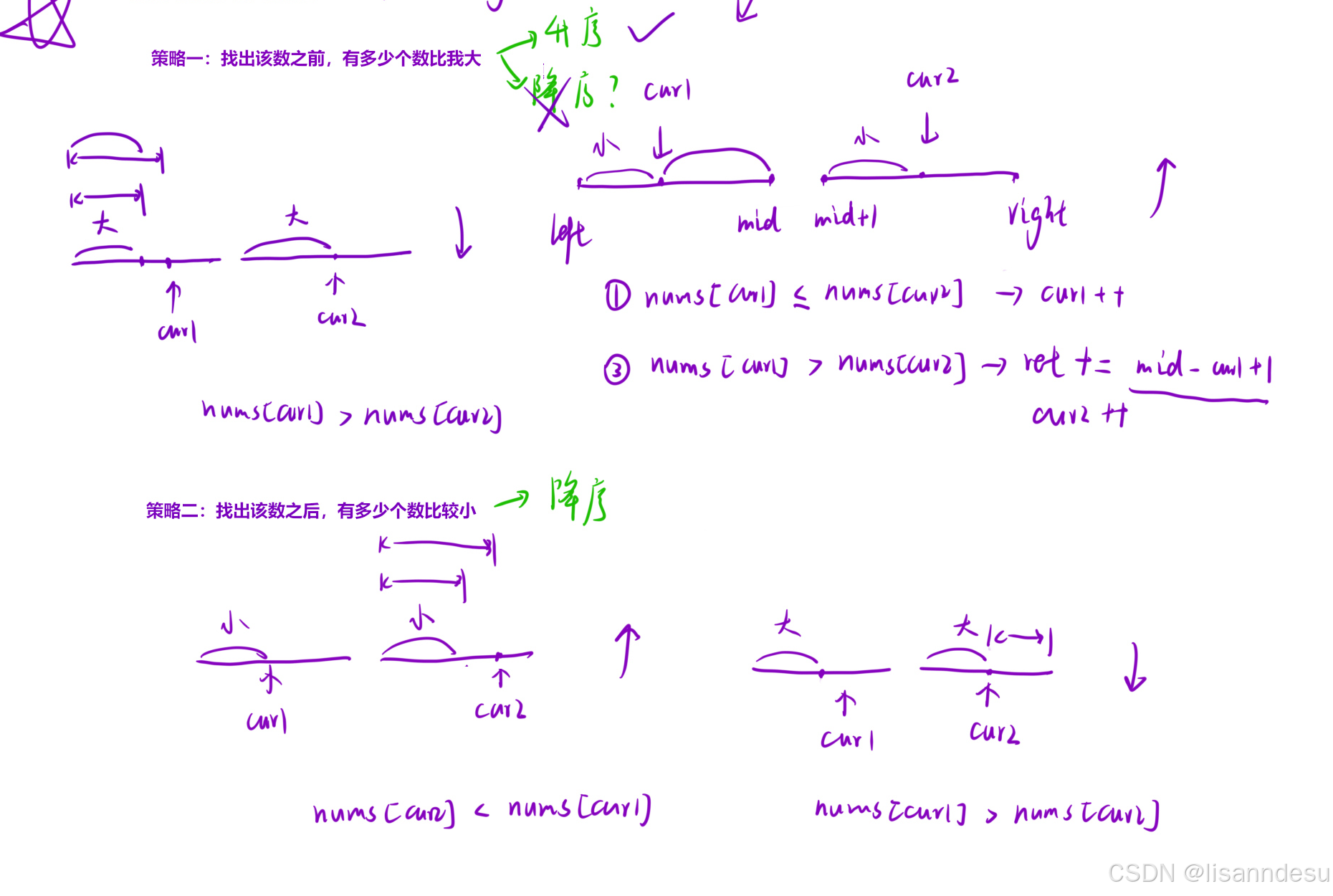
        使用策略一，在归并排序基础上稍加改动即可

两个策略：cur1, cur2以归并排序逻辑++前提下, 只有策略一二能同时解决本问题

code

class Solution {
public:
    vector<int> tmp;
    int reversePairs(vector<int>& record) {
        // 分治 + 滑动窗口
        tmp.resize(record.size());
        int ans = merge(record, 0, record.size()-1);
        return ans;
    }

    int merge(vector<int> &record, int bgn, int ed)
    {
        if(bgn >= ed) return 0;
        int ans = 0;
        // 左右分别各自组合
        int mid = (bgn + ed) >> 1;
        ans += merge(record, bgn, mid);
        ans += merge(record, mid + 1, ed);
        // 排序 + 左右组合 
        // 策略一：升序， 左边固定不动，找右面第一个比固定数大的
        int p1 = bgn, p2 = mid + 1, idx = 0;
        while(p1 <= mid && p2 <= ed) 
        {
            if(record[p1] <= record[p2])
            {// [mid + 1, p2 - 1]都比p1小
                ans += ((p2-1) - (mid+1) + 1);
                tmp[idx++] = record[p1++];
            }
            else tmp[idx++] = record[p2++];
        }
        // if(p1 != mid) // [p1, mid], [mid+1, ed]任意组合都满足条件
        ans += (mid - p1 + 1) * (ed - mid);
        while(p1 <= mid) tmp[idx++] = record[p1++];
        while(p2 <= ed) tmp[idx++] = record[p2++];
        for(int i = bgn; i <= ed; i++)
        {
            record[i] = tmp[i - bgn];
        }
        return ans;
    }
};

3.计算右侧小于当前元素的个数

link:315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）

思路：

        策略二

        分治-归并-排序，基本类似上一题

code

class Solution {
public:
    vector<int> numsTmp;
    vector<int> indexTmp;
    vector<int> index;
    vector<int> ans;
    // nums变化，就要更新index
    // numsTmp变化， 就要更新indexTmp
    vector<int> countSmaller(vector<int>& nums) {
        // 分治-归并-策略二
        // 降序-固定左边看右边， 找右边第一个比固定数小的元素
        numsTmp.resize(nums.size());
        indexTmp.resize(nums.size());
        index.resize(nums.size());
        ans.resize(nums.size());
        // init index[]
        for(int i = 0; i < index.size(); i++)
        {
            index[i] = i;
        }
        mergeSort(nums, 0, nums.size()-1);
        return ans;
    }

    void mergeSort(vector<int>& nums, int bgn, int ed)
    {
        if(bgn >= ed) return;
        // 左右分别排序
        int mid = (bgn + ed) >> 1;
        mergeSort(nums, bgn, mid);
        mergeSort(nums, mid + 1, ed);

        // 合并
        int p1 = bgn, p2 = mid + 1, idx = bgn;
        while(p1 <= mid && p2 <= ed)
        {
            if(nums[p1] <= nums[p2])//判断
            {
                numsTmp[idx] = nums[p2];
                indexTmp[idx] = index[p2];
                idx++;p2++;
            }
            else// nums[p2, ed]都比nums[p1]小
            {
                ans[index[p1]] += ed - p2 + 1;
                numsTmp[idx] = nums[p1];
                indexTmp[idx] = index[p1];
                idx++;p1++;
            }
        }
        while(p1 <= mid)
        {
            numsTmp[idx] = nums[p1];
            indexTmp[idx] = index[p1];
            idx++; p1++;
        }
        while(p2 <= ed)
        {
            numsTmp[idx] = nums[p2];
            indexTmp[idx] = index[p2];
            idx++;p2++;
        }
        for(int i = bgn; i <= ed; i++)
        {
            nums[i] = numsTmp[i];
            index[i] = indexTmp[i];
        }
    }
};

4. 翻转对

link:493. 翻转对 - 力扣（LeetCode）

思路：

        和前两道题思路相同，不过要先计算翻转对再合并排序

code

class Solution {
public:
    int ans = 0;
    std::vector<int>tmp;
    int reversePairs(vector<int>& nums) {
        // 不能和归并排序同步， 要先计算翻转对数再合并排序
        tmp.resize(nums.size());
        mergeSort(nums, 0, nums.size()-1);
        return ans;
    }

    void mergeSort(vector<int>& nums, int bgn, int ed)
    {
        if(bgn >= ed) return;
        // 分别排序
        int mid = (bgn + ed) >> 1;
        mergeSort(nums, bgn, mid);
        mergeSort(nums, mid + 1, ed);

        // 计算 ans

        // 策略二， 降序
        // 固定右边，从左边找第一个比固定数小的元素
        int p1 = bgn, p2 = mid + 1;
        while(p1 <= mid && p2 <= ed)
        {
            while(p2 <= ed && nums[p1] <= 2ll * nums[p2])// 判断
            {
                p2++;//出窗口
            }
            // [p2, ed]都符合要求
            ans += ed - p2 + 1;//更新
            p1++;//入窗口
        }

        // 合并排序
        p1 = bgn; 
        p2 = mid + 1; 
        int idx = bgn;
        while(p1 <= mid && p2 <= ed) tmp[idx++] = nums[p1] > nums[p2] ? nums[p1++] : nums[p2++];
        while(p1 <= mid) tmp[idx++] = nums[p1++];
        while(p2 <= ed) tmp[idx++] = nums[p2++];
        for(int i = bgn; i <= ed; i++)
        {
            nums[i] = tmp[i];
        }
    }
};

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
java计算机毕业设计（附源码）医疗资源分享平台（ssm+mysql+maven+LW文档）
C语言文件操作详解
Docker 安装 MySQL
【ChangeCLIP】Remote sensing change detection with multimodal vision-language representation learning
Lua--1.基础知识
【MySQL for Mac】终极解决——MySQL在Mac的字符集设置
JS入门难点解析11-构造函数，原型对象，实例对象
vue问题八：动态加载loading、浏览器图标
宝塔面板构架Node项目（PM2）以及PM2映射点击无反应的坑
04373 C++程序设计 2019版 第一章习题五、程序设计题
;