今天开始一个新的专题:数据结构当然,不仅仅适用于学习也适用于408考研。
那么提起数据结构
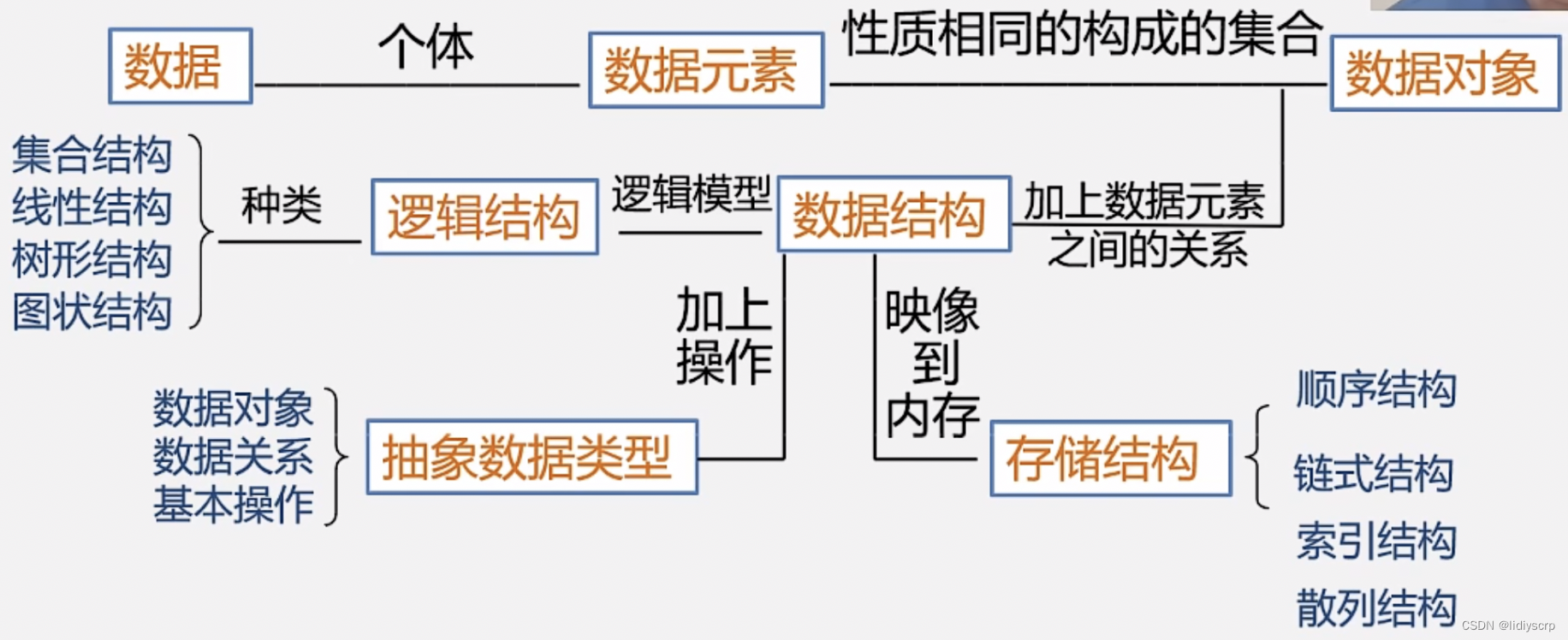
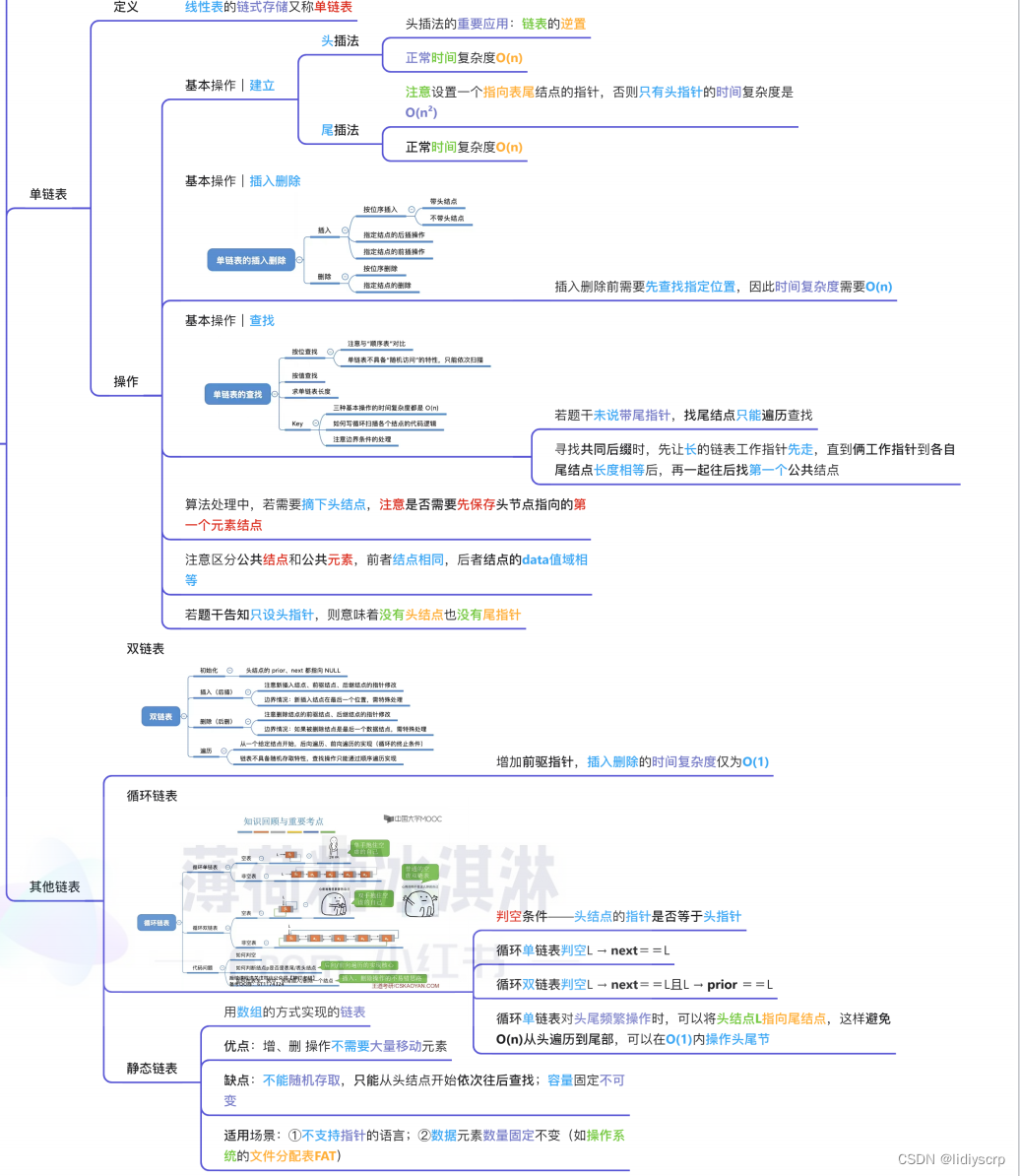
思维导图:总结如下:·
1.初识顺序表与链表
首先呢我们要明白,数据结构有物理结构,也有逻辑结构
物理结构
就是电脑实际的结构,链式,非链式,索引,散列
eg:
链式结构(Linked Structure)
例子:火车车厢
想象一列火车,每节车厢都连接在一起。每一节车厢(数据节点)都有一个链接(指针),连接到下一节车厢。这就是链式结构。要找到某一节车厢,你需要从第一节车厢开始,依次通过连接找到目标车厢。
非链式结构(Non-Linked Structure)
例子:书架
现在想象一个书架,上面整齐地排列着书籍。每本书(数据项)都直接放在一个固定的位置。你可以通过书的位置直接找到它,而不需要从第一本书开始逐本寻找。这就是非链式结构。
索引(Index)
例子:图书馆的目录卡片
想象一个图书馆,每本书在书架上的位置都通过一张目录卡片来记录。你可以先查找目录卡片(索引),找到书的位置,然后直接去拿书。这种方法提高了查找效率,因为你不需要在书架上一本本地找。
散列(Hashing)
**例子:钥匙和钥匙扣】
想象你有一个钥匙扣,上面挂着多把钥匙。每把钥匙上都有一个标签(哈希值),标明它对应的锁(数据位置)。当你要找某一把钥匙时,你通过钥匙上的标签很快就能找到它。这就是散列的基本原理,通过一个哈希函数(标签生成方式),可以快速找到数据的位置。
逻辑结构
简单讲就是脑子里面想的,分为线性与非线性
线性结构(Linear Structure) 例子:排队买票
想象你在电影院排队买票。大家一个接一个排成一条直线,这就是线性结构。每个人的位置是有序的,前面有一个人,后面也有一个人(除了队首和队尾)。
实际数据结构:数组和链表
- 数组:就像排队,每个人(元素)都有固定的位置(索引)。你可以通过位置(索引)快速找到任何一个人(元素)。
- 链表:也是线性结构,但每个人(节点)手里都有一个纸条,写着下一个人的名字(指针)。你要找到某个人,需要从第一个人开始,一个个问过去。
-
栈(Stack)
例子:书堆
想象一堆书,你只能从顶部添加或移除书。这就是栈的概念。栈是一种“后进先出”(Last In, First Out, LIFO)的结构。最新放进去的元素最先被取出来。
实际数据结构:栈
- 操作:
- 压栈(Push):在栈顶添加一个元素。
- 出栈(Pop):从栈顶移除一个元素。
- 栈顶(Top/Peek):查看栈顶的元素而不移除它。
-
队列(Queue)
例子:排队买票
想象在电影院排队买票,最早来的人最先买到票,最晚来的人最后买到票。这就是队列的概念。队列是一种“先进先出”(First In, First Out, FIFO)的结构。最先进入队列的元素最先被取出。
实际数据结构:队列
- 操作:
- 入队(Enqueue):在队尾添加一个元素。
- 出队(Dequeue):从队首移除一个元素。
- 队首(Front):查看队首的元素而不移除它。
非线性结构(Non-Linear Structure) 例子:家谱图
想象一个家谱图,它展示了一个家族的成员关系。祖先在上,后代在下,分支可能有很多。这就是非线性结构。每个人(节点)可以有多个孩子(指向多个节点)。
实际数据结构:树和图
- 树:就像家谱图,每个节点可以有多个子节点(孩子),但只有一个父节点(除了根节点)。例如,二叉树是一种特殊的树,每个节点最多有两个子节点。
- 图:比家谱图更复杂,每个节点可以和多个节点有连接(边)。例如,城市地图就是一个图结构,城市是节点,道路是边。
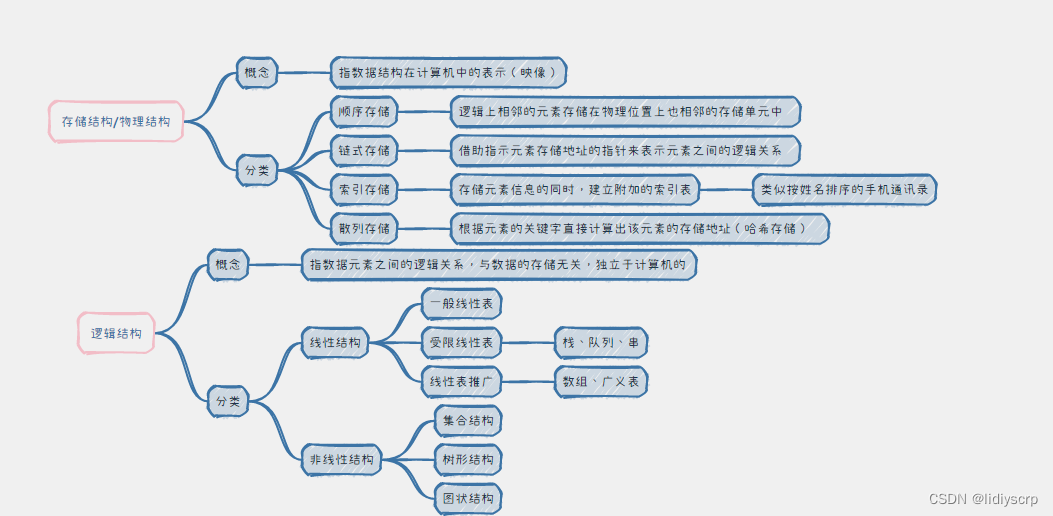
总结如下: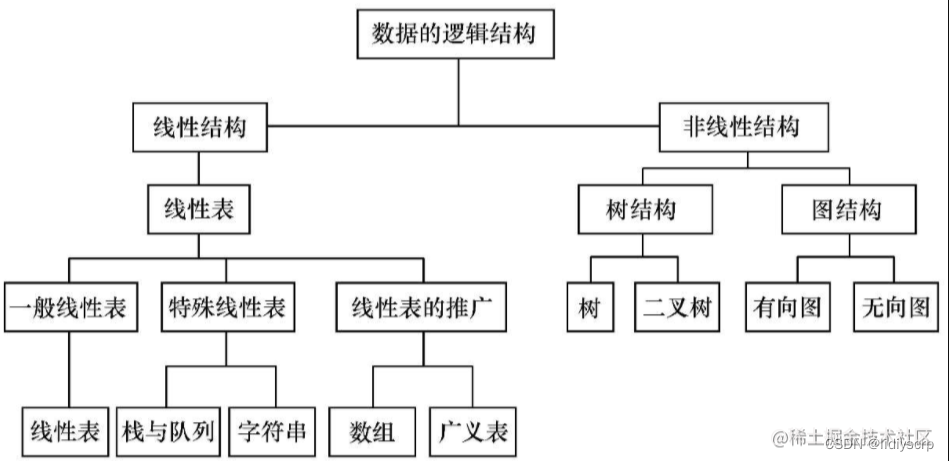
408常考题目:判断是逻辑还是物理结构.
技巧:指数据元素之间的逻辑关系,与数据的存储无关,独立于计算机的用于判断逻辑。
注意:哈希表是物理结构,与存储结构有关,循环队列也是。
关于站和队列,则是逻辑结构。
2.顺序表
开始线性表的学习了。
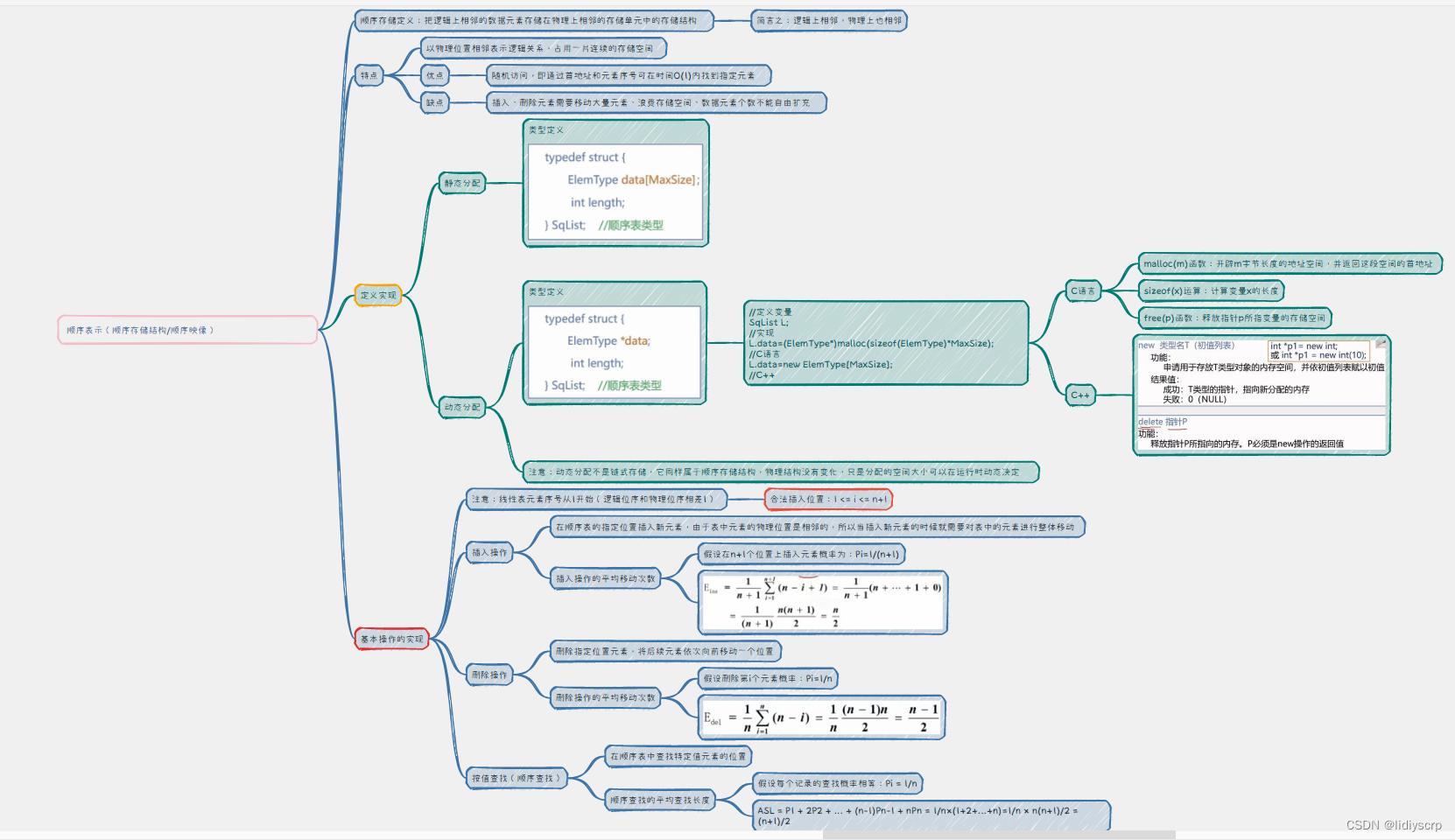
导图:
什么是顺序表呢?
类似于数组;
-
静态分配
-
类型定义
typedef struct { ElemType data[MaxSize]; int length; } SqList; -
typedef struct {...} SqList;
- 这段代码定义了一个结构体,并通过
typedef给它起了一个别名SqList。这样你可以使用SqList来声明这种结构体类型的变量,而不需要每次都写struct {...}。
- 这段代码定义了一个结构体,并通过
-
ElemType data[MaxSize];
data是一个数组,它的类型是ElemType,数组的大小是MaxSize。ElemType是一个占位符,通常在实际代码中会被替换为具体的数据类型,例如int、float或者自定义的数据类型。MaxSize是一个宏定义或常量,表示顺序表可以容纳的最大元素数量。
-
int length;
length用来记录顺序表当前的长度,即顺序表中实际包含的元素个数。
-
-
动态分配(好好讲讲)
struct SqList {
ElemType* data; // 指向动态分配数组的指针
int length; // 当前顺序表的长度
int maxSize; // 顺序表的最大容量
};
注意:这个可和链表不一样 注意:动态分配不是链式存储,它同样属于顺序存储结构,物理结构没有变化,只是分配的空间大小可以在运行时动态决定
具体用法:
1.初始化顺序表
// 构造函数,初始化顺序表
SqList(int maxSize) : maxSize(maxSize), length(0)
{
data = new ElemType[maxSize];
}
2.增加
// 增加元素到顺序表尾部
void insertElem(ElemType elem)
{ if (length >= maxSize)
{
throw std::overflow_error("顺序表已满,无法插入元素。");
}
data[length] = elem;
length++; }
// 在指定位置插入元素
void insertElemAt(int pos, ElemType elem) {
if (pos < 0 || pos > length) { // 注意:这里 pos 可以等于 length,表示在末尾插入
throw std::out_of_range("位置非法,无法插入元素。");
}
if (length >= maxSize) {
throw std::overflow_error("顺序表已满,无法插入元素。");
}
for (int i = length; i > pos; i--) {
data[i] = data[i - 1];
}
data[pos] = elem;
length++;
}
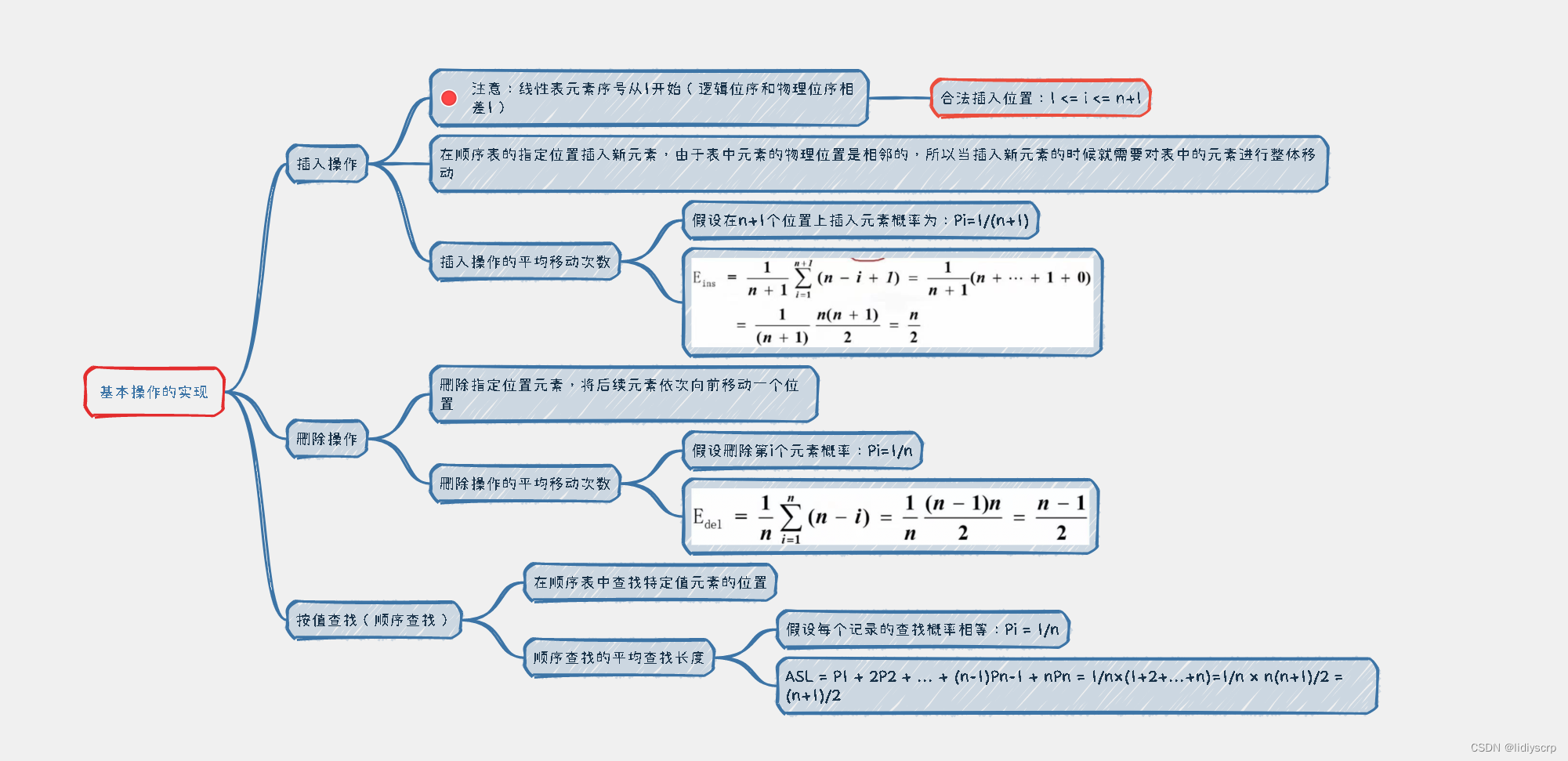
408里面 长度为n
注意:线性表元素序号从1开始(逻辑位序和物理位序相差1)
合法插入位置:1 <= i <= n+1(表尾)
代码改为: void insertElemAt(int pos, ElemType elem) {
if (pos < 1 || pos > length + 1) { // 合法位置范围为 1 <= pos <= length + 1
throw std::out_of_range("位置非法,无法插入元素。");
}
if (length >= maxSize) {
throw std::overflow_error("顺序表已满,无法插入元素。");
}
for (int i = length; i >= pos; i--) {
data[i] = data[i - 1];
}
data[pos - 1] = elem; // 将位置 pos 转换为索引 pos-1
length++;
}
3.删除
// 删除顺序表中指定位置的元素
void deleteElem(int pos) {
if (pos < 0 || pos >= length) {
throw std::out_of_range("位置非法,无法删除元素。");
}
for (int i = pos; i < length - 1; i++) {
data[i] = data[i + 1];
}
length--;
}
408里面 长度为n
注意:合法删除位置:1 <= i <= n
为了符合删除操作的合法位置约束(1 <= i <= n),需要对删除元素的位置进行适当的调整。C++ 中数组的索引从 0 开始,但在实际使用中,位置可能从 1 开始,因此需要进行相应的转换。在 C++ 实现中,我们需要对位置参数进行减1操作,以使其适应 C++ 中的数组索引。
void deleteElem(int pos) {
if (pos < 1 || pos > length) { // 合法位置范围为 1 <= pos <= length
throw std::out_of_range("位置非法,无法删除元素。");
}
for (int i = pos - 1; i < length - 1; i++) {
data[i] = data[i + 1];
}
length--;
}
4.修改
// 修改顺序表中指定位置的元素
void updateElem(int pos, ElemType newElem) {
if (pos < 0 || pos >= length) {
throw std::out_of_range("位置非法,无法修改元素。");
}
data[pos] = newElem;
}
5.查找
// 查询顺序表中指定位置的元素
ElemType getElem(int pos) const {
if (pos < 0 || pos >= length) {
throw std::out_of_range("位置非法,无法查询元素。");
}
return data[pos];
}
#include <iostream>
#include <stdexcept>
typedef int ElemType; // 定义顺序表中元素的类型
class SqList {
private:
ElemType* data; // 指向动态分配数组的指针
int length; // 当前顺序表的长度
int maxSize; // 顺序表的最大容量
public:
// 构造函数,初始化顺序表
SqList(int maxSize) : maxSize(maxSize), length(0) {
data = new ElemType[maxSize];
}
// 析构函数,销毁顺序表,释放内存
~SqList() {
delete[] data;
}
// 增加元素到顺序表尾部
void insertElem(ElemType elem) {
if (length >= maxSize) {
throw std::overflow_error("顺序表已满,无法插入元素。");
}
data[length] = elem;
length++;
}
// 删除顺序表中指定位置的元素
void deleteElem(int pos) {
if (pos < 0 || pos >= length) {
throw std::out_of_range("位置非法,无法删除元素。");
}
for (int i = pos; i < length - 1; i++) {
data[i] = data[i + 1];
}
length--;
}
// 修改顺序表中指定位置的元素
void updateElem(int pos, ElemType newElem) {
if (pos < 0 || pos >= length) {
throw std::out_of_range("位置非法,无法修改元素。");
}
data[pos] = newElem;
}
// 查询顺序表中指定位置的元素
ElemType getElem(int pos) const {
if (pos < 0 || pos >= length) {
throw std::out_of_range("位置非法,无法查询元素。");
}
return data[pos];
}
// 打印顺序表中的所有元素
void printList() const {
for (int i = 0; i < length; i++) {
std::cout << data[i] << " ";
}
std::cout << std::endl;
}
};
int main() {
try {
SqList list(10); // 初始化顺序表,最大容量为10
list.insertElem(5);
list.insertElem(10);
list.insertElem(15);
std::cout << "顺序表中的元素:";
list.printList();
ElemType elem = list.getElem(1);
std::cout << "位置1的元素是:" << elem << std::endl;
list.updateElem(1, 20);
std::cout << "修改后顺序表中的元素:";
list.printList();
list.deleteElem(0);
std::cout << "删除后顺序表中的元素:";
list.printList();
} catch (const std::exception& e) {
std::cerr << e.what() << std::endl;
}
return 0;
}
欧克!!!
3.链表:
第一个重点加难点开始了!!!
导图:
首先什么是链表?
为什么要有链表呢?
什么是链表:链表是一种数据结构,它由一系列节点(Node)组成,这些节点通过指针连接在一起。每个节点包含两个部分:数据部分和指针部分。数据部分存储具体的值,指针部分指向下一个节点。
为什么要有链表呢?
为了展示链表相对于顺序表(数组)的优点,我们可以通过几个具体的例子和故事来说明。在这些例子中,链表展示出其在动态调整和高效插入、删除操作方面的优势。
故事1:动态大小调整
场景:你是一名软件工程师,需要设计一个动态大小的联系人列表应用。
顺序表(数组):
- 你开始时创建一个包含100个空位的联系人数组。
- 随着用户不断添加联系人,数组很快被填满。
- 为了添加更多联系人,你必须创建一个更大的数组(例如200个空位),然后将现有联系人复制到新数组中,最后删除旧数组。
- 这个过程不仅复杂,还浪费时间和内存,因为你需要频繁地分配和复制大量数据。
链表:
- 你使用链表来实现联系人列表,每次添加联系人时,只需创建一个新节点,并将其链接到链表末尾。
- 由于链表可以动态调整大小,因此你不需要担心预先分配足够的空间,也不需要进行大规模的数据复制。
- 这种方法既简单又高效,特别适合用户数量不断增长的应用。
故事2:高效的插入和删除操作
场景:你是一名游戏开发者,需要实现一个实时更新的排行榜系统,玩家的分数会不断变化。
顺序表(数组):
- 玩家分数存储在一个数组中,每次有新分数时,你需要将其插入正确的位置以保持排序。
- 为了插入新分数,你必须移动数组中大量的元素,以便腾出插入位置。
- 例如,如果数组中有1000个元素,你需要将其移动多次才能插入新的分数,这将导致性能问题,特别是在实时更新的场景中。
链表:
- 你使用链表来实现排行榜,每次有新分数时,只需找到合适的位置,将新节点插入链表。
- 插入操作只需修改几个指针,无需移动大量数据。
- 这种方法在处理频繁插入和删除操作时更加高效,能够保证游戏的流畅性和实时性。
故事3:队列的实现
场景:你是一个银行系统开发者,需要设计一个顾客排队系统,每个顾客到达后加入队列,处理完后离开队列。
顺序表(数组):
- 你使用数组来实现队列,顾客到达时加入数组尾部,离开时从数组头部移除。
- 每次移除顾客后,你需要将数组中剩余的元素向前移动,以保持队列的正确顺序。
- 这种方法效率低下,特别是当队列长度很大时,移动操作会耗费大量时间。
链表:
- 你使用链表来实现队列,顾客到达时创建一个新节点并将其链接到链表尾部,离开时移除链表头部的节点。
- 由于链表的节点是动态链接的,因此移除头节点只需修改指针,无需移动其他节点。
- 这种方法不仅高效,还能处理大量顾客的到达和离开操作,保证银行系统的流畅运行。
总结
通过这些例子可以看出,链表在以下几个方面具有显著优势:
- 动态大小调整:链表不需要预先分配固定大小,可以根据需要动态增长。
- 高效的插入和删除操作:链表插入和删除操作只需修改指针,无需移动大量数据。
- 适用于队列和栈的实现:链表能够高效地实现队列和栈等数据结构,特别适用于需要频繁操作的场景。
虽然链表在某些方面具有优势,但它也有自己的缺点,如随机访问效率低和额外的内存开销。因此,选择使用链表还是顺序表,应该根据具体应用场景的需求来决定。
单链表
链表结构
typedef struct LNode {
ElementType data; // 存储数据的类型,可以是任意类型
struct LNode *next; // 指向链表中下一个节点的指针
} LNode,*Linklist;
struct LNode:定义了一个结构体类型,名为LNode,它包含两个成员:data和next。data是数据域,用于存储节点的数据;next是指针域,用于指向链表中的下一个节点。
LNode:在typedef声明中,LNode是struct LNode的别名。这意味着你可以使用LNode来声明这种结构体类型的变量,定义链表L:LinkList L; 定义结点指针p:LNode *P;
注:通常用头指针来标识一个单链表,如单链表L,头指针为NULL时表示一个空表。此外,为了操作上的方便,在单链表第一个结点之前附加一个结点,称为头结点。头结点的数据域可以不设任何信息,也可以记录表长等信息。头结点的指针域指向线性表的第一个元素结点头结点和头指针的区分:不管带不带头结点,头指针都始终指向链表的第一个结点,而头结点是带头结点的链表中的第一个结点,结点内通常不存储信息。
引入头结点后,可以带来两个优点:
①由于第一个数据结点的位置被存放在头结点的指针域中,因此在链表的第一个位置上的操作和在表的其他位置上的操作一致,无须进行特殊处理。
②无论链表是否为空,其头指针都指向头结点的非空指针(空表中头结点的指针域为空),因此空表和非空表的处理也就得到了统一。
为了方便操作接下来的操作我们统一使用带头结点的链表。
如何创建单链表呢?
1.初始化链表:
创建一个头节点,其next指针初始化为NULL。
Linklist L; // 定义链表L
L = new LNode; // 动态分配头节点
L->next = NULL; // 头节点的next指针指向NULL或者
LNode *L = new LNode; // 动态分配头节点
L->next = NULL; // 头节点的next指针指向NULL
2.定义节点指针:
声明一个指向LNode的指针p,用于创建和插入新节点。
LNode *p; // 定义结点指针p
3. 头插法建立单链表
头插法是一种在链表中插入节点的方法,新节点总是插入到链表的头部。这意味着新节点会成为链表的第一个节点,而原来的头节点则会成为新节点的下一个节点。
下面用图形展示头插法插入节点的过程:
初始链表:
假设我们有一个链表,链表中的节点依次为
A -> B -> C -> D。
Head->[A] -> [B] -> [C] -> [D]创建新节点:
创建一个新的节点
X。将新节点插入到头部:
将新节点
X的next指针指向原来的头节点A,然后更新链表的头指针指向新节点X。
新节点X 的 next -> A
Head-> [X] -> [A] -> [B] -> [C] -> [D]用图形表示,步骤如下:
初始链表:
Head | [A] -> [B] -> [C] -> [D]创建新节点
[X]插入新节点:
Head | [X] -> [A] -> [B] -> [C] -> [D]
头插法插入节点:
使用头插法,每次插入新节点时,都需要将新节点的next指针指向当前头节点的next,然后将头节点的next指向新节点。
void InsertHead(Linklist &L, ElementType value) {
LNode *newNode = new LNode; // 创建新节点
newNode->data = value; // 设置新节点的数据
newNode->next = L->next; // 新节点指向原头节点的下一个节点
L->next = newNode; // 头节点指向新节点
}
构建链表:
使用循环或其他逻辑来接收数据,并使用InsertHead函数将数据插入链表。
// 假设ElementType是int类型
int data;
cout << "Enter data (-1 to end): ";
while (cin >> data && data != -1) {
InsertHead(L, data); // 插入数据到链表头部
}4.尾插法建立单链表
初始化链表:
链表只有一个头节点 Head,它指向 NULL,表示链表是空的。
Head -> NULL
插入第一个节点:
创建一个新节点 A,将头节点的 next 指向 A,并将 A 的 next 指向 NULL。
Head -> [A] -> NULL
插入第二个节点:
创建一个新节点 B,找到链表的尾部节点(目前是 A),将 A 的 next 指向 B,并将 B 的 next 指向 NULL。
Head -> [A] -> [B] -> NULL
插入第三个节点:
创建一个新节点 C,找到链表的尾部节点(目前是 B),将 B 的 next 指向 C,并将 C 的 next 指向 NULL。
Head -> [A] -> [B] -> [C] -> NULL
插入第四个节点:
创建一个新节点 D,找到链表的尾部节点(目前是 C),将 C 的 next 指向 D,并将 D 的 next 指向 NULL。
Head -> [A] -> [B] -> [C] -> [D] -> NULL
单指针
#include <iostream>
using namespace std;
// 定义链表节点结构
struct LNode {
int data; // 节点的数据域
LNode *next; // 节点的指针域
};
// 尾插法插入节点
void InsertTail(LNode *&L, int value) {
LNode *newNode = new LNode; // 创建新节点
newNode->data = value; // 设置新节点的数据
newNode->next = NULL; // 新节点的next指针指向NULL
LNode *p = L; // 从头节点开始
while (p->next != NULL) { // 找到链表的尾部节点
p = p->next;
}
p->next = newNode; // 将尾节点的next指针指向新节点
}
int main() {
// 初始化链表
LNode *L = new LNode; // 动态分配头节点
L->next = NULL; // 头节点的next指针指向NULL
int data;
cout << "Enter data (-1 to end): ";
while (cin >> data && data != -1) {
InsertTail(L, data); // 插入数据到链表尾部
}
// 打印链表
LNode *current = L->next; // 跳过头节点,从第一个数据节点开始
while (current != NULL) {
cout << current->data << " ";
current = current->next;
}
cout << endl;
// 释放链表节点内存
current = L;
while (current != NULL) {
LNode *temp = current;
current = current->next;
delete temp;
}
return 0;
}
带尾指针
#include <iostream>
using namespace std;
// 定义链表节点结构
struct LNode {
int data; // 节点的数据域
LNode *next; // 节点的指针域
};
// 尾插法插入节点
void InsertTail(LNode *&L, LNode *&tail, int value) {
LNode *newNode = new LNode; // 创建新节点
newNode->data = value; // 设置新节点的数据
newNode->next = NULL; // 新节点的next指针指向NULL
tail->next = newNode; // 尾节点的next指针指向新节点
tail = newNode; // 更新尾节点为新节点
}
int main() {
// 初始化链表
LNode *L = new LNode; // 动态分配头节点
L->next = NULL; // 头节点的next指针指向NULL
LNode *tail = L; // 定义尾指针,并初始指向头节点
int data;
cout << "Enter data (-1 to end): ";
while (cin >> data && data != -1) {
InsertTail(L, tail, data); // 插入数据到链表尾部
}
// 打印链表
LNode *current = L->next; // 跳过头节点,从第一个数据节点开始
while (current != NULL) {
cout << current->data << " ";
current = current->next;
}
cout << endl;
// 释放链表节点内存
current = L;
while (current != NULL) {
LNode *temp = current;
current = current->next;
delete temp;
}
return 0;
}
5.删除节点(按位置)
- 删除节点:
- 检查位置是否有效。
- 遍历链表到要删除节点的前一个节点。
- 修改前一个节点的
next指针,以跳过要删除的节点。- 释放要删除节点的内存。
#include <iostream>
using namespace std;
// 定义链表节点结构
struct LNode {
int data; // 节点的数据域
LNode *next; // 节点的指针域
};
// 尾插法插入节点
void InsertTail(LNode *&L, LNode *&tail, int value) {
LNode *newNode = new LNode; // 创建新节点
newNode->data = value; // 设置新节点的数据
newNode->next = NULL; // 新节点的next指针指向NULL
tail->next = newNode; // 尾节点的next指针指向新节点
tail = newNode; // 更新尾节点为新节点
}
// 删除指定位置的节点(假设位置从1开始,头节点位置为0,不删除头节点)
void DeleteNode(LNode *&L, int position) {
if (position <= 0) {
cout << "Invalid position!" << endl;
return;
}
LNode *p = L; // 指向头节点
int count = 0;
while (p->next != NULL && count < position - 1) {
p = p->next;
count++;
}
if (p->next == NULL || count != position - 1) {
cout << "Position out of range!" << endl;
return;
}
LNode *temp = p->next; // 要删除的节点
p->next = temp->next; // 前一个节点指向要删除节点的下一个节点
delete temp; // 释放要删除节点的内存
}
int main() {
// 初始化链表
LNode *L = new LNode; // 动态分配头节点
L->next = NULL; // 头节点的next指针指向NULL
LNode *tail = L; // 定义尾指针,并初始指向头节点
// 插入一些节点
InsertTail(L, tail, 1);
InsertTail(L, tail, 2);
InsertTail(L, tail, 3);
InsertTail(L, tail, 4);
// 打印链表
LNode *current = L->next; // 跳过头节点,从第一个数据节点开始
cout << "Original List: ";
while (current != NULL) {
cout << current->data << " ";
current = current->next;
}
cout << endl;
// 删除指定位置的节点
int position;
cout << "Enter position to delete (1-based index): ";
cin >> position;
DeleteNode(L, position);
// 打印链表
current = L->next; // 跳过头节点,从第一个数据节点开始
cout << "Updated List: ";
while (current != NULL) {
cout << current->data << " ";
current = current->next;
}
cout << endl;
// 释放链表节点内存
current = L;
while (current != NULL) {
LNode *temp = current;
current = current->next;
delete temp;
}
return 0;
}
删除节点函数详细解释
void DeleteNode(LNode *&L, int position)
void 表示这个函数没有返回值。
DeleteNode 是函数名。
LNode *&L 是一个引用类型的指针参数,表示链表的头节点。使用引用可以直接修改链表。
int position 表示要删除节点的位置,从1开始计数。
检查位置有效性
if (position <= 0) { cout << "Invalid position!" << endl; return; }
这部分代码用于检查传入的位置是否有效。如果位置小于等于0,则认为是无效位置,打印错误信息并返回。
初始化指针
LNode *p = L; // 指向头节点 int count = 0;
LNode *p = L; 初始化一个指针 p,指向链表的头节点。
int count = 0; 初始化一个计数器 count,用于记录当前遍历到的位置。
遍历链表
while (p->next != NULL && count < position - 1) { p = p->next; count++; }
while (p->next != NULL && count < position - 1) 是一个循环,用于遍历链表,直到找到要删除节点的前一个节点。
p->next != NULL 确保 p 不是最后一个节点。
count < position - 1 确保遍历到要删除节点的前一个位置。
在循环中:
p = p->next; 将 p 指向下一个节点。
count++; 计数器增加1。
检查位置是否超出范围
if (p->next == NULL || count != position - 1) { cout << "Position out of range!" << endl; return; }
这部分代码用于检查是否找到要删除的位置:
p->next == NULL 表示链表中没有那么多节点,位置超出链表长度。
count != position - 1 表示计数器没有达到要删除节点的前一个位置。
如果满足上述条件之一,打印错误信息并返回。
删除节点
LNode *temp = p->next; // 要删除的节点 p->next = temp->next; // 前一个节点指向要删除节点的下一个节点 delete temp; // 释放要删除节点的内存
LNode *temp = p->next; 保存要删除的节点的指针 temp。
p->next = temp->next; 将前一个节点的 next 指针指向要删除节点的下一个节点,实现跳过要删除的节点。
delete temp; 释放要删除节点的内存,避免内存泄漏。
6.按值查找与按位查找
LNode* SearchByValue(LNode *L, int value) {
LNode *p = L->next; // 从头节点的下一个节点开始查找
while (p != NULL && p->data != value) {
p = p->next;
}
return p; // 返回找到的节点或NULL
}
LNode* SearchByValue(LNode *L, int value)定义按值查找函数。
LNode *L是链表的头节点。int value是要查找的值。LNode *p = L->next;初始化指针p,从头节点的下一个节点开始查找(跳过头节点)。while (p != NULL && p->data != value)遍历链表:
p != NULL确保没有到达链表末尾。p->data != value确保当前节点的数据域不等于要查找的值。p = p->next;移动指针到下一个节点。return p;返回找到的节点,或者NULL(如果未找到)。
LNode* SearchByPosition(LNode *L, int position) {
if (position <= 0) {
return NULL; // 无效位置返回NULL
}
LNode *p = L->next; // 从头节点的下一个节点开始查找
int count = 1;
while (p != NULL && count < position) {
p = p->next;
count++;
}
return p; // 返回找到的节点或NULL
}
LNode* SearchByPosition(LNode *L, int position)定义按位查找函数。
LNode *L是链表的头节点。int position是要查找的节点位置,从1开始。if (position <= 0)检查位置是否有效:
return NULL;如果位置无效,返回NULL。LNode *p = L->next;初始化指针p,从头节点的下一个节点开始查找(跳过头节点)。int count = 1;初始化计数器count。while (p != NULL && count < position)遍历链表:
p != NULL确保没有到达链表末尾。count < position确保计数器没有达到指定位置。p = p->next;移动指针到下一个节点。count++;计数器增加1。return p;返回找到的节点,或者NULL(如果未找到)。
7.改节点data值
1.先按位查找,再改即可。不过多了解。
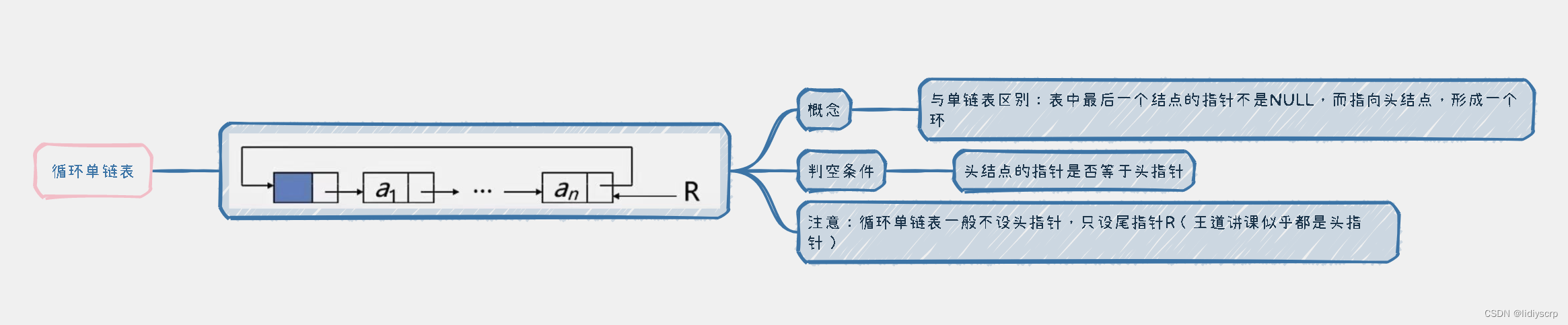
循环单链表
1.链表结构与单链表相同。
循环单链表和单链表的区别在于,表中最后一个结点的指针不是NULL,而改为指向头结点从而整个链表形成一个环。
在循环单链表中,表尾结点*r的next域指向T,故中没有指针域为NULL的结点,因此循环单链表的判空条件不是头结点的指针是否为空,而是它是否等于头指针。
循环单链表的插入、删除算法与单链表的几乎一样,所不同的是若操作是在表尾进行,则执行的操作不同,以让单链表继续保持循环的性质。当然,正是因为循环单链表是一个“环”,因此在任何一个位置上的插入和删除操作都是等价的,无须判断是否是表尾。
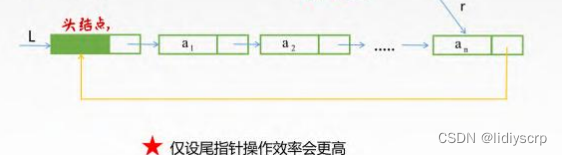
在单链表中只能从表头结点开始往后顺序遍历整个链表,而循环单链表可以从表中的任意一个结点开始遍历整个链表。有时对单链表常做的操作是在表头和表尾进行的,此时对循环单链表不设头指针而仅设尾指针,从而使得操作效率更高。其原因是,若设的是头指针,对表尾进行操作害要 0m)的时间复余度,而者设的是库指针r,r->next 即为头指针,对表头与表尾进行操作都只需要O(1)的时间复杂度,判空(head=head-Next)
简单代码
#include <iostream>
typedef int ElementType; // 假设ElementType为int类型,可根据需要更改
// 定义链表节点结构体
typedef struct LNode {
ElementType data; // 数据域
struct LNode *next; // 指针域,指向下一个节点
} LNode, *LinkList;
// 初始化循环单链表,带头结点
void InitList(LinkList &L) {
L = new LNode; // 创建头结点
L->next = L; // 头结点的next指向自己,构成循环
}
// 按位查找,返回第i个元素的地址
LNode* GetElem(LinkList L, int i) {
if (i < 0) return nullptr; // 无效位置返回nullptr
LNode *p = L; // p指向头结点
int j = 0; // 初始化计数器
while (p && j < i) { // 查找第i个节点
p = p->next;
j++;
}
return p;
}
// 按值查找,返回值为e的第一个节点的地址
LNode* LocateElem(LinkList L, ElementType e) {
LNode *p = L->next; // p指向第一个节点
while (p != L && p->data != e) { // 遍历链表
p = p->next;
}
if (p == L) return nullptr; // 没找到返回nullptr
return p;
}
// 插入操作,在第i个位置插入元素e
bool ListInsert(LinkList &L, int i, ElementType e) {
LNode *p = GetElem(L, i-1); // 找到第i-1个节点
if (!p) return false; // 第i-1个节点不存在,插入失败
LNode *s = new LNode; // 创建新节点
s->data = e; // 设置数据域
s->next = p->next; // 插入节点
p->next = s;
return true;
}
// 删除操作,删除第i个元素
bool ListDelete(LinkList &L, int i, ElementType &e) {
LNode *p = GetElem(L, i-1); // 找到第i-1个节点
if (!p || !p->next) return false; // 第i-1或第i个节点不存在,删除失败
LNode *q = p->next; // p的下一个节点q即为要删除的节点
p->next = q->next; // 将p的next指向q的next
e = q->data; // 保存删除节点的数据
delete q; // 释放q节点的内存
return true;
}
// 遍历链表
void TraverseList(LinkList L) {
LNode *p = L->next; // p指向第一个节点
while (p != L) { // 遍历链表
std::cout << p->data << " ";
p = p->next;
}
std::cout << std::endl;
}
int main() {
LinkList L;
InitList(L); // 初始化链表
// 插入数据
ListInsert(L, 1, 10);
ListInsert(L, 2, 20);
ListInsert(L, 3, 30);
std::cout << "链表内容: ";
TraverseList(L);
// 按位查找
LNode *p = GetElem(L, 2);
if (p) std::cout << "第2个元素: " << p->data << std::endl;
// 按值查找
p = LocateElem(L, 20);
if (p) std::cout << "找到值为20的元素: " << p->data << std::endl;
// 删除元素
ElementType e;
if (ListDelete(L, 2, e)) std::cout << "删除第2个元素: " << e << std::endl;
std::cout << "链表内容: ";
TraverseList(L);
return 0;
}
注释一下
1.初始化链表:
void InitList(LinkList &L) { L = new LNode; L->next = L; }创建头结点并让其
next指向自己,形成循环。L->next = L;正好可以判空。2.按位查找:
LNode* GetElem(LinkList L, int i) { if (i < 0) return nullptr; LNode *p = L; int j = 0; while (p && j < i) { p = p->next; j++; } return p; }3.按值查找:
LNode* LocateElem(LinkList L, ElementType e) { LNode *p = L->next; while (p != L && p->data != e) { p = p->next; } if (p == L) return nullptr; return p; }4.在第
i个位置插入元素e,实际是在第i-1个节点之后插入。bool ListInsert(LinkList &L, int i, ElementType e) { LNode *p = GetElem(L, i-1); if (!p) return false; LNode *s = new LNode; s->data = e; s->next = p->next; p->next = s; return true; }
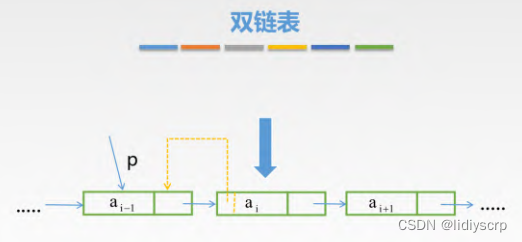
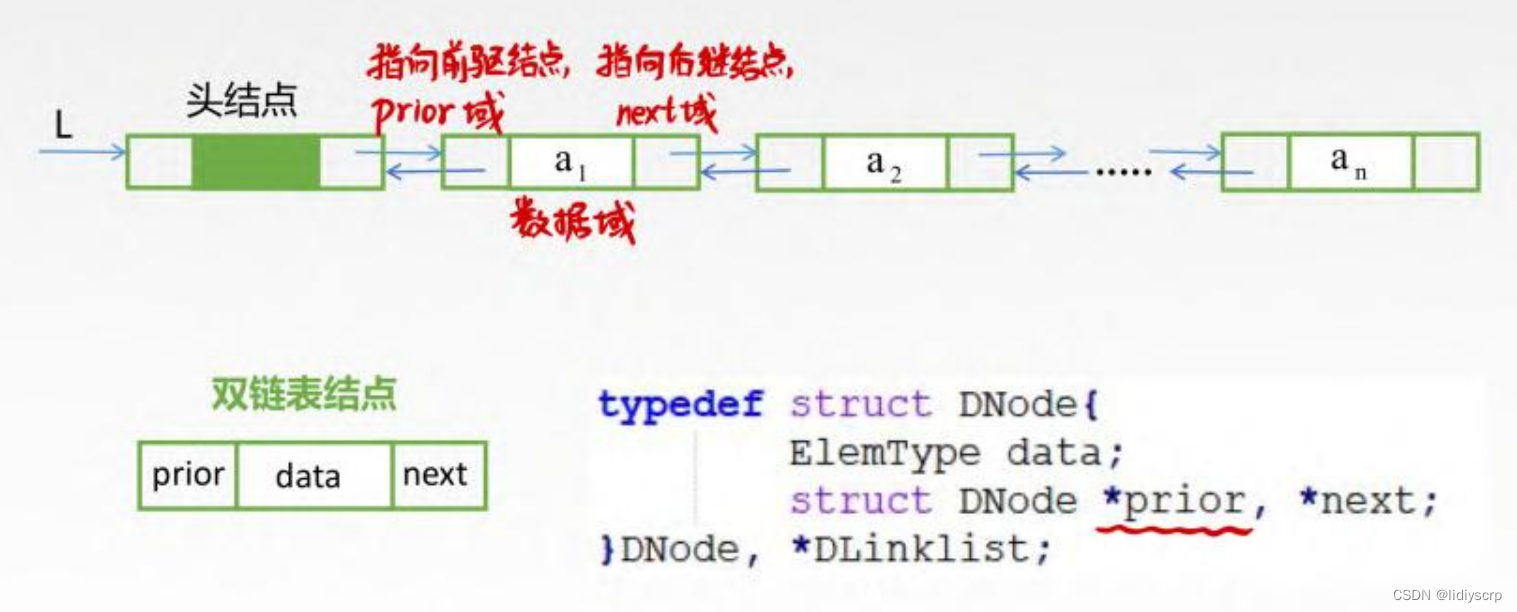
双链表
链表结构
typedef struct DNodei //定义双链表结点类型
{ElemType data; //数据域
struct DNode *prior,*next; //前驱和后继指针
}DNode,*DLinklist;
1.初始化链表:
DLinklist L; // 定义双链表L
L = new DNode; // 动态分配头节点
L->prior = L->next = NULL; // 头节点的prior和next指针指向NULL2.建立双链表
可以通过循环或特定逻辑来接收数据,并逐个插入节点。
DNode *newNode, *tail = L; // tail用于记录链表的最后一个节点
for (int i = 0; i < n; ++i) {
cin >> elem; // elem是待插入的元素
newNode = new DNode;
newNode->data = elem;
newNode->prior = tail;
if (tail != L) // 如果tail不是头节点
tail->next = newNode;
else // 否则,链表为空,需要设置头节点的next
L->next = newNode;
tail = newNode; // 更新tail为新节点
}
定义节点和链表: 首先,我们定义了一个双链表节点的结构体
DNode,它包含数据域data和指向前一个节点prior以及后一个节点next的指针。DLinklist是指向DNode的指针的别名,用于操作双链表。初始化指针:
newNode是用于存放新创建节点的指针,tail是用于记录链表最后一个节点的指针。初始时,tail指向头节点L。循环插入节点: 使用
for循环来接收用户输入的数据,每次循环都会创建一个新的节点并插入到双链表中。读取数据:
cin >> elem;这行代码是从标准输入读取一个数据,存储在变量elem中。创建新节点:
newNode = new DNode;这行代码使用new操作符创建了一个新的DNode节点。设置节点数据:
newNode->data = elem;将用户输入的数据赋值给新节点的数据域。设置前驱指针:
newNode->prior = tail;将新节点的前驱指针指向当前的最后一个节点。更新链表: 如果
tail不是头节点(即链表至少有一个节点),则将tail->next指向新节点。如果tail是头节点,说明链表为空,这时需要设置头节点的next指向新节点。更新最后一个节点:
tail = newNode;将tail更新为新节点,因为新节点现在是链表的最后一个节点。结束循环: 循环继续,直到所有数据都被读取并插入链表。xx
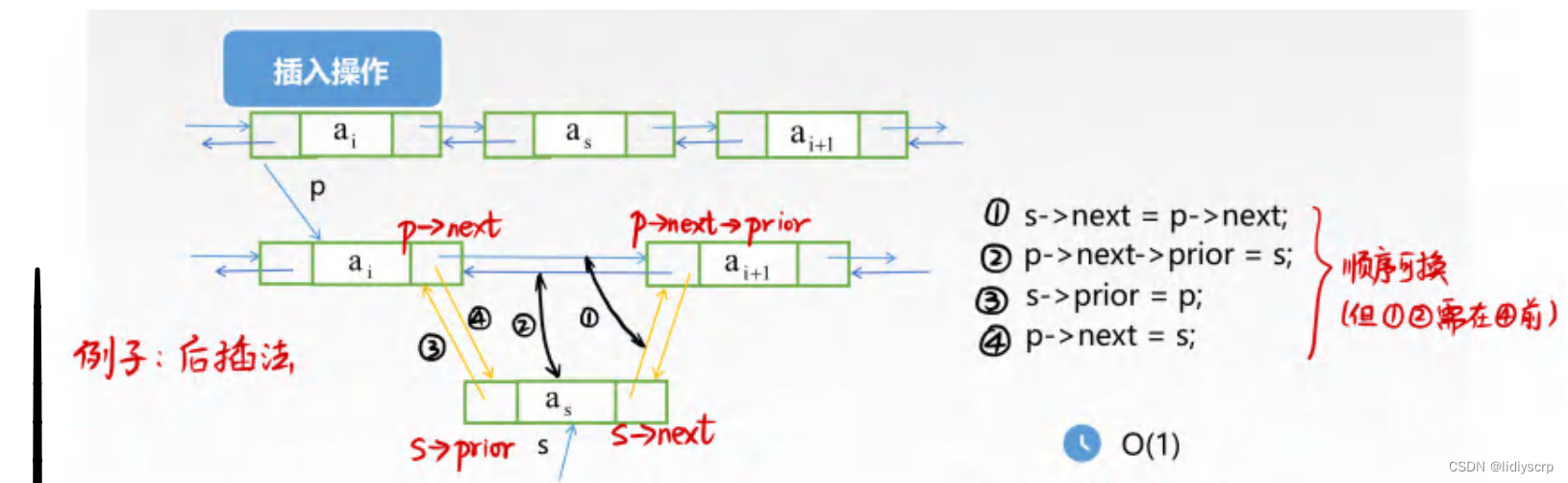
3.插入节点
void InsertDLinklist(DLinklist &L, DNode *p, ElemType value) {
DNode *newNode = new DNode;
newNode->data = value;
if (p == L) { // 如果p是头节点
newNode->next = L->next;
newNode->prior = L;
L->next = newNode;
if (newNode->next != NULL)
newNode->next->prior = newNode;
} else {
newNode->next = p;
newNode->prior = p->prior;
p->prior->next = newNode;
p->prior = newNode;
}
}注意:408同学一定要相信断链小心,以及表尾操作
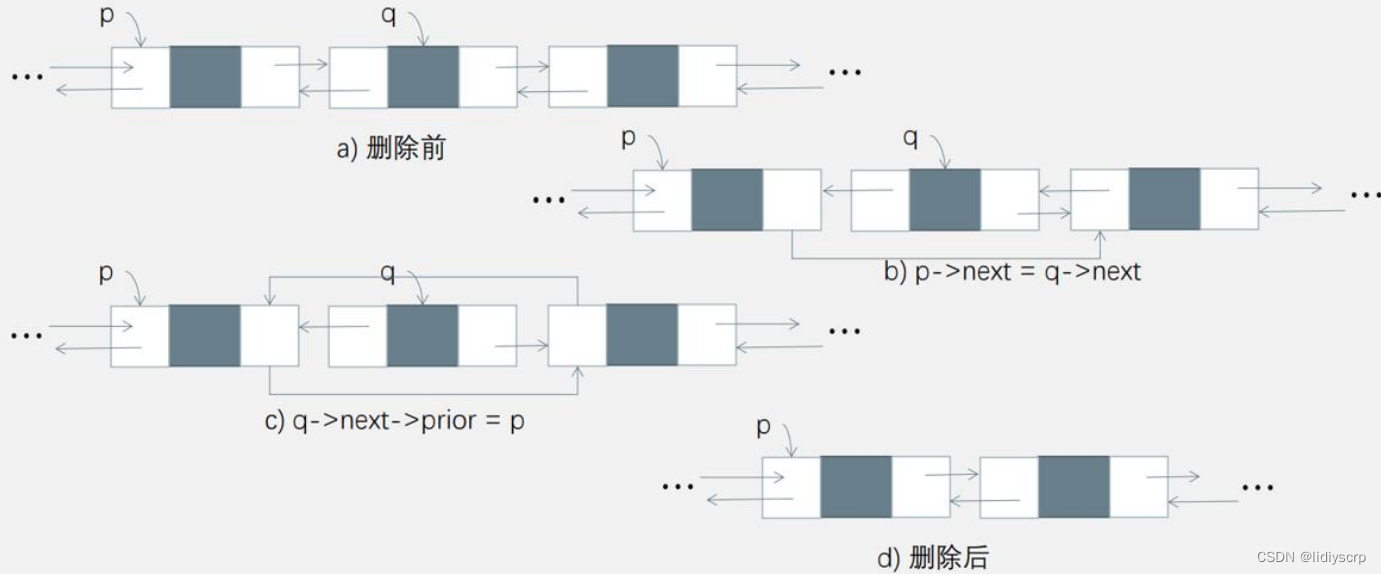
4.删除节点
void DeleteDLinklist(DLinklist L, DNode *p) {
if (p == L) { // 如果p是头节点
L->next = p->next;
if (L->next != NULL)
L->next->prior = L;
} else {
p->prior->next = p->next;
if (p->next != NULL)
p->next->prior = p->prior;
}
delete p;
}
详细解释这段代码是如何工作的。这段代码是一个函数,其目的是从双链表中删除一个指定的节点。这里是一步步的解释:
函数定义:
void DeleteDLinklist(DLinklist L, DNode *p)定义了一个函数,接受两个参数:双链表的头节点指针L和要删除的节点指针p。检查是否是头节点:
if (p == L)这个条件判断要删除的节点p是否是头节点。在双链表中,头节点是一个空节点,它的data域不存储数据,主要用于方便地访问链表的开始位置。删除头节点: 如果
p是头节点,那么执行以下操作:
L->next = p->next;将头节点的next指针指向要删除节点的next节点,这样就跳过了要删除的头节点。if (L->next != NULL) L->next->prior = L;如果新的头节点的next不是NULL,那么更新这个节点的prior指针,使其指向头节点。删除非头节点: 如果
p不是头节点,那么执行以下操作:
p->prior->next = p->next;将p的前驱节点的next指针指向p的后继节点,这样就从链表中移除了p。if (p->next != NULL) p->next->prior = p->prior;如果p有后继节点(不是尾结点),那么更新这个后继节点的prior指针,使其指向p的前驱节点。删除节点:
delete p;这行代码释放了p节点所占用的内存。这是必要的步骤,以避免内存泄漏。函数结束: 函数没有返回值,因为被删除的节点已经被从链表中移除,并且其内存已经被释放。
5.按值查找与按位查找
按值查找:
按值查找节点,需要遍历链表直到找到匹配的节点。DNode *FindDLinklist(DLinklist L, ElemType key) {
DNode *p = L->next; // 从头节点的下一个节点开始遍历
while (p != NULL && p->data != key)
p = p->next;
return p;
}
按位查找:
按位查找通常指的是按索引查找节点,需要知道链表的长度。DNode *FindDLinklistByPosition(DLinklist L, int position) {
DNode *p = L->next; // 从头节点的下一个节点开始遍历
int count = 0;
while (p != NULL && count != position) {
p = p->next;
++count;
}
return p;
}
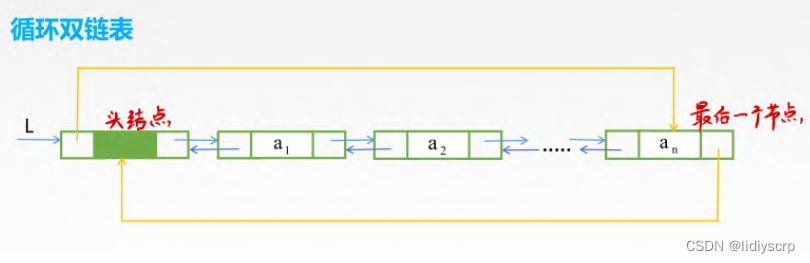
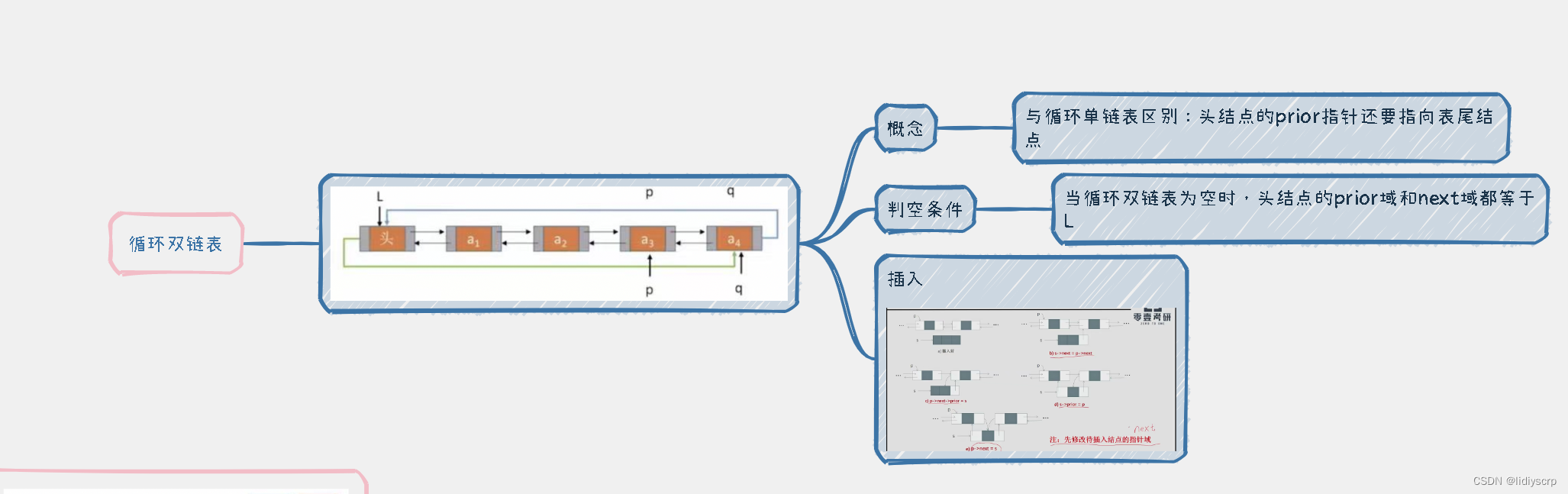
循环双链表
链表结构
typedef struct DNodei //定义双链表结点类型
{ElemType data; //数据域
struct DNode *prior,*next; //前驱和后继指针
}DNode,*DLinklist;
注:表中插入删除与双链表相同
1.插入
双向循环链表的插入(时间复杂度 O(n))核心思想: 不要“断链” ,不要先处理插入位置的前驱节点的后继指针。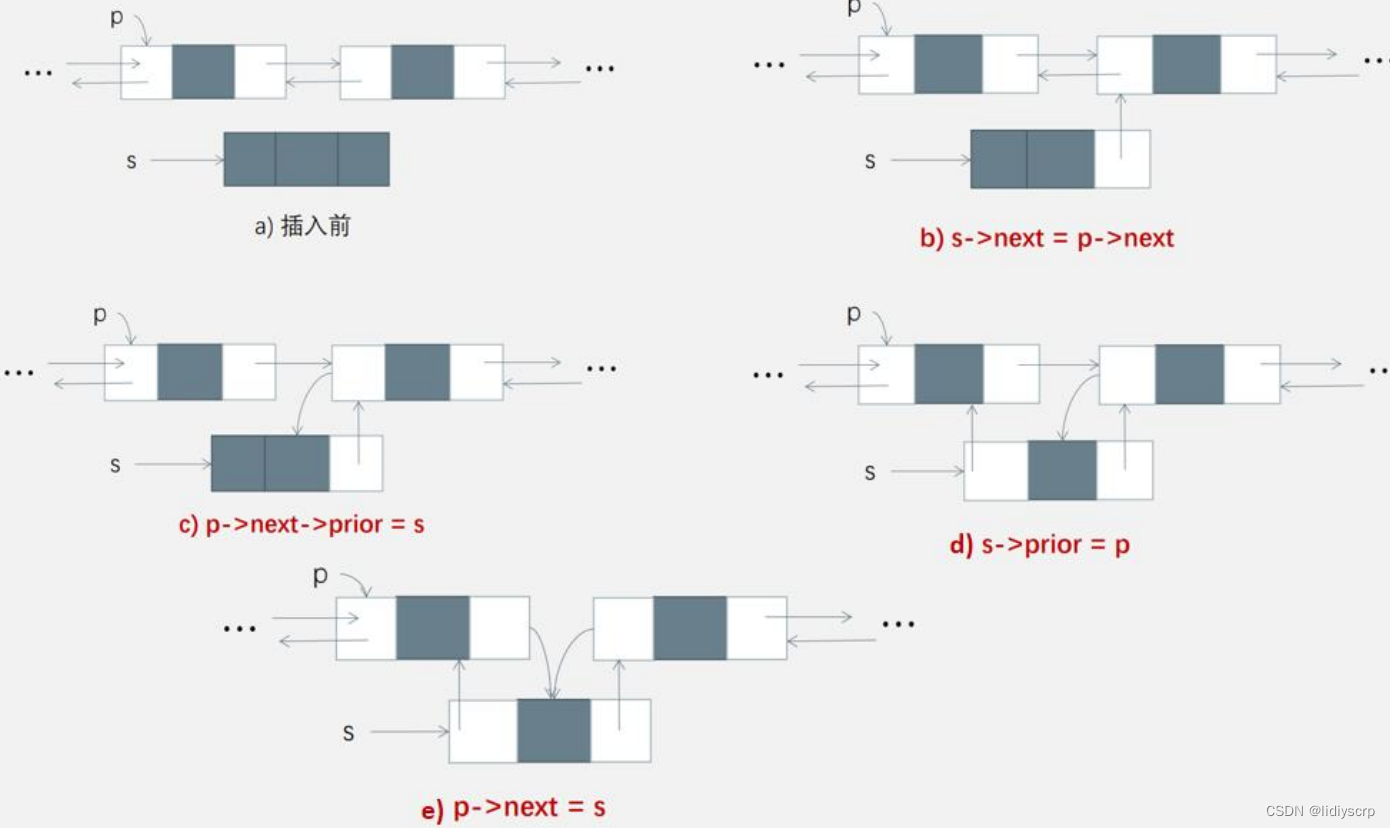
2.删除
3.在无头结点的循环双链表进行,表首/表尾的插入删除。
表首插入(在链表头部插入新元素):
创建新节点:使用malloc或new分配内存给新节点。
更新新节点指针:将新节点的prior指向链表的最后一个节点,next指向链表的第一个节点。
更新链表首尾节点的指针:将链表最后一个节点的next指向新节点,第一个节点的prior指向新节点。
void InsertHead(DulLinkList &L, ElemType value) { DulNode *newNode = (DulNode *)malloc(sizeof(DulNode)); newNode->data = value; newNode->prior = L->prior; newNode->next = L; L->prior->next = newNode; L = newNode; // 更新链表的头指针为新节点 }
表尾插入(在链表尾部插入新元素):
找到当前链表的最后一个节点:通过从头节点开始遍历链表直到next指针指向头节点的节点。
创建新节点:同表首插入。
更新新节点指针:将新节点的next指向头节点,prior指向找到的最后一个节点。
更新尾节点和头节点的指针:将尾节点的next指向新节点,头节点的prior指向新节点。
void InsertTail(DulLinkList L, ElemType value) { DulNode *newNode = (DulNode *)malloc(sizeof(DulNode)); newNode->data = value; newNode->next = L->next; // 新节点的next指向当前第一个节点 newNode->prior = L; // 新节点的prior指向尾节点 L->next->prior = newNode; // 将当前第一个节点的prior指向新节点 L->next = newNode; // 更新尾节点的next为新节点 }
表首删除(删除链表头部的元素):
找到链表的第一个节点:链表的头节点L的next指针指向第一个节点。
删除节点:将第一个节点的next所指向的节点的prior指向头节点,头节点的next指向要删除节点的next。
释放内存:释放要删除节点的内存。
void DeleteHead(DulLinkList L, ElemType *e) { if (L->next != L) { *e = L->next->data; // 保存被删除节点的数据 L->next = L->next->next; // 移动头指针 L->next->prior = L; // 更新新的第一个节点的prior free(L->prior); // 释放被删除节点的内存 } else { // 链表为空或只有一个节点的情况 } }
表尾删除(删除链表尾部的元素):
找到当前链表的最后一个节点:同表尾插入。
删除节点:将最后一个节点的prior所指向的节点的next指向头节点,头节点的prior指向要删除节点的prior。
释放内存:同表首删除。void DeleteTail(DulLinkList L, ElemType *e) { DulNode *tail = L->prior; // 找到尾节点 if (tail != L) { *e = tail->data; // 保存被删除节点的数据 tail->prior->next = L; // 更新前一个节点的next L->prior = tail->prior;// 更新头节点的prior free(tail); // 释放被删除节点的内存 } else { // 链表为空或只有一个节点的情况 } }
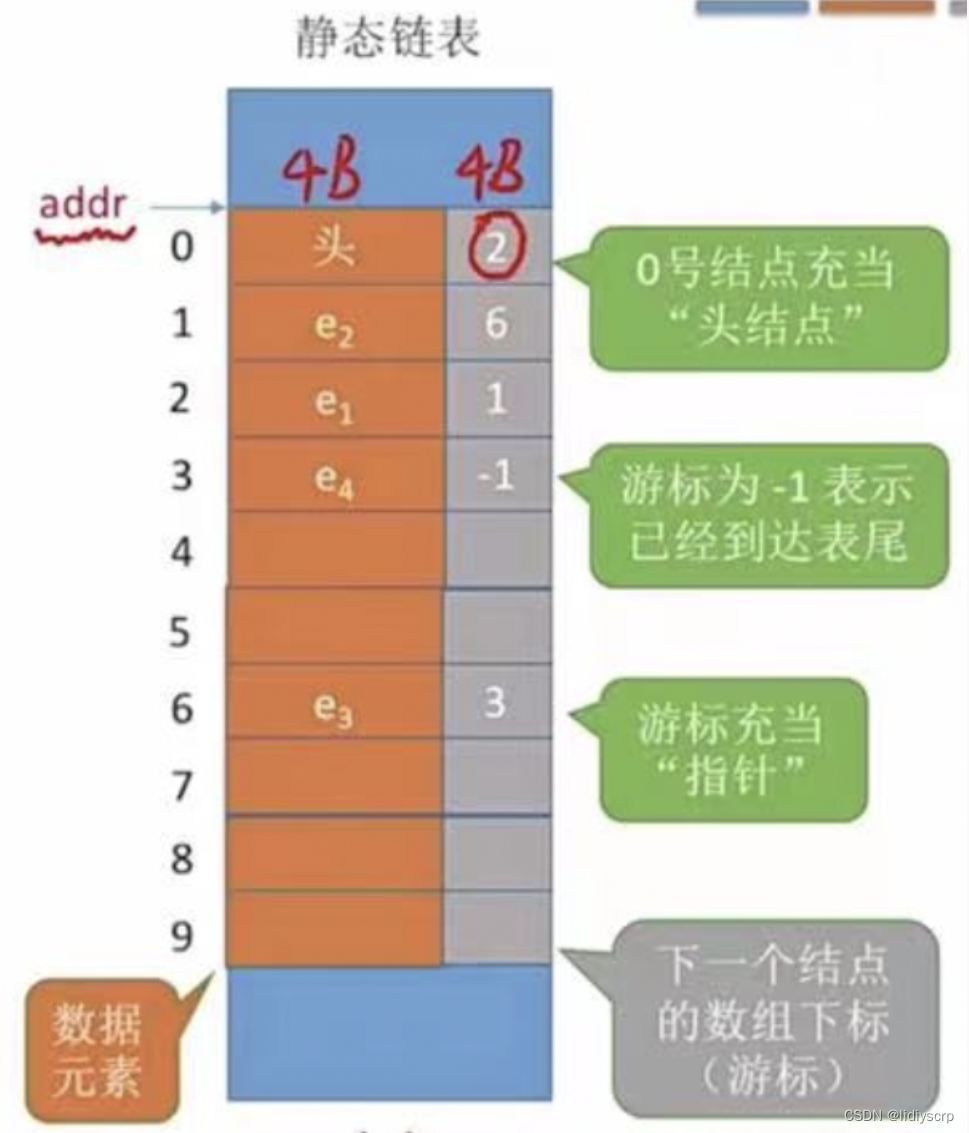
静态链表
-
概念
-
静态链表借助数组来描述线性表的链式存储结构,结点也有数据域和指针域,其指针是结点的相对地址(数组下标,又称游标)
-
-
特点
-
需要预先分配一块连续内存空间(容量固定不变)、插入删除无需移动元素、不能随机存取
-
-
适用场景
-
不支持指针的低级语言、数据元素数量固定不变的场景(如操作系统的文件分配表FAT)
-
在静态链表中有个约定俗称的规定:
1.第一个和最后一个结点作为特殊元素处理,不存数据。
2.我们通常把未被使用的数组元素称之为备用链表,而数组第一个元素(即下标为0的元素)的Cur就存放备用链表的第一个结点的下标。3. 数组最后一个元素的Cur则存放第一个有数值的元素(首元结点)的下标,相当于单链表中头结点的作用。当整个链表为空的时候,数组中最后一个元素的Cur为0。
4.如果一个结点下一位置的数据为空但这个结点数据不为空,则这个结点的Cur用0来表示。因为这个这是最后一个有数据的结点了,没有下一个有数据的结点了,所以Cur为0相当于指针中的NULL
原文链接:https://blog.csdn.net/shsbsns/article/details/13148397(静态链表更详细)
最后:
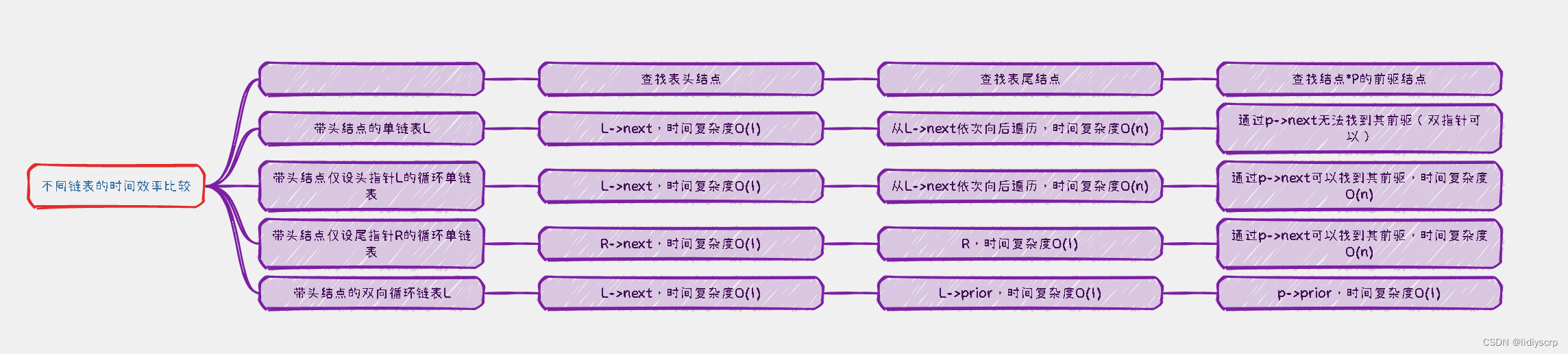
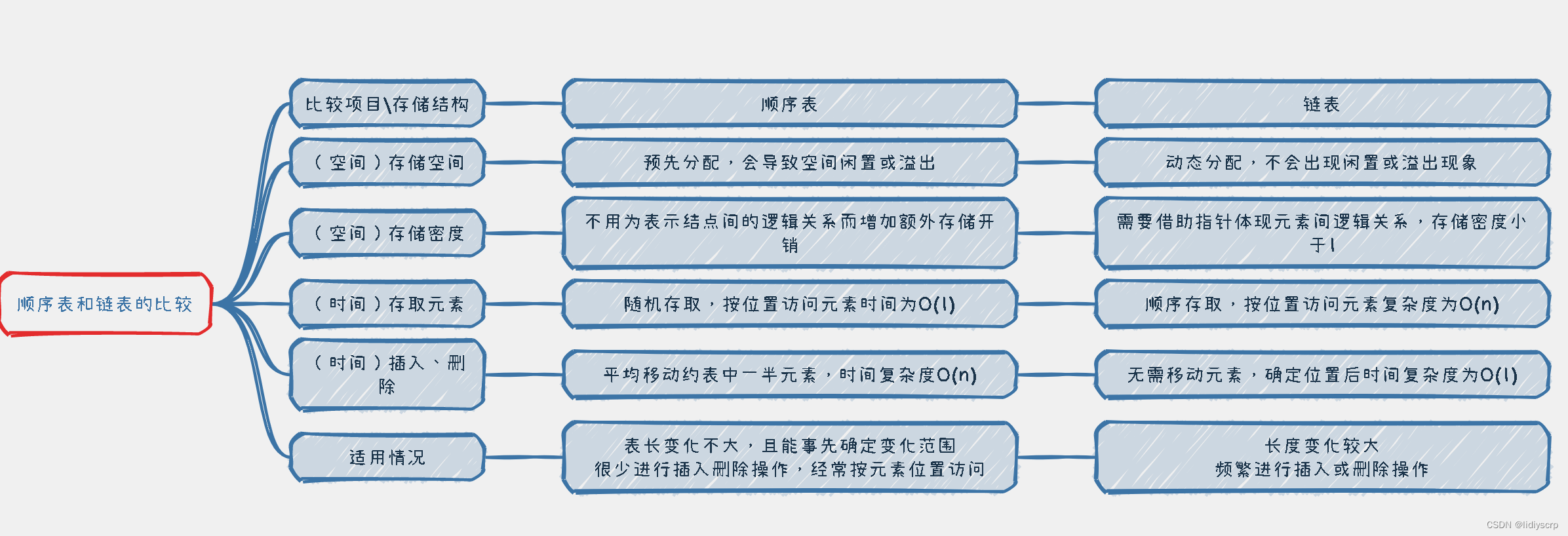
继续比较
如果喜欢该专栏麻烦点个赞,评论支持一下谢谢。
(以上引用部分图片,只做交流学习,无商业用途,违权必换)