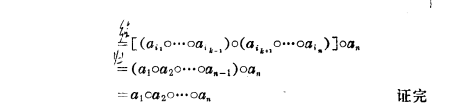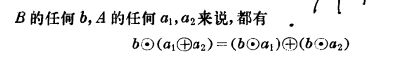基础知识

	集合和映射,集合见上一篇
	映射的定义可以看出 可以是多个元到一个元的映射,也就是说可以是向量到实数.
	其次是定义域是每个点(向量)都要有对应

映射的效果相同说明是映射相等,过程无关

代数运算 由关系到一个元素====一种特殊的映射


二元运算----------------运算的封闭性

结合律

交换律

分配律 =====两种运算之间的一种关系



满射和单射


一一映射的重要性质
记住很重要,但是更重要的是证明是一一映射的方法
有来有回,也就是有单射有满射


注意事项:

变换:

同态映射:两种运算之间的关系

满同态: 前提是映射,而后是满射

运算的交换律结合律分配律都是一致的 证明方法同下

同构: 这个不就是一种运算给换成另一种运算吗

极其重要的自同构:
前面有提到过,一个有限的集合只能和自己同映射,但是无限的集合可以和子集构成映射