Theory

3D Tensor and Axes

When dealing with a 3D tensor, such as the one we had in the previous example, it can be conceptualized as a collection of 2D matrices or blocks, stacked along a new dimension. The axes represent the following:

1. First Component (axis=0) - Batch Size / Number of Blocks:

   • Direction along the batch size or the stack of matrices.
   • When you have a 3D tensor, this first dimension essentially tells you how many blocks (matrices) you have.
   • This axis essentially indexes the individual blocks in your collection.
   • For example, if the shape is (2, 2, 3), the value 2 in the first position tells you there are 2 blocks.

2. Second Component (axis=1) - Rows of Each Block (Matrix):

   • Represents the rows within each matrix or block.
   • When referring to axis 1, you are looking along the rows within each individual block.
   • For each block (or matrix), you have multiple rows. In the example of shape (2, 2, 3), the second 2 refers to the fact that each block has 2 rows.

3. Third Component (axis=2) - Columns of Each Block (Matrix):

   • Represents the columns within each row of a matrix.
   • When referring to axis 2, you are looking at the columns within each row of a matrix.
   • In the example of shape (2, 2, 3), the 3 refers to the fact that each row has 3 columns.

Conceptual Visualization

Consider the example we used:

arr_3d = np.array([
[[ 1, 2, 3], # Block 0, Row 0 
[ 4, 5, 6]], # Block 0, Row 1 
[[ 7, 8, 9], # Block 1, Row 0
[10, 11, 12]]# Block 1, Row 1
])

The shape of this array is (2, 2, 3), which can be described as follows:

• 2 Blocks (first dimension) → We have 2 blocks or matrices.
• 2 Rows per block (second dimension) → Each block has 2 rows.
• 3 Columns per row (third dimension) → Each row has 3 columns.

Axis Summary:

• axis = 0: Refers to the batch size or block level.

  • Example: Summing along this axis means combining all the corresponding elements from each block.

• axis = 1: Refers to the rows within each block.

  • Example: Summing along this axis means summing across rows within each block.

• axis = 2: Refers to the columns within each row.

  • Example: Summing along this axis means summing across columns within each row.

Practical Meaning

• The first axis (axis=0) typically represents a batch when you're dealing with data processing. For instance, in machine learning models, this is commonly the batch size—how many examples are being processed in parallel.
• The second axis (axis=1) represents the rows of each block (matrix). In data like images, this could represent the height of the image (number of rows of pixels).
• The third axis (axis=2) represents the columns of each block (matrix). For images, this could represent the width of the image (number of columns of pixels).

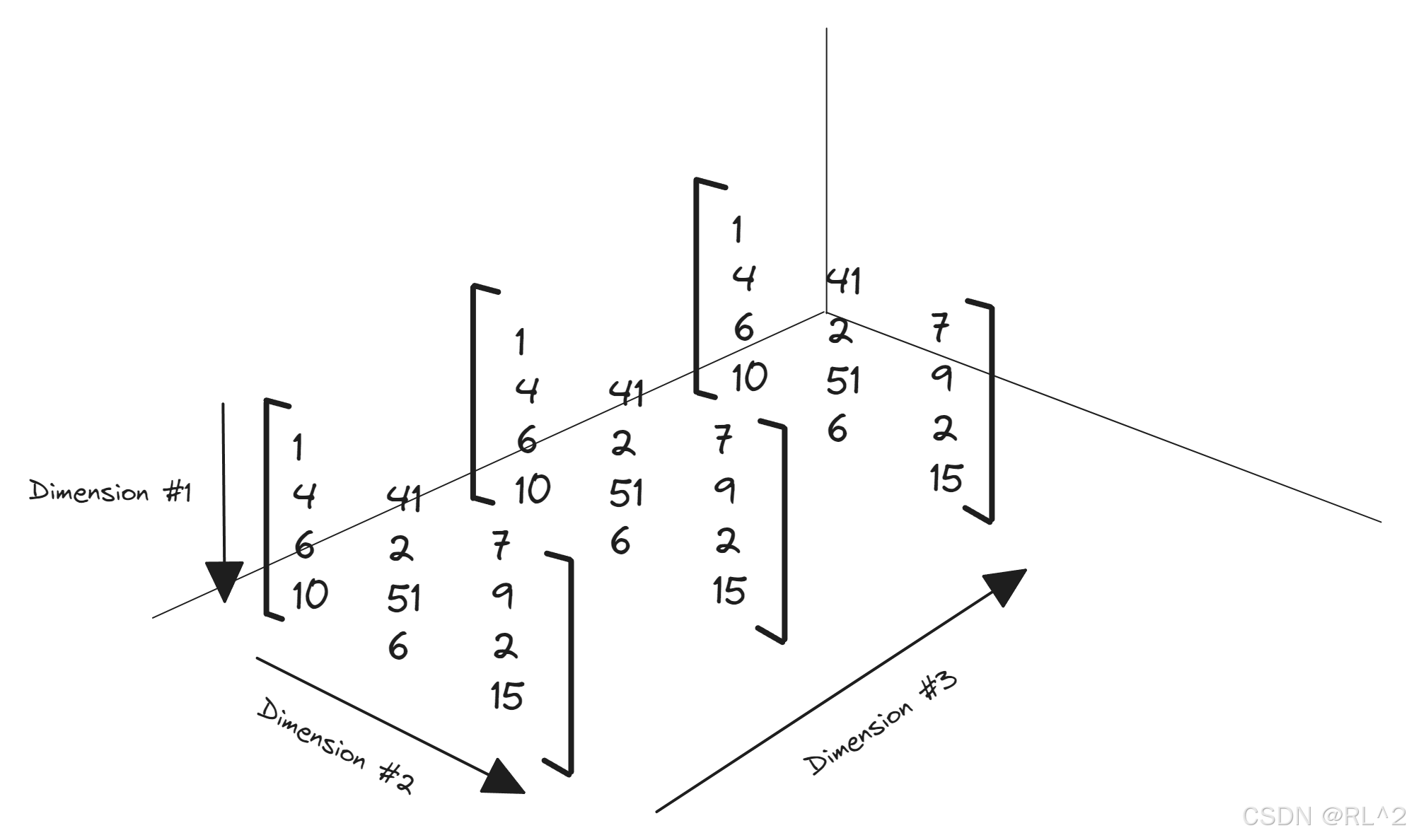
As is shown in the above picture, dimension#3 is the axis 0 of a tensor in python

dimension#1 is the axis 1 of a tensor in python

dimension#2 is the axis 2 of a tensor in python

Examples

Consider the following 3D array:

import numpy as np
 # Create a 3D array arr_3d = np.array([
[[ 1, 2, 3], 
[ 4, 5, 6]], 

[[ 7, 8, 9],
 [10, 11, 12]]
]) 

# The shape of arr_3d is (2, 2, 3) # It has 2 blocks, each with 2 rows and 3 columns.

This 3D array can be visualized as having two 2x3 matrices (blocks).

.sum(0) - Summing along the First Axis (Combining Blocks)

• axis=0 means we are summing along the first axis, which corresponds to stacking the blocks on top of each other and summing along that dimension.

result_0 = arr_3d.sum(0) 
print("Sum along axis 0:\n", result_0)
# Output: # [[ 8 10 12] # [14 16 18]]

Explanation:

• Summing along axis 0 means adding the corresponding elements from each of the two blocks:
  • [1 + 7, 2 + 8, 3 + 9] = [8, 10, 12] (first row of the result).
  • [4 + 10, 5 + 11, 6 + 12] = [14, 16, 18] (second row of the result).

.sum(1) - Summing along the Second Axis (Combining Rows within Each Block)

• axis=1 means we are summing along the second axis, which corresponds to summing across the rows within each block.

result_1 = arr_3d.sum(1) 
print("Sum along axis 1:\n", result_1) 
# Output: # [[ 5 7 9] # [17 19 21]]

Explanation:

• Summing along axis 1 means adding the rows together within each block:
  • For the first block ([[1, 2, 3], [4, 5, 6]]):
    • [1 + 4, 2 + 5, 3 + 6] = [5, 7, 9].
  • For the second block ([[7, 8, 9], [10, 11, 12]]):
    • [7 + 10, 8 + 11, 9 + 12] = [17, 19, 21].

.sum(2) - Summing along the Third Axis (Summing Across Columns)

• axis=2 means we are summing along the third axis, which corresponds to summing across the columns within each row.

result_2 = arr_3d.sum(2) 
print("Sum along axis 2:\n", result_2) 
# Output: # [[ 6 15] # [ 24 33]]

Explanation:

• Summing along axis 2 means summing across the columns within each row:
  • For the first block:
    • First row: 1 + 2 + 3 = 6
    • Second row: 4 + 5 + 6 = 15
  • For the second block:
    • First row: 7 + 8 + 9 = 24
    • Second row: 10 + 11 + 12 = 33

.sum(-1) - Summing along the Last Axis (Equivalent to .sum(2) in a 3D Array)

• axis=-1 always refers to the last axis. In this case, the last axis is axis 2, which corresponds to summing across the columns within each row. Therefore, .sum(-1) will give the same result as .sum(2).

result_minus_1 = arr_3d.sum(-1) 
print("Sum along axis -1:\n", result_minus_1) 
# Output: # [[ 6 15] # [ 24 33]]

Explanation:

• Since axis=-1 refers to the last axis, which is axis 2 in this case, it produces the same output as .sum(2):
  • For the first block:
    • First row: 1 + 2 + 3 = 6
    • Second row: 4 + 5 + 6 = 15
  • For the second block:
    • First row: 7 + 8 + 9 = 24
    • Second row: 10 + 11 + 12 = 33

Summary Table

These examples illustrate how different axes are used to reduce the tensor along specific dimensions. Summing along a particular axis effectively removes that dimension and produces a new array with fewer dimensions.