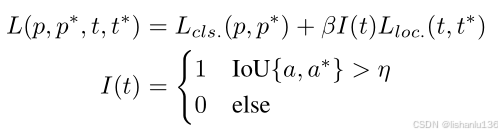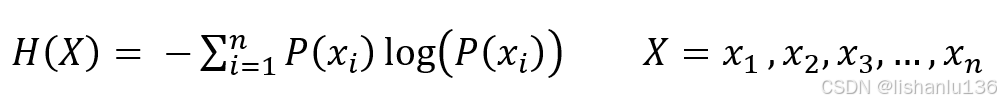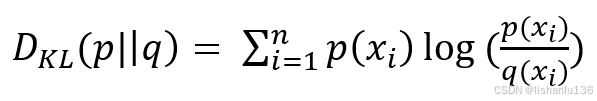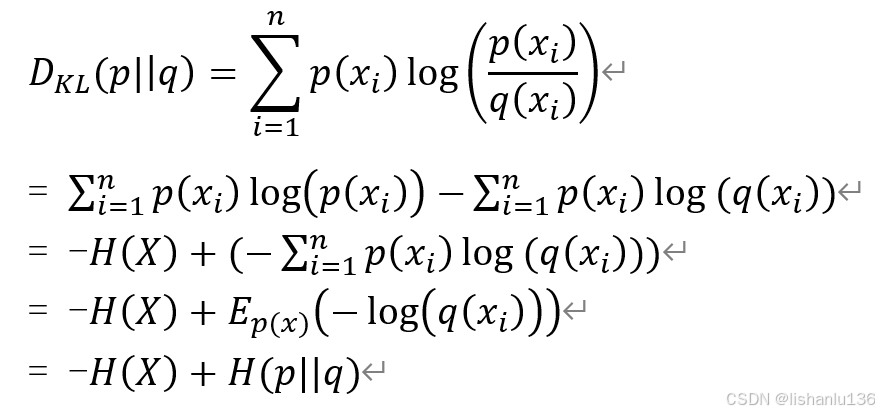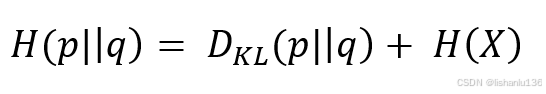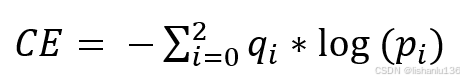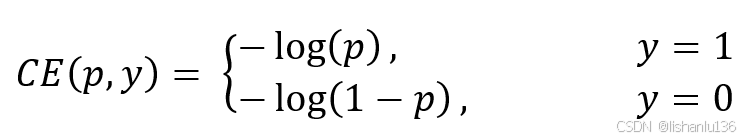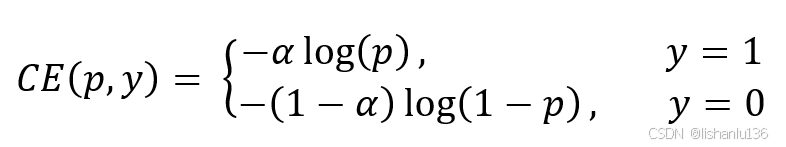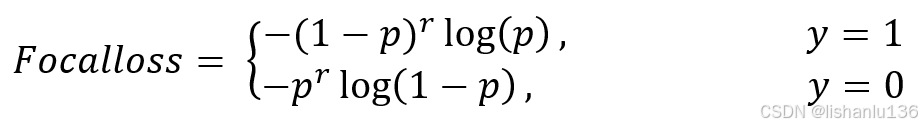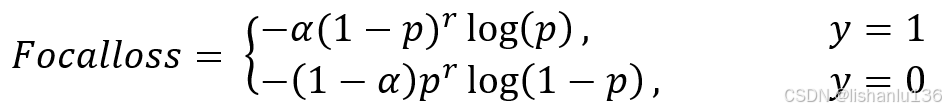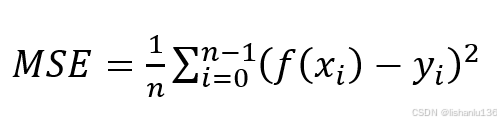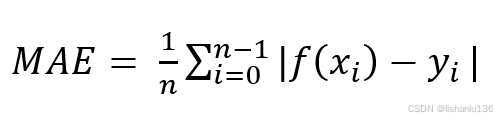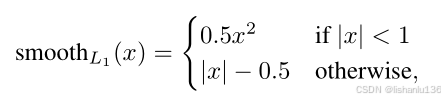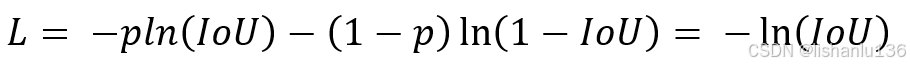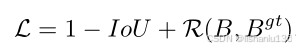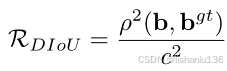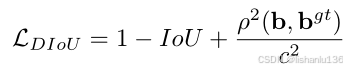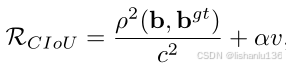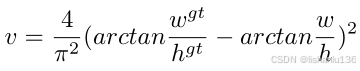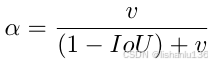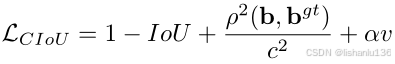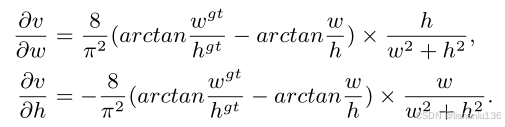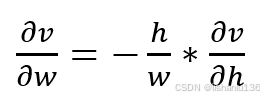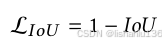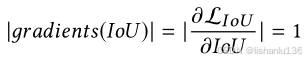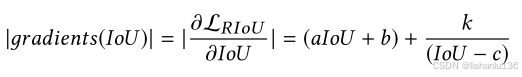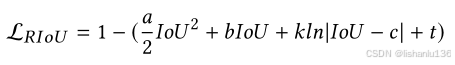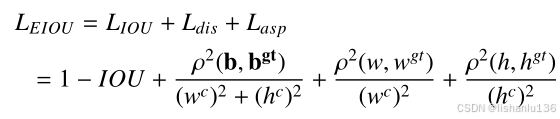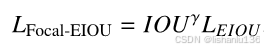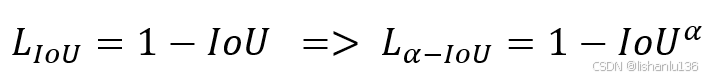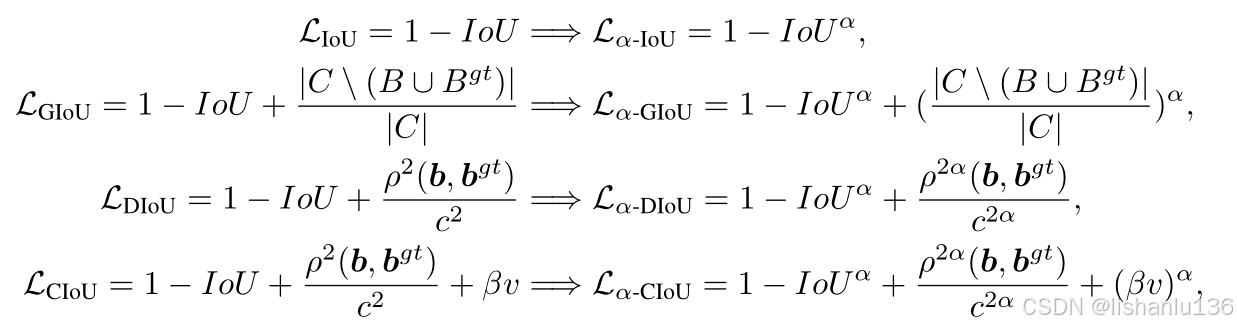损失函数是用来衡量模型与数据的匹配程度的,也是模型权重更新的基础。计算损失产生模型权重的梯度,随后通过反向传播算法,模型权重得以更新进而更好地适应数据。一般情况下,目标损失函数包含两部分损失,一个是目标框分类损失,一个是目标框定位损失,两者共同构成目标检测问题的损失形式。
文章目录
目标检测算法通用损失函数可写作:
它主要由目标框分类损失和目标框回归损失两部分组成,其中目标框回归损失部分只有IoU大于阈值η的样本才参与损失计算。
1、分类损失
分类损失是用来评价预测类别与实际类别的偏离程度的,早期像YOLOv1和YOLOv2就简单采用MSE/L2损失。后面大多采用交叉熵损失(Cross-Entropy Loss)。为提高分类效率,也为了提高模型泛化能力,解决噪声标签上的过信度(标注数据存在噪声,标签过度自信)问题,提出了标签平滑(Label Smooth);为了解决类别不平衡和分类难度差异问题,设计了焦点损失(Focal loss)。这些改进都是在CE Loss的基础上进行改进的。
1.1 交叉熵损失函数CE Loss
交叉熵损失函数(Cross-Entropy Loss)是机器学习和深度学习中常用的一种损失函数。它在神经网络中通常与 softmax 函数结合使用。softmax 函数将模型的原始输出转换为概率分布,而交叉熵损失函数则计算这个预测概率分布与真实概率分布之间的差异。这种组合在多分类问题中非常有效。它基于信息论中的交叉熵概念,用于衡量模型预测概率分布与真实标签分布之间的差异。
介绍交叉熵先得从信息量,信息熵再到相对熵说起。热力学中的热熵是表示分子状态混乱程度的物理量。香农用信息熵的概念来描述信源的不确定度。信息是用来消除随机不确定性的,信息量的大小与信息发生的概率成反比。概率越大,包含的信息量越小,概率越小,包含的信息量越大。如“明天太阳从东边升起”,这条信息并没有减少不确定性,因为太阳肯定是从东边升起的,这是一句废话,信息量为0。“明天在天上能看见彩虹”,我们都知道,要想看见彩虹,需要一定条件的,比如要同时有水汽和阳光等,所以从直觉上,这条信息具有一定信息量的。
信息量
设某一件事发生的概率为p(x),其信息量为:I(x) = -log(p(x))
其中I(x)表示信息量,这里log表示以e为底的自然对数,以2为底则表示对应bit数的信息量。
信息熵
信息熵也被称为熵,用于表示某件事可能发生所包含的所有信息量的期望。这个期望的计算方式为每件事发生的概率乘以每件事的信息量之和。可用公式表示为:
比如我们要求得明天天气的信息熵,根据今天天气的情况,我们预测明天是晴天的概率为0.7,明天是雨天的概率是0.1,明天是阴天的概率是0.2,则明天的天气信息熵可计算为:
H(x) = -(0.7xlog(0.7))+0.1xlog(0.1)+0.2xlog(0.2))
相对熵(KL散度)
相对熵或者叫KL散度通常用于衡量同一个随机变量X的两个独立概率分布P(x)与Q(x)之间的差异,可用公式表示为:
由公式可知,当P(x)与Q(x)分布非常接近时,Dkl越接近于零,所以机器学习或者深度学习中可以利用KL散度作为损失函数,通过训练模型的预测分布Q(x),使其慢慢逼近训练数据分布P(x),进而使得两个分布的KL散度值达到最小。
交叉熵
将上面KL散度公式展开:
公式后面的H(p||q)即为分布P(x)与Q(x)的交叉熵,所以:
在机器学习有监督训练网络时,输入数据与标签常常是已经确定好的,所以训练数据的真实概率分布P(x)其实是已知的,那么对应的信息熵H(x)就可以计算出来,是一个常量;前面我们介绍KL散度时已经表明KL散度值表示真实概率分布P(x)与模型预测概率分布Q(x)之间的差异,值越小代表两者差异越小,所以可以把最小化KL散度值当做模型优化的目标,而现在交叉熵等于KL散度值加一个常量(信息熵H(x)),而且交叉熵计算公式更简单,所以用最小化交叉熵代替最小化KL散度作为模型优化的目标函数是现在常用做法。
1.2 标签平滑label smooth
因为标签可能存在错误标注(噪声标签),为了避免过度信任噪声标签而导致模型过拟合,所以提出了标签平滑技术,即将hard label变成soft label,对于ont-hot编码,原来是1的位置变成1-α,其他原来为0的位置变成α/(k-1),α通常取值为0.1,k为类别数量。例如,一个3分类任务,且真实标签为q,预测概率p是由网络最后一层输出经过softmax变换得到,则交叉熵损失可表示为:
对于标签q=[0,1,0]通过标签平滑后,变成q’=[0.05, 0.9, 0.05],原来的交叉熵损失为:
CEori = -log(p1),而通过标签平滑后,交叉熵损失变成了:
CE = -(0.05log(p0)+0.9log(p1)+0.05log(p2))
1.3 Focal loss
Focal loss是在2017年目标检测论文RetinaNet中提出的,用于控制目标检测中正负样本框的平衡问题;RetinaNet指出,在单阶段密集目标检测算法中,例如SSD,有1万到10万个候选框,但是里面有目标的正样本占的比例非常少,剩余的全为负样本。正负样本不平衡会导致两个问题:一是模型学习不高效,可能学习到大量简单的负样本,这对于模型学习没有多大用处。二是简单的负样本会压制模型训练,导致模型能力退化。
Focal Loss是为one-stage的检测器的分类分支服务的,它支持0或者1这样的离散类别label。
目的是解决样本数量不平衡的情况:
1)正样本loss增加,负样本loss减小
2)难样本loss增加,简单样本loss减小
一般分类时,通常使用的交叉熵损失函数如下:
为了解决正负样本不平衡问题,通常在交叉熵损失前面加一个参数α,用于控制对应类别损失的大小。比如负样本多,那就减小负样本前面的参数以降低负样本的权重,正样本少,就增大正样本前面的参数以增加正样本的权重。用公式可表示为:
虽然通过增加参数α可以平衡了正样本/负样本的重要性,但它区分不了简单样本和困难样本,在单阶段目标检测算法中,有大量的简单样本,这就导致损失大部分其实是由简单样本所主导。所以作者提出,要重新构造损失函数以降低简单样本的权重,从而将训练重点放在困难负样本上。
Focal loss认为,易区分的简单样本(即置信度高的样本)对模型学习的贡献小,可以调低它们的权重,模型应该重点关注那些难以区分的困难样本(即置信度低的样本),公式如下:
为了同时平衡正负样本问题,Focal loss还结合了加权交叉熵的参数,所以两者结合后得到了最终的Focal loss为如下公式:
2. 目标定位损失
目标定位损失,用于优化位置和尺寸偏差,是目标检测算法中特有的损失函数,算法最终检测得准不准,很大程度上归功于目标框定位损失设计得好不好。目标框有四个角点一个中心点,早期像YOLOv1检测算法,就是通过直接回归目标框的四个角点得到定位损失的,后面改进到smooth L1,再到IoU损失,进一步出现GIoU,DIoU,CIoU,RIoU,EIoU等变体。
2.1 均方误差MSE(L2损失)
均方误差(Mean Square Error, MSE)通常用于回归损失函数中,它表示预测值f(x)与真实目标值y之间差值平方和的均值,可用如下公式表示:
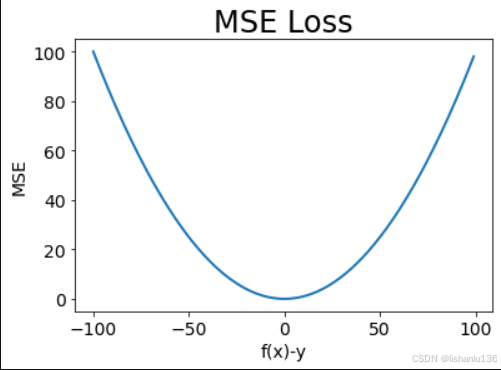
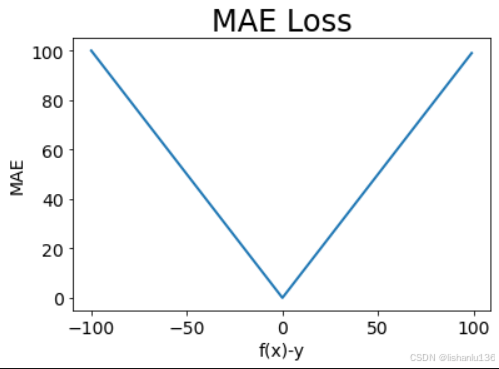
MSE曲线如下图所示,在f(x)等于y时,损失值最小为0。
它的优点是曲线连续光滑,处处可导。缺点是不太稳定,由于平方的原因,会将误差放大,容易受到异常值影响,当函数的输入值(f(x)-y)偏离中心点较远时,梯度会变得非常大,在训练初期不稳定;在接近于真实值的时候即(f(x)-y)值接近于0时,曲线却变得十分的平缓,甚至可能会出现梯度趋向于0的情况,这就造成训练速度变慢。
均方误差在很多地方也被称为L2损失,和误差平方和损失(Sum Square Error, SSE)也是一样的效果。
下图是YOLOv1的损失函数构成:
可以看到YOLOv1的损失由三部分组成,localization loss,objectness loss和classification loss,它们均采用L2损失。
2.2 平均绝对误差MAE(L1损失)
平方绝对误差也是常用于回归的一种损失函数,MAE用于衡量预测值f(x)与真实目标值y的误差绝对值之和,对于一组预测值,通常求它们的平均绝对误差,用下面公式可表示为:
它的导数是常数,当f(x)-y大于0时,导数为1,当f(x)-y小于0时,导数为-1,当f(x)-y等于0时,不可导。
它的优点是拥有稳定的梯度,对于异常值没有L2损失那么敏感,因为MAE计算的是误差的绝对值,对于任意大小的误差,MAE对误差的惩罚都是一样的。缺点是导数为常数,在训练后期,x 很小时(对应上图f(x)-y值很小), 如果学习率不变,损失函数会在最优值附近波动,很难收敛到最优值。MAE也经常被叫做L1损失函数。
2.3 smooth L1
从梯度求解及模型收敛方面考虑,MSE是优于MAE的,因为MSE处处可导,且梯度值是动态变化的,能达到快速收敛的目的。对于异常值敏感度方面考虑,MAE是优与MSE的,它不会由于误差大而加大对异常值的惩罚,从而让模型更新偏向于拟合异常值。结合两者的优势,就是smooth L1了,顾名思义,smooth L1就是平滑的L1损失函数,公式如下:
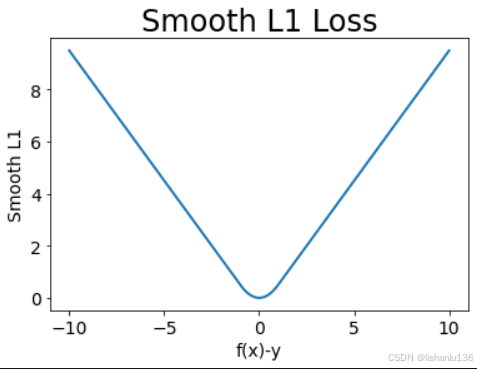
SmoothL1曲线如下图所示,可以看到对比L1损失曲线,在0点处,SmoothL1更平滑,它优化了L1损失函数在0点处不可导的缺点,并保持了L1损失函数对异常值不敏感的优点。
在Fast RCNN的定位损失中作者采用了Smooth L1损失,公式如下:
作者指出,Smooth L1是更鲁棒的L1,相比于R-CNN以及SPPnet中使用的L2损失,当回归目标框无边界时,具有L2损失的训练可能需要仔细调整学习梯度,以防止梯度爆炸。但是Smooth L1由于保持了L1对异常值不敏感的优势,避免了这个问题。
所以Smooth L1相对于L1损失而言,它可以收敛得更快,误差小时,梯度会减小,不会产生震荡;相对于L2损失而言,对于异常值不敏感,梯度变化稳定,训练时不易产生梯度爆炸。
2.4 IoU损失函数
论文:UnitBox: An Advanced Object Detection Network
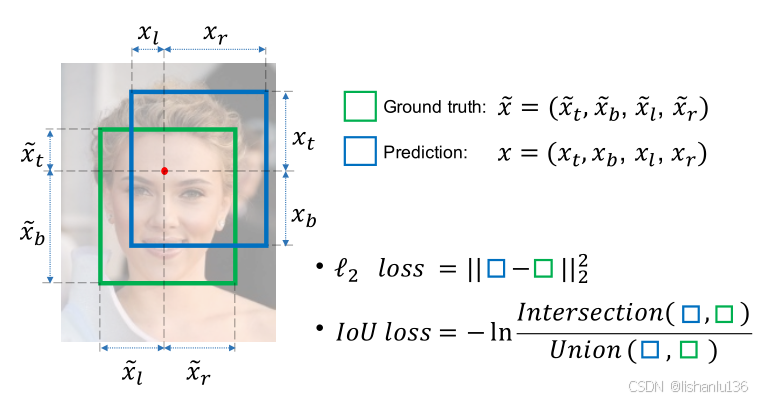
IoU损失首次出现是在2016年的UnitBox论文中,用于人脸检测。作者提到作为对比的DenseBox人脸检测算法利用特征图的每个像素来回归一个4-D的距离向量(当前像素与包含它的候选对象的四个边界之间的距离)。然而,DenseBox采用的L2损失,违背了矩形框四个点是相关的,作者认为应该联合回归。此外,DenseBox为了平衡不同尺度的边界框,还要求将训练图像补丁调整为固定比例。因此,DenseBox必须对图像金字塔进行检测,这不可避免地影响了框架的效率。于是作者提出了更高效的IoU损失函数。两个框的IoU以及L2距离计算方式如下:
因为IoU的大小分布是[0,1]这一特性,所以我们可以把IoU看作是从伯努利分布中一种随机抽样的变量,论文中采用的损失函数是把IoU当做交叉熵的输入:
与L2 loss相比,可以看到IoU loss将边界框视为一个整体变量,而不是像L2 loss那样独立优化四个坐标。
现在用得更多是IoU损失是 LIoU = 1-IoU
IoU代表预测框和真实框的交集与并集之比,当预测框与真实框完全重合时,IoU就等于1,这时LIoU就等于0,优化LIoU,使其越小,说明预测框越来越接近真实框。
总之,IoU损失相对于L2损失有如下优势:
1、L2损失把预测框坐标当做互相独立的四个变量进行训练,而IoU损失将预测框作为一个整体进行训练,这样得到的结果更准确;
2、无论输入的样本是什么样子,IoU的值均介于 [0,1],这种天然的归一化的损失使模型具有更强的处理多尺度图像的能力。
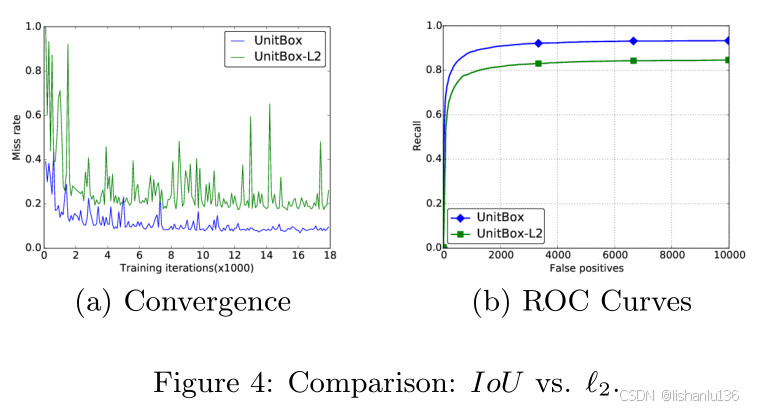
3、相对于L2损失,IoU损失收敛速度更快,相同误识率下,召回率更高,如下图所示:
4、L2损失对多尺度敏感,但IoU损失对于多尺度不敏感。如下图所示:
IoU作为损失函数也存在如下问题:
1、如果预测框和真实框没有重叠,则两者的IoU值为零,这并不能反映两者之间的距离。
2、当两个框不重叠时,IoU损失为1,为常数,则梯度为0,无法进行参数优化更新。
2.5 GIoU损失函数
论文:Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
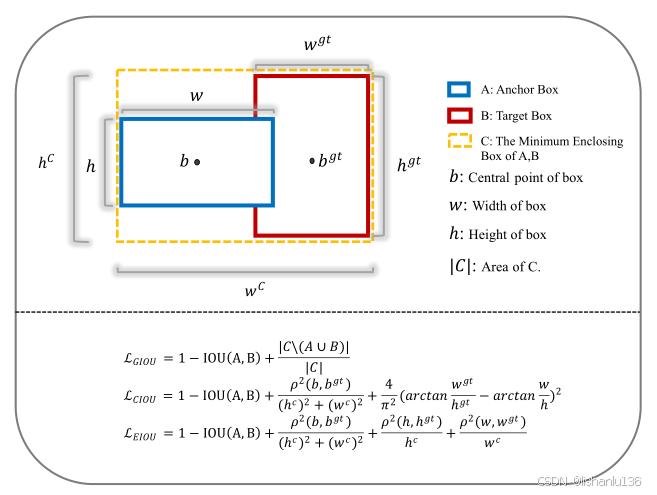
由于IoU作为损失函数存在框不重叠情况下无法优化的问题,所以作者提出了通用IoU损失,即GIoU(Generalized Intersection over Union),使得即使预测框与真实框不重叠的情况下,依然能计算损失,依然能让预测框尽可能朝着真实框的位置移动,GIoU的计算方式如下:
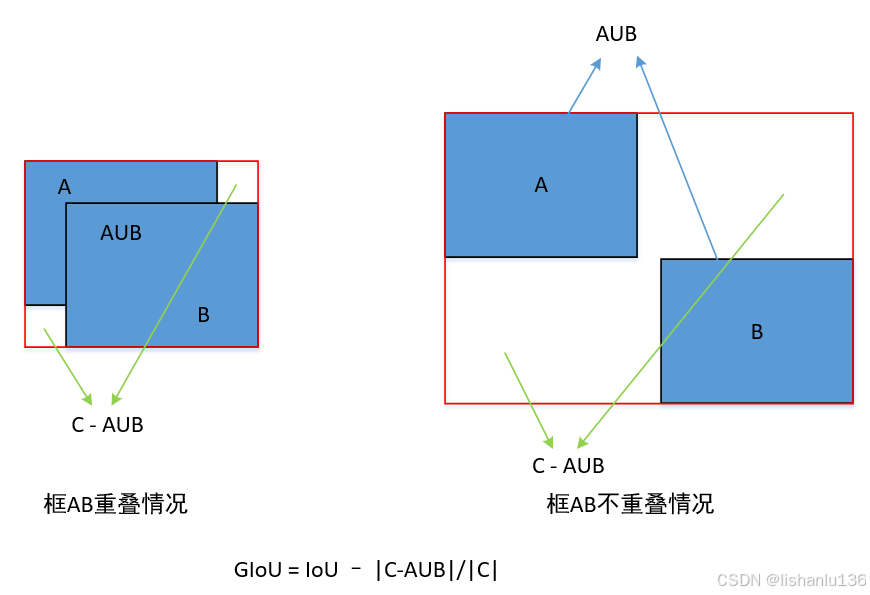
相对于IoU,GIoU需要找出框A与框B的最小闭包矩形框C,当两个框A,B不重叠时,IoU等于0,则可以通过闭包框C和AB并集的差集与闭包框C的比值来计算损失值大小。如下图,各个值代表的区域如下:
上图中红框代表框A与框B的最小闭包框C,GIoU主要解决框AB不重叠情况下,无法更新的问题,可以看到,当框AB不重叠情况下,GIoU = 0-|C-AUB|/|C|,随着,框A与框B的距离越来越远,GIoU会越来越接近-1。所以GIoU不仅可以关注框的重叠区域大小,而且还可以关注其他非重叠区域大小,能较好反映出两个框直接的距离。
GIoU也有不足之处:
1、对每一对预测框与真实框均需要计算最小闭包框,整个计算过程比IoU增加了耗时,而且收敛慢。
2、当一个框完全包含另一个框时,GIoU退化成了IoU,还是不能反映两个框的距离远近。
而GIoU损失,论文参考常用的IoU损失,采用了1-GIoU作为损失函数,即:
LGIoU = 1-GIoU
由于GIoU的范围是[-1, 1],所以GIoU损失LGIoU的取值范围是[0, 2]。
2.6 DIoU损失函数
论文:Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
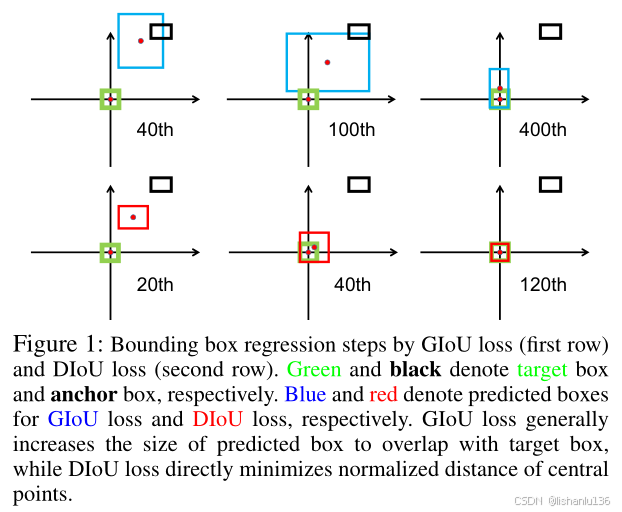
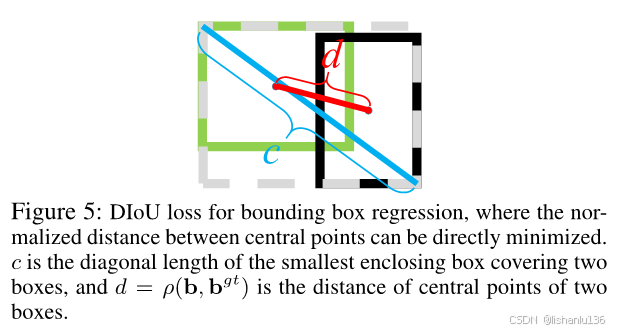
DIoU(Distance-IoU)通过简单地在IoU损失上添加一个惩罚项,直接最小化两个边界框中心点之间的归一化距离,可以得到比GIoU损失更快的收敛速度,如下图所示:
用GIoU loss优化,预测框通常会首先被增大用于覆盖真实框,然后随着迭代次数增加再慢慢减小预测框。而DIoU loss优化是直接最小化两个框中心点的归一化距离。
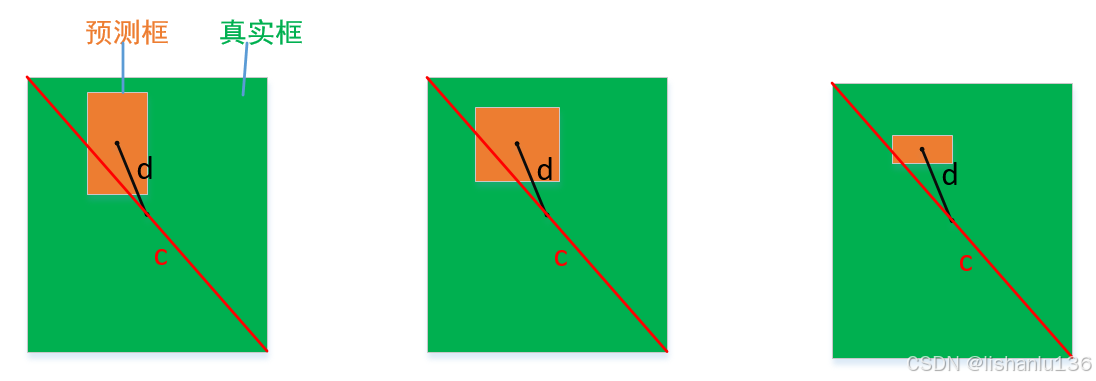
除了收敛快的优点,DIoU还解决了上一节提到的GIoU在两个框存在包含问题时退化成IoU不能体现两者距离的问题,如下图所示:
上图中真实框完全包含预测框时,即使预测框在真实框内部三个不同位置处,IoU大小也是一样的,同样,GIoU此时退化成IoU,其大小也和IoU一样,即两个框存在包含关系时,IoU、GIoU无法体现两个框的位置远近关系。而DIoU却能得到不一样的数值用于体现两个框的位置远近关系。
DIoU也可以应用在NMS中,在抑制冗余预测方面比原有NMS具有更高的鲁棒性。
作者基于IoU损失新增加了一个惩罚项,如下:
其中R(B, Bgt)代表新增加的基于预测框B和真实框Bgt的惩罚项
作者定义的DIoU计算公式为:
其中b和bgt代表预测框B和真实框Bgt的中心点,ρ(.)代表求欧式距离,c代表两个框的最小外接矩形的对角线长度。如下图所示:
所以DIoU损失函数定义如下:
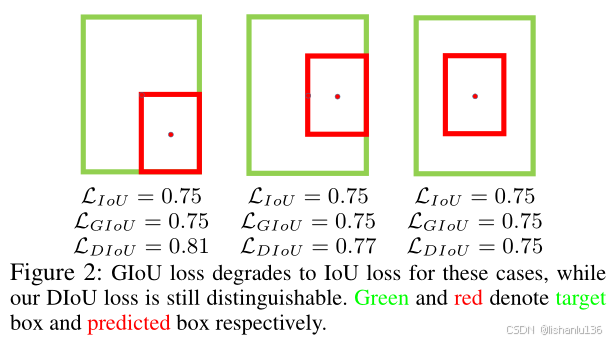
作者认为一个好的边界框回归损失函数应该考虑三个重要的几何因素,即重叠面积、中心点距离和宽高比。通过统一边界框坐标,IoU损失考虑了重叠区域,GIoU损失严重依赖于IoU损失,等同于只考虑了重叠区域。DIoU损失是同时考虑边界框的重叠面积和中心点距离。然而,边界框宽高比的一致性也是一个重要的几何因素,这点DIoU损失没有考虑到,如下图,当预测框在真实框内部,且两者中心点距离一致时,DIoU大小是一样的,这样就无法体现谁回归得好了。
2.7 CIoU损失函数
CIoU损失和DIoU损失是在同一篇论文提出的,是对DIoU损失的一个改进,改进了DIoU损失没有考虑到矩形框宽高比的情况,CIoU的计算公式如下:
可以看到CIoU的计算方式是在DIoU的基础上增加了αν,其中α是一个平衡参数,ν表示宽高比一致性评估指标,其公式如下:
α参数定义如下:
所以CIoU损失函数的计算公式如下:
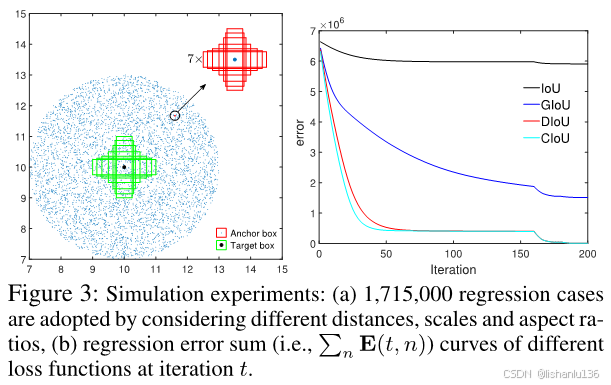
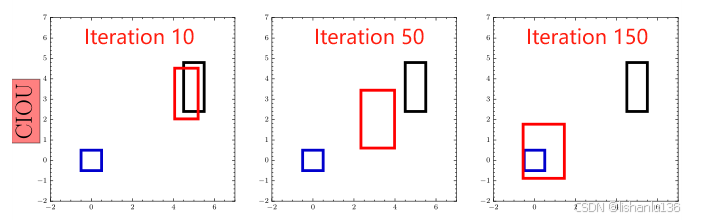
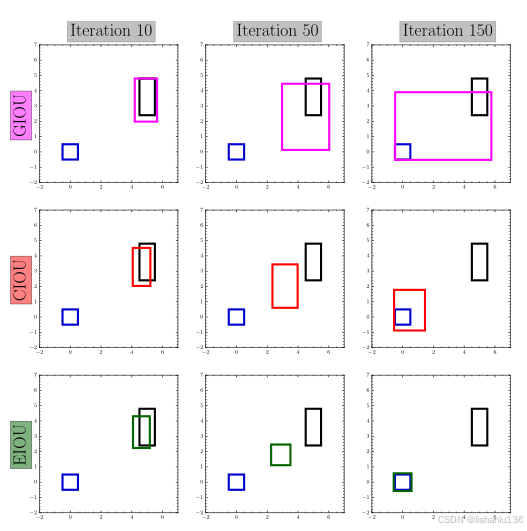
CIoU损失和DIoU损失对比GIoU以及IoU损失可以明显加快收敛速度,如下图,是作者做的实验对比,可以看到CIoU和DIoU在50次迭代就基本收敛到很小的值了,而GIoU和IoU需要迭代大量的次数,IoU迭代200次甚至不能得到一个较小的误差。
作者在论文的实验部分,将YOLOv3,SSD,Faster R-CNN的损失函数由IoU、GIoU替换成DIoU和CIoU以及CIoU with DIoU NMS,结果表明均带来性能提升。
通过αν的公式可以看出,CIoU依然存在不足之处:
1、若预测框和真实框的宽高比相同时,则αν这个新增的惩罚项为0,CIoU将退化成DIoU,存在不合理之处。
2、从论文中给出的ν对w和h的求导公式可以看出,如下图,w和h是一对相反数,无法同时增大或减小,这抑制了模型的优化。
即:
3、由于ν只反映了两个框宽高比的差异,所以CIoU损失可能以不合理的方式优化相似性。比如:CIoU可能只关注两个框之间宽高比的相似性,而忽略两个框实际大小的差异。如下图所示,随着迭代次数增加,预测框(红框)与真实框(蓝框)的距离在拉进,且预测框的宽高比也在逐渐趋近于真实框的宽高比,但是预测框的大小还是没有趋近于真实框的大小,还得通过增加迭代次数进一步优化。
2.8 RIoU损失函数
论文:Single-Shot Two-Pronged Detector with Rectified IoU Loss
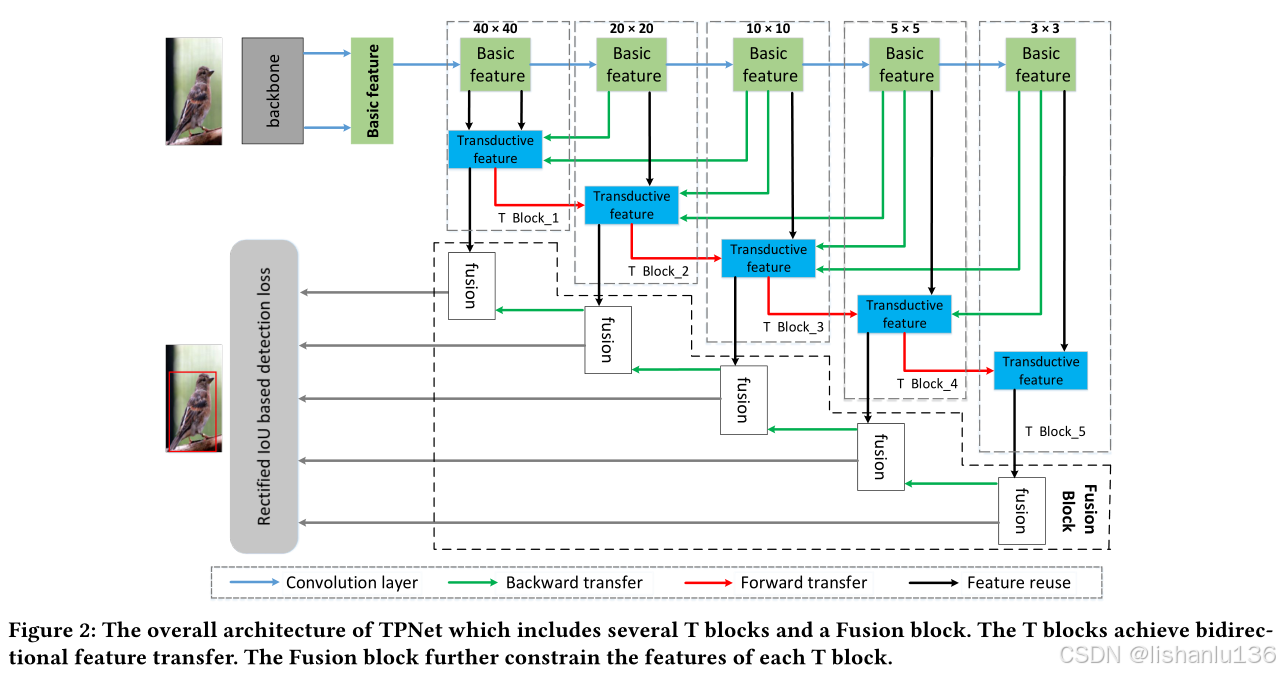
作者在文中指出,现如今的检测算法大多采用特征金字塔用于缓解目标实例间尺度变化的问题。这些目标检测器通过自上而下的路径和横向连接来增强特征,主要是为了丰富底层特征的语义信息,但是忽略了高层特征的增强。这可能导致不同级别特征之间的不平衡,特别是高层级特征中严重缺乏底层详细信息,这使得难以获得准确的边界框。所以作者在网络中引入了双向转换思想,从前向和后向两个方向探索不同层之间的关系,从而丰富了低层特征的语义信息和高层特征的细节信息。作者设计的网络被命名为TPNet( Two-Pronged Network)。
此外,由于单阶段检测器中难易样本的分布不平衡,定位损失梯度往往被定位精度较差的难样本(即IoU小的样本)所主导。这将使模型偏向于学习难样本而导致难以收敛。因此,在TPNet中,提出了一种基于自适应IoU的定位损失,称为RIoU(Rectified IoU)损失,对每一类样本的梯度进行整流。RIoU损失增大了高IoU样本的梯度,抑制了低IoU样本的梯度,从而提高了模型的整体定位精度。
TPNet的整体框架如下,主要包含T block和Fusion block两种模块,作用是促进了低层特征和高层特征的特征融合,这里不展开陈述了。
这里聊聊RIoU损失函数,作者意识到在单阶段中存在大量的难样本,这里的难样本是anchor boxes与真实标注框存在较低的IoU值,大量的难样本会贡献大部分的梯度用来模型优化,这就导致模型训练不稳定,难以收敛的问题。因为IoU值小的困难样本是占大多数的,IoU值大的简单样本只占少部分,作者的想法是直接根据IoU值大小自适应调整样本梯度的贡献量,将简单样本(IoU值大)的梯度增大,让网络更关注这些样本,而将难样本(IoU值小)的梯度抑制。这样会使得每种类型的样本的贡献更均衡,训练过程更高效和稳定。
已知IoU损失函数公式如下:
对IoU求导得到:
从IoU损失函数对IoU求导结果可以看出,IoU损失对IoU值大的简单样本和对IoU值小的困难样本得到的梯度都是一样的,一视同仁,而通常情况下,低IoU值的样本数量大于高IoU值的样本数量。所以在训练阶段,困难样本就会主导localization loss的梯度,进而影响坐标框回归的优化。
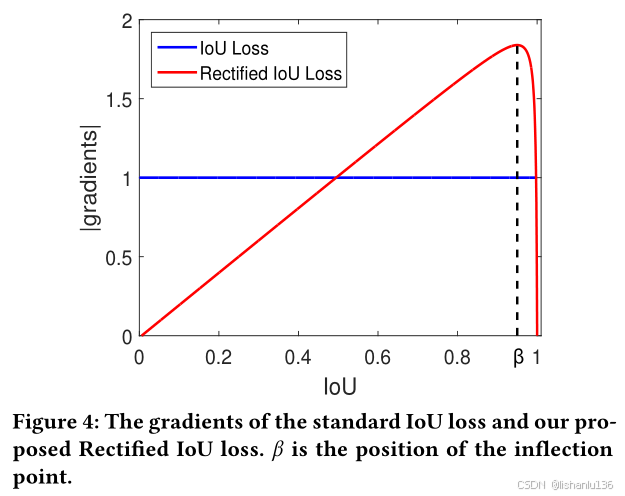
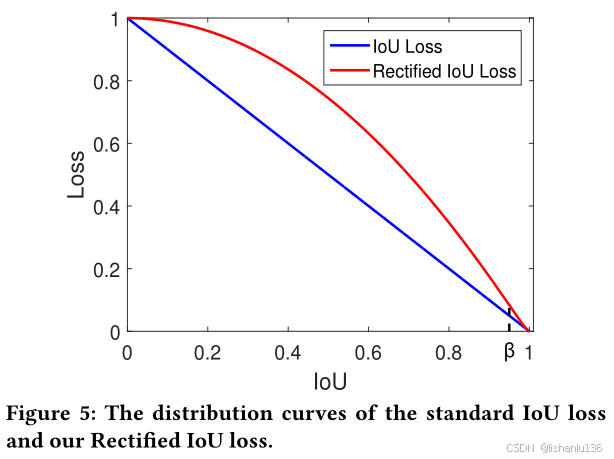
作者的想法是随着IoU值增大,增加样本梯度的权重,但是也不能一味的增大,比如当IoU值为1时,即anchor box与真实框完全重合时,这个时候样本贡献的梯度应该为0。所以,作者给出了IoU值与梯度的关系如下图所示:
上图红色曲线即为RIoU损失的梯度形式,它随着IoU值增加,梯度值也增加,待IoU增大到β后(文中β取值为0.95),梯度值急剧下降。红色曲线是双曲线函数,可通过a,b,c,k四个参数定义如下:
对上式进行积分并结合边框回归损失的性质可得到RIoU损失的公式为:
RIoU与IoU损失曲线如下图所示,当IoU<β时曲线是凸型,当IoU>β时曲线是凹型。
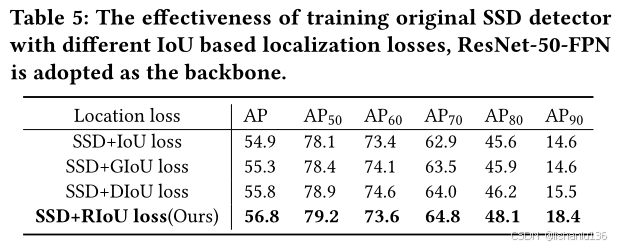
最后作者也在SSD检测算法上验证了RIoU损失函数的效果:
2.9 EIoU与Focal-EIoU损失函数
论文:Focal and Efficient IOU Loss for Accurate Bounding Box Regression
该论文指出现如今边界框回归损失函数存在的两点不足:
1、基于L2范数的损失函数和基于IoU的损失函数都不能有效地描述边界框回归的目标,从而导致收敛缓慢和回归结果不准确。
2、大多数边界框回归损失函数都忽略了样本不平衡问题,因为大部分的anchor boxes与真实框仅有小部分重叠,但是会贡献大部分的边框回归优化梯度,这是不合理的。
EIoU也是同时考虑了重叠面积,中心点距离和宽高比三个因素,公式如下:
其中wc与hc分别代表两个框最小外接矩形C的宽和高,与CIoU损失不同的是,EIoU直接减小了预测框与真实框宽度和高度的差值,使得收敛速度更快,定位效果更好。
下面是GIoU、CIoU、EIoU三个损失函数定义以及迭代收敛速度对比:
可以看到,在迭代150次以内,EIoU能快速收敛到最佳。
和上一节RIoU一样,EIoU的作者也意识到了边框回归中存在的样本不均衡问题,即高质量的IoU值大的样本只占少部分,而大部分均是低质量低IoU值的困难样本,模型更新梯度被大部分低质量样本所主导,作者想提升高质量样本梯度所占的权重,于是提出了Focal-EIoU损失,其公式如下:
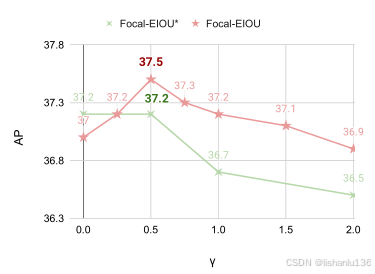
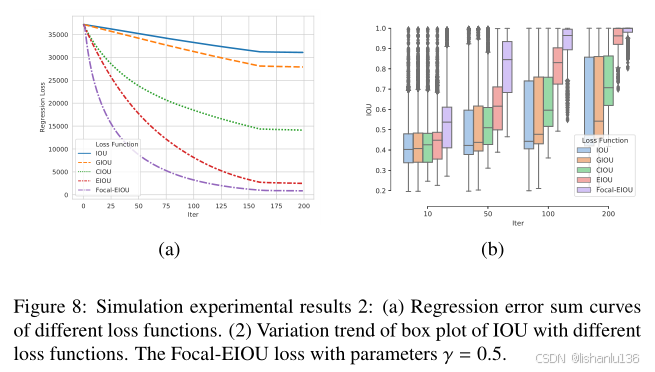
公式中γ是一个超参数,用于控制对低IoU值困难样本的抑制程度,作者做了消融实验得出γ=0.5时,性能最佳,如下图所示。因为IoU值是[0, 1]的小数,γ越大,则IoUγ值越小,且对较小IoU值抑制越强;较大的γ值对困难样本的抑制作用较强,可能会减慢收敛速度。这也是当γ = 2.0时,性能比较差的原因。
下图是各种IoU损失随着迭代次数增加边框回归损失减小和学习样本的分布情况,可以看出,Focal-EIoU收敛最快且随着迭代次数增加,倾向于学习高IoU值的样本。
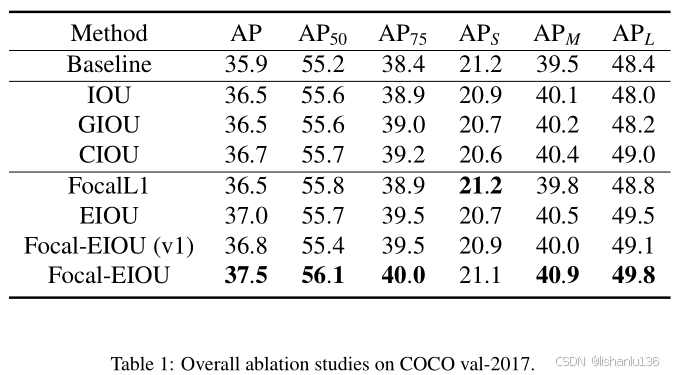
下表是作者基于RetinaNet(ResNet-50+FPN)为基准,评估各个IoU损失的消融实验:
2.10 α-IoU损失函数
论文:Alpha-IoU: A Family of Power Intersection over Union Losses for Bounding Box Regression
作者将现有IoU损失推广到一个更加通用的IoU损失,通过添加一个参数α参数作为IoU的指数项用于对整个IoU损失添加正则的效果。公式如下:
可以看出,通过调节α参数,可以调节不同质量的样本对损失梯度的贡献程度,使得在选取样本重心时更加灵活,并且,作者也通过实验证明α-IoU对带噪声的小数据集更加鲁棒。
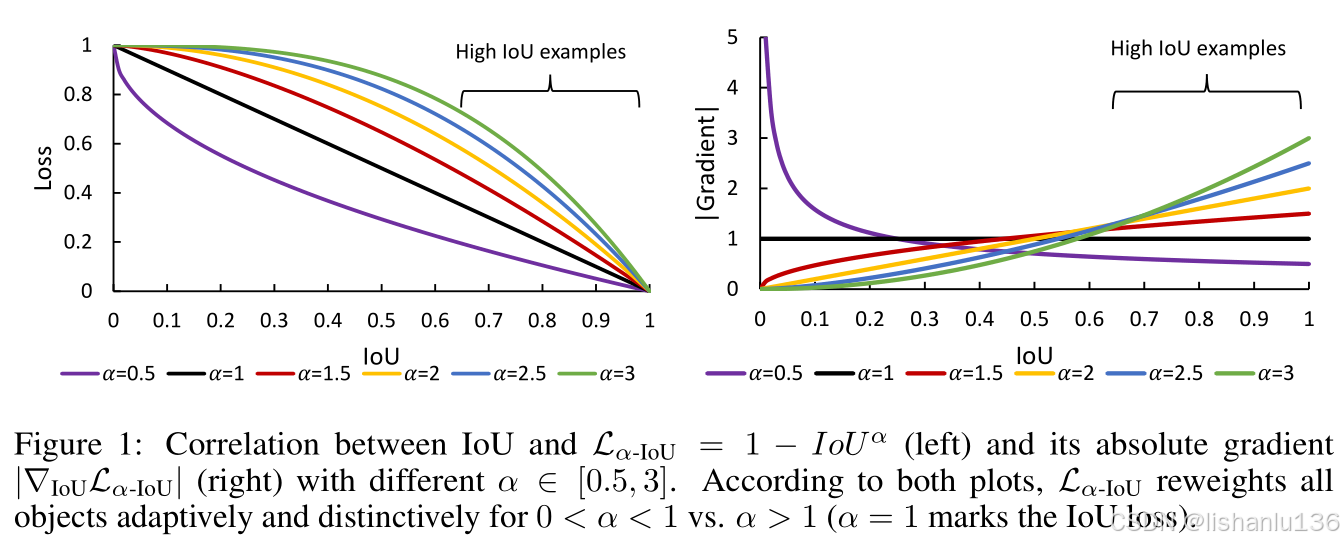
比如:当设置α > 1时,Lα-IoU提高了高IoU样本的损失和梯度,从而提高了bbox回归的精度。当0 < α < 1时,Lα-IoU会降低高IoU样本的权重,这会影响bbox回归的准确性。参数α可以作为调节α-IoU损失的旋钮,以满足不同IoU值样本对bbox回归的贡献量,α > 1是高回归精度(即高IoU阈值),更多地关注那些高IoU样本,实验中,作者得出的结论是α=3结果最好,并且对数据集不敏感。
α-IoU损失本质上还是和RIoU损失,EIoU损失一样的效果,通过样本的IoU值大小来自适应调整该样本对损失和梯度的权重。但是文中指出RIoU和EIoU公式不简洁并且不一般化,作者所提的α-IoU损失只需调整一个α参数就可以自适应按样本IoU值大小重新分配它们对损失和梯度的权重。
下图是标准IoU损失与不同α值下(α取0.5到3)的α-IoU损失值与梯度值曲线对比图:
利用上述α-IoU损失公式,作者还把它推广到GIoU、DIoU、CIoU损失,如下: