分组密码的整体结构

转载地址：http://hi.baidu.com/xiaoheng199110/item/cca9beb342528e482aebe31f

扩散(diffusion)和混淆(confusion)是C.E.shannon提出的设计密码体制的两种基本方法，其目的是为了抵抗对手对密码体制的统计分析。在分组密码的设计中，充分利用扩散和混淆，可以有效地抵抗对手从密文的统计特性推测明文或密钥。扩散和混淆是现代分组密码的设计基础。

所谓扩散就是让明文中的每一位影响密文中的许多位，或者说让密文中的每一位受明文中的许多位的影响，这样可以隐蔽明文的统计特性。当然，理想的情况是让明文中的每一位影响密文中的所有位，或者说让密文中的每一位受明文中的所有位的影响。

所谓混淆就是让密文与密钥之间的统计关系变得尽可能复杂，使得对手即使获取了关于密文的一些统计特性，也无法推测出密钥。使用复杂的非线性代替变换可以达到比较好的混淆效果，而简单的线性代替变换得到的混淆效果则不理想。可以用“揉面团”来形象地比喻扩散和混淆，当然，这个"揉面团"的过程应该是可逆的．乘积和迭代有助于实现扩散和混淆．选择某些较简单的受密钥控制的密码变换，通过乘积和迭代可以取得比较好的扩散和混淆的效果。

现代的分组密码体制主要有两种结构：Feistel网络和SP网络。

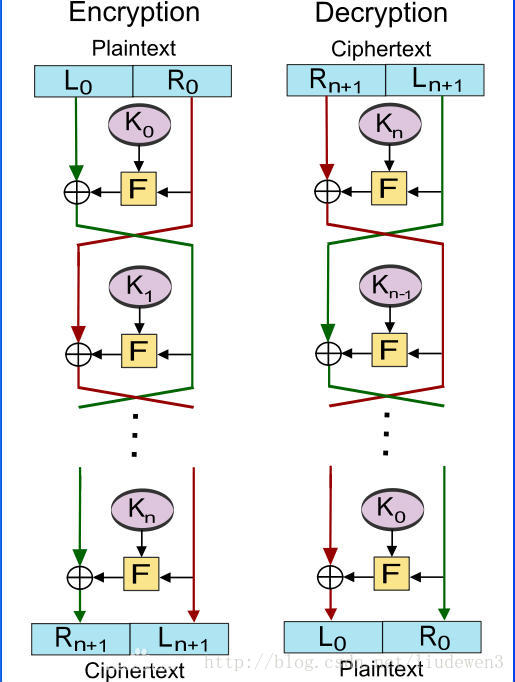
Feistel网络的典型代表是DES算法。Feistel网络的主要过程如下：

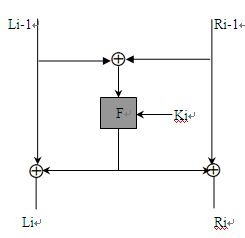
加密过程：令F为轮函数，另K1，K2，……，Kn 分别为第1，2，……，n 轮的子密钥。那么基本构造过程如下：

将明文信息均分为两块：(L0，R0)；

在每一轮中，进行如下运算(i 为当前轮数)：Li+1 = Ri；Ri+1 = Li ⊕F (Ri，Ki)。(其中⊕为异或操作)所得的结果即为：(Rn+1，Ln+1)。

解密过程：对于密文(Rn+1，Ln+1)，我们将i 由n 向0 进行，即， i = n，n-1，……，0。然后对密文进行加密的逆向操作，如下：

Ri = Li+1;

Li = Ri+1⊕F (Li+1，Ki)。(其中⊕为异或操作)

所得结果为(L0，R0)，即原来的明文信息。

Feistel网络的流程图如下所示：

SP网络(substitution-permutation network)也是一种有效的迭代密码体制，其中的典型代表就是AES算法。给出明文密文分组长度、密钥长度和迭代轮数，根据密钥定义每一轮的密钥Kr，则每一轮我们需要进行两种操作S和P，S操作（S-box）就是代换操作，S-box的最基本的性质是其非线性映射，S-box的输出不能通过对输入的线性变换而得到，从而使密文与加密密钥之间的统计关系复杂化，也就是使明文与密钥充分混合在一起，以致几乎无法从密文提取出明文或密钥的信息；P操作置换操作，就是利用置换函数让明文的统计特征消散在密文中，让明文的每一比特影响尽可能多的密文比特。在上述操作中，代换起到的是混淆作用，置换起到的就是扩散作用，SPN通过代--置换的多次迭代很好的实现混淆与扩散。SP网络的结构图如下所示：

Lai-Massey结构是Lai和Massey设计IDEA算法时候提出的一种结构，另外FOX算法使用的也是这种结构。对于长度为2n的r轮Lai-Massey结构密码，加密流程主要如下描述：

给定2n比特的明文P，首先将其分成左右两个n比特部分，L0R0=P。根据如下规则进行r轮的运算：T=F(L[i-1]⊕R[i-1],Ki);Li=L[i-1]⊕T;Ri=R[i-1]⊕T。Lai-Massey结构加密示意图如下所示：

整体结构是分组密码的重要特征，不同的结构对轮函数的先去以及各种平台的性能都有很大的影响。除了以上三种主流结构之外，还有很多其他的结构，或者以上三种结构的整合等。

分组密码的整体结构

悦读