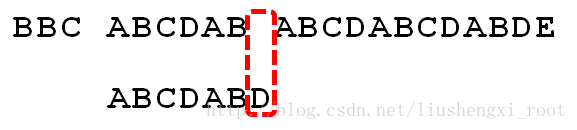什么是模式匹配?
给定一个子串,要求在某个字符串中找出与该子串相同的所有子串,这就是模式匹配。也就是我们平常在记事本中的“查找选项”所运用的算法,其实说白了就是让我们编程实现:在一个大的字符串中找到一个小的字符串并返回其第一个匹配字符的下标
BF算法
时间复杂度为O(m×n),m和n分别是模式串与主串的长度。
思路:将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和 T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果
代码实现:
#include<stdio.h>
#include<string.h>
#include<iostream>
#define MAX 255
using namespace std ;
typedef struct {
int count ;
char str[MAX];
}PP ;
int BF(PP S ,PP T, int pos )
{
int i = pos; // i 指向主串
int j = 1; // j 指向模式串
while(i <= S.count && j<= T.count)
{
if( S.str[i] == T.str[j]){
i++ ;
j++ ;
}
else { //不匹配时,就让T的第一个字符与S的第二个字符进行比较
j= 1 ;
i = i-j + 2 ;
}
}
if(j > T.count) // j大于长度时,就是成功匹配,返回第一个字符在主串中的下标,即i-T.count
return i-T.count;
else
return 0;
}
int main(void)
{
PP S,T ;
S.str[0]=' ';
T.str[0]=' ';
cout << "请输入主串:" << endl ;
scanf("%s",&S.str[1]);
cout << "请输入模式匹配串:" << endl ;
scanf("%s",&T.str[1]);
S.count = strlen(S.str)-1;
T.count = strlen(T.str)-1;
printf("S.str==%s\n",S.str) ;
printf("S.count ==%d\n",S.count);
printf("T.str==%s\n",T.str);
printf("T.count ==%d\n",T.count);
int pos ;
cout << "请输入模式匹配串要在主串的何处开始匹配查找 :" << endl ;
scanf("%d",&pos);
cout << BF(S,T,pos) << endl ;
}
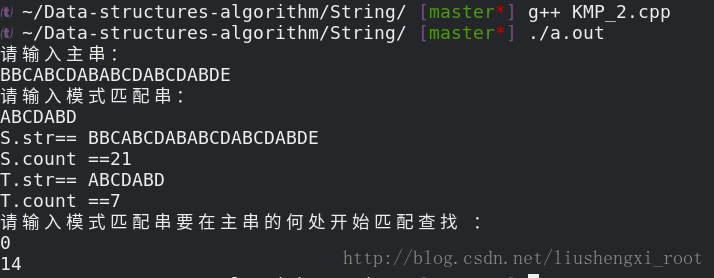
运行截图:
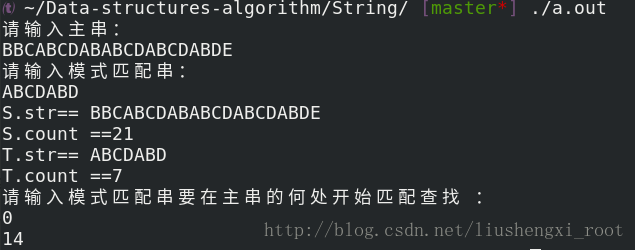
14: 即为T串在S串中第一个匹配字符的下标
讨论:BF算法到底差在哪里?
当我们做到这一步的时候,其实我们已经知道在那个不匹配的字符的前面就是ABCDAB了(其实还应该包含那个不匹配的字符),那么如果按照BF算法的思想,我们还是会去一个一个的去比较。这里就会造成计算效率的低下。那么我们能不能让模式串移动的位数更多一点呢?这个就是KMP算法所做的事情了。
KMP算法
复杂度为O(m+n),是不是很强!!!
next数组是用来干嘛的?
next数组的值,就是下次往前移动字符串T的移动距离。比如next中某个字符对应的值是4,则在该字符后的下一个字符不匹配时,可以直接移动往前移动 T 5个长度,再次进行比较判别。
KMP算法的实现
代码实现:
#include<stdio.h>
#include<string.h>
#include<iostream>
#define MAX 255
using namespace std ;
typedef struct {
int count ;
char str[MAX];
}PP ;
void get_next(PP T , int *next)
{
int after , front;
after= 1; // 表示后缀
front= 0; // 表示前缀
next[1]= 0;
while(after <= T.count )
{
if( front== 0 || T.str[after] == T.str[front]){
after++;
front++;
next[after] = front;
}
else {
//front 回溯,关键点
front=next[front];
}
}
}
// 返回字串T 在主串S中的位置,不存在返回 0
int index_kmp(PP S ,PP T, int pos )
{
int i = pos;
int j = 1;
int next[MAX] ;
get_next(T,next);
while(i <= S.count && j<= T.count)
{
if( j == 0 || S.str[i] == T.str[j]){
i++ ;
j++ ;
}
else {
j=next[j]; //改变 j 就是在移动 T 模式串
}
}
if(j > T.count)
return i-T.count;
else
return 0;
}
//前缀是固定的,二后缀是相对的
int main(void)
{
PP S,T ;
S.str[0]=' ';
T.str[0]=' ';
cout << "请输入主串:" << endl ;
scanf("%s",&S.str[1]);
cout << "请输入模式匹配串:" << endl ;
scanf("%s",&T.str[1]);
S.count = strlen(S.str)-1;
T.count = strlen(T.str)-1;
printf("S.str==%s\n",S.str) ;
printf("S.count ==%d\n",S.count);
printf("T.str==%s\n",T.str);
printf("T.count ==%d\n",T.count);
int pos ;
cout << "请输入模式匹配串要在主串的何处开始匹配查找 :" << endl ;
scanf("%d",&pos);
cout << index_kmp(S,T,pos) << endl ;
}