文章目录
二叉树的遍历
0. 树的表示
typedef struct TreeNode *BinTree;
struct TreeNode{
int Data; // 存值
BinTree Left; // 左儿子结点
BinTree Right; // 右儿子结点
};
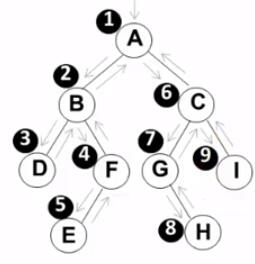
1. 先序遍历
遍历过程:
- 访问根结点
- 先序遍历其左子树
- 先序遍历其右子树
1. 递归实现
void PreOrderTraversal(BinTree BT){
if(BT){
printf("%d",BT->Data); // 打印根
PreOrderTraversal(BT->Left); // 进入左子树
PreOrderTraversal(BT->Right); // 进入右子树
}
}
2. 非递归实现
void PreOrderTraversal(BinTree BT){
BinTree T = BT;
Stack S = CreateStack(); // 创建并初始化堆栈 S
while(T || !IsEmpty(S)){ // 当树不为空或堆栈不空
while(T){
Push(S,T); // 压栈,第一次遇到该结点
printf("%d",T->Data); // 访问结点
T = T->Left; // 遍历左子树
}
if(!IsEmpty(S)){ // 当堆栈不空
T = Pop(S); // 出栈,第二次遇到该结点
T = T->Right; // 访问右结点
}
}
}
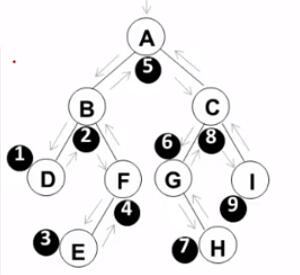
2. 中序遍历
递归过程:
- 中序遍历其左子树
- 访问根结点
- 中序遍历其右子树
1. 递归实现
void InOrderTraversal(BinTree BT){
if(BT){
InOrderTraversal(BT->Left); // 进入左子树
printf("%d",BT->Data); // 打印根
InOrderTraversal(BT->Right); // 进入右子树
}
}
2. 非递归实现
void InOrderTraversal(BinTree BT){
BinTree T = BT;
Stack S = CreateStack(); // 创建并初始化堆栈 S
while(T || !IsEmpty(S)){ // 当树不为空或堆栈不空
while(T){
Push(S,T); // 压栈
T = T->Left; // 遍历左子树
}
if(!IsEmpty(S)){ // 当堆栈不空
T = Pop(S); // 出栈
printf("%d",T->Data); // 访问结点
T = T->Right; // 访问右结点
}
}
}
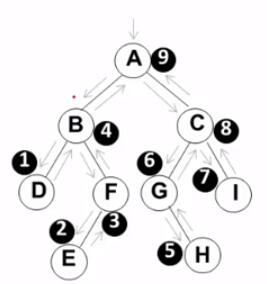
3. 后序遍历
遍历过程:
- 后序遍历其左子树
- 后序遍历其右子树
- 访问根结点
1. 递归实现
void PostOrderTraversal(BinTree BT){
if(BT){
PostOrderTraversal(BT->Left); // 进入左子树
PostOrderTraversal(BT->Right); // 进入右子树
printf("%d",BT->Data); // 打印根
}
}
2. 非递归实现
void PostOrderTraversal(BinTree BT){
BinTree T = BT;
Stack S = CreateStack(); // 创建并初始化堆栈 S
vector<BinTree> v; // 创建存储树结点的动态数组
Push(S,T);
while(!IsEmpty(S)){ // 当树不为空或堆栈不空
T = Pop(S);
v.push_back(T); // 出栈元素进数组
if(T->Left)
Push(S,T->Left);
if(T->Right)
Push(S,T->Right);
}
reverse(v.begin(),v.end()); // 逆转
for(int i=0;i<v.size();i++) // 输出数组元素
printf("%d",v[i]->Data);
}
4. 总结
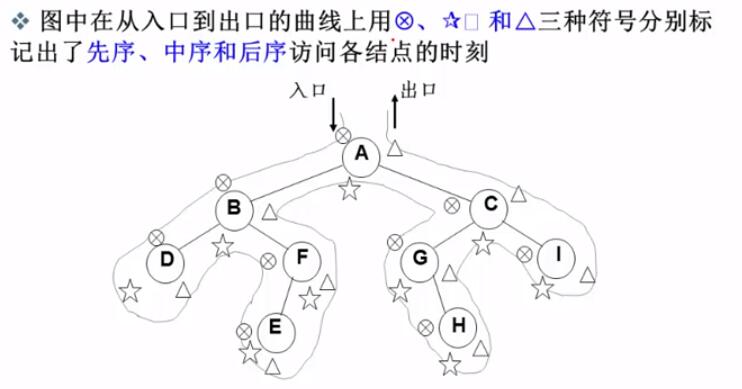
先序、中序和后序遍历过程:遍历过程中经过结点的路线一样,只是访问各结点的时机不同,即:
- 先序遍历是第一次"遇到"该结点时访问
- 中序遍历是第二次"遇到"该结点(此时该结点从左子树返回)时访问
- 后序遍历是第三次"遇到"该结点(此时该结点从右子树返回)时访问
5. 层序遍历
遍历过程:从上至下,从左至右访问所有结点
队列实现过程:
- 根结点入队
- 从队列中取出一个元素
- 访问该元素所指结点
- 若该元素所指结点的左孩子结点非空,左孩子结点入队
- 若该元素所指结点的右孩子结点非空,右孩子结点入队
- 循环 1 - 4,直到队列中为空
void LevelOrderTraversal(BinTree BT){
queue<BinTree> q; // 创建队列
BinTree T;
if(!BT)
return;
q.push(BT); // BT 入队
while(!q.empty()){
T = q.front(); // 访问队首元素
q.pop(); // 出队
printf("%d",T->Data);
if(T->Left) // 如果存在左儿子结点
q.push(T->Left); // 入队
if(T->Right)
q.push(T->Right);
}
}
6. 例子
1. 输出叶子结点
前序遍历加个没有孩子结点的约束即可
void FindLeaves(BinTree BT){
if(BT){
if( !BT->Left && !BT->Right)
printf("%d",BT->Data); // 打印叶子结点
FindLeaves(BT->Left); // 进入左子树
FindLeaves(BT->Right); // 进入右子树
}
}
2. 树的高度
当前树的高度为其子树最大高度 +1
int GetHeight(BinTree BT){
int hl,hr,maxh;
if(BT){
hl = GetHeight(BT->Left); // 求左子树高度
hr = GetHeight(BT->Right); // 求右子树高度
maxh = (hl>hr)?hl:hr;
return maxh+1; // 当前结点高度为左右子树最大的高度+1
}else
return 0;
}
3. 由两种遍历序列确定二叉树
前提:有一种序列必须是中序!
方法:
- 根据先序(或后序)遍历序列第一个(或最后一个)结点确定根结点
- 根据根结点在中序序列中分割出左右两个子序列
- 对左子树和右子树分别递归使用同样的方法继续分解
例如:
前序:ABCDEFG
中序:CBDAFEG
先序遍历为"根左右",则 A 是根,对应可以划分出中序中:(CBD)A(FEG),CBD 为左子树,FEG 为右子树,再根据前序的 BCD,B 为根,划分出中序中 (C(B)D)A(FEG),则 C D 分别是 B 的左右子树…最后可得树为:
A
/ \
B E
/ \ / \
C D F G