从动力学角度看优化算法:从 GD 到 SGD
非常感谢苏老师,原文地址:https://kexue.fm/archives/5655
本文内容主要来自于苏老师的博客,笔者记录下一些问题和想法,有任何问题敬请批评指正,也欢迎留言讨论
梯度下降
训练目标分析
首先,为了要判断不同优化器之间的优越性,我们要明确,梯度下降的终极目标是什么:
假设全部训练样本的集合为
S
S
S,损失度量
L
(
x
;
θ
)
L(x;\theta)
L(x;θ),其中
x
x
x表示单个样本,
θ
\theta
θ是优化参数,那么我们可以构建下面的损失函数:
L
(
θ
)
=
1
∣
S
∣
∑
x
∈
S
L
(
x
;
θ
)
(1)
L(\theta)=\frac{1}{|S|}\sum_{x \in S }L(x;\theta) \tag{1}
L(θ)=∣S∣1x∈S∑L(x;θ)(1)
我们进行训练的最终目标,则是找到
L
(
θ
)
L(\theta)
L(θ)的一个全局最优点,(这里的最优就是损失函数最小的意思)这里大概也是不考虑过拟合和欠拟合的情况
GD 与 ODE(梯度下降 与 常微分方程)
为了完成这个目标,我们可以使用梯度下降法(gradient descent, GD):
θ
n
+
1
=
θ
n
−
γ
∇
θ
L
(
θ
n
)
(2)
\theta_{n+1} = \theta_{n} - \gamma\nabla_\theta L(\theta_{n}) \tag{2}
θn+1=θn−γ∇θL(θn)(2)
公式
(
2
)
(2)
(2)是梯度下降法的一个表示,其中:
θ
n
\theta_n
θn指的是
n
n
n次迭代时的参数值,
γ
>
0
\gamma\gt 0
γ>0是指学习率;
∇
θ
L
(
θ
n
)
\nabla_\theta L(\theta_n)
∇θL(θn)表示损失函数
L
(
θ
)
L(\theta)
L(θ)在
θ
n
\theta_n
θn处的梯度。(实际上,梯度类似于 ”坡度“,梯度的方向指示了往哪个方向变化最快;梯度的大小反映了坡度的大小,也可以说是反映了变化的快慢)
关于 γ \gamma γ,苏老师提到:这里的 γ \gamma γ 刚好是迭代的步长,但是后面我们可以看到,步长不一定等于学习率。
下面是梯度下降的其中一种理解方法,因为一般
γ
≪
1
\gamma \ll 1
γ≪1,这里我们把公式
(
2
)
(2)
(2)变形,可以得到:
θ
n
+
1
−
θ
n
γ
=
−
∇
θ
L
(
θ
n
)
(3)
\frac{\theta_{n+1}-\theta_{n}}{\gamma}=-\nabla_\theta L(\theta_n) \tag{3}
γθn+1−θn=−∇θL(θn)(3)
那么左边就近似于
θ
\theta
θ的导数(假设它是时间
t
t
t 的导数),于是我们可以得到ODE动力系统:
θ
˙
=
−
∇
θ
L
(
θ
)
(4)
\dot \theta=-\nabla_\theta L(\theta) \tag{4}
θ˙=−∇θL(θ)(4)
而
(
2
)
(2)
(2)则是
(
4
)
(4)
(4)的一个欧拉解法。这样一来,梯度下降实际上就是用欧拉解法去求解动力系统
(
4
)
(4)
(4)。
直接给出的结论:由于 ( 4 ) (4) (4)是一个保守动力系统,因此它可以收敛到一个不动点(让 θ ˙ = 0 \dot \theta = 0 θ˙=0),并且可以证明稳定的不动点是一个极小值点(但极小值不代表全局最小)。
可能涉及到了数值计算的相关知识?
来自deep seek 和 kimi 的一种直观解释:
想象你在一个山谷中,山谷的地形就是损失函数 L ( θ ) L(\theta) L(θ)。你每一步都沿着最陡的下坡方向走(负梯度方向),最终你会走到一个山谷底部(极小值点)。但由于山谷可能有多个低点,你可能会走到一个局部最低点,而不是整个山谷的最低点(全局最小)。
从 GD 到 SGD(从梯度下降 到 随机梯度下降)
(
2
)
(2)
(2)我们一般称为“全量梯度下降”,他需要所有样本来计算梯度,那么当样本数量成千上万的时候,每迭代一次的成本都太大。于是,我们考虑每次随机从样本集合
S
S
S中随机抽取一个子集
R
⊆
S
R \subseteq S
R⊆S,然后用
R
R
R来计算梯度并完成单次迭代。我们记:
L
R
(
θ
)
=
1
∣
R
∣
∑
x
∈
R
L
(
x
;
θ
)
(5)
L_R(\theta)=\frac1{|R|}\sum_{x \in R} L(x;\theta) \tag{5}
LR(θ)=∣R∣1x∈R∑L(x;θ)(5)
那么,公式
(
2
)
(2)
(2)就会变为:
θ
n
+
1
=
θ
n
−
γ
∇
θ
L
R
(
θ
n
)
\theta_{n+1} = \theta_n - \gamma \nabla_\theta L_R (\theta_n)
θn+1=θn−γ∇θLR(θn)
注意,
L
L
L的最小值才是我们的最终目标,而
L
R
L_R
LR则是一个随机变量,
∇
θ
L
R
(
θ
n
)
\nabla_\theta L_R (\theta_n)
∇θLR(θn)只是
∇
θ
L
(
θ
n
)
\nabla_\theta L (\theta_n)
∇θL(θn)的一个估计,这样做的正确性和有效性这里还是不显然的。
从 SGD 到 SDE(从 随机梯度下降 到 随机微分方程)
这里我们假设:
∇
θ
L
(
θ
n
)
−
∇
θ
L
R
(
θ
n
)
=
ξ
n
(7)
\nabla_\theta L (\theta_n) - \nabla_\theta L_R (\theta_n) = \xi_n \tag{7}
∇θL(θn)−∇θLR(θn)=ξn(7)
我们假设随机变量
ξ
n
\xi_n
ξn 服从方差为
σ
2
\sigma ^ 2
σ2的正态分布,这个假设比较强,但只是一个近似描述,主要是为了版定性、半定量分析。经过这样的假设,随机梯度下降相当于再动力系统
(
4
)
(4)
(4)引入了高斯噪声,将
(
7
)
(7)
(7)代入
(
3
)
(3)
(3),变形就可以得到:
θ
˙
=
−
∇
θ
L
(
θ
)
+
σ
ξ
(8)
\dot \theta = - \nabla_\theta L(\theta) + \sigma \xi \tag{8}
θ˙=−∇θL(θ)+σξ(8)
其中的
ξ
\xi
ξ 服从标准正态分布(正态分布的线性变换性质)。
原来的动力系统是一个ODE,现在变成了SDE(随机微分方程),我们称之为“朗之万方程”。当然,其实噪声的来源不仅仅是随机子集带来的估算误差,每次迭代的学习率大小也会带来噪声。
关于每次迭代的学习率大小会影响噪声,后面还会提到;个人的理解是当学习率较大的时候,可能会导致在错误的梯度上走较多的距离,也就偏离了原本的梯度,也就引入了误差
我们关注
(
8
)
(8)
(8)对应的随机微分方程,并与
(
4
)
(4)
(4)对应的微分方程进行比较,这两者得到的解是不相同的,甚至在形式上也不同。
(
4
)
(4)
(4)的解是一条确定的轨线,而
(
8
)
(8)
(8)由于引入了一个随机噪声,因此解也是随机的。
对于
(
4
)
(4)
(4),当我们给出相同的初始条件时,一定可以得到相同的结果;
但是对于
(
8
)
(8)
(8),解是随机的,可以解得平衡状态的概率分布为:
P
(
θ
)
∼
exp
(
−
L
(
θ
)
σ
2
)
(9)
P(\theta) \sim \exp(-\frac{L(\theta)}{\sigma^2}) \tag{9}
P(θ)∼exp(−σ2L(θ))(9)
关于
(
9
)
(9)
(9),这里给出一些直观的解释:
最终的平衡状态
θ
\theta
θ 是一个随机变量,且
L
(
θ
)
L(\theta)
L(θ) 越小,
θ
\theta
θ在此处的概率越大;也可以说,损失越小的地方,
θ
\theta
θ 取到的概率越高。
当
σ
\sigma
σ 很大的时候,相当于抹平了不同损失
L
(
θ
)
L(\theta)
L(θ)下的差异,这样
θ
\theta
θ 就会更接近于均匀分布。
结果启发
从 ( 8 ) , ( 9 ) (8),(9) (8),(9)式中我们可以得到一些有意义的结果。首先我们看到,原则上来说这时候的 θ \theta θ 已经不是一个确定值,而是一个概率分布,而且原来 L ( θ ) L(\theta) L(θ) 的极小值点,刚好现在变成了 P ( θ ) P(\theta) P(θ)的极大值点。这说明如果我们无限长地执行梯度下降的话,理论上 θ \theta θ 能走遍所有可能的值,并且在 L ( θ ) L(\theta) L(θ) 的各个“坑”(也就是极小值)中的概率更高。
σ 2 \sigma^2 σ2是梯度的方差,显然这个方差是取决于batch size的。
这里有一些直观的理解,就是 bathch size 越大,取出的样本分布与总体分布就越接近,这个随机变量的方差就会减少
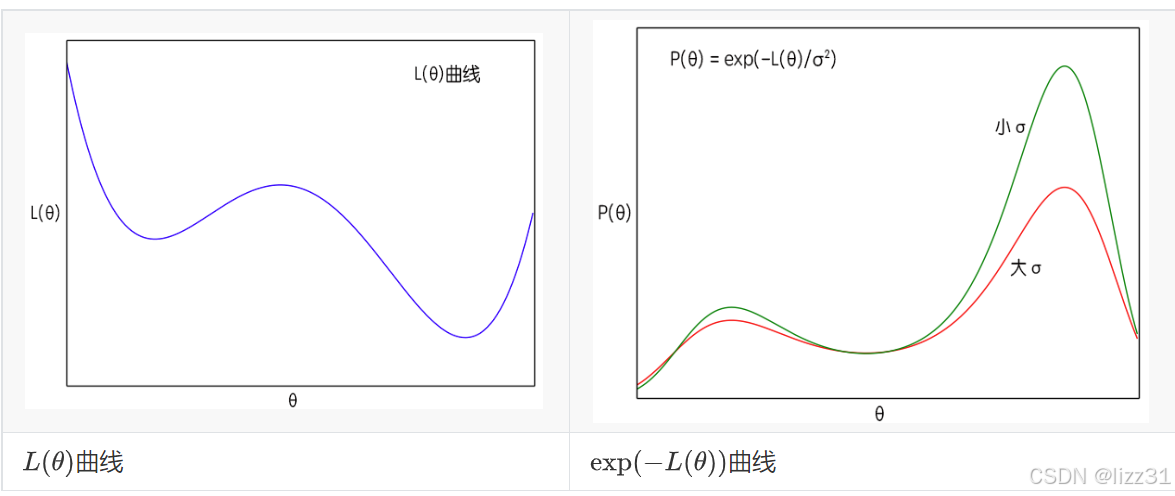
根据定义 ( 7 ) (7) (7),batch size越大方差越小。而在 ( 9 ) (9) (9)式中, σ 2 \sigma^2 σ2越大,说明 P ( θ ) P(\theta) P(θ) 的图像越平缓,即越接近均匀分布,这时候 θ \theta θ 可能就到处跑;当 σ 2 \sigma^2 σ2 越小时,原来 L ( θ ) L(\theta) L(θ) 的极小值点的区域就越突出,这时候 θ \theta θ 就可能掉进某个“坑”里不出来了。图中给出了不同大小 σ \sigma σ 的曲线图,右侧的图由左侧生成,左图函数越小,对应右图 θ \theta θ 取到的概率越大。
这样分析的话,**理论上来说,我们一开始要让batch size小一些,那么噪声方差 σ 2 \sigma ^ 2 σ2 就会大一些,越接近均匀分布,算法就会遍历更多的区域,随着迭代次数的增加,慢慢地就会越来越接近最优区域,这时候方差应该要下降,使得极值点更为突出。也就是说,有可能的话,batch size应该要随着迭代次数而缓慢增加。**这就部分地解释了去年Google提出来的结果《学界 | 取代学习率衰减的新方法:谷歌大脑提出增加Batch Size》,不过batch size增加会大幅度增加计算成本,所以我们一般增加到一定量也就不去调整了。
当然,从图中可以看到,**当进入稳定下降区域时,每次迭代的步长 γ \gamma γ (学习率)就不应该超过“坑”的宽度,而 σ 2 \sigma ^ 2 σ2越小,坑也就越窄,这也表明学习率应该要随着迭代次数的增加而降低。**另外 γ \gamma γ 越大也部分地带来噪声,因此 σ 2 \sigma ^ 2 σ2降低事实上也就意味着我们要降低学习率。
所以分析结果就是:
条件允许情况下,在使用SGD时,开始使用小batch size和大学习率,然后让batch size慢慢增加,学习率慢慢减小。
至于增大、减少的策略,就要靠各位的炼丹水平了。