归并排序（Merge sort）

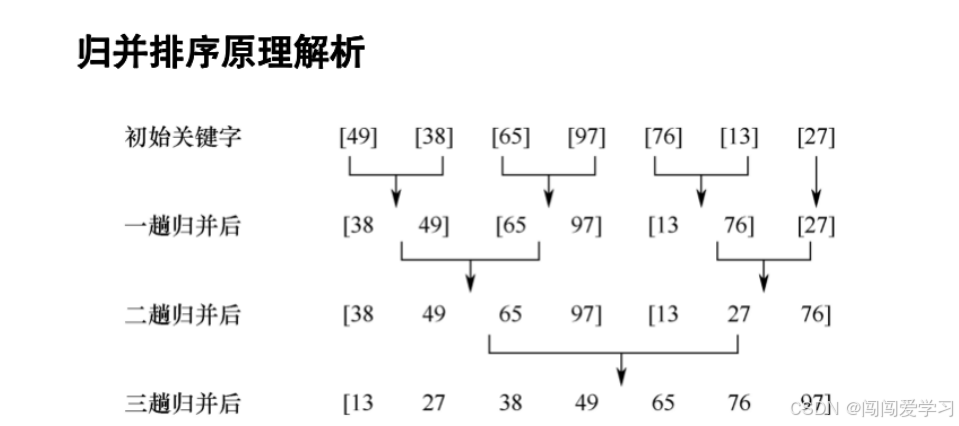
1、如上图所示

我们把每两个元素归为一组，进行小组内排序，然后再次把两个有序小组合并为一个有序小组，不断进行，最终合并为一个有序数组。

归并排序动画网址：https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

2、代码实战步骤：

归并排序是一种经典的分治算法，其核心思想是将一个大问题分解为多个小问题，分别解决这些小问题，然后将小问题的解合并起来得到大问题的解。

首先，最小下标值和最大下标值相加并除以 2，得到中间下标值mid，用MergeSort对low到mid 排序，然后用MergeSort对 mid+1到high排序，当数组的前半部分和后半部分都排好序后，使用Merge 函数.Merge函数的作用是合并两个有序数组。为了提高合并有序数组的效率，在Merge函数内定义了 B[N]。首先，我们通过循环把数组A中从low到high的元素全部复制到B中，这时游标i(遍历的变量称为游标)从low开始，游标j从mid+1开始，谁小就将谁先放人数组A对其游标加 1，并在每轮循环时对数组的计数游标k加1。

核心代码：

这段代码主要包含两个函数：Merge 函数和 MergeSort 函数。

Merge 函数的作用是将两个有序数组合并成一个有序数组;

代码解释：
- static ElemType B[N];：定义一个静态数组 B，用于临时存储数组 A 的元素。使用 static 关键字的目的是确保无论递归调用多少次 Merge 函数，都只有一个 B[N] 数组，避免重复创建数组，节省内存。
- for(k = low; k <= high; k++)：将数组 A 中从下标 low 到 high 的元素复制到数组 B 中。
- for(i = low, j = mid + 1, k = i; i <= mid && j <= high; k++)：合并两个有序子数组 B[low...mid] 和 B[mid+1...high]。比较 B[i] 和 B[j] 的大小，将较小的元素放入数组 A[k] 中，并将相应的指针后移。
- while(i <= mid) 和 while(j <= high)：处理剩余的元素。如果其中一个子数组已经遍历完，将另一个子数组中剩余的元素直接复制到数组 A 中。

MergeSort 函数则是利用分治思想对数组进行递归排序。
代码解释：
- if(low < high)：判断数组是否至少有两个元素。如果只有一个元素或者没有元素，则不需要排序。
- int mid = (low + high) / 2;：计算数组的中间位置。
- MergeSort(A, low, mid);：递归调用 MergeSort 函数，对数组的前一半进行排序。
- MergeSort(A, mid + 1, high);：递归调用 MergeSort 函数，对数组的后一半进行排序。
- Merge(A, low, mid, high);：调用 Merge 函数，将两个排序好的子数组合并成一个有序数组。

void Merge(ElemType A[],int low,int mid,int high)
{
    static ElemType B[N];//加static的目的是无论递归调用多少次，都只有一个B[N]
    int i,j,k;
    for(i=low;i<=high;i++)//把A[i]里面的元素都给B[i]
    {
        B[i]=A[i];
    }
    for(i=low,j=mid+1,k=i;i<=mid && j<=high;)//合并两个有序数组
    {
        if(B[i]<=B[j]){
            A[k]=B[i++];
            k++;
        }else{
            A[k]=B[j++];
            k++;
        }
    }
    //把某一个有序数组中剩余的元素放进来
    while(i<=mid)//前一半的有剩余的放入
    {
        A[k]=B[i++];//后一半的有剩余的放入
        k++;
    }
    while(j<=high)
    {
        A[k]=B[j++];
        k++;
    }
}

//归并排序不限制是两两归并，还是多个归并，但是考研一般都是考两两归并
void MergeSort(ElemType A[],int low,int high)
{
    if(low<high)
    {
        int mid=(low+high)/2;
        MergeSort(A,low,mid);//排序好前一半
        MergeSort(A,mid+1,high);//排序好后一半
        Merge(A,low,mid,high);//将两个排序好的数组合并
    }
}

完整代码：

#include <stdio.h>

#define N 7
typedef int ElemType;

//合并两个有序数组
void Merge(ElemType A[],int low,int mid,int high)
{
    static ElemType B[N];//加static的目的是无论递归调用多少次，都只有一个B[N]
    int i,j,k;
    for(i=low;i<=high;i++)//把A[i]里面的元素都给B[i]
    {
        B[i]=A[i];
    }
    for(i=low,j=mid+1,k=i;i<=mid && j<=high;)//合并两个有序数组
    {
        if(B[i]<=B[j]){
            A[k]=B[i++];
            k++;
        }else{
            A[k]=B[j++];
            k++;
        }
    }
    //把某一个有序数组中剩余的元素放进来
    while(i<=mid)//前一半的有剩余的放入
    {
        A[k]=B[i++];//后一半的有剩余的放入
        k++;
    }
    while(j<=high)
    {
        A[k]=B[j++];
        k++;
    }
}

//归并排序不限制是两两归并，还是多个归并，但是考研一般都是考两两归并
void MergeSort(ElemType A[],int low,int high)
{
    if(low<high)
    {
        int mid=(low+high)/2;
        MergeSort(A,low,mid);//排序好前一半
        MergeSort(A,mid+1,high);//排序好后一半
        Merge(A,low,mid,high);//将两个排序好的数组合并
    }
}

void print(int *a)
{
    for(int i=0;i<N;i++)
    {
        printf("%3d",a[i]);
    }
    printf("\n");
}

//归并排序
int main() {
    int A[7]={49,38,65,97,76,13,27};
    MergeSort(A,0,6);
    print(A);
    return 0;
}

3、时间复杂度与空间复杂度

MergeSort 函数的递归次数是log2n,Merge 函数的循环了n次，因此时间复杂度是 O(nlog2n).归并排序最好、最坏、平均时间复杂度都是 O(nlog2n).归并排序的空间复杂度是 O(n)，因为使用了数组B，它的大小与A一样，占用n个元素的空间。