一.解法思路
买卖股票的最佳时机系列是十分经典的多状态DP问题。分析这种多状态DP问题我们可以借助状态机的思想。我们可以根据问题分析出这个问题有几个状态,每个状态之间是怎么转化的。通过转化的方式我们可以写出状态转移方程。状态转移方程这个很好理解,就是状态要转移时要付出的代价(进行的转化)。
当然,这么看还是有点抽象,还是直接看题理解。
二.买卖股票的最佳时机 II
题目链接:122. 买卖股票的最佳时机 II
1.题目分析
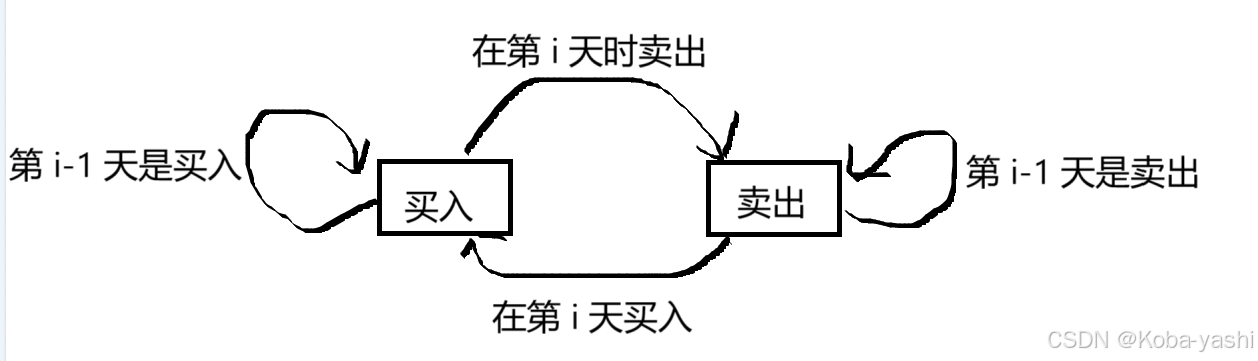
题目还是很好理解的,就是一个买卖的问题。我们不难发现,买卖股票的时候有两种状态:买入和卖出,这就是我们上面说的“状态”。有了状态,我们就要状态之间是怎么转换的。这里我们可以通过画一个图来理解。规定这里的状态指的是在第 i 天结束时的状态。
如果在第 i 天结束的时候是买入的状态,那么在第 i-1 天会是什么状态?无疑也是两种,一种是买入,也就是在第 i 天的时候什么也没干;一种是卖出,那么也就表名我们在第 i 天的时候买入了股票。
分析第 i 天是卖出状态的时候也是同理的。第 i-1 天的可能是卖出或是买入。
明白了状态是怎么转化的,下面就要写状态转移方程了。在写状态转移方程前,我们先要规定好变量。
int[][] dp=new int[n][2];解释:dp数组指的是第 i 天解释时,卖出或买入状态的最大利润。这是一个二维数组,当是dp[i][0]时,这就是在第i天结束时,状态是买入状态的最大值。dp[i][1]就是在第 i 天结束时,状态是卖出状态时的最大值。
好了,明确了dp是什么就可以写状态转移方程了。
买入状态可以怎么转化来,1.第 i-1 天的买入;2.第 i 天买入了股票。
所以我们就可以写:
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);题目要求的是最大值,所以我们这里进行了取最大值的操作。dp[i-1][0]表示在第 i-1 天结束时状态是买入的最大利润,dp[i-1][1]表示在第 i-1 天结束时状态是卖出的最大利润。这里减prices[i]是因为我们花钱买了股票,要用利润中扣。
卖出状态也是同理:
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);有了这两个状态转移方程,题目就接出来了。
最后补充一个细节问题:初始化。注意我们上面的式子中都有 i-1 。如果i=0时,就会报错。因此我们要对dp[0][0]和dp[0][1]进行初始化。
i=0时,表示整个数组就有prices[0]这一个变量,我们只有买和不买两种可能。如果买入,dp[0][0]=-prices[0](因为是买入,要扣钱,dp表示的是利润)。如果不买,那就属于卖出的状态,dp[0][1]=0。
2.代码
class Solution {
public int maxProfit(int[] prices) {
int n=prices.length;
int[][] dp=new int[n][2];
dp[0][0]=-prices[0];
for(int i=1;i<n;i++){
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);
}
return Math.max(dp[n-1][0],dp[n-1][1]);
}
}三.买卖股票的最佳时机 III
1.题目分析
题目链接:买卖股票的最佳时机 III
大体内容与上一个题相似,这里引入了一个新的限制,就是只能进行两笔交易。
这里的状态还是两种:买入和卖出。但是在买入和卖出的基础上要加上进行的交易的数量,即在第 i 天结束时进行了多少次交易。
交易次数最多可以有两次,也就是说我们在第 i 天可以有 0、1、2笔交易。
对于这种问题,我们要使用三维数组去存利润:
int[][][] dp=new int[n][2][3];前面的n和2跟上面的一样就不解释了,而这个3是指交易次数的三种可能。同时我们规定,在进行卖出股票的操作时,才算完成了一次交易。如果只是买入没有卖出,不算一次交易。
这个图还是没有变的,还是这么转化的,但是状态转移方程要变。
如果第 i 天是买入操作,那么其可能是第 i-1 天是买入的状态,同时,由于一直是买入的状态,因此原来是多少笔交易,现在还是多少;第 i-1 天是卖出的状态,我们已经规定好了,买入不算交易次数,因此交易次数还是不变的。(j表示进行了几次交易)
dp[i][0][j]=Math.max(dp[i-1][0][j],dp[i-1][1][j]-prices[i]);如果第 i 天是买入操作,第 i-1 天可能是卖出,同时,由于一直是卖出的状态,交易次数不变;但是第 i-1 天是买入的状态时,就是注意了,这说明我们进行了卖出操作,交易次数要加1了。
dp[i][1][j]=Math.max(dp[i-1][1][j],dp[i-1][0][j-1]+prices[i]);上面代码有一个问题,当j=0时,会出现错误,因此我们要处理以下这种特殊情况:
dp[i][1][j]=dp[i-1][1][j];
if(j-1>=0){
dp[i][1][j]=Math.max(dp[i][1][j],dp[i-1][0][j-1]+prices[i]);
}下面我们要处理一下初始化问题,当i=0时,我们不可能进行了1笔或2笔交易,只能进行0笔交易。同时,我们也不能卖出股票。我们这里取的都是最大值,为了不干扰交易,我们要将那些无关的位置都赋值一个很小的数。
那些位置是无关的?i=0时,j=1,2(都是不可能的情况)。dp[0][0][0]依旧是减掉prices[0]。
这个题还有一个问题就是最后取最大值的问题。最后的最大值可能取的是交易次数是0,1,2的时候。这些都有可能是答案。
2.代码
class Solution {
public int maxProfit(int[] prices) {
int n=prices.length;
int[][][] dp=new int[n][2][3];
for(int i=1;i<3;i++){
dp[0][0][i]=-0x3f3f3f3f;
dp[0][1][i]=-0x3f3f3f3f;
}
dp[0][0][0]-=prices[0];
for(int i=1;i<n;i++){
for(int j=0;j<3;j++){
dp[i][0][j]=Math.max(dp[i-1][0][j],dp[i-1][1][j]-prices[i]);
dp[i][1][j]=dp[i-1][1][j];
if(j-1>=0){
dp[i][1][j]=Math.max(dp[i][1][j],dp[i-1][0][j-1]+prices[i]);
}
}
}
int ans=0;
for(int i=0;i<3;i++){
ans=Math.max(ans,Math.max(dp[n-1][0][i],dp[n-1][1][i]));
}
return ans;
}
}四.买卖股票的最佳时机 IV
1.题目分析
题目链接:买卖股票的最佳时机 IV
这个题跟上的没有区别,分析思路是一样的,只不过把2换成了k,直接上代码。
2.代码
class Solution {
public int maxProfit(int k, int[] prices) {
int n=prices.length;
int[][][] dp=new int[n][2][k+1];
for(int i=1;i<k+1;i++){
dp[0][0][i]=-0x3f3f3f3f;
dp[0][1][i]=-0x3f3f3f3f;
}
dp[0][0][0]-=prices[0];
for(int i=1;i<n;i++){
for(int j=0;j<k+1;j++){
dp[i][0][j]=Math.max(dp[i-1][0][j],dp[i-1][1][j]-prices[i]);
dp[i][1][j]=dp[i-1][1][j];
if(j-1>=0){
dp[i][1][j]=Math.max(dp[i][1][j],dp[i-1][0][j-1]+prices[i]);
}
}
}
int ans=0;
for(int i=0;i<k+1;i++){
ans=Math.max(ans,Math.max(dp[n-1][0][i],dp[n-1][1][i]));
}
return ans;
}
}五.买卖股票的最佳时机含手续费
1.题目分析
题目链接:714. 买卖股票的最佳时机含手续费
这个题属于买卖股票的最佳时机 II 的变种,即在 II 的基础上添加了手续费这个元素。万变不离其宗,其实没什么区别。
状态还是:买入和卖出。只不过我们要在卖出的时候减掉手续费。
2.代码
class Solution {
public int maxProfit(int[] prices, int fee) {
int n=prices.length;
int[][] dp=new int[n][2];
dp[0][0]-=prices[0];
for(int i=1;i<n;i++){
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]+prices[i]-fee);
}
return Math.max(dp[n-1][0],dp[n-1][1]);
}
}六.买卖股票的最佳时机含冷冻期
1.题目分析
题目链接:309. 买卖股票的最佳时机含冷冻期
这个也是买卖股票的最佳时机 II 的变种,不过这个就稍微难一些了。这个出现了三个状态:买入,卖出,冷冻期。冷冻期不能像前面的一样,归入到买入或卖出中。在冷冻期内我们什么也干不了。
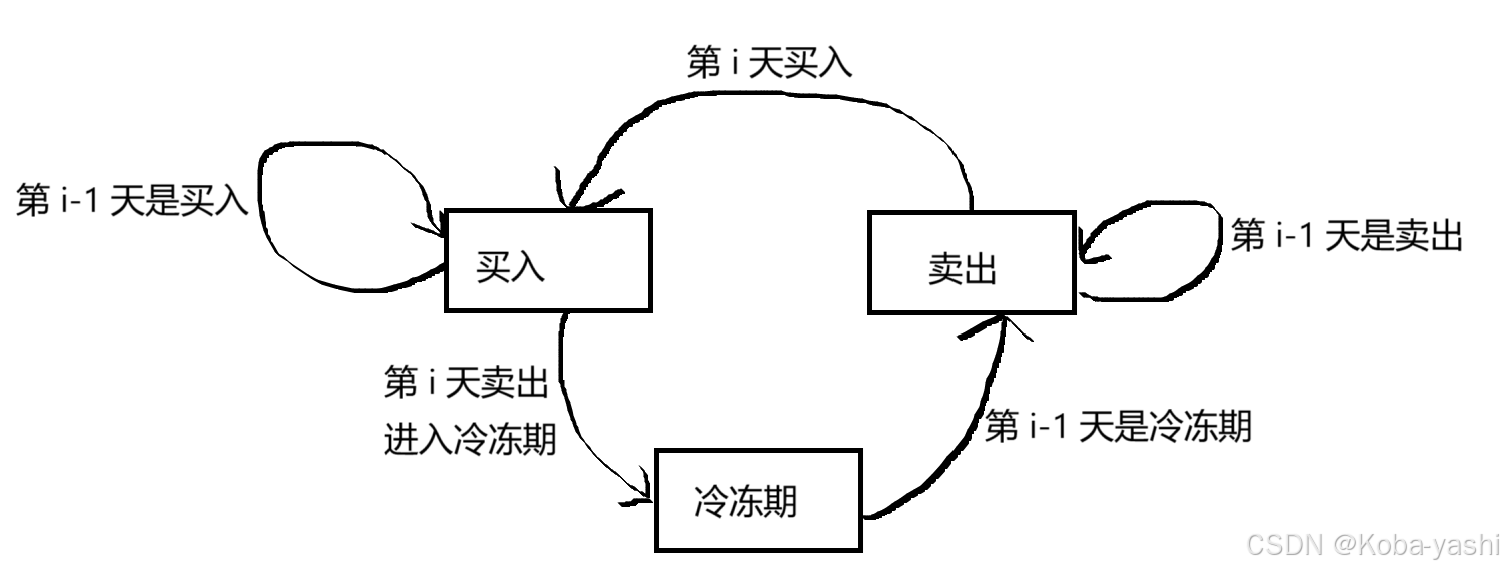
我们还是通过画图来分析问题:
这个图看起来比上面复杂一些。但我们还是一样的分析方法。这里有个技巧,我们状态太多了不好去分析到底两者直接能不能相互转化,我们可以给每个状态之间都加上连线,一条一条验证可不可能,将不可能的去掉即可,这样我们就可以得到不漏的完整关系。
有了图,我们就可以写状态转移方程了。(注意,这里的第 i 天的状态依旧是第 i 天结束时的状态)
当第 i 天是买入时,第 i-1 天可以时买入状态,可以是卖出状态。
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);当第 i 天是冷冻期时,第 i-1 天只能是买入状态,我们在第 i 天卖出了股票。
dp[i][2]=dp[i-1][0]+prices[i];当第 i 天是卖出状态时,第 i-1 天可能是冷冻期,也可能是卖出。但不可能是买入,因为卖掉股票要进入冷冻期。
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][2]);2.代码
class Solution {
public int maxProfit(int[] prices) {
int n=prices.length;
int[][] dp=new int[n][3];
dp[0][0]-=prices[0];
for(int i=1;i<n;i++){
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][2]);
dp[i][2]=dp[i-1][0]+prices[i];
}
return Math.max(dp[n-1][0],Math.max(dp[n-1][1],dp[n-1][2]));
}
}七.总结
上面介绍了买卖股票的系列问题,他们都有共性,都是多状态DP。我们在做多状态DP时可以像上面一样,先找出状态,在画图找出状态之间是怎么转化的,最后写状态转移方程。买卖股票问题还是属于简单的问题,如果想要更近一步的话还要做更多的题。这里只是提供了一个做多状态DP问题时的思路。