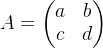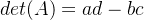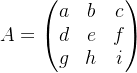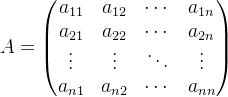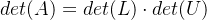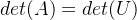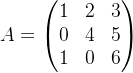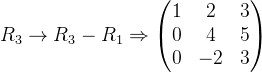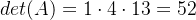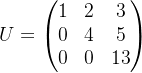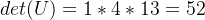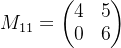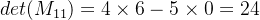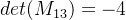行列式（Determinant）是线性代数中一个重要的概念，用来描述方阵的一些性质，尤其是与矩阵的可逆性、特征值等有关。下面是几种常见的计算行列式的方法：

1. 2x2矩阵的行列式

对于一个2x2矩阵：

行列式计算公式是：

2. 3x3矩阵的行列式

对于一个3x3矩阵：

行列式的计算公式是：

具体步骤：

• 计算每个2x2子矩阵的行列式。
• 按照加减法则将它们加权求和。

3. n x n矩阵的行列式（展开法）

对于n x n的矩阵，可以使用按行或按列展开的方法计算行列式。

以按第一行展开为例，若有矩阵：

行列式的展开式为：

其中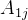，是去掉第1行第j列后的子矩阵，行列式的计算递归进行。

4. 使用初等变换计算行列式

可以通过对矩阵进行初等行变换来简化行列式的计算：

• 交换两行：行列式符号改变，即乘以-1。
• 将一行乘以一个常数k：行列式乘以k。
• 将一行加到另一行：行列式不变。

如果通过初等变换将矩阵化为上三角矩阵或下三角矩阵，行列式等于对角线元素的乘积。

5. 利用LU分解计算行列式

将矩阵A分解为LU形式（上三角矩阵L和下三角矩阵U），则行列式满足：

因为L是单位下三角矩阵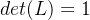，，所以：

而上三角矩阵U的行列式等于其对角线元素的乘积。

6. Cofactor展开法（伴随矩阵法）

伴随矩阵是通过计算矩阵的每个元素的余子式得到的。

通过余子式和伴随矩阵的关系，也可以计算行列式，特别适用于计算伴随矩阵等问题。

例题

假设我们有如下矩阵：

方法1：直接按行列式展开（使用3x3矩阵的展开公式）

det(A)=1×(4×6−5×0)−2×(0×6−5×1)+3×(0×0−4×1)=52

方法2：使用初等行变换简化矩阵

• 用第3行减去第1行，使得第3行的第一列为0：

• 用第3行加上第2行的两倍，使得第3行第二列为0：

• 现在，我们得到了上三角矩阵：

方法3：LU分解

• 矩阵A的LU分解形式为：A=LU，其中L是下三角矩阵，U是上三角矩阵。
• 通过高斯消元法，可以得到：

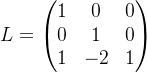
• 行列式是L和U的行列式的乘积。因为L的行列式是1（L是单位下三角矩阵），U的行列式是其对角线元素的乘积，即：

方法4：Cofactor展开法（伴随矩阵法）

步骤1：计算余子式（Minor）

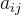
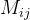
对于矩阵 A中的每个元素 ，我们首先计算其余子式 ，即删除第i行第j列后，剩下的子矩阵的行列式。

去掉第一行第一列，得到的子矩阵：

行列式为：

依次得到，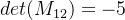

步骤2：计算代数余子式（Cofactor）

代数余子式是余子式的值乘以 ，其中 i和 j 是元素 的行和列索引。

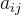
步骤3：计算行列式

根据代数余子式展开行列式：