算法复习
知识点
- 多项式时间复杂度是指在多项式阶内(例如,O(n^2), O(n^3))增长的算法。
- AOE网中的关键路径 ,就是完成整个网络所需的最短时间,亦最长路径 ,AOE网中,往往有若干项活动可以平行的进行,因此,从开始顶点到最后一个顶点的最长路径称为关键路径 。
- NP完全问题
-
最小代价生成树问题的目标是找到一个生成树,使得这棵树上所有边的权重之和最小。两个常用的算法来解决最小代价生成树问题是Kruskal算法和Prim算法(这两种都是贪心算法)。
- Kruskal算法: 通过不断选择图中权重最小的边,并确保不形成环,逐步构建最小代价生成树。
- Prim算法: 从一个初始顶点开始,选择连接当前树和其他顶点的边中权重最小的边,然后将新顶点加入树中,重复这个过程,直到生成树包含了图中所有的顶点。
-
分治法的基本思想就是将原问题分解成若干个规模较小且结构与原问题相似的子问题,然后递归地解决这些子问题,最后再合并子问题的解得到原问题的解。两路合并排序完全符合这一思想。
-
贪心算法通常适用于具有以下特征的组合优化问题: - 最优子结构性质:一个问题的最优解包含其子问题的最优解; - 贪心选择性质:可以通过局部最优选择来达到全局最优结果,并且对于每个子问题都可以做出这样的选择;
-
-
-
-
MST(最小代价生成树)
-
-
-
回溯法 蒙特卡罗方法
计算递推式
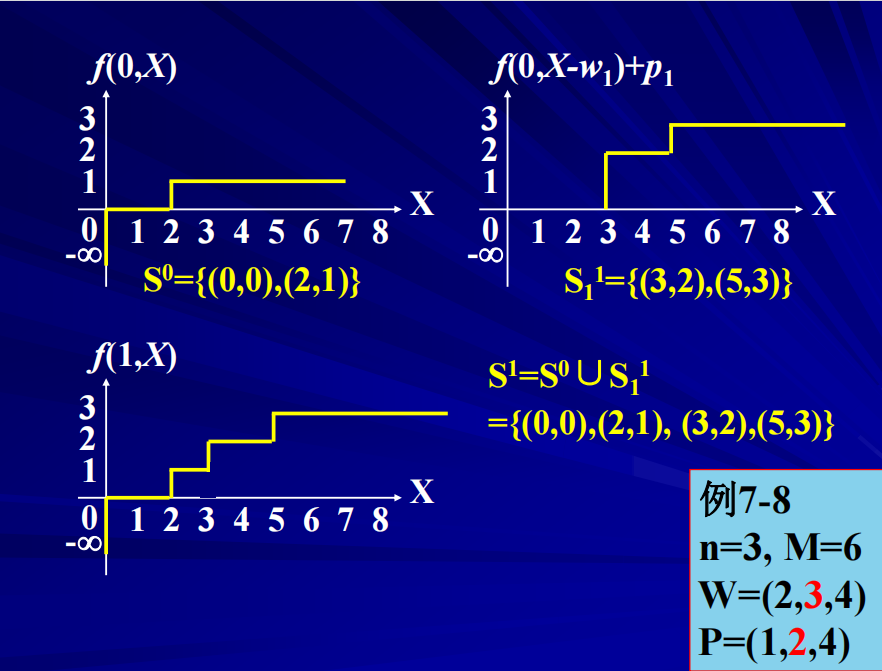
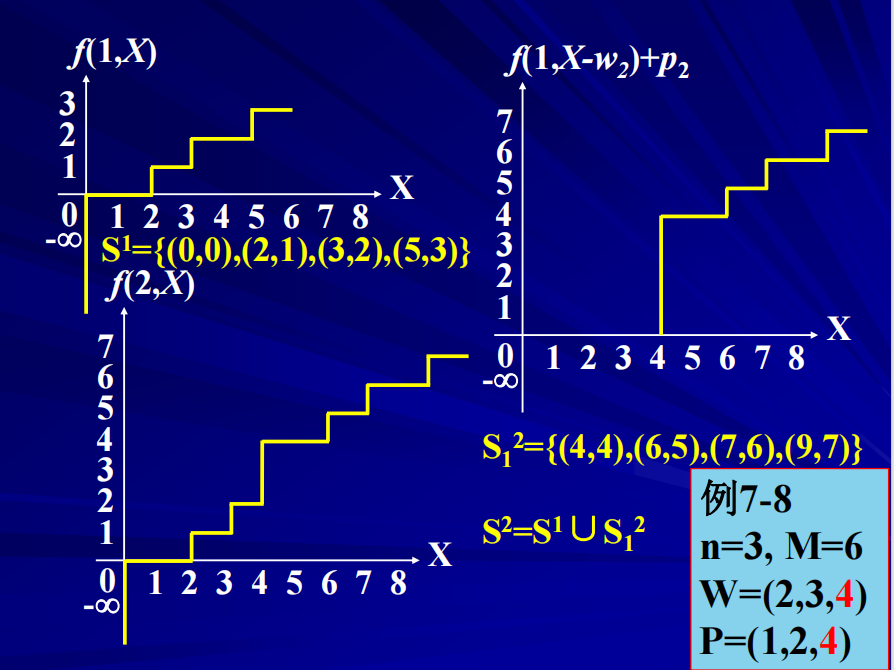
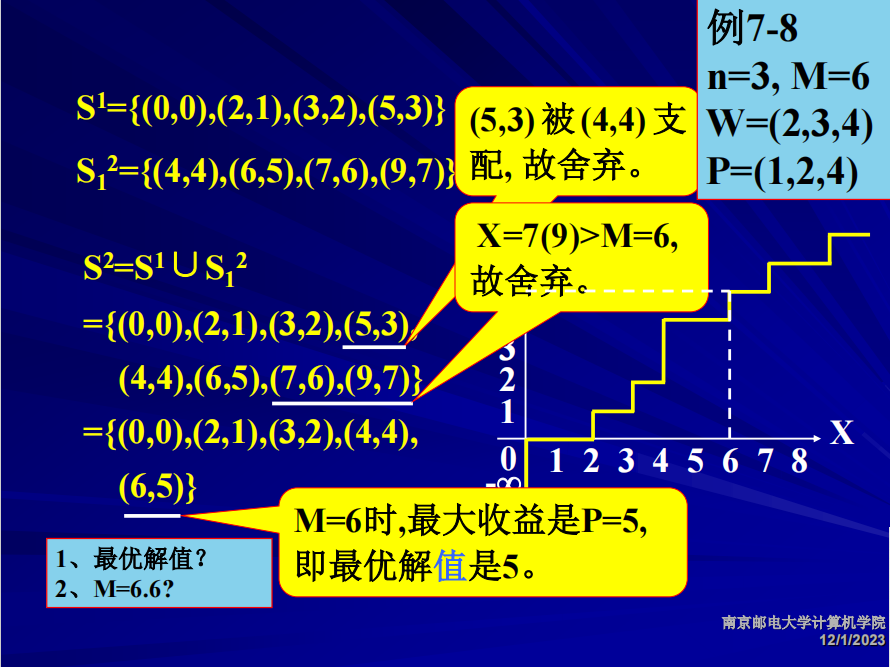
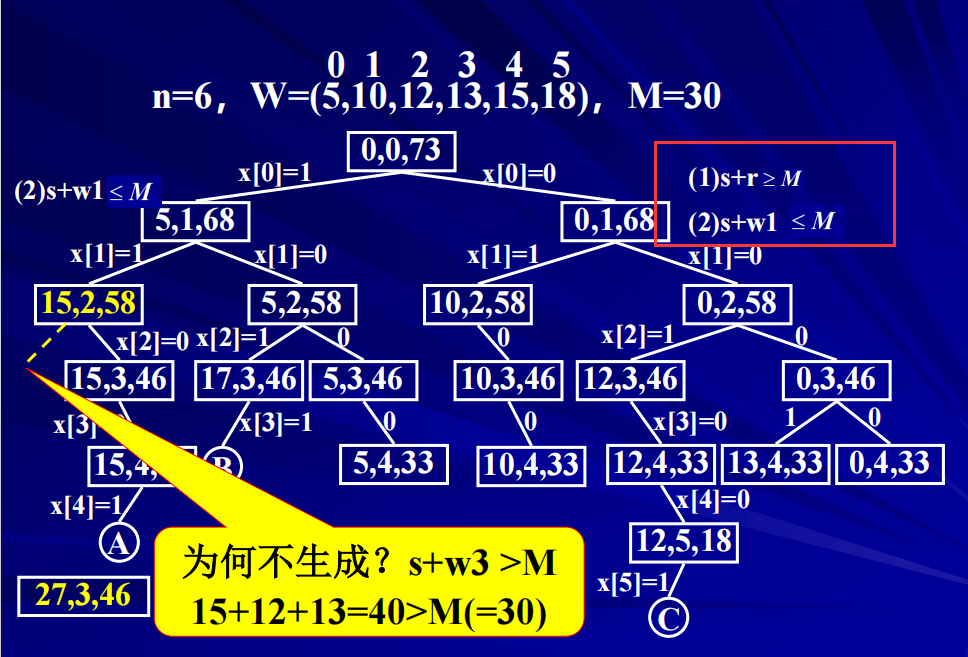
背包问题
01背包问题
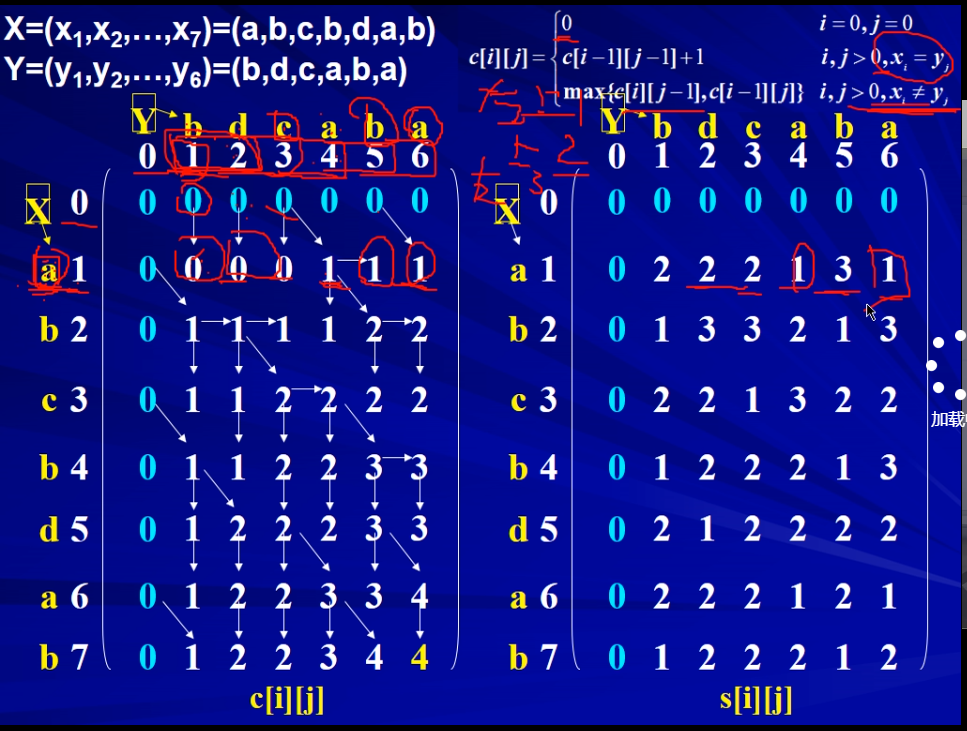
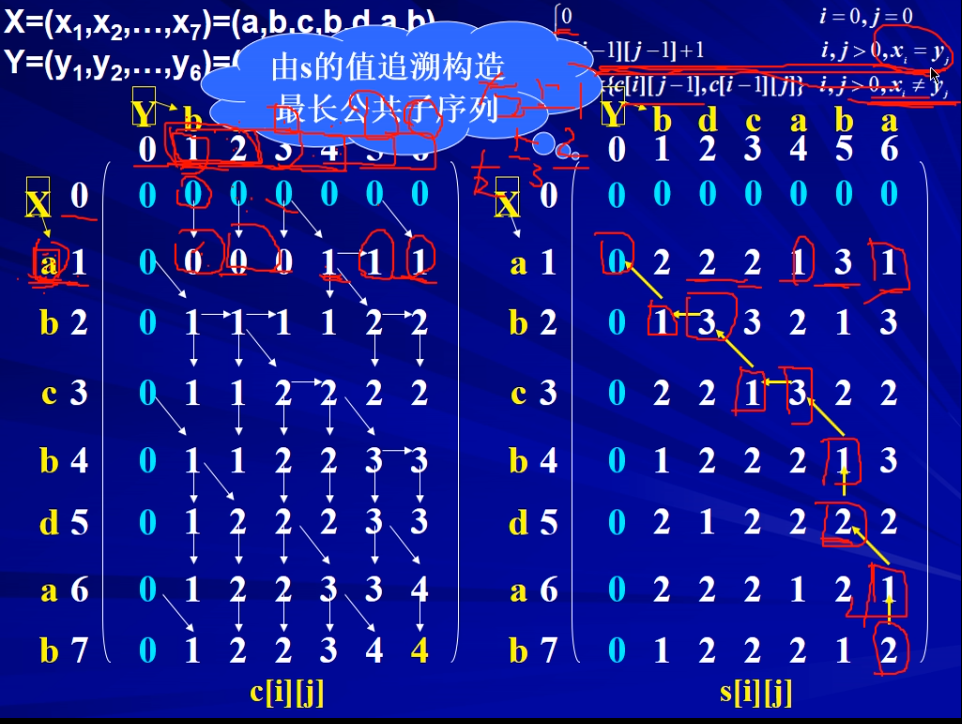
最长公共子序列
子集和数算法
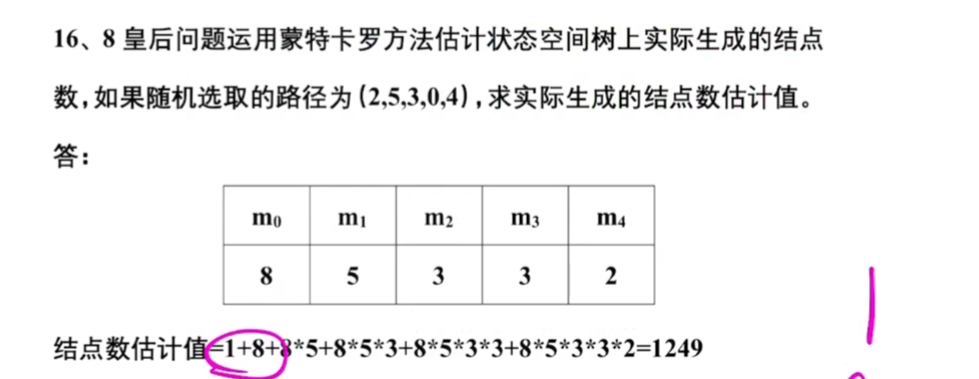
八皇后(回溯)
分支限界法
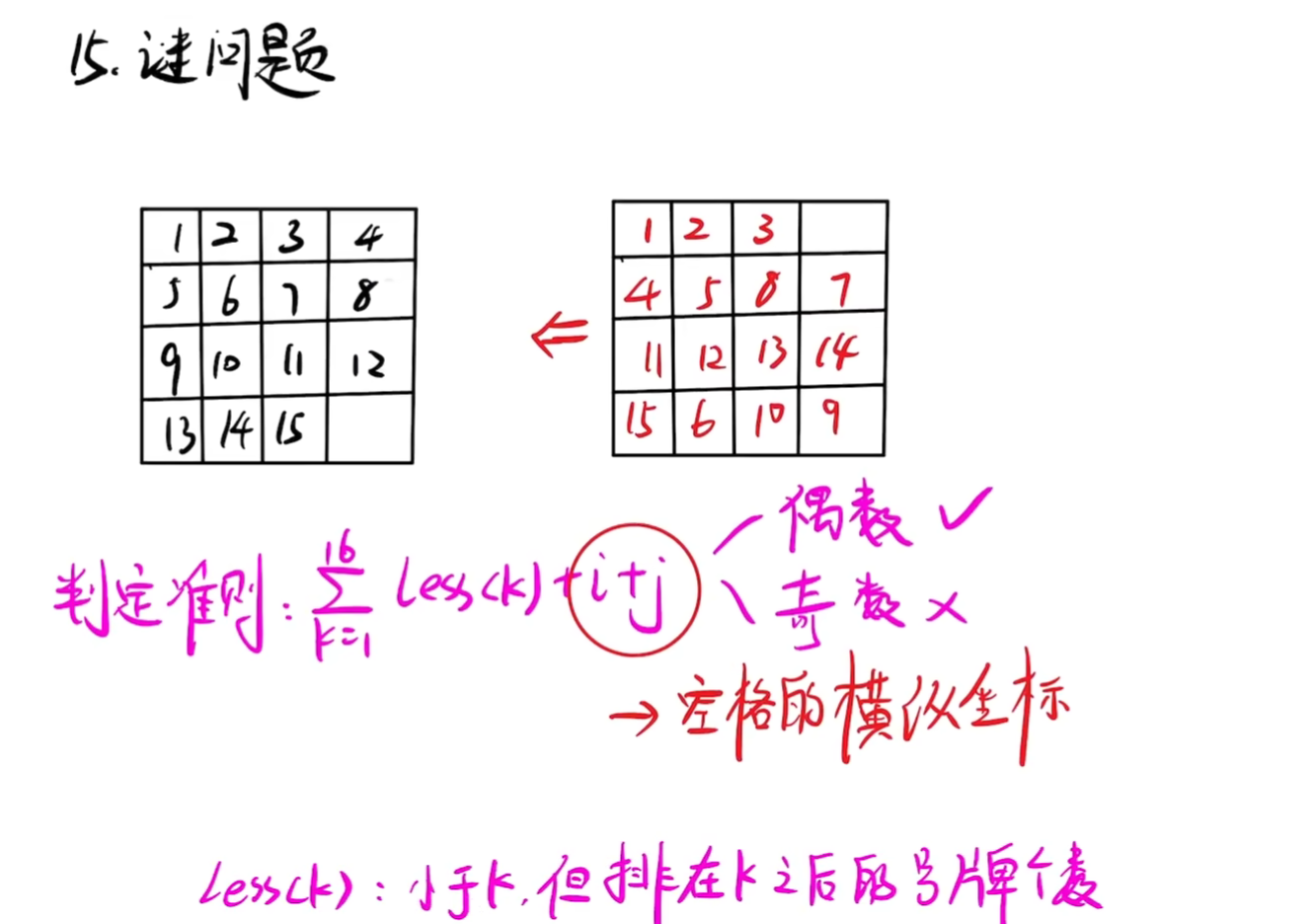
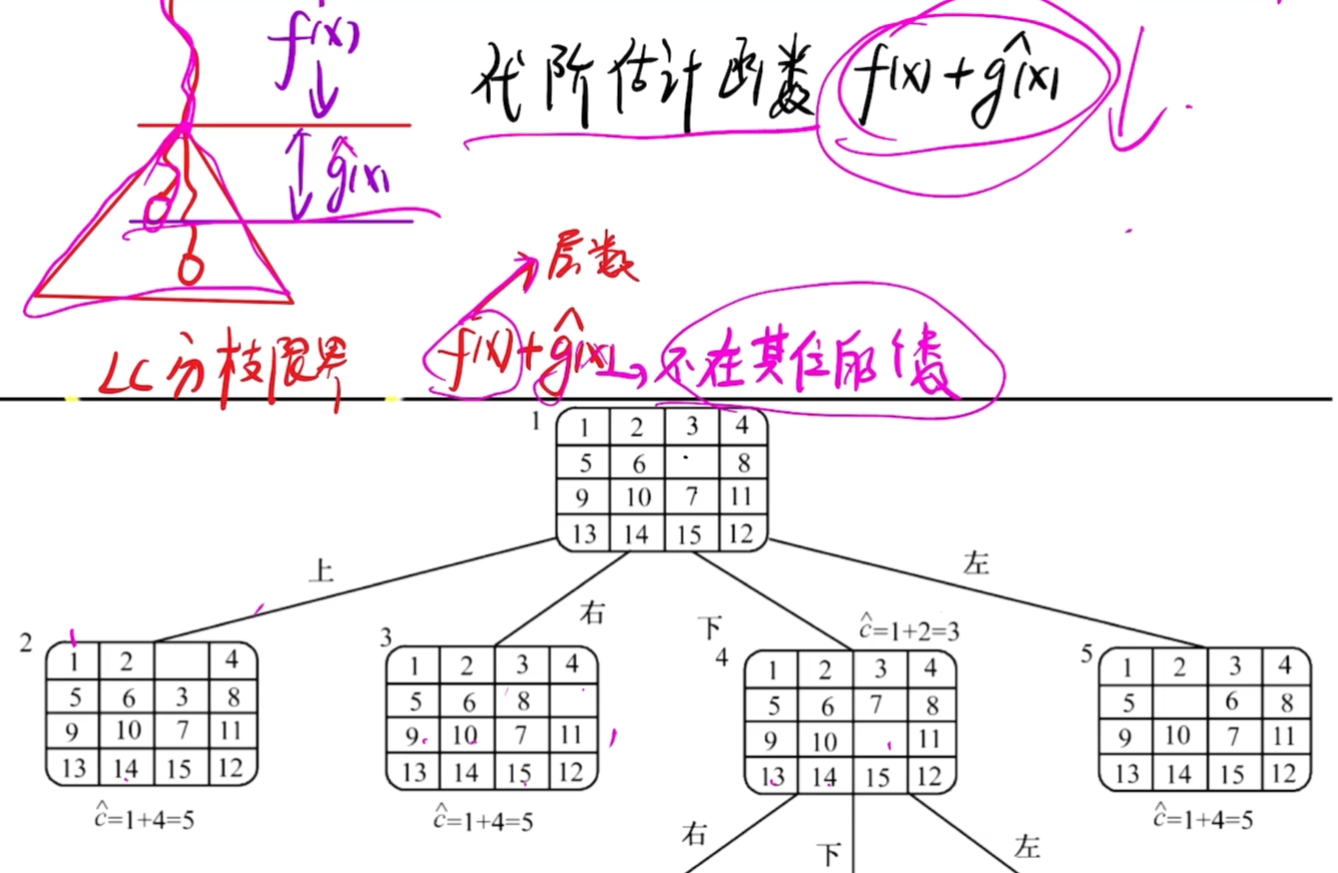
15迷问题
- LC分支限界快速求解
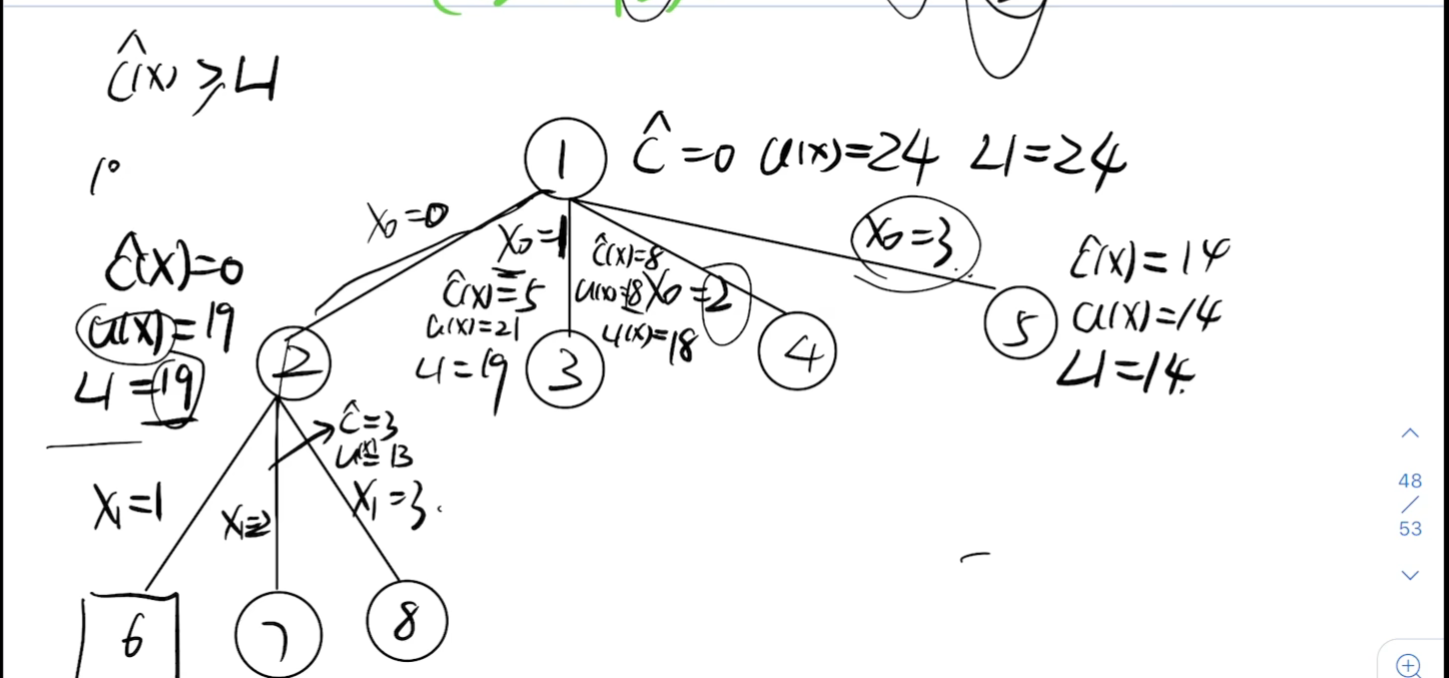
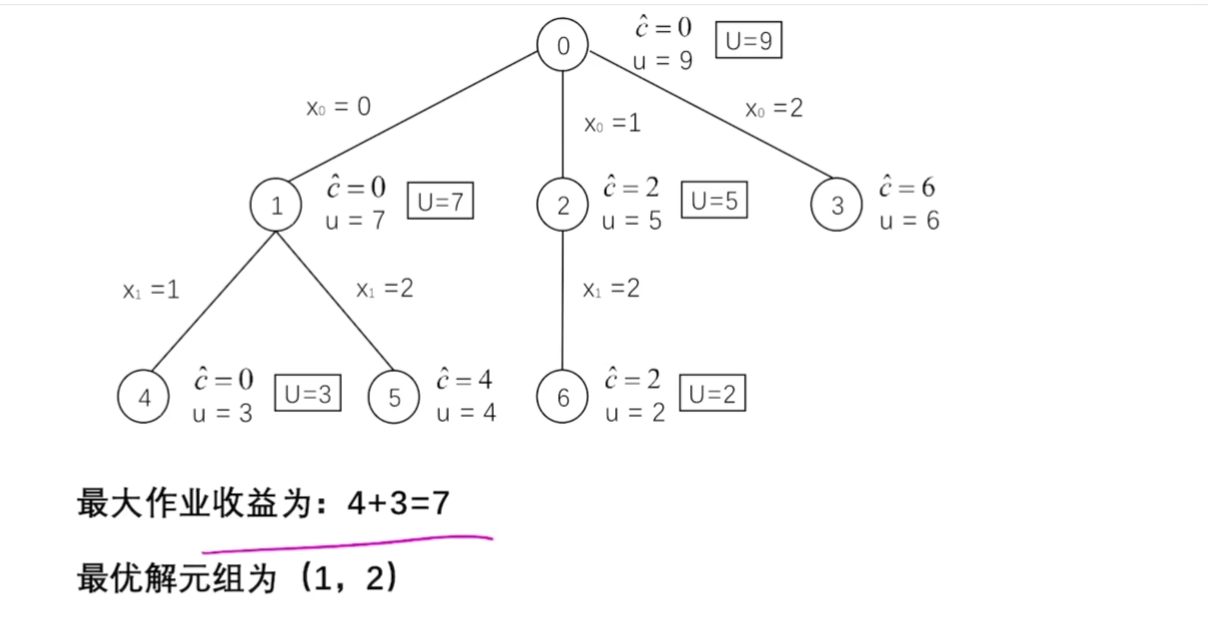
带时限的作业排序
- 分支限界法求解最优解问题
- 例题