介绍
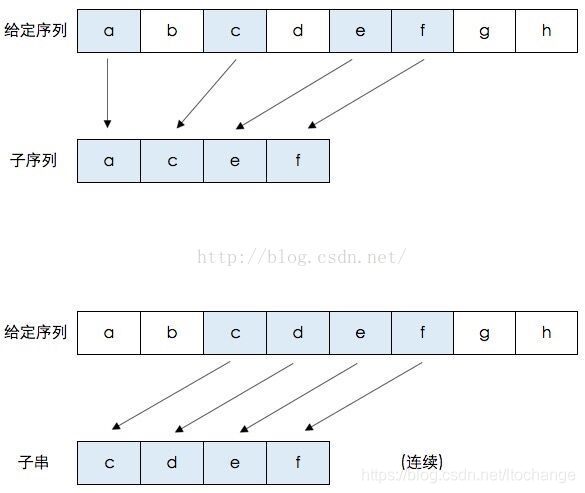
子序列和子串的意思不一样,如下图所示,子序列不要求连续,只需要在给定序列中出现过,并且相对顺序一致。而子串需要连续。
图片来自动态规划 最长公共子序列 过程图解
最长公共子序列(LCS):
同时出现在两个字符串中的最长子序列
实现
思想和求解两个字符串之间的编辑距离差不多,使用动态规划的方法,递推公式如下:
d p [ i , j ] dp[i, j] dp[i,j]表示字符串 x [ : i ] x[:i] x[:i]与字符串 y [ : j ] y[:j] y[:j]之间的最长公共子序列长度
d p [ i , j ] = { 0 若 i = 0 或 j = 0 d p [ i − 1 , j − 1 ] + 1 若 i , j ≥ 0 , x i − 1 = y j − 1 max { d p [ i , j − 1 ] , d p [ i − 1 , j ] } 若 i , j ≥ 0 , x i − 1 ≠ y j − 1 dp[i, j]= \begin{cases}0 & \text { 若 } i=0 \text { 或 } j=0 \\ dp[i-1, j-1]+1 & \text { 若 } i, j\geq0, x_{i-1}=y_{j-1} \\ \max \{dp[i, j-1], dp[i-1, j]\} & \text { 若 } i, j\geq0, x_{i-1} \neq y_{j-1}\end{cases} dp[i,j]=⎩⎪⎨⎪⎧0dp[i−1,j−1]+1max{dp[i,j−1],dp[i−1,j]} 若 i=0 或 j=0 若 i,j≥0,xi−1=yj−1 若 i,j≥0,xi−1=yj−1
代码如下:
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
m = len(text1)
n = len(text2)
res = ""
# 记录最长的公共子序列
if m * n == 0:
return 0
dp = [[0] * (n + 1) for _ in range(m + 1)]
# dp[i][j]表示text1[:i]与text[:j]的最长公共子序列长度
for i in range(1, m + 1):
for j in range(1, n + 1):
if text1[i - 1] == text2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
res += text1[i - 1]
else:
dp[i][j] = max([dp[i - 1][j], dp[i][j - 1]])
print(res)
return dp[m][n]
时间复杂度:O(mn)
空间复杂度:O(mn)
测试:
text1 = "abcde"
text2 = "ace"
obj = Solution()
res = obj.longestCommonSubsequence(text1, text2)
print(res)
# 3,最长公共子序列是ace
# ace 可以在计算dp的过程中保存得到
上面的代码中,dp只需要用到上一行i-1的结果,因此可以进行空间优化,只保存上一行以及当前行的结果。
class Solution:
def longestCommonSubsequence_1(self, text1: str, text2: str) -> int:
m = len(text1)
n = len(text2)
res = ""
# 记录最长的公共子序列
if m * n == 0:
return 0
dp = [[0] * (n + 1) for _ in range(2)]
# dp[i][j]表示text1[:i]与text[:j]的最长公共子序列长度
pre = 0
cur = 1
# pre存储上一行的结果,cur存储当前行结构
# pre和cur在内存中的位置一会是第0行,一会是第1行
for i in range(1, m + 1):
for j in range(1, n + 1):
if text1[i - 1] == text2[j - 1]:
dp[cur][j] = dp[pre][j - 1] + 1
res += text1[i - 1]
else:
dp[cur][j] = max([dp[pre][j], dp[cur][j - 1]])
tmp = pre
pre = cur
cur = tmp
print(res)
return dp[pre][n]
时间复杂度:O(mn)
空间复杂度:O(2n)