🧡🧡实验内容🧡🧡

编写 BP 神经网络分类, 实现对 MNIST 数据集分类的操作。

🧡🧡代码🧡🧡

需要配置torch。由于是小demo。为了提高效率，我采用的是google的colab进行实验编码，省去配环境的烦恼。

import os
import numpy as np
import torch
import matplotlib.pyplot as plt
from time import time
from torchvision import datasets, transforms
from torch import nn, optim

#@title 加载
transform = transforms.Compose([
                transforms.ToTensor(), # 转为张量，同时如果是图片（uint8）类型，会自动进行归一化到（0，1）
                transforms.Normalize( (0.5, ) , (0.5, ) ) # 转为std=0.5、mean=0.5的分布, 灰色图像，通道只有一个  将值域(0,1)再次转为(-1,1)
                ])
train_set = datasets.MNIST('train_set', # 下载到该文件夹下
              download=not os.path.exists('train_set'), # 是否下载，如果下载过，则不重复下载
              train=True, # 是否为训练集
              transform=transform # 要对图片做的transform
              )
test_set = datasets.MNIST('test_set',
              download=not os.path.exists('test_set'),
              train=False,
              transform=transform
              )
test_set
# train_set[0][0]
train_loader = torch.utils.data.DataLoader(train_set, batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=64, shuffle=True)

dataiter = iter(train_loader)
images, labels = next(iter(dataiter))
print(images.shape)
print(labels.shape)


#@title Bp net
class BP_Net(nn.Module):
    def __init__(self):
        super().__init__()
        """
        定义第一个线性层，
        输入为图片（28x28），
        输出为第一个隐层的输入，大小为128。
        """
        self.linear1 = nn.Linear(28 * 28, 128)
        self.relu1 = nn.ReLU() # 在第一个隐层使用ReLU激活函数
        """
        定义第二个线性层，
        输入是第一个隐层的输出，
        输出为第二个隐层的输入，大小为64。
        """
        self.linear2 = nn.Linear(128, 64)
        self.relu2 = nn.ReLU() # 在第二个隐层使用ReLU激活函数
        """
        定义第三个线性层，
        输入是第二个隐层的输出，
        输出为输出层，大小为10
        """
        self.linear3 = nn.Linear(64, 10)
        self.softmax = nn.LogSoftmax(dim=1) # 最终的输出经过softmax进行归一化

    def forward(self, x):
        """
        定义神经网络的前向传播
        x: 输入的图片数据, shape为(64, 1, 28, 28)
        """
        x = x.view(x.shape[0], -1) # 首先将x的shape转为(64, 784)

        # 进行前向传播
        x = self.linear1(x)
        x = self.relu1(x)
        x = self.linear2(x)
        x = self.relu2(x)
        x = self.linear3(x)
        x = self.softmax(x)

        return x
model = BP_Net()
criterion = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(), lr=0.003, momentum=0.9)

#@title 评估
from sklearn.metrics import confusion_matrix, roc_auc_score, roc_curve
model.eval() # 将模型设置为评估模式

correct_count, all_count = 0, 0
predictions = [] # 预测结果列表
true_labels = [] # 真实标签列表

for images,labels in test_loader: # 从test_loader中一批一批加载图片
    for i in range(len(labels)):
        logps = model(images[i])  # 进行前向传播，获取预测值
        probab = list(logps.detach().numpy()[0]) # 将预测结果转为概率列表。[0]是取第一张照片的10个数字的概率列表（因为一次只预测一张照片）
        pred_label = probab.index(max(probab)) # 取最大的index作为预测结果
        true_label = labels.numpy()[i]
        if(true_label == pred_label): # 判断是否预测正确
            correct_count += 1
        all_count += 1
        predictions.append(pred_label)
        true_labels.append(true_label)

# 准确率
print("Number Of Images Tested =", all_count)
print("Model Accuracy =", (correct_count/all_count))

# 混淆矩阵
def plot_confusion_matrix(cm, classes):
    plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
    plt.title("Confusion Matrix")
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes)
    plt.yticks(tick_marks, classes)
    thresh = cm.max() / 2
    for i in range(cm.shape[0]):
        for j in range(cm.shape[1]):
            plt.text(j, i, format(cm[i, j], 'd'), ha="center", va="center",
                     color="white" if cm[i, j] > thresh else "black")
    plt.ylabel('True Label')
    plt.xlabel('Predicted Label')
    plt.tight_layout()
    plt.show()

cm = confusion_matrix(true_labels, predictions)
classes = [str(i) for i in range(10)]
plot_confusion_matrix(cm, classes)

#@title 验证
model.train() # 切回训练模式

## 验证本地图片
import cv2
from PIL import Image
for num in range(0,10):
    img = cv2.imread('./myImg/{}.jpg'.format(num), 0)  # 以灰度图的方式读取要预测的图片
    img = cv2.resize(img, (28, 28))
    height, width = img.shape
    dst = np.zeros((height, width), np.uint8)
    for i in range(height):
        for j in range(width):
            dst[i, j] = 255 - img[i, j]
    dst= dst / 255.0 #归一化
    dst = (dst - 0.5) / 0.5  # 标准化到[-1, 1]
    img = dst
    # print(img)
    img = np.array(img).astype(np.float32)
    img = np.expand_dims(img, 0)  # 扩展后，为[1，28，28]
    img = np.expand_dims(img, 0)  # 扩展后，为[1，1，28，28]
    img = torch.from_numpy(img)
    # print(img.shape)
    with torch.no_grad():
        output=model(img)
    # print(output.data)
    print(output.data.max(1)[1])

🧡🧡分析结果🧡🧡

数据预处理：

• 加载数据集：
  加载torch自带的minst数据集
• 转换数据：
  先转为tensor变量（相当于直接除255归一化到值域为(0,1)）
  
  然后根据std=0.5，mean=0.5，再将值域标准化到（-1，1）
  

设置基本参数：

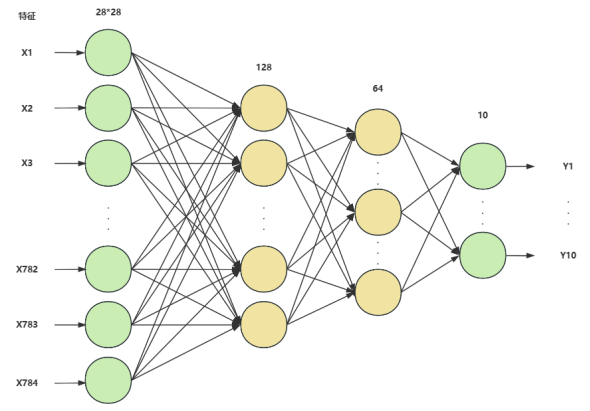
构建BP神经网络：
如下，输入为一张2828图片，拆解成2828=784个特征，最终经过三个线性层（784，128）、（128、64）、（64，10），输出为10个特征（对应10个类），归一化这10个特征，它们的大小即认为它属于哪张图片的概率值，取出概率最大的特征对应的类别作为最终预测类别。

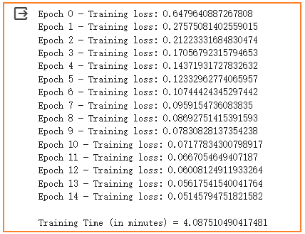
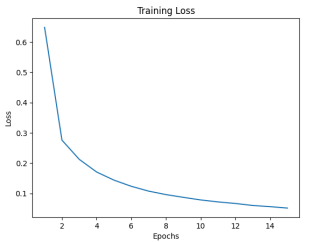
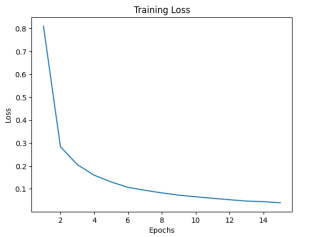
模型训练：

模型评估：
准确率：达到97.69%

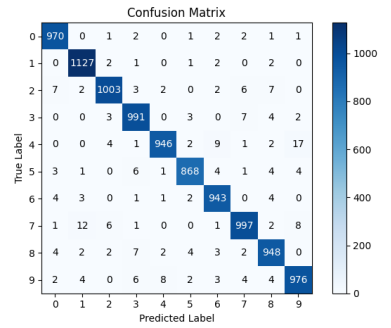
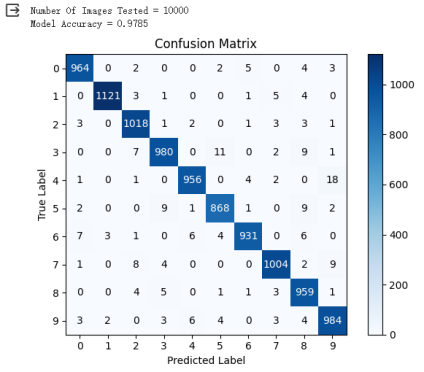
混淆矩阵

接下来，分析网络层数对分类准确率的影响。
被对照试验：隐藏层数目改为2，神经元数目分别为128、64
准确率为：97.69%
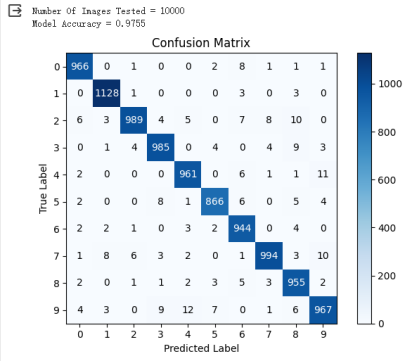
对照实验1：隐藏层数目改为3，神经元数目分别为256、128、64

Loss图：

准确率和混淆矩阵如下：97.55%

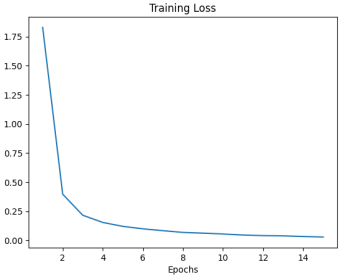
对照实验2：隐藏层数目改为5，神经元数目分别为512、256、128、64、32

Loss图：

准确率和混淆矩阵：97.85%

总结结果如下表：

分析可知：

• 运行时间：从实验结果来看，在增加隐藏层数的情况下，运行时间明显增加。
• 准确率：实验结果显示，在增加隐藏层数的情况下，准确率大体上有所提升，但是总体变化幅度并不大，可能是因为epochs或者随机梯度下降等参数已经设为较优值，使得准确率已经接近最优效果，从而导致增加网络层数的提优空间并不明显。
  综合来看，增加隐藏层数对于提高分类准确率有一定的帮助，但是也会明显增加运行时间。其次，需要注意的是，若增加隐藏层数并非一定能够带来准确率的提升，过多的隐藏层可能会导致过拟合等问题。

🧡🧡实验总结🧡🧡

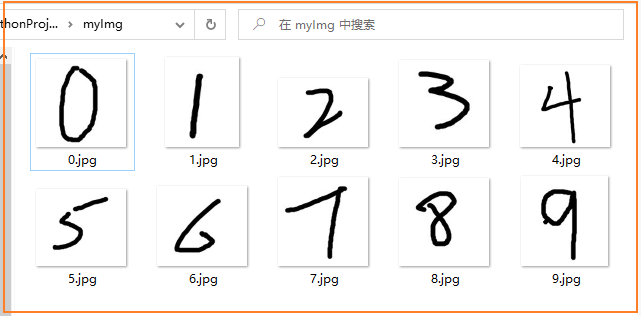
在完成基础实验上，我自己画了几张数字图，以对模型进行验证

结果如下，可以看到，对数字1和数字5分类错误（分布预测成了5和8），其余均分类正确，大体上效果良好。考虑原因，可能是因为minst的数据集是“黑底白字”，而我手画的图片则为“黑字白底”，导致了一些误差。

理论理解：
通过本次实验，大体上掌握了BP神经网络的定义和结构，总的来说，BP神经网络可以理解为一个黑盒子，通过不断根据loss进行反向传播，最终目的就是得到线性参数w和b，从而根据Y=wx+b 对输入的新x进行预测分类。
代码实践：
一开始想用纯numpy进行BP网络的编写，但是在编写后向传播时，可能是线代和高数知识有些遗忘，求导数时琢磨了很久。后面还是选择直接使用pytorch进行编写，也容易调参，方便进行实验。对我而言，代码中比较纠结的是shape的转换和传入，因此最好多查看中间过程的shape，以便更好理解。