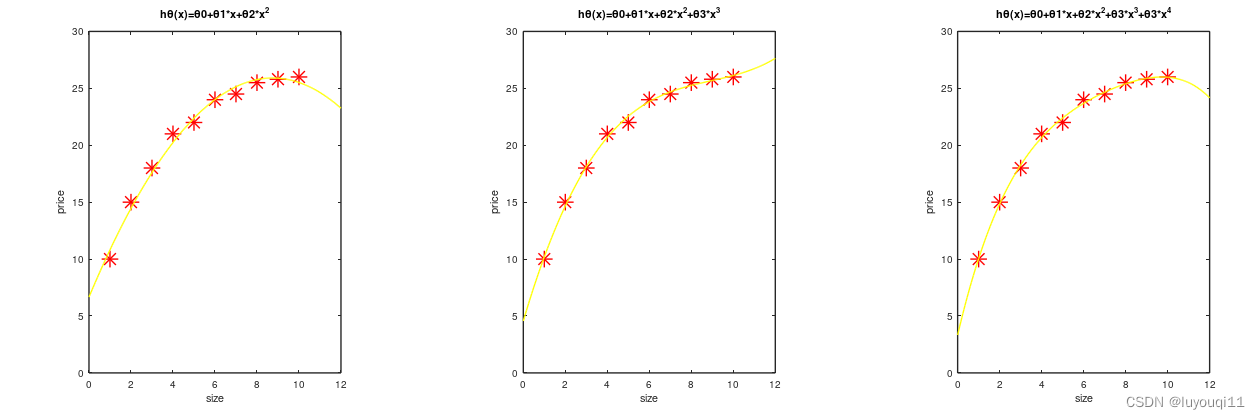
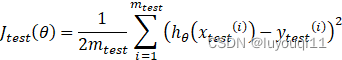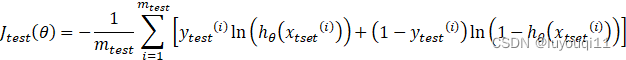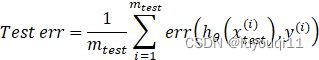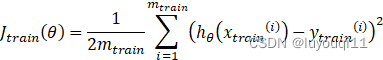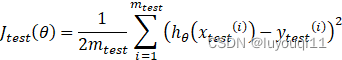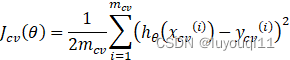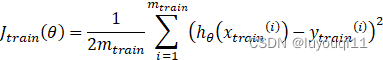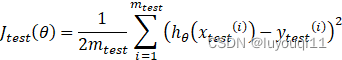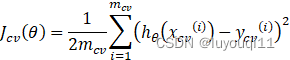对于一个给定的训练集，我们可以有很多假设模型。都可以完美拟合训练集的样本。但是哪一种模型最好呢？

1. 若预测时的输入值，不在训练集内，得到的预测值与实际趋势偏差过大，就是不好的假设模型（欠拟合、过拟合）
2. 若预测时的输入值，不在训练集内，得到的预测值与实际趋势偏差正常，就是好的假设模型

分为两个主题，（1）就是一个测试模型是否准确时，对于采集到的训练样本集的一般处理方法（切割为训练集、测试集）；（2）线性回归、逻辑回归对于测试集的预测效果的衡量公式。

1 分割样本为训练集和测试集

对于得到所有的样本，我们将：

1. 其中的70%作为训练样本，用于建立假设模型，叫做训练集。
2. 其中的30%作为测试样本，用于验证假设模型的准确程度，叫做测试集。

若测试集的偏差不大，就是好的假设模型。

若测试集的偏差过大，就是过拟合。

2 对于测试集的预测效果的衡量公式

线性回归

Step1：根据训练样本找到使损失函数最小的一组参数θ

Step2：计算测试集的误差，即按照一定的方法计算上一步得到的模型对于测试集中自变量的预测值与自变量相对应的因变量之间的差值，如下式：

逻辑回归

Step1：根据训练样本找到使损失函数最小的一组参数θ

Step2：计算测试集的误差，即按照一定的方法计算上一步得到的模型对于测试集中自变量的预测值与自变量相对应的因变量之间的差值，如下式：

Step3：误分类的误差计算。实际上很简单的公式来计算：

                                                                     otherwise

上式的意思就是，如果某个测试样本被系统分类分错了，就是逻辑回归的计算值与该测试样本的实际y值不同，则这个点取值为1（否则，正确取值为0），然后把所有的m_test个测试样本的预测是否正确的结果全部加起来，来衡量逻辑回归模型对这个测试集的样本预测错误的大小。

3 诊断偏差(bias)和方差(variance)

怎样快速判断不好的机器学习算法导致了高偏差还是高方差？

当一个算法出现问题时，多数是两种情况：（1）偏差太大；（2）方差太大。即要么欠拟合、要么过拟合。

那，如果在使用机器学习算法时效果不理想，那能够搞明白到底是偏差太大还是方差太大抑或两者都太大那就显得比较重要了。这样就能够有针对性的改进我们的算法了。

利用上节介绍的交叉验证集。计算训练误差和验证集的误差。我们看看多项式的最高次幂d和误差之间的关系曲线是怎样的。

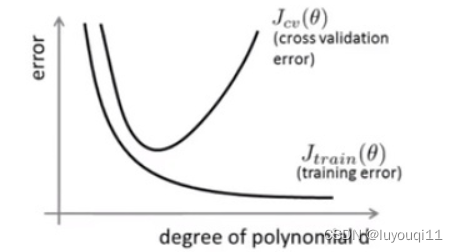
我们知道，针对训练集，训练误差会随着d的增加越来越小（过拟合）。那验证误差怎样呢？当过拟合发生的时候，验证误差就会随着d的增加而增加。如下图中间的图形，蓝色为训练误差，红色为验证误差。坐标的横轴为d、纵轴为误差大小。以线性回归为例：

训练误差

验证误差（又可称为交叉验证误差Cross validation error）

多项式最高次幂d和误差的关系曲线，如下图。

当你算法未达到预期的时候，到底是出现了高偏差还是高方差呢？

一般情况下，左侧一端对应的是高偏差、另一边对应的是高方差。也就是说d小的时候欠拟合带来高偏差、d较大的过拟合容易引起高方差。

1. 高偏差（欠拟合）：训练误差会较大，而且训练误差和验证误差会比较接近。
2. 高方差（过拟合）：训练误差会较小，而验证误差就会远大于训练误差。

其实很简单，就是对比训练误差和验证误差的大小关系就大致能判断出模型是欠拟合还是过拟合，然后就可以采取对应的措施（例如多项式拟合，就可以通过不断尝试找到合适的d）。

4 正则化对偏差和方差的影响

我们学过如何使用正则化防止过拟合，那这个正则化和算法的偏差/方差又有什么关系呢？

为了防止过拟合，线性回归的代价函数被叠加了一个正则化部分。如下：

模型：

代价函数：

通过前面我们知道，多项式拟合的阶数选择不合理会加大偏差、方差。

那正则化式中，λ取值不合适也会对偏差、方差造成影响。看两种极端情况：

1. λ非常大，那代价函数的取值受正则化项影响过大，最后得到的拟合公式就会产生严重的欠拟合，
2. λ非常小，正则项对代价函数影响不大，容易产生过拟合，λ=0
3. 只有当λ取值适中时，才会有较好的拟合效果，如上图中间。

4.1 如何选择合适的λ？

模型：

代价函数：

根据上面的模型公式，找到训练集、验证集、测试集的优化目标。

与找多项式阶数类似的方法，我们设置一个λ可能的取值区间，然后以一定的步长去试最好的那个λ。比如：

1. Try 1：λ=0
2. Try 2：λ=0.01
3. Try 3：λ=0.02
4. Try 4：λ=0.04
5. Try 5：λ=0.08
6. Try 6：λ=0.12
7. Try 7：λ=0.32
8. Try 8：λ=0.64
9. Try 9：λ=1.28
10. Try 10：λ=2.56
11. Try 11：λ=5.12
12. Try 12：λ=10.24

针对上面案例的算法步骤如下：

Step1：使用训练集训练出12个不同程度的正则化模型，每个λ一个；

Step2：使用12个模型分别对交叉验证集计算出验证误差；

Step3：得出交叉验证误差最小的那个模型；

Step4：使用Step3中得到的模型计算测试集上的误差，看是否能够推广。

4.2 λ和偏差/方差的关系曲线 

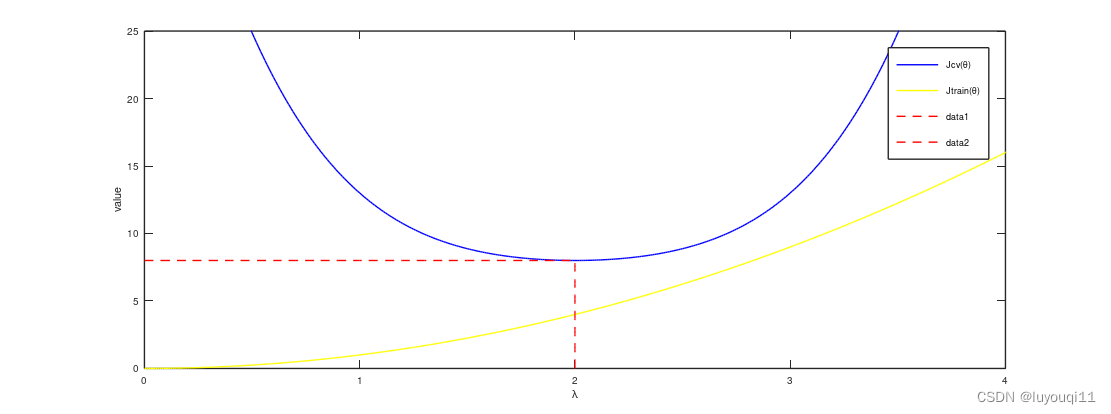
当改变λ时，误差肯定会跟着变化，具体的训练误差、验证误差随着λ的变化趋势是怎样的呢？以λ为横轴，以误差为纵轴，得到的曲线如下图右侧:

如上图，

1. 横轴是λ，纵轴是error值，
2. 蓝色线是交叉验证误差，左边表示高方差，右边表示高偏差
3. 黄色线是训练误差,
4. 只有λ取值适中的时候才会同时得到相对较小的训练误差和交叉验证误差

当然，在我们实际的实验中得到的曲线肯定会比上图中画的曲线波动要大得多，会有很多噪声干扰。

5 学习曲线

如果你想检验你的学习算法是否允许正常，或者想改进你的学习算法，那就很有必要绘制学习曲线。学习曲线还可以帮助我们查看算法结果是否有偏差、方差问题。

5.1 什么是学习曲线

一般先绘制训练集、验证集的误差曲线。

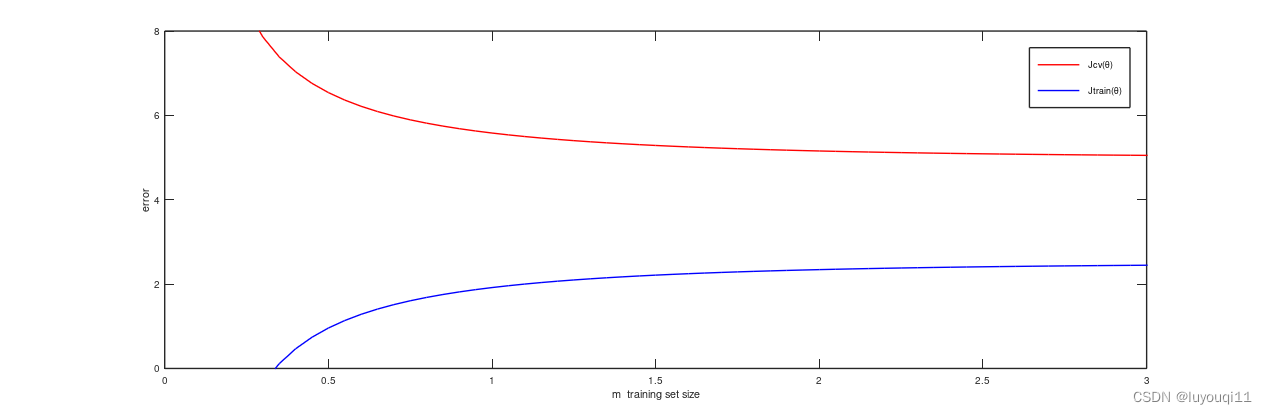
以训练集的学习曲线为例，以训练集样本的数目m为横坐标，以平均误差平方和为纵坐标绘制曲线，观察训练误差随训练样本集大小变化之间的关系。

如果我们有100个样例的训练集，我们会刻意改变训练集的大小m（比如，m=10,20,30,...,100)，当m变化时训练集的平均误差平方和也会跟着变化，这样就可以观察我们的算法随着训练集大小的变化其在训练集上的平均误差平方和方面的表现。

一般情况下，随着训练样本的增加，训练集的平均误差平方和会增加，而相应的验证集上的平均误差平方和会减少。

5.2 高偏差情形下的学习曲线

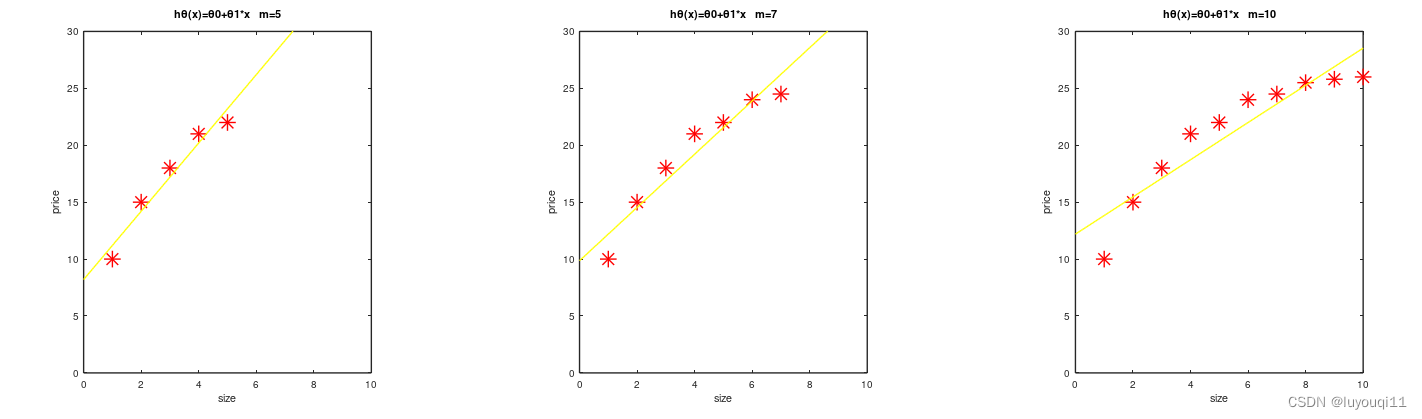
假设出现高偏差情况，假设使用的是线性模型，有下图所示的拟合效果（如下图，上半部分m取值较小，下半部分m取值较大）。θ

左边的m=5，中间的m=7，右边的m=10

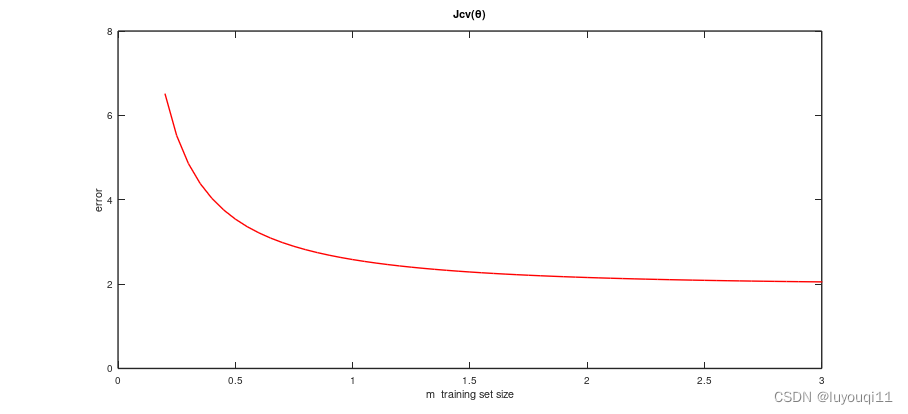
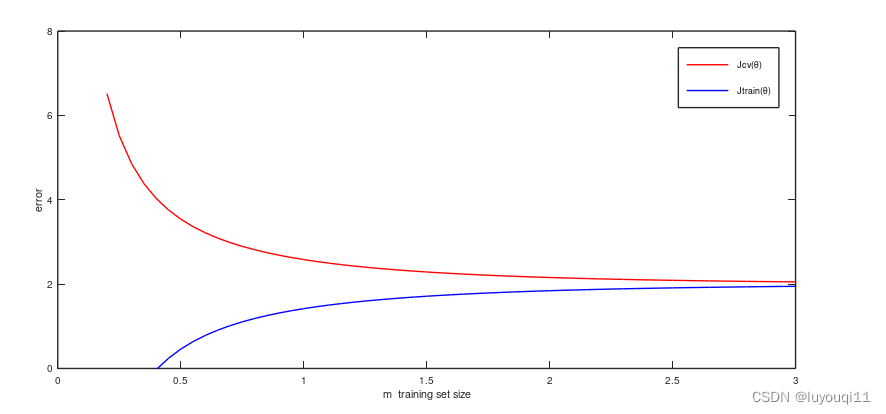
不停地改变m的值，会得到一条这样的曲线（验证集上的平均误差平方和）

你会发现如果在高偏差情况，随着m的增加验证集上的误差会减少，但是减少到一定程度之后m再增加误差就不会再有明显下降了。

同时，训练集上的平均误差平方和会随m增加而增加，且慢慢的非常接近验证集上的误差。

5.3 高方差情形下的学习曲线

下面，我们增加模型的复杂度，用更高项的多项式来拟合。

拟合曲线很曲折，在训练集上的表现很美妙。

训练集上的误差会一直较小，而验证集上的误差呢？却迟迟下不来。

从上面的曲线可以看出，如果我们的模型过于复杂，出现高方差，这种情形下如果继续增加训练样本的数量会使得算法变得更好。这也是为什么一些较复杂的算法，在普通量级的训练样本上表现一般般，一旦到了大数据领域就会有惊艳表现。

当然本文中的学习曲线是理想化后的，在实际工作中，学习曲线会有跳动，但一般来说画学习曲线可以使我们对我们设计的算法有个较好的认识。

6 总结

前面已经学习了如何评价学习算法，讨论了学习算法的偏差、方差，学了学习曲线。那所有这些东西怎样帮助我们改进我们的学习算法呢？

我们设计的算法如果不好，那它会有一些不符合我们预期的表现。比如较高的偏差，或者较高的方差等。那出现这些情况的时候我们该做一下怎样的改进呢？

6.1 算法不理想的时候能做的一些尝试

还是看看以前卖房子的例子，假设你设计的房价预测算法很不理想，那该怎么做呢？你可能会有很多种选择：

1. 收集更多的训练样本，扩大训练集；
2. 减少特征数量，去除一些和结果不相关的特征；
3. 增加特征数量，增加一些可能和结果相关但是被忽略的特征；
4. 增加多项式特征，比如等；
5. 减小正则化系数 λ
6. 加大正则化系数λ

如果上面可能选择的工作都做一遍的话，显然会耗费大量时间和精力。那到底怎样做才算有的放矢呢？这就要结合算法在交叉验证集或测试集上的具体表现来选择合适的改进方案。

1. 收集更多的训练样本，扩大训练集；——往往用来解决高方差问题
2. 减少特征数量，去除一些和结果不相关的特征；——往往用来解决高方差问题
3. 增加特征数量，增加一些可能和结果相关但是被忽略的特征；——往往用来解决高偏差问题
4. 增加多项式特征，比如等；——往往用来解决高偏差问题
5. 减小正则化系数λ——往往用来解决高偏差问题
6. 加大正则化系数λ——往往用来解决高方差问题

6.2 神经网络和过拟合问题

神经网络的优化主要是对其结构的优化，输入、输出的选择，中间层神经元个数的确定、隐藏层的设计等。

当使用神经网络解决一些问题的时候，有两种选择，用比较简单的网络或用比较复杂的网络。

但是小网络容易出现欠拟合，而大网络容易出现过拟合且运算量会非常大。那咋办呢？

1. 如果你经常使用神经网络的话，你会发现往往神经元个数越多的网络可能效果越好，如果出现过拟合的话可以使用正则化项进行修正。
2. 另外一个要处理的是选择隐藏层的个数，用3个还是2个？这是一个问题。这个时候就可以把你的训练数据拆分成训练集、交叉验证集、测试集三个子集，然后变换隐藏层的个数，再看不同隐藏层个数的网络在验证集上的表现来进行隐藏层的设定。

7 示例【Python】实现方差与偏差 

实现正则化线性回归，使用其来研究具有不同偏差-方差属性的模型。

分为两个部分：前半部分，将使用水库水位的变化实现正则化线性回归来预测大坝的出水量。在下半部分中，将对调试学习算法进行诊断，并检查偏差和方差的影响。

7.1 数据集ex5data1.mat

本次的数据是以.mat格式储存的，x表示水位的变化，y表示大坝的出水量。数据集共分为三部分：训练集（X, y）、交叉验证集（Xval, yval）和测试集（Xtest, ytest）。

7.2 Python代码

#################################################################
## Part 1 使用水库水位的变化实现正则化线性回归来预测大坝的出水量#
#################################################################
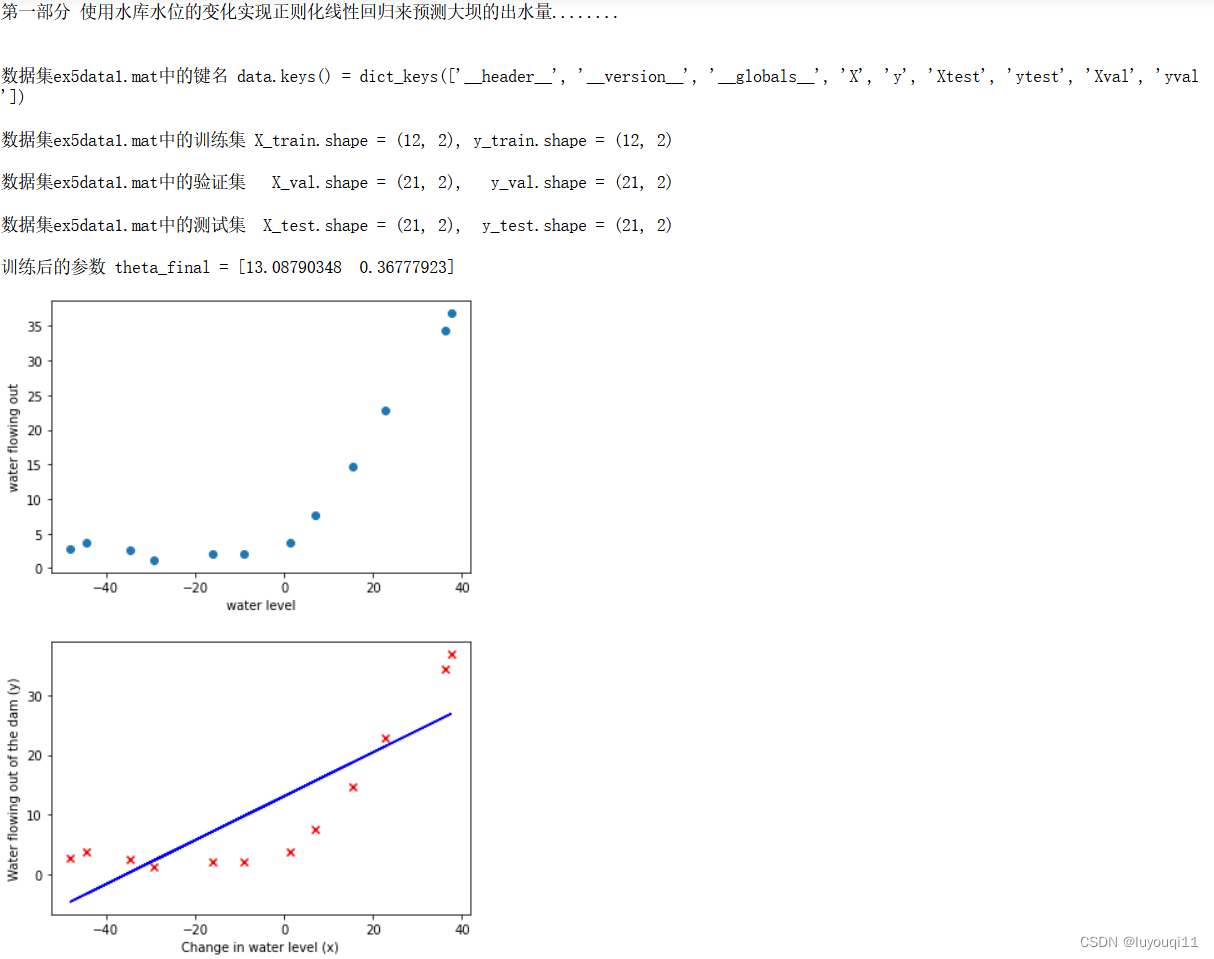
print('\n第一部分 使用水库水位的变化实现正则化线性回归来预测大坝的出水量........\n')

# 第一步 导入数据及可视化
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio

fileName =  'ex5data1.mat'
data = sio.loadmat(fileName)
print(f'\n数据集{fileName}中的键名 data.keys() = {data.keys()}')
 
X_train, y_train = data['X'], data['y']           # 训练集（12，1）
X_val, y_val = data['Xval'], data['yval']      # 验证集 （21，1）
X_test, y_test = data['Xtest'], data['ytest'] # 测试集 (21,1）

# 输入特征加入截距项，在第一列前插入全1的列
X_train = np.insert(X_train, 0, 1, axis=1)
X_val = np.insert(X_val, 0, 1, axis=1)
X_test = np.insert(X_test, 0, 1, axis=1)
print(f'\n数据集{fileName}中的训练集 X_train.shape = {X_train.shape}, y_train.shape = {X_train.shape}')
print(f'\n数据集{fileName}中的验证集   X_val.shape = {X_val.shape},   y_val.shape = {X_val.shape}')
print(f'\n数据集{fileName}中的测试集  X_test.shape = {X_test.shape},  y_test.shape = {X_test.shape}')
 
def plot_data():
    fig, ax = plt.subplots()
    ax.scatter(X_train[:, 1], y_train)
    ax.set(xlabel="water level", ylabel="water flowing out")
 
plot_data()

# 第二步 定义损失函数
# 2.1 定义损失函数
def reg_cost(theta, X, y, lamda):
    cost = np.sum(np.power((X @ theta - y.flatten()), 2))#对y进行降维
    reg = np.sum(np.power(theta[1:], 2)) * lamda
    return (cost + reg) / (2 * len(X))
 
# 2.2 定义梯度函数
def reg_gradient(theta, X, y, lamda):
    grad = (X @ theta - y.flatten()) @ X
    reg = lamda * theta
    reg[0] = 0#第一项不做正则化
    return (grad + reg) / (len(X))

# 第三步 神经网络训练参数并可视化lmd=0时拟合的线性方程
# 3.1 定义训练参数函数
from scipy.optimize import minimize
def train_model(X,y,lamda):
    theta = np.ones(X.shape[1])
    res = minimize(fun = reg_cost,
                   x0 = theta,
                   args = (X,y,lamda),
                   method = 'TNC',
                   jac = reg_gradient)
    return res.x   #易错！！！！记得返回x！！！！！！

# 3.2 得到训练后的参数
theta_final = train_model(X_train,y_train,lamda = 0)
print(f'\n训练后的参数 theta_final = {theta_final}')  #[13.0879035   0.36777923]

# 3.3 拟合图像
fig,ax = plt.subplots()
plt.scatter(X_train[:, 1], y_train, c='r', marker='x')
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam (y)')  
plt.plot(X_train[:,1],X_train@theta_final,c = 'b')
plt.show()

# 3.4 拟合曲线显示拟合的不是很好，由第四步绘制出lamda = 0的学习曲线可以看出存在高偏差问题。
#   若二者损失都大且差距不明显，则设定的模型过于简单，无法很好的拟合数据，存在欠拟合问题。

# 第四步  画学习曲线，判断高偏差、高方差问题
#   训练样本从开始递增进行训练，比较训练集和验证集上的损失函数的变化情况,
#   学习曲线用来判断样本存在高偏差/高方差的情况
#   若二者损失都大且差距不明显，则为高偏差，训练集低损失而验证集高损失，说明高偏差
#   利用选择不同的lamda来解决问题，高偏差减小lamda,高方差增大lamda

# 4.1 定义绘制学习曲线函数
def plot_learning_curve(X_train,y_train,X_val,y_val,lamda):
    train_cost = []
    cv_cost = []
    x = range(1,len(X_train+1))
    
    for i in x:#x (1-13)
        res = train_model(X_train[:i,:],y_train[:i,:],lamda)
        #res0 = list(res.values()) #将优化后的参数字典中的数值转为列表
        #res_ = res0[0]#提取参数字典中的theta
        training_cost_i = reg_cost(res,X_train[:i,:],y_train[:i,:], lamda)
        cv_cost_i = reg_cost(res,X_val,y_val, lamda)
        train_cost.append(training_cost_i)
        cv_cost.append(cv_cost_i)
 
    plt.plot(x,train_cost,label = 'training cost')
    plt.plot(x,cv_cost,label = 'cv cost')
    plt.legend(loc = 1)
    #plt.xlim(0, 12)
    #plt.ylim(0)
    plt.xlabel('number of training examples')
    plt.ylabel('costs')
    plt.show()
    return

# 4.2 绘制学习曲线（不考虑正则化的情况，出现欠拟合的情况）
#   可以看出，二者损失都较大，高偏差，因此特征映射创造多项式特征，
#   进行多项式回归，用更复杂的函数去拟合
plot_learning_curve(X_train,y_train,X_val,y_val,lamda = 0) # lmd = 0,表示误差

# 第五步 特征映射  均值归一化

# 5.1 定义多项式特征函数

#     增加多项式，从x的平方到x的多次方
def poly_feature(X, power):
    for i in range(2, power + 1):#从二次方到power次方
        X = np.insert(X, X.shape[1], np.power(X[:, 1], i), axis=1)#从第二列开始插入多列多项式
    return X
 
# 5.2 定义获取均值和方差函数
def get_standard(X):
    # 按行计算，即求每一列的均值和方差
    means = np.mean(X, axis=0)
    stds = np.std(X, axis=0)
    return means, stds
 
# 5.3 定义标准化函数
def feature_normalize(X, means, stds):
    X[:, 1:] = (X[:, 1:] - means[1:]) / stds[1:]#取所有行，去掉第一列
    return X

# 5.4  测试，最大六次方
power = 6
lamda = 0

# 5.4.1 特征映射
X_train_poly = poly_feature(X_train, power)
X_val_poly = poly_feature(X_val, power)
X_test_poly = poly_feature(X_test, power)

# 5.4.2 标准化
train_means, train_stds = get_standard(X_train_poly)
X_train_norm = feature_normalize(X_train_poly, train_means, train_stds)
X_val_norm = feature_normalize(X_val_poly, train_means, train_stds)
X_test_norm = feature_normalize(X_test_poly, train_means, train_stds)

# 5.4.3 训练后得到参数
theta_fit = train_model(X_train_norm, y_train, lamda)
print(theta_fit)

# 第六步 绘制多项式回归的拟合曲线

# 6.1 定义绘制多项式回归的拟合曲线函数
def plot_poly_fit():
    plot_data()
    x = np.linspace(-60, 60, 100)#生成网格数据（100，）
    xReshape = x.reshape(100, 1)#从（100，）到（100，1）
    xReshape = np.insert(xReshape, 0, 1, axis=1)#插入第一列1
    xReshape = poly_feature(xReshape, power)#特征映射
    xReshape = feature_normalize(xReshape, train_means, train_stds)#标准化
 
    plt.plot(x, xReshape @ theta_fit, 'r--')  #曲线  （x,xx@thte）
    plt.show()
    return
 
# 6.2 绘制多项式回归的拟合曲线
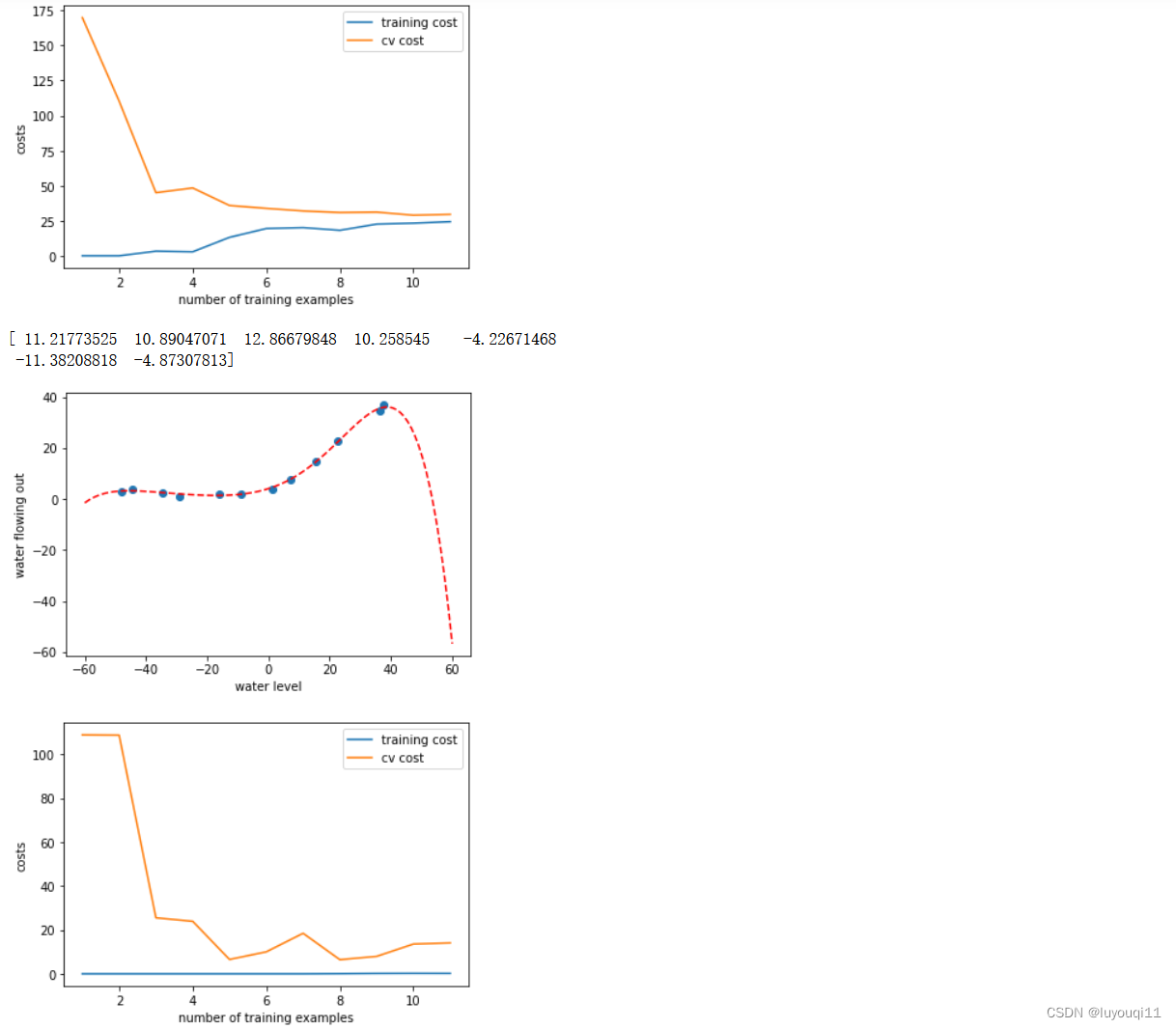
plot_poly_fit()

# 第七步 显示不同lamda取值下的学习曲线

# 7.1 高方差，次数太多，过拟合
plot_learning_curve(X_train_norm, y_train, X_val_norm, y_val, lamda=0)

# 7.2 加入正则化
plot_learning_curve(X_train_norm, y_train, X_val_norm, y_val, lamda=1)

# 7.3 正则化很大，欠拟合
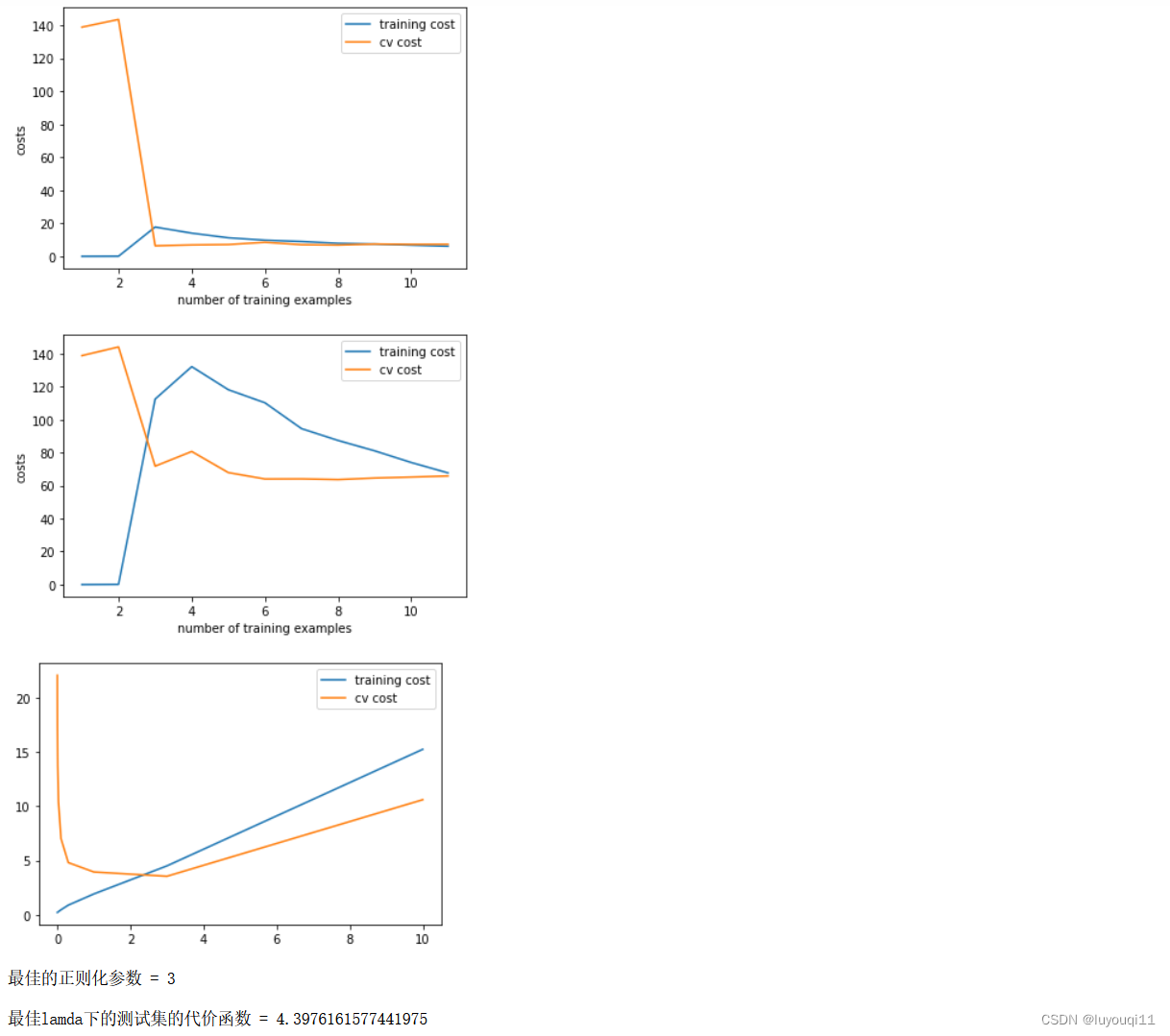
plot_learning_curve(X_train_norm, y_train, X_val_norm, y_val, lamda=100)

# 第八步 用交叉验证集选择最佳lmd

# 8.1 用交叉验证集选择lmd
lamdas = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
training_cost = []
cv_cost = []
for lamda in lamdas:
    res = train_model(X_train_norm, y_train, lamda)
    tc = reg_cost(res, X_train_norm, y_train, lamda=0)#计算训练集上的误差
    cv = reg_cost(res, X_val_norm, y_val, lamda=0)#计算验证集上的误差
 
    training_cost.append(tc)
    cv_cost.append(cv)
 
plt.plot(lamdas, training_cost, label='training cost')#不同lamda取值下训练集的损失
plt.plot(lamdas, cv_cost, label='cv cost')
plt.legend()
plt.show()
 
# 8.2 拿到最佳lamda
bestLamda = lamdas[np.argmin(cv_cost)]
print(f'最佳的正则化参数 = {bestLamda}')

# 8.3 用最佳lamda来训练测试集
res = train_model(X_train_norm, y_train, bestLamda)
cost = reg_cost(res, X_test_norm, y_test, lamda=0)
print(f'\n最佳lamda下的测试集的代价函数 = {cost}')#4.3976161577441975

运行结果如下：