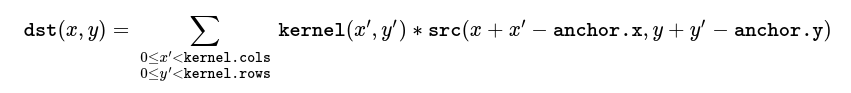（七）图像处理中常用算子Laplacian\Sobel\Roberts\Prewitt\Kirsch

1.拉普拉斯(Laplacian)算子

1.1基础介绍

最简单的各向同性导数算子是拉普赖斯算子，其具有旋转不变性，对于两个变量的函数 $f (x, y)$ ,其定义为
$\triangledown^2f=\frac{\partial ^2f}{\partial x ^2} + \frac{\partial ^2f}{\partial y ^2}$ ,以离散形式表示上述公式为：
<br/>x方向有：$\frac{\partial ^2f}{\partial x ^2} = f(x+1, y) + f(x-1, y) - 2f(x,y） = (f(x+1, y) -f(x,y)) - (f(x,y)-f(x-1,y))
$‘ < b r / > ‘ y 方向有$ \frac{\partial ^2f}{\partial y ^2} = f(x, y+1) + f(x, y-1) - 2f(x,y）$
由上面的公式，离散形式的拉普拉斯变换为:

$\triangledown ^2f(x,y) = f(x, y+1) + f(x, y-1)+f(x+1, y) + f(x-1, y) - 4f(x,y）$

使用卷积核的形式可表示为：
$\begin{bmatrix} 0& 1 & 0\\ 1& -4 & 1 \\ 0 & 1 & 0 \end{bmatrix}$

拉普拉斯算子是图像的二阶梯度算子，在灰度恒定区域其结果为0，在像素均匀变化区域其结果也为0，在像素变化速率变化较大区域其值也会变大，因此可将拉普拉斯算子应用到图像锐化和边缘检测。

应用到图像锐化时，应用拉普拉斯算子后的结果丢失了恒定像素区域的信息，因此将其与原图相加可求得锐化后的图像。(负中心就减正中心就加)。

1.2OpenCV API

Laplacian见OpenCV文档

void cv::Laplacian(
    InputArray 	src,
    OutputArray 	dst,
    int 	ddepth,
    int 	ksize = 1,
    double 	scale = 1,
    double 	delta = 0,
    int 	borderType = BORDER_DEFAULT 
)

src原图
dst结果，与原图同shape
ddepthDesired depth目标图像的深度
ksize卷积核的大小，正奇数
scale可选的计算拉普拉斯值时的缩放因子
delta可选的计算拉普拉斯值时需加的值
borderType像素外推方法，不支持BORDER_WRAP

1.3 示例

void laplacianOperator(cv::Mat &img) 
{
    int kernel_size = 1;
    int scale = 1;
    int delta = 0;
    int ddepth = CV_16S;
    const char* window_name = "Laplace Demo";

    cv::GaussianBlur(img, img, cv::Size(3, 3), 0, 0, cv::BORDER_DEFAULT);

    cv::Mat img_gray;
  
    cv::cvtColor(img, img_gray, cv::COLOR_BGR2GRAY);
    cv::Mat dst;
    cv::Laplacian(img_gray, dst, ddepth, kernel_size, scale, delta, cv::BORDER_DEFAULT);

    cv::Mat dst_abs;
    // converting back to CV_8U
    cv::convertScaleAbs(dst, dst_abs);
    cv::Mat compound_img;
    cv::Mat imageEnhance;
    cv::Mat kernel = (cv::Mat_<float>(3, 3) << 0, 1, 0, 1, -4, 1, 0, 1, 0);
    cv::filter2D(img_gray, imageEnhance, CV_8UC3, kernel);
    cv::imshow("filter2D", imageEnhance);

    cv::subtract(img_gray, imageEnhance, compound_img);

    cv::imshow("Origin: ", img_gray);
    cv::imshow(window_name, dst_abs);
    cv::imshow("compound_img: ", compound_img);
    cv::waitKey(0);
    cv::imwrite("origin_image.png", img_gray);
    cv::imwrite("laplacian.png", dst_abs);
    cv::imwrite("enchanced_image.png", compound_img);
}

原图：

在这里插入图片描述

应用拉普拉斯算子后的二阶梯度图：

在这里插入图片描述

锐化后的图像:
在这里插入图片描述

2.Sobel算子

2.1基础

在进行边缘检测时需先求出图像的梯度，在像素的每个位置计算偏导数 $\frac{\partial f}{\partial x}$ 和 $\frac{\partial f}{\partial y}$ ，图像的梯度计算，通常使用前向或中心有限差分。使用前向差分计算：<br/>
$g_x(x,y) = \frac{\partial f(x, y)}{\partial x} = f(x+1, y) - f(x, y)$
<br/>
$g_y(x,y) = \frac{\partial f(x, y)}{\partial y} = f(x, y+1) - f(x, y)$

上述梯度的计算可以使用一维核对 $f (x, y)$ 滤波实现。
$\begin{bmatrix} -1\\ 1 \end{bmatrix}$ 和 $\begin{bmatrix} 1\\ -1 \end{bmatrix}$

感兴趣的区域是对角边缘时，需要使用二维核。Sobel核在中心系数上使用了权值2，
$g_x = \frac{\partial f}{\partial x} = (z_7 + 2z_8 + z_9) - (z_1+2z_2+z_3)$ 和
$g_y = \frac{\partial f}{\partial y} = (z_3+2z_6+z_9)-(z_1+2z_4+z_7)$

$\begin{bmatrix} -1 & -2 & -1\\ 0& 0 & 0\\ 1& 2 & 1 \end{bmatrix}$
和
$\begin{bmatrix} -1 & 0 & 1\\ -2& 0 & 2\\ -1& 0 & 1 \end{bmatrix}$

在中心位置使用2可以平滑图像，Sobel算子只为垂直边缘和水平边缘给出各向同性的结果。

Sobel算子在kernel大小为3时,使用上述算子计算梯度会产生不可忽略的误差,对图像中较弱的边缘提取效果较差。为了能够有效的提取出较弱的边缘，需要将像素值间的差距增大，因此引入Scharr算子。Scharr算子是对Sobel算子差异性的增强。

$\begin{bmatrix} -3 & -10 & -3\\ 0& 0 & 0\\ 3& 10 & 3 \end{bmatrix}$
和
$\begin{bmatrix} -3 & 0 & 3\\ -10& 0 & 10\\ -3& 0 & 3 \end{bmatrix}$

2.2 OpenCV API


void cv::Sobel	(
    InputArray 	src,
    OutputArray 	dst,
    int 	ddepth,
    int 	dx,
    int 	dy,
    int 	ksize = 3,
    double 	scale = 1,
    double 	delta = 0,
    int 	borderType = BORDER_DEFAULT 
)

src输入图像
dst输出图像，与src同shape
ddepth输出图像深度
dxx偏导的阶
dyy偏导的阶
ksize``Sobel算子的大小
scale可选的梯度值的缩放因子
delta可选的梯度值的偏置
borderType边界值的处理方式，dst与src同尺寸，故需对src边界扩充，可用方式见BorderTypes，不支持BORDER_WRAP

2.3实例

void sobelOperator(cv::Mat &img)
{
    cv::GaussianBlur(img, img, cv::Size(5, 5), 0, 0, cv::BORDER_DEFAULT);
    cv::Mat img_gray;
    cv::cvtColor(img, img_gray, cv::COLOR_BGR2GRAY);
    cv::Mat grad, grad_x, grad_y, abs_grad_x, abs_grad_y;
    const cv::String window_name = "Sobel Demo - Simple Edge Detector";
    int ksize = 3;
    int scale = 1;
    int delta = 0;
    int ddepth = CV_16S; 
    cv::Sobel(img_gray, grad_x, ddepth, 1, 0, ksize, scale, delta, cv::BORDER_DEFAULT);
    cv::Sobel(img_gray, grad_y, ddepth, 0, 1, ksize), scale, delta, cv::BORDER_DEFAULT;

    cv::convertScaleAbs(grad_x, abs_grad_x);
    cv::convertScaleAbs(grad_y, abs_grad_x);
    cv::addWeighted(abs_grad_x, 0.5, abs_grad_x, 0.5, 0, grad);
    cv::imshow(window_name, grad);

    // cv::Mat kernel_x = (cv::Mat_<float>(3, 3) << -1, 0, 1, -2, 0, 2, -2, 0, 2);
    // cv::Mat kernel_y = (cv::Mat_<float>(3, 3) << -1, -2, -1, 0, 0, 0, 1, 2, 1);
    cv::Mat kernel_x = (cv::Mat_<float>(3, 3) << -3, 0, 3, -10, 0, 10, -3, 0, 3);
    cv::Mat kernel_y = (cv::Mat_<float>(3, 3) << -3, -10, -3, 0, 0, 0, 3, 10, 3);
    cv::Mat grad_k, grad_x_k, grad_y_k, abs_grad_x_k, abs_grad_y_k;
    cv::filter2D(img_gray, grad_x_k, ddepth, kernel_x, cv::Point(-1, -1), 0, cv::BORDER_DEFAULT);
    cv::filter2D(img_gray, grad_y_k, ddepth, kernel_y, cv::Point(-1, -1), 0, cv::BORDER_DEFAULT);
    cv::convertScaleAbs(grad_x_k, abs_grad_x_k);
    cv::convertScaleAbs(grad_y_k, abs_grad_y_k);
    cv::addWeighted(abs_grad_y_k, 0.5, abs_grad_x_k, 0.5, 0, grad_k);
    cv::imshow("Soble by Filtered2D", grad_k);
    cv::imshow("Origin", img_gray);
    cv::imwrite("sobel.png", grad);
    cv::waitKey(0);
}

梯度图像：
在这里插入图片描述

3.Roberts算子【1965】

3.1基本理论

罗伯特交叉梯度算子是最早使用具有对角性能的二维核的算子之一，罗伯特算子的实现方式为对角差分，x方向
$g_x = \frac{\partial f}{\partial x}=(z_9 -z_5)$ 算子为 $\begin{bmatrix} -1 &0 \\ 0& 1 \end{bmatrix}$ , y方向 $g_y = \frac{\partial f}{\partial y}=(z_8 -z_6)$ ，算子为 $\begin{bmatrix} 0&-1 \\ -1& 0 \end{bmatrix}$ ， 2x2的核概念上简单，但不如中心对称的核准确。

3.2OpenCV API

OpenCV中没有专门的函数实现Roberts算子。可以借助filter2D()函数实现

void cv::filter2D	(	
    InputArray 	src,
    OutputArray 	dst,
    int 	ddepth,
    InputArray 	kernel,
    Point 	anchor = Point(-1,-1),
    double 	delta = 0,
    int 	borderType = BORDER_DEFAULT 
)

src输入图像
dst与src同shape
ddepth目标图的深度，uint8等
kernel单通道卷积核，浮点矩阵，若想在不同的通道上使用不同的卷积核则将原图像按channel拆分，再使用不同的卷积核计算
anchor卷积的作用点，(-1, -1)表示卷积核的中心
delta 卷积后追加的偏置
borderType 边缘像素的处理方式

anchor的使用方式

在这里插入图片描述

3.3示例

void robertsOperator(cv::Mat &img)
{
    int ddepth = CV_16S;
    cv::GaussianBlur(img, img, cv::Size(5, 5), 0, 0, cv::BORDER_DEFAULT);
    cv::Mat img_gray;
    cv::cvtColor(img, img_gray, cv::COLOR_BGR2GRAY);
    cv::Mat kernel_x = (cv::Mat_<float>(2, 2) << -1, 0, 0, 1);
    cv::Mat kernel_y = (cv::Mat_<float>(2, 2) << 0, -1, 1, 0);
    cv::Mat grad_k, grad_x_k, grad_y_k, abs_grad_x_k, abs_grad_y_k;
    cv::filter2D(img_gray, grad_x_k, ddepth, kernel_x, cv::Point(-1, -1), 0, cv::BORDER_DEFAULT);
    cv::filter2D(img_gray, grad_y_k, ddepth, kernel_y, cv::Point(-1, -1), 0, cv::BORDER_DEFAULT);
    cv::convertScaleAbs(grad_x_k, abs_grad_x_k);
    cv::convertScaleAbs(grad_y_k, abs_grad_y_k);
    cv::addWeighted(abs_grad_y_k, 0.5, abs_grad_x_k, 0.5, 0, grad_k);
    cv::imshow("robert by Filtered2D", grad_k);
    cv::imshow("Origin", img_gray);
    cv::imwrite("roberts.png", grad_k);
    cv::waitKey(0);
}

在这里插入图片描述

4.Prewitt算子

4.1基本理论

Prewitt算子与Sobel算子十分类似，区别在于Sobel算子中心值为2，能够平滑噪声，Prewitt算子实现起来更简单，形如， x方向
和y方向分别为：
$\begin{bmatrix} -1 & 0 & 1\\ -2& 0 & 2\\ -1& 0 & 1 \end{bmatrix}$

$\begin{bmatrix} -1 & -2 & -1\\ 0& 0 & 0\\ 1& 2 & 1 \end{bmatrix}$

4.2OpenCV API

使用filter2D实现

4.3示例

void prewittOperator(cv::Mat &img)
{
    int ddepth = CV_16S;
    cv::GaussianBlur(img, img, cv::Size(5, 5), 0, 0, cv::BORDER_DEFAULT);
    cv::Mat img_gray;
    cv::cvtColor(img, img_gray, cv::COLOR_BGR2GRAY);
    cv::Mat kernel_x = (cv::Mat_<float>(3, 3) << -1, 0, 1, -2, 0, 2, -1, 0, 1);
    cv::Mat kernel_y = (cv::Mat_<float>(3, 3) << -1, -2, -1, 0, 0, 0, 1, 2, 1);
    cv::Mat grad_k, grad_x_k, grad_y_k, abs_grad_x_k, abs_grad_y_k;
    cv::filter2D(img_gray, grad_x_k, ddepth, kernel_x, cv::Point(-1, -1), 0, cv::BORDER_DEFAULT);
    cv::filter2D(img_gray, grad_y_k, ddepth, kernel_y, cv::Point(-1, -1), 0, cv::BORDER_DEFAULT);
    cv::convertScaleAbs(grad_x_k, abs_grad_x_k);
    cv::convertScaleAbs(grad_y_k, abs_grad_y_k);
    cv::addWeighted(abs_grad_y_k, 0.5, abs_grad_x_k, 0.5, 0, grad_k);
    cv::imshow("prewitt by Filtered2D", grad_k);
    cv::imshow("Origin", img_gray);
    cv::imwrite("prewitt.png", grad_k);
    cv::waitKey(0);
}

在这里插入图片描述

5.其他

此外还有Kirsch罗盘核，使用8个不同核，在8个方向上计算梯度，进行边缘检测

Tips

convertScaleAbs