最近在重温计算机图形学的基础知识,期望能做到温故知新,加深对其的理解,以便能从容应对工作中各种情况。
小弟水平有限,若有不正确之处,欢迎大家批评指正。
相关文章链接:
【计算机图形学基础】线性代数基础1
【计算机图形学基础】线性代数基础2
【计算机图形学基础】相机矩阵
【计算机图形学基础】投影矩阵
【计算机图形学基础】光照模型和着色频率
【计算机图形学基础】阴影映射
1. 相机矩阵的作用
将世界空间中的顶点,转换到相机空间中。使渲染的场景能够以相机的视角进行展示。
相机矩阵实际是特殊的模型矩阵。
2. 决定相机矩阵的因素
影响相机空间的因素有三个:
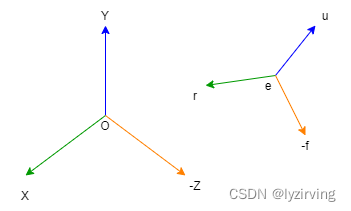
① 相机的位置(e):相机空间原点的位置。该位置默认与世界空间原点重合,即(0, 0, 0)。
② 相机的视线:即图中
−
f
⃗
-\vec{f}
−f 方向。
默认情况下,相机空间的
r
⃗
\vec{r}
r 和世界空间 +X 轴重合,
u
⃗
\vec{u}
u 和世界空间 +Y 轴重合,
f
⃗
\vec{f}
f 和世界空间 +Z 轴重合;
由于相机的视线为
−
f
⃗
-\vec{f}
−f 方向,所以在相机空间中,所有可见顶点的z值都是负数。
③ 相机的上方向
u
⃗
\vec{u}
u 。
综上,通过相机的位置和三轴方向,能够确认相机空间。
3. 相机三轴方向推导
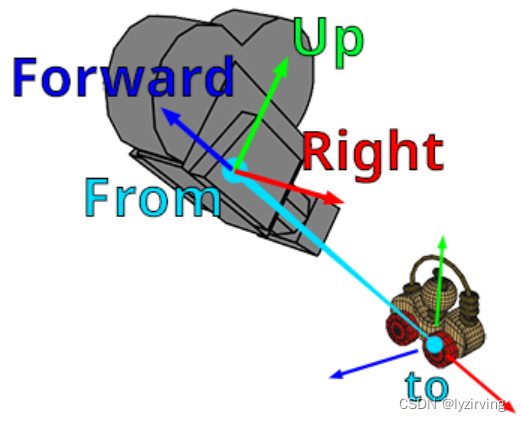
使用from指定相机在世界空间的位置;
使用to指定相机视线终点在世界空间的位置;
使用up指定相机的上方。
将from,up,to执行一定的数学计算,就可确定相机空间的三轴的方向。
forward向量(相机+z/+f轴):
vec3 forward = normalize(from - to)
right向量(相机+x/+r轴):不管forward如何变化,forward必然和世界空间的up(0, 1, 0)在同一个平面中,因此可以通过下式求出相机的right:
vec3 worldUp = normalize(vec3(0, 1, 0));
vec3 right = normalize(crossProduct(worldUp, forward));
up向量(相机+y/+u轴):right、up和forward满足右手法则,因此通过矩阵叉乘,就能求得up向量,注意叉乘的顺序:
vec3 up = normalize(crossProduct(forward, right));
综上,求得了相机三轴在世界空间中的方向。
4. 坐标转换公式
正交矩阵的所有列(行)向量构成了一个标准正交基(Orthonormal Bases),它的列向量(列主序)是两两垂直的单位向量。
标准正交基可以视为对坐标系的描述:在标准参考系下,同一向量
v
⃗
\vec{v}
v,在不同坐标基下,有不同的坐标。比如,
v
⃗
\vec{v}
v在坐标基
R
R
R下,坐标为
v
⃗
′
\vec{v}'
v′,在坐标基
Q
Q
Q下,坐标为
v
⃗
′
′
\vec{v}''
v′′:
v
⃗
=
R
v
⃗
′
=
Q
v
⃗
′
′
\vec{v}=R\vec{v}'=Q\vec{v}''
v=Rv′=Qv′′
有如下的示例:
(
1
2
6
)
=
(
1
0
0
0
1
0
0
0
1
)
(
1
2
6
)
=
(
0
0
1
1
0
0
0
1
0
)
(
2
6
1
)
\begin{pmatrix}1 \\ 2 \\ 6 \end{pmatrix} = \begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}1 \\ 2 \\ 6 \end{pmatrix} = \begin{pmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix}2 \\ 6 \\ 1 \end{pmatrix}
126
=
100010001
126
=
010001100
261
上述例子中,
(
1
0
0
0
1
0
0
0
1
)
\begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}
100010001
是正交基
R
R
R,同时也是通用的标准参考系,三轴分别为
(
1
,
0
,
0
)
(1, 0, 0)
(1,0,0)、
(
0
,
1
,
0
)
(0, 1, 0)
(0,1,0)和
(
0
,
0
,
1
)
(0, 0, 1)
(0,0,1)。
(
0
0
1
1
0
0
0
1
0
)
\begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix}
010001100
是正交基
Q
Q
Q,
(
2
6
1
)
\begin{pmatrix}2 \\ 6 \\ 1 \end{pmatrix}
261
是
v
⃗
\vec{v}
v在正交基
Q
Q
Q下的坐标
v
⃗
′
′
\vec{v}''
v′′。
可以看到,若某一坐标空间和标准参考系有相同的正交基,那么该坐标空间的正交基就是单位矩阵,因此有:
v
⃗
=
R
v
⃗
′
\vec{v}=R\vec{v}'
v=Rv′
所以得到坐标转换公式:
v
⃗
′
=
R
−
1
v
⃗
\vec{v}'=R^{-1}\vec{v}
v′=R−1v
由于R是正交矩阵,正交矩阵的逆矩阵等于其转置,故有:
v
⃗
′
=
R
T
v
⃗
\vec{v}'=R^{T}\vec{v}
v′=RTv
5. 相机矩阵推导
由第3小节《相机三轴方向推导》可以得到相机三轴(right、up和forward)在世界空间中的信息。
这三个两两垂直的单位列向量构成了一个正交基
R
c
a
m
=
(
r
⃗
u
⃗
f
⃗
)
R_{cam} =\begin{pmatrix}\vec{r} & \vec{u} & \vec{f} \end{pmatrix}
Rcam=(ruf),该正交基描述的正是相机空间坐标系。
由第4小节内容可知,应用坐标转换公式,有:
v
⃗
′
=
R
c
a
m
T
v
⃗
\vec{v}'=R_{cam}^{T}\vec{v}
v′=RcamTv
由于相机可能不在世界坐标的原点,因此还需要考虑相机的位移
T
T
T:在旋转前还需执行逆向移动。
v
⃗
′
=
R
c
a
m
T
T
c
a
m
−
1
v
⃗
\vec{v}'=R_{cam}^{T}T_{cam}^{-1}\vec{v}
v′=RcamTTcam−1v
综上,将世界空间的点变换到相机空间的矩阵为:
R
=
R
c
a
m
T
T
c
a
m
−
1
R = R_{cam}^{T}T_{cam}^{-1}
R=RcamTTcam−1
将矩阵展开,有:
R
=
(
r
x
r
y
r
z
0
u
x
u
y
u
z
0
f
x
f
y
f
z
0
0
0
0
1
)
(
1
0
0
−
T
x
0
1
0
−
T
y
0
0
1
−
T
z
0
0
0
1
)
R =\begin{pmatrix}r_{x} & r_{y} & r_{z} & 0 \\u_{x} & u_{y} & u_{z} & 0 \\ f_{x} & f_{y} & f_{z} & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}\begin{pmatrix}1 & 0 & 0 & -T_{x} \\ 0 & 1 & 0 & -T_{y}\\ 0 & 0 & 1 & -T{z}\\0 & 0 & 0 & 1\end{pmatrix}
R=
rxuxfx0ryuyfy0rzuzfz00001
100001000010−Tx−Ty−Tz1
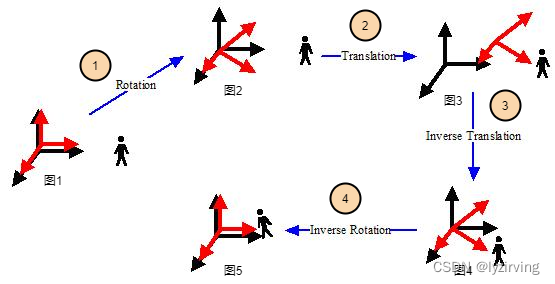
下图借鉴自popy007大佬的文章,很清晰的说明了这个过程:
图中黑色的正交基是通用的标准的参考系,红色的正交基是相机空间的坐标基。
步骤① 和步骤②先后将相机旋转、移动到指定姿态和位置,如图3所示。
此时对世界空间中所有的几何物体先后执行逆平移、逆旋转后,世界空间的所有几何体就被转换到了相机空间。