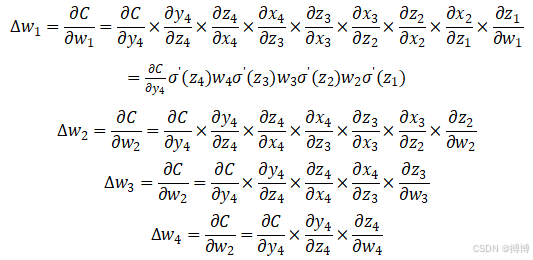神经网络问题之二：梯度爆炸（Gradient Explosion）

梯度爆炸（Gradient Explosion）是神经网络训练过程中常见的一个问题，它指的是在反向传播过程中，梯度值变得非常大，超出了网络的处理范围，从而导致权重更新变得不稳定甚至不收敛的现象。

一、产生原因

梯度爆炸问题通常发生在深度神经网络中，是深度神经网络的结构和训练过程中的一些固有特性，特别是当网络的层数较多、网络结构复杂时，或者使用了不合适的激活函数、初始化方法或优化算法时，随着网络层数的增加，梯度在反向传播过程中会逐层累积变化，这种变化可能导致梯度爆炸。

图1 梯度在反向传播过程中会逐层累积

具体原因包括：

深层网络：深度神经网络是多层非线性函数的堆砌，整个网络可以视为一个复合的非线性多元函数。在反向传播过程中，需要对这些函数求导，并应用链式法则。当层数较深时，梯度将以指数形式传播，如果接近输出层的激活函数求导后梯度值大于1，那么层数增多时，最终求出的梯度很容易指数级增长，从而产生梯度爆炸。
不合适的激活函数：某些激活函数（如sigmoid）在输入值过大或过小时，其导数会趋近于0，导致梯度消失；但在某些特定情况下（如输入值处于激活函数的饱和区），其导数也可能变得非常大，从而导致梯度爆炸。
不恰当的初始化方法：如果网络权重的初始化值过大，那么在反向传播过程中，梯度值可能会因为权重的累积效应而迅速增大，导致梯度爆炸。
优化算法问题：某些优化算法（如基于梯度的优化算法）在更新权重时，可能会因为步长过大或学习率设置不当而导致梯度爆炸。

二、示例说明梯度爆炸原因

1. sigmoid函数何时出现梯度爆炸

假设有如下图所示深度神经网络，每一层只有一个神经元，激活函数采用sigmoid函数。

图2 单神经元多层神经网络

前一层的输出和后一层的输入关系如公式所示：

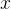
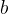
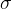
其中，是输入，是权重，是偏置， $\sigma$ 为激活函数sigmoid。

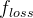
$f_{loss}$ 表示损失函数，表示损失函数的结果标量（预期结果与实际结果之间的误差）。具体为：

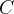
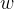
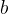
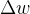
损失函数计算出误差之后，逐层往回传，对每一层的和进行梯度更新。而根据某一层权重的梯度 $\Delta w$ 等于损失函数对该层权重的偏导数，某一层偏置的梯度等于损失函数对该层偏置的偏导数，根据链式求导法则，我们可以推导出公式：

其中，关于“层输出”之间的求导，依如下方式求出：

不难发现，越接近输入层的梯度，计算时需要连乘的激活函数求导项和权重矩阵转置项就越多，因此，他们的梯度消失/爆炸也就会越明显。

而sigmoid函数的导数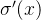 ${\sigma}'(x)$ 趋势如图3所示。

图3 sigmoid函数的导数趋势

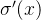
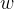
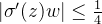
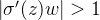
可见， ${\sigma}'(x)$ 的最大值为1/4，而我们一般会使用标准方法来初始化网络权重，即使用一个均值为0标准差为1的高斯分布。因此，初始化的网络权值通常（大部分）都小于1，从而有 $\left | {\sigma}'(z) w\right |\leq \frac{1}{4}$ 。对于2式的链式求导，层数越多，求导结果越小，最终导致梯度消失的情况出现。同时，如果有 $\left | {\sigma}'(z) w\right |> 1$ ，则会出现梯度爆炸。

2. sigmoid函数出现梯度爆炸的范围

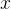
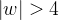
量化分析梯度爆炸时的取值范围：因导数最大为0.25，故 $\left | w \right |>4$ 才可能出现梯度爆炸，按照 $\left | {\sigma}'(wx+b) w\right |> 1$ 可计算出的数值变化范围很窄，仅在下面公式范围内，才会出现梯度爆炸。

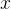
最大数值范围也仅仅0.45，当|w|=6.9时出现。因此仅仅在此很窄的范围内会出现梯度爆炸的问题。

三、神经网络训练的影响

梯度爆炸问题对神经网络训练的影响是显著的。当梯度爆炸发生时，网络的权重更新可能会变得异常大，导致网络的参数值迅速膨胀。这可能会导致数值溢出、计算错误和训练失败。此外，梯度爆炸还可能导致模型不稳定，使得训练过程中的损失值出现显著变化。

四、解决方法

为了解决梯度爆炸问题，可以采取以下措施：

权重衰减（Weight Decay）：通过给参数增加L1或L2范数的正则化项来限制参数的取值范围。这有助于防止权重值过大，从而减小梯度爆炸的风险。
梯度截断（Gradient Clipping）：当梯度的模大于一定阈值时，就将它截断成为一个较小的数。这有助于防止梯度值过大而导致的数值溢出和训练失败。
选择合适的激活函数：避免使用在特定输入范围内导数过大的激活函数。例如，可以选择ReLU及其变体等激活函数，这些函数在输入为正时具有恒定的导数，有助于缓解梯度爆炸问题。
合理的初始化方法：使用合适的权重初始化方法，如He初始化或Glorot初始化等。这些初始化方法可以根据网络的层数和激活函数的特点来设置权重的初始值，从而减小梯度爆炸的风险。
调整优化算法参数：合理设置优化算法的学习率、动量等参数。学习率不宜过大，以避免权重更新过快而导致的梯度爆炸；动量参数可以帮助稳定梯度更新过程，提高训练的稳定性。