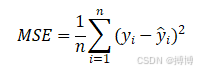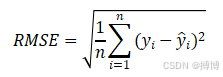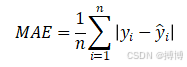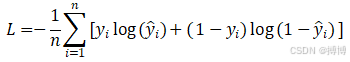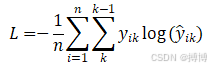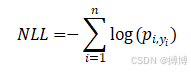神经网络中的损失函数（Loss Function）

损失函数（Loss Function）在机器学习和深度学习中扮演着至关重要的角色，它是衡量模型预测值与实际值之间差异程度的函数。通过最小化损失函数，我们可以优化模型的参数，使其预测结果更加准确。

一、损失函数的定义

损失函数（Loss Function）作为神经网络中的一个评估指标，用于衡量神经网络输出与真实标签之间的差异或误差。损失函数通常是一个非负实数函数，表示为L(Y, f(X))，其中Y是实际值（也称为标签或真实值），f(X)是模型的预测值（也称为输出值或估计值），X是输入数据。损失函数的值越小，表示模型的预测结果与实际值越接近，模型的性能也就越好。

二、损失函数的类型

根据任务的不同，损失函数有多种类型，常见的包括：

（一）回归任务

1. 均方误差（Mean Squared Error，MSE）

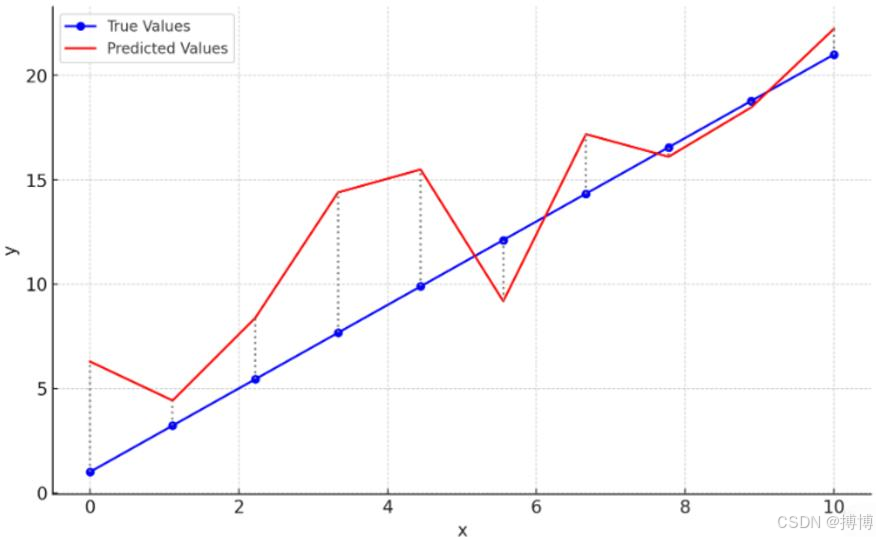
均方误差是机器学习和统计学中常用的一种损失函数，特别是在回归任务中。它用于衡量模型预测值与实际值之间的差异程度。MSE通过计算预测值与实际值之间差的平方的平均值来得出，因此它对大误差的惩罚较重。模型会倾向于避免大误差的出现。

图1 实际值和预测值之间的差异及其平方误差

（1）MSE的定义与公式

MSE是通过计算预测值与实际值之间差的平方的平均值来衡量的，其数学表达式为：

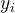
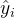
其中：是样本数量， $y_{i}$ 是第个样本的实际值（真实标签）。 $\hat{y}_{i}$ 是第个样本的预测值（模型输出）。

（2）MSE的特点

非负性：MSE的值总是非负的，因为平方运算的结果总是非负的。
敏感性：MSE对大误差的惩罚较重，因为误差的平方会放大较大的误差值。这有助于模型在训练过程中更加关注那些预测错误较大的样本。
可导性：MSE是连续且可导的，这使得它可以使用梯度下降等优化算法进行参数更新。
量纲一致性：MSE的值与数据本身的量纲相同（例如，如果数据是米，则MSE也是米²），这有时可能不太方便进行直观比较。为了消除量纲的影响，可以使用均方根误差（Root Mean Squared Error，RMSE）。

（3）MSE的应用

MSE广泛应用于各种回归任务中，如房价预测、股票价格预测、销量预测等。在这些任务中，模型的目标是尽可能准确地预测连续变量的值。通过最小化MSE，模型可以学习到输入特征与输出变量之间的最佳映射关系。

（4）MSE的局限性

尽管MSE在回归任务中非常有用，但它也有一些局限性：

对异常值敏感：由于MSE计算了所有误差的平方和的平均值，因此它对异常值（极端值）非常敏感。如果数据中存在异常值，MSE可能会变得很大，从而掩盖了其他样本的误差情况。
量纲问题：MSE的值与数据本身的量纲相同，这有时可能不太方便进行直观比较。为了消除量纲的影响，可以使用RMSE或其他无量纲的损失函数。
非鲁棒性：在某些情况下，MSE可能不是最鲁棒的损失函数选择。例如，在数据分布不平衡或存在噪声的情况下，MSE可能会受到较大影响。

为了克服这些局限性，有时可以使用其他损失函数，如平均绝对误差（Mean Absolute Error，MAE）或Huber损失等。这些损失函数在某些方面比MSE更加鲁棒和灵活。

2. 均方根误差（Root Mean Squared Error，RMSE）

均方根误差（Root Mean Squared Error，RMSE）是机器学习和统计学中常用的误差度量指标，用于评估预测值与真实值之间的差异。

（1）RMSE的定义与公式

RMSE是通过计算预测值与实际值之间差的平方的平均值的平方根来衡量的。是MSE的平方根，与MSE有相同的量纲，其数学表达式为：

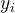
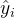
其中：是样本数量， $y_{i}$ 是第个样本的实际值（真实标签）。 $\hat{y}_{i}$ 是第个样本的预测值（模型输出）。

（2）RMSE的特点与应用

量纲一致性：由于RMSE是MSE的平方根，因此它的单位与原始数据的单位相同，这使得结果更易于理解和解释。
敏感性：RMSE对大误差更加敏感，因为平方运算会放大较大的误差值。这有助于模型在训练过程中更加关注那些预测错误较大的样本，从而提高模型的预测精度。
广泛应用：RMSE广泛应用于各种回归任务中，如房价预测、股票价格预测、销量预测等。在这些任务中，模型的目标是尽可能准确地预测连续变量的值，而RMSE则提供了一个衡量模型预测精度的有效指标。

（3）与其他误差度量指标的比较

平均绝对误差（MAE）：MAE计算的是预测值与实际值之间差的绝对值的平均值。与RMSE相比，MAE对异常值的敏感性较低，因为它不会放大较大的误差值。然而，MAE在计算过程中没有考虑到误差的方向，因此可能无法完全反映模型的预测性能。
平均绝对百分比误差（MAPE）：MAPE是预测误差与实际值之比的绝对值的平均值，通常以百分比形式表示。它对于不同量级的预测问题更具可比性。然而，当实际值接近零时，MAPE的计算可能会出现分母为零的情况，导致评价结果不可用。

（4）RMSE使用注意事项

异常值的影响：由于RMSE对大误差更加敏感，因此在含有较多异常值的数据集中，RMSE可能会偏高。为了降低异常值对RMSE的影响，可以考虑对数据进行预处理，如去除异常值或使用鲁棒的损失函数。
模型选择：在选择模型时，除了考虑RMSE外，还需要结合其他评估指标和实际需求进行综合判断。例如，在某些情况下，可能更关注模型的稳定性或解释性，而不仅仅是预测精度。

3. 平均绝对误差（Mean Absolute Error，MAE）

平均绝对误差（Mean Absolute Error，MAE）是一种常用的误差度量方式，主要用于回归任务，计算预测值与实际值之间差的绝对值的平均值。它对大误差和小误差的惩罚是相同的，因此不会过于敏感于极端值。

（1）MAE的定义与公式

MAE衡量的是预测值与实际值之间的平均绝对差距。其数学表达式为：

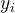
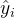
其中：是样本数量， $y_{i}$ 是第个样本的实际值（真实标签）。 $\hat{y}_{i}$ 是第个样本的预测值（模型输出）。||表示绝对值运算。

（2）MAE的特点

稳定性：由于MAE使用的是绝对值，因此它不会因为异常值（极端值）而受到过大影响，这一点比均方误差（MSE）更有优势。在数据中存在异常值时，MAE能提供更稳定的评估结果。
直观性：MAE是一个直观且易于理解的指标，能够直接反映预测值与实际值之间的平均差距。其单位与原数据的单位相同，这使得它具有更好的解释性。
鲁棒性：MAE对异常值的鲁棒性较好，因此在数据分布不平衡或存在噪声的情况下，MAE可能是一个更好的选择。

（3）MAE的应用

MAE通常用于评估模型在预测连续值时的性能，例如在天气预报、股票价格预测等领域。在这些任务中，模型的目标是尽可能准确地预测连续变量的值，而MAE则提供了一个衡量模型预测精度的有效指标。

（4）与其他误差度量指标的比较

均方误差（MSE）：MSE计算的是预测值与实际值之间差的平方的平均值。与MAE相比，MSE对大误差的惩罚更重（因为平方会放大误差），因此对异常值更敏感。在数据分布较为均匀且没有异常值的情况下，MSE可能是一个更好的选择。
均方根误差（RMSE）：RMSE是MSE的平方根，具有与原数据相同的量纲。与MSE类似，RMSE也对大误差更敏感，并且更容易受到异常值的影响。

（5）MAE的注意事项

数据预处理：在计算MAE之前，需要对数据进行适当的预处理，包括处理缺失值、异常值以及进行必要的转换。这有助于确保评估结果的准确性和可靠性。
模型选择：在选择模型时，除了考虑MAE外，还需要结合其他评估指标和实际需求进行综合判断。例如，在某些情况下，可能更关注模型的稳定性或解释性，而不仅仅是预测精度。

综上所述，平均绝对误差（MAE）是一种简单、直观且对异常值较为稳定的误差度量方法。它适合用于需要估计预测与真实值间差距的应用场景，特别是在数据中存在异常值时。

（二）分类任务

1. 交叉熵损失（Cross-Entropy Loss）

交叉熵损失（Cross-Entropy Loss）是机器学习和深度学习中常用的损失函数之一，尤其在分类问题中表现优异，特别是多分类任务。它衡量了两个概率分布之间的差异，即模型预测的分布和真实标签的分布。

（1）定义与公式

在分类问题中，模型会输出一个概率分布，表示样本属于各个类别的概率，而交叉熵损失则通过比较这个预测分布与真实分布来计算损失。

对于二分类问题，交叉熵损失的公式为：

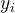
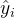
其中：是样本数量， $y_{i}$ 是第个样本的真实标签（0或1）。 $\hat{y}_{i}$ 是第个样本的预测概率。

对于多分类问题，交叉熵损失的公式可以推广为：

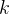
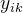
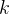
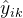
其中：是类别数量。 $y_{ik}$ 表示第个样本是否属于第个类别（0或1）。 $\hat{y}_{ik}$ 表示第个样本属于第个类别的预测概率。

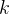
（2）特点与应用

计算简单且直观：交叉熵损失的计算方法相对简单，可以直接通过标准的数学库实现。同时，其直观性使得我们能够轻松理解模型预测与真实情况之间的差异。

良好的数学性质：交叉熵损失函数具有良好的数学性质，如凸性和可导性。这些性质有助于保证优化过程的稳定性和有效性。

适合处理多类别问题：交叉熵损失函数能够很好地处理多类别分类问题，通过分别计算每个类别的损失并求和来得到总损失。

快速收敛：与某些其他损失函数相比，交叉熵损失函数在反向传播过程中能够更快地收敛到最优解。这是因为其梯度与预测值和真实值之间的差异成正比，从而避免了梯度消失或爆炸的问题。

交叉熵损失在图像分类、文本分类、情感分析等任务中发挥着重要作用。在这些任务中，模型的目标是准确预测样本所属的类别，而交叉熵损失则提供了一个衡量模型预测精度的有效指标。

（3）优缺点

优点：对概率预测结果敏感，可以有效地优化模型。适用于二分类和多分类问题。计算简单且直观。

缺点：

对不平衡数据敏感：当数据集存在类别不平衡问题时，交叉熵损失函数可能会过度关注多数类而忽略了少数类。这可能导致模型在少数类上的性能不佳。为了克服这一缺点，可以采用加权交叉熵损失函数等方法。
计算量大：对于大型数据集，交叉熵损失函数的计算量可能较大，需要较长的训练时间。然而，随着计算能力的提升和算法的优化，这一问题正在逐渐得到解决。

（4）注意事项

数据预处理：在计算交叉熵损失之前，需要对数据进行适当的预处理，包括处理缺失值、异常值以及进行必要的转换（如one-hot编码等）。这有助于确保评估结果的准确性和可靠性。
模型选择：在选择模型时，除了考虑交叉熵损失外，还需要结合其他评估指标和实际需求进行综合判断。例如，在某些情况下，可能更关注模型的稳定性或解释性，而不仅仅是预测精度。
超参数调整：在使用交叉熵损失时，可能需要调整一些超参数（如学习率、批量大小等）以优化模型的性能。这些超参数的选择应根据具体任务和数据集的特点进行。

2. 负对数似然损失（Negative Log Likelihood Loss，NLL Loss）

负对数似然损失（Negative Log Likelihood Loss，NLL Loss）特别是在分类问题中常用的损失函数，特别是当模型输出是概率分布时。它计算了模型预测的概率分布与实际标签的概率分布之间的对数差异。

（1）NLL Loss的定义与公式

NLL Loss衡量的是模型预测的概率分布与真实概率分布之间的差异，通过计算对数概率的负值来实现。其数学表达式通常与具体的模型输出和标签形式有关，但一般形式可以表示为：

其中：是样本数量。 $p_{i,y_{i}}$ 表示第个样本真实类别 $y_{i}$ 对应的预测概率。

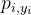
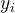
在PyTorch等深度学习框架中，NLL Loss通常与log_softmax激活函数一起使用，以避免数值计算时的上溢或下溢问题，并提高计算效率。具体地，模型首先输出未归一化的分数（logits），然后通过log_softmax将其转换为对数概率，最后使用NLL Loss计算损失。

（2）NLL Loss的特点与应用

适用于多分类问题：NLL Loss特别适用于具有多个类别的分类问题，如图像分类、文本分类等。
与交叉熵损失的关系：在多分类问题中，当标签采用独热编码时，交叉熵损失与NLL Loss在数学上是等价的。这意味着在实际应用中，可以互换使用这两种损失函数而不影响模型性能。然而，从输入形式上看，交叉熵损失（CrossEntropyLoss）通常直接接受模型的原始输出（logits）和真实标签，而NLL Loss则需要先通过log_softmax将原始输出转换为对数概率。
对概率预测敏感：NLL Loss对模型预测的概率值非常敏感，能够准确地反映模型预测与真实情况之间的差异。

（3）优缺点

优点：在多分类任务中表现优秀，数学上严谨。与交叉熵损失等价（在特定条件下），可以互换使用。

缺点：对于不平衡数据集可能表现不佳，因为NLL Loss会平等地对待所有样本，而不考虑它们的类别分布。在某些极端情况下可能不稳定，特别是当模型预测的概率值非常接近0或1时，对数运算可能会导致数值不稳定。

（4）注意事项

数据预处理：在计算NLL Loss之前，需要对数据进行适当的预处理，包括处理缺失值、异常值以及进行必要的转换（如标签的独热编码等）。
模型选择：在选择模型时，除了考虑NLL Loss外，还需要结合其他评估指标和实际需求进行综合判断。例如，在处理不平衡数据集时，可能需要考虑对损失函数进行加权或调整以改善模型性能。
超参数调整：在使用NLL Loss时，可能需要调整一些超参数（如学习率、批量大小等）以优化模型的性能。这些超参数的选择应根据具体任务和数据集的特点进行。

3. 自定义损失函数

根据特定任务的需求，可以设计自定义的损失函数。例如，在某些应用中，可能需要更关注于某些特定类型的误差或引入额外的约束条件。

三、损失函数的作用

1. 模型评估：损失函数提供了评估模型性能的方法。通过比较不同模型的损失值，我们可以选择性能最佳的模型。

2. 参数优化：在训练过程中，损失函数用于指导参数的更新。通过反向传播算法，我们可以计算出损失函数关于模型参数的梯度，并使用优化算法（如梯度下降）来更新参数，从而最小化损失函数。

3. 正则化：有时，我们会在损失函数中加入正则化项（如L1正则化或L2正则化），以防止模型过拟合。正则化项通过惩罚模型参数的复杂度来限制模型的复杂度，从而提高模型的泛化能力。

四、损失函数的选择

选择合适的损失函数对于模型的性能至关重要。在选择损失函数时，我们需要考虑以下因素：

任务类型：回归任务通常使用MSE或MAE等损失函数，而分类任务则使用交叉熵损失等。
数据分布：如果数据中存在异常值或极端值，可能需要选择对异常值不太敏感的损失函数（如MAE）。
模型特性：某些模型（如生成对抗网络GAN）可能需要使用特定的损失函数（如判别器损失和生成器损失）。
计算效率：某些损失函数的计算可能更加复杂或耗时，因此在实际应用中需要考虑计算效率的问题。