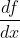矩阵求导的理解路径

摘要：整理矩阵求导的思路，便于后面复习快速回忆。

1 基础

函数表达式：y=f(x)

导数表达式： $\frac{df}{dx}$

熟悉高数的函数求导即可：

1）导数形式：加减乘除幂指对，三角反三角等，2）运算法则：交换律、分配率等。

元素对元素

即输出y的每一个元素对输入x的每一个元素。

如果f是标量，x是n维向量，则求导结果有1xn个元素

如果f是m维向量,x是n维向量，则对到结果是mxn个元素

如果f是qp矩阵，x是mn矩阵，则求导结果有qpmn个元素。

具体shape和布局有关。

分子：df(也即y)，分母：dx

分子布局

df的形式是列向量，包括标量,列向量f，行向量的转置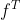 f^T ,等，都算列向量。

此时dx的形式是行向量。

分母布局

dx的形式是列向量，包括标量x,列向量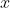，行向量的转置 x^T ,等，都算列向量。

此时df的形式是行向量。

能不能分子分母都是列向量和行向量？不行，前面说了，求导本质是df和dx两个要素的元素对元素，因此必然是一个要素横向按行展开，一个要素纵向按列展开。进一步假设，如果是三个要素，应该是三个方向展开。

布局选择

有雅克比和梯度形式，因为是考虑深度学习，就选择梯度形式：

df横向扩展

dx纵向扩展

1）将函数f化解成标量的元素表示，

2）标量元素求导

3）整理成原矩阵形式