最近想要总结一下 LTR的算法。
先讲解LTR的评价指标
排序指标
信息检索和推荐系统常用排序质量评分有4种:
- MRR(Mean Reciprocal Rank):平均倒数排名。 通用的对搜索推荐算法进行评价的机制,即第一个结果匹配,分数为1,第二个匹配分数为0.5,第n个匹配分数为1/n,如果没有匹配的句子分数为0。最终的分数为所有得分之和。
- MAP(Mean Average Precision):平均正确率均值。
- ERR(Expected Reciprocal Rank):预期倒数排名。
- NDCG(Normalized Discounted Cumulative Gain) :归一化折损累积增益。(DCG,IDCG,NDCG)
- AUC(Area under ROC Curve): ROC 曲线下的面积。
其中MRR和MAP 只能针对二级的相关性(排序等级:相关和不相关,也就是label只有0和1)进行评分,而NDCG和ERR则可以对多级的相关性进行评分(label可以为1,2,3,4,5 五个等级)。NDCG和ERR的另外一个优点是更关注排名靠前的文档,在计算分数时会给予排名靠前的文档更高的权重。但是这两种评分方式的缺点时函数不连续,不能进行求导,所以也就不能简单地将这两种评分方式加入到模型的损失函数中去。
1.1 MRR
对于一个查询
i
i
i 来说,
r
a
n
k
i
rank_i
ranki表示第一个相关结果的排序位置,所以
M
R
R
(
Q
)
=
1
∣
Q
∣
∑
i
=
1
∣
Q
∣
1
r
a
n
k
i
MRR(Q) = \frac{1}{|Q|}\sum^{|Q|}_{i=1}\frac{1}{rank_i}
MRR(Q)=∣Q∣1i=1∑∣Q∣ranki1
∣
Q
∣
|Q|
∣Q∣表示查询的数量,MRR表示搜索系统在查询集Q下的平均倒数排名值。MRR只能度量检索结果只有一个并且相关性等级只有相关和不相关两种的情况。
比如:
| 查询语句 | 查询结果 | 正确结果 | 排序位置 | 排序倒数 |
|---|---|---|---|---|
| 眼霜 | 小棕瓶精华,小棕瓶眼霜,面霜 | 小棕瓶眼霜 | 2 | 1/2 |
| 神仙水 | skII 神仙水,兰蔻粉水, 菌菇水 | skii神仙水 | 1 | 1 |
| 面膜 | 芦荟霜,高保湿面霜,skii面膜 | skii面膜 | 3 | 1/3 |
M R R ( Q ) = 1 / 2 + 1 / 3 + 1 3 = 11 18 MRR(Q) =\frac{1/2+1/3+1}{3} = \frac {11}{18} MRR(Q)=31/2+1/3+1=1811
1.2 MAP
假定信息需求
q
j
∈
Q
q_j \in Q
qj∈Q 对应的所有相关文档集合为
d
1
,
d
2
.
.
.
.
d
m
j
,
R
j
k
d_1, d_2....d_{mj}, R_{jk}
d1,d2....dmj,Rjk是返回结果中直到遇到
d
k
d_k
dk后其所在位置前(含
d
k
d_k
dk)的所有文档的集合,则定义
M
A
P
(
Q
)
2
MAP(Q)^2
MAP(Q)2如下:
M
A
P
(
Q
)
=
1
∣
Q
∣
∑
j
=
1
∣
Q
∣
1
m
j
∑
k
=
1
m
j
P
r
e
c
i
s
i
o
n
(
R
j
k
)
MAP(Q) = \frac {1}{|Q|}\sum^{|Q|}_{j=1}\frac{1}{m_j}\sum_{k=1}^{m_j}Precision(R_{jk})
MAP(Q)=∣Q∣1j=1∑∣Q∣mj1k=1∑mjPrecision(Rjk)
∣
Q
∣
|Q|
∣Q∣表示查询的数量.
其实有两种计算MPP的方法:
- 第一种,是在每篇相关文档所在位置上求正确率然后平均. 这个称为 非插值MAP(Q), 一般的MAP就是指这个。
- 另一种,是在每个召回率水平上计算此时的插值正确率,然后求平均正确率,最后在不同查询之间计算均值。
| 查询1 MAC 口红 | – | 查询2 神仙水 | – |
|---|---|---|---|
| 排序位置 | 是否相关 | 排序位置 | 是否相关 |
| 1 | 是 | 1 | 否 |
| 2 | 是 | 2 | 是 |
| 3 | 否 | 3 | 是 |
| 4 | 否 | 4 | 否 |
| 5 | 是 | 5 | 否 |
| 6 | 否 | 6 | 是 |
| 7 | 否 | 7 | 是 |
针对上面的检索结果,可以计算出:
A
P
(
1
)
=
(
1
∗
1
+
1
∗
1
+
2
/
3
∗
0
+
2
/
4
∗
0
+
3
/
5
∗
1
+
3
/
6
∗
0
+
3
/
7
∗
0
)
/
3
=
13
/
15
AP(1) = (1*1 + 1*1 + 2/3*0 + 2/4*0 + 3/5*1 + 3/6*0 + 3/7*0)/3=13/15
AP(1)=(1∗1+1∗1+2/3∗0+2/4∗0+3/5∗1+3/6∗0+3/7∗0)/3=13/15
A
P
(
2
)
=
(
0
∗
0
+
1
/
2
∗
1
+
2
/
3
∗
1
+
2
/
4
∗
0
+
2
/
5
∗
0
+
3
/
6
∗
1
+
4
/
7
∗
1
)
/
4
=
47
/
84
AP(2) = (0*0 + 1/2*1 + 2/3*1 + 2/4*0 + 2/5*0+3/6*1+4/7*1)/4 = 47/84
AP(2)=(0∗0+1/2∗1+2/3∗1+2/4∗0+2/5∗0+3/6∗1+4/7∗1)/4=47/84
M
A
P
(
Q
)
=
A
P
(
1
)
+
A
P
(
2
)
2
=
13
/
15
+
47
/
84
2
=
599
420
MAP(Q) = \frac{AP(1) + AP(2)}{2} = \frac{13/15 + 47/84}{2} = \frac{599}{420}
MAP(Q)=2AP(1)+AP(2)=213/15+47/84=420599
1.3 NDCG
NDCG是基于前k个检索结果进行计算的,推荐系统通常为某个用户的一次搜索返回一个item列表,加上长度为K, 这时用NDCG@K评价该排序列表与用户真实交互列表的差距。
NDCG: Normalized Discounted Cumulative Gain.
- Gain: 表示列表中每一个item的相关性分数。$Gain = r(i) $
- Cumulative Gain:表示对K个item的Gain的累加。 C G @ K = ∑ i K r ( i ) CG@K =\sum_i^Kr(i) CG@K=∑iKr(i)
- Discounted Cumulative Gain: 考虑排序顺序的因素,使得排名考前的item的增益更高,对排名靠后的item进行折损。 D C G @ K = ∑ i K 2 r ( i ) l o g ( 1 + i ) DCG@K = \sum_i^K\frac{2^{r(i)}}{log(1+i)} DCG@K=∑iKlog(1+i)2r(i)
- Normalized Discounted Cumulative Gain: DCG 能够对一个用户的推荐列表进行评价,如果用该指标评价某个推荐算法,需要对所有用户的推荐列表进行评价,而不同用户之间的DCG相比没有意义(不同用户的兴趣不同,对同样的item排名前后不同)。所以要对每次搜索的指标进行归一化,于是就对每次搜索计算一个理想情况下的DCG分数,用IDCG来表示。然后用每次搜索的DCG与IDCG之比作为归一化后的分值,最后对每次搜索取平均得到最终的分值,NDCG。
设R(j, m)是评价人员给出的文档
d
d
d对查询
j
j
j的相关性得分,那么有:
N
D
C
G
(
Q
,
k
)
=
1
∣
Q
∣
∑
j
=
1
∣
Q
∣
D
C
G
k
I
D
C
G
k
=
1
∣
Q
∣
∑
j
=
1
∣
Q
∣
Z
j
,
k
∑
m
=
1
k
2
R
(
j
,
m
)
−
1
l
o
g
(
1
+
m
)
NDCG(Q,k) = \frac {1}{|Q|}\sum_{j=1}^{|Q|}\frac{DCG_k}{IDCG_k}= \frac{1}{|Q|}\sum_{j=1}^{|Q|}Z_{j,k}\sum_{m=1}^{k}\frac{2^{R(j,m)}-1}{log(1+m)}
NDCG(Q,k)=∣Q∣1j=1∑∣Q∣IDCGkDCGk=∣Q∣1j=1∑∣Q∣Zj,km=1∑klog(1+m)2R(j,m)−1,其中
D
C
G
k
=
∑
m
=
1
k
2
R
(
j
,
m
)
−
1
l
o
g
(
1
+
m
)
DCG_{k} = \sum_{m=1}^{k}\frac{2^{R(j,m)}-1}{log(1+m)}
DCGk=m=1∑klog(1+m)2R(j,m)−1
∣
Q
∣
|Q|
∣Q∣表示查询的数量.
Z
j
,
k
Z_{j,k}
Zj,k为第
j
j
j个查询的DCG归一化因子,用于保证对于查询
j
j
j最完美系统的
D
C
G
k
DCG_k
DCGk得分是1.
Z
j
.
k
Z_{j.k}
Zj.k也可以用
1
I
D
C
G
k
\frac{1}{IDCG_k}
IDCGk1表示。m是返回文档的位置。如果某查询返回的文档数
k
′
<
k
k' < k
k′<k, 那么上述公式只需计算到
k
′
k'
k′为止。
这里解释一下DCG和IDCG:
| 查询1:MAC口红 | 查询2:神仙水 | ||
|---|---|---|---|
| 排序位置 | 相关程度 | 排序位置 | 相关程度 |
| 1 | 3 | 1 | 2 |
| 2 | 2 | 2 | 2 |
| 3 | 3 | 3 | 3 |
| 4 | 0 | 4 | 1 |
| 5 | 1 | 5 | 2 |
| 6 | 2 | 6 | 3 |
| 7 | 2 | 7 | 1 |
对于查询1:MAC口红:
D
C
G
7
=
∑
m
=
1
7
2
R
(
j
,
m
)
−
1
l
o
g
(
1
+
m
)
=
21.421516
DCG_7 = \sum_{m=1}^{7}\frac{2^{R(j,m)} - 1}{log(1+m)} = 21.421516
DCG7=m=1∑7log(1+m)2R(j,m)−1=21.421516
查询1返回结果的最佳相关程度排序为3,3,2,2,2,1,0. 所以,IDCG7 = 22.686817,
N
D
C
G
7
=
D
C
G
7
I
D
C
G
7
=
0.944227
NDCG_7 = \frac{DCG_7}{IDCG_7} = 0.944227
NDCG7=IDCG7DCG7=0.944227
对于查询2:神仙水:
D
C
G
7
=
∑
m
=
1
7
2
R
(
j
,
m
)
−
1
l
o
g
(
1
+
m
)
=
18.482089
DCG_7 = \sum_{m=1}^{7}\frac{2^{R(j,m)} - 1}{log(1+m)} = 18.482089
DCG7=m=1∑7log(1+m)2R(j,m)−1=18.482089
查询2返回结果的最佳相关程度排序为3,3,2,2,2,1,1. 所以,IDCG7 = 23.167716,
N
D
C
G
7
=
D
C
G
7
I
D
C
G
7
=
0.797752
NDCG_7 = \frac{DCG_7}{IDCG_7} = 0.797752
NDCG7=IDCG7DCG7=0.797752
最后可得:
N
D
C
G
(
Q
,
7
)
=
(
0.944227
+
0.797752
)
/
2
=
0.870990
NDCG(Q,7) = (0.944227 + 0.797752)/2 = 0.870990
NDCG(Q,7)=(0.944227+0.797752)/2=0.870990
1.4 ERR
ERR 旨在改善NDCG计算当前结果时未考虑排在前面结果的影响的缺点,提出了一种基于级联模型的评价指标。首先定义:
R
(
g
)
=
2
g
−
1
2
g
m
a
x
,
g
∈
0
,
1
,
.
.
.
.
g
m
a
x
R(g) = \frac{2^g-1}{2^{g_{max}}},g\in{0,1,....g_{max}}
R(g)=2gmax2g−1,g∈0,1,....gmax
g代表文档的得分级别,
g
m
a
x
g_{max}
gmax代表最大的分数级别。
于是定义
E
R
R
=
∑
r
=
1
n
1
r
∏
i
=
1
r
−
1
(
1
−
R
i
)
R
r
ERR = \sum_{r=1}^n \frac{1}{r}\prod_{i=1}^{r-1}(1-R_i)R_r
ERR=r=1∑nr1i=1∏r−1(1−Ri)Rr
展开公式如下:
E
R
R
=
R
1
+
1
2
(
1
−
R
1
)
R
2
+
1
3
(
1
−
R
1
)
(
1
−
R
2
)
R
3
+
.
.
.
1
n
(
1
−
R
1
)
(
1
−
R
2
)
.
.
(
1
−
R
n
−
1
)
R
n
ERR = R_1 + \frac{1}{2}(1-R_1)R_2 + \frac{1}{3}(1-R_1)(1-R_2)R_3 + ... \frac{1}{n}(1-R_1)(1-R_2)..(1-R_{n-1})R_n
ERR=R1+21(1−R1)R2+31(1−R1)(1−R2)R3+...n1(1−R1)(1−R2)..(1−Rn−1)Rn
举例来说:
g_max = 3
| 查询 口红 | |
|---|---|
| 排序位置 | 相关程度 |
| 1 | 3 |
| 2 | 2 |
| 3 | 3 |
| 4 | 1 |
R
1
=
0.875
,
R
2
=
0.375
,
R
3
=
0.875
,
R
4
=
0.125
R_1 = 0.875, R_2 = 0.375, R_3=0.875, R_4=0.125
R1=0.875,R2=0.375,R3=0.875,R4=0.125
E
R
R
=
0.875
+
1
2
∗
0.125
∗
0.375
+
1
3
∗
0.125
∗
0.625
∗
0.875
+
1
4
∗
0.125
∗
0.625
∗
0.125
∗
0.125
=
0.913391
ERR = 0.875 + \frac{1}{2}*0.125*0.375 + \frac{1}{3}*0.125*0.625*0.875 + \frac{1}{4} * 0.125*0.625*0.125*0.125=0.913391
ERR=0.875+21∗0.125∗0.375+31∗0.125∗0.625∗0.875+41∗0.125∗0.625∗0.125∗0.125=0.913391
1.5 AUC
可以参考如何理解机器学习和统计中的AUC
我们知道在分类问题中,可以用错误率error rate和 精度acc评估,有时候当我们不想关注整体的正确率或者错误率时,更关注某个类别的准确率时,可以用查准率precision和查全率recall来评估。
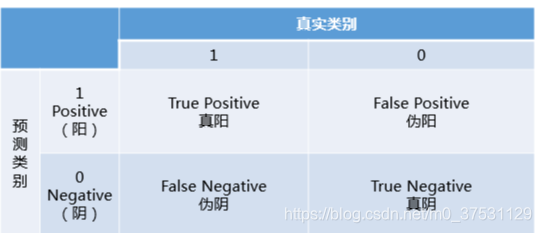
对于二分类问题,上面的acc, precision, recall, error rate 都需要理解清楚 下图的混淆矩阵。
-
预测类别: Positive (1 阳性), Negative(0,阴性)
-
真实类别:1 正类和 0 负类
-
预测正确为True, 预测错误为False.
-
True Positive: 将正类预测为正类。
-
True Negative: 将负类预测为负类。
-
False Positive: 将负类预测为正类。—误报。
-
False Negative:将正类预测为负类。—漏报。
-
查全率 p r e c i s i o n = T P T P + F P precision = \frac{TP}{TP+FP} precision=TP+FPTP
-
召回率(查准率) r e c a l l = T P T P + F N recall = \frac{TP}{TP+FN} recall=TP+FNTP
-
精度 A c c = T P + T N T P + F P + T N + F N Acc = \frac{TP+TN}{TP+FP+TN+FN} Acc=TP+FP+TN+FNTP+TN
查全率和查准率根据阈值不同,处于你进我退的平衡中,根据具体项目的需求进行权衡。将两者进行结合就得到了 F-score.
- Fscore F = 2 ∗ P r e c i s i o n ∗ R e c a l l P r e c i s i o n + R e c a l l F = \frac{2*Precision * Recall}{Precision+Recall} F=Precision+Recall2∗Precision∗Recall 也成为F1score. 它的一般形式定义为 F β = ( 1 + β 2 ) ( P r e c i s i o n + R e c a l l ) β 2 ∗ P r e c i s i o n + R e c a l l F_{\beta} = \frac{(1+\beta^2)(Precision+Recall)}{\beta^2 *Precision + Recall} Fβ=β2∗Precision+Recall(1+β2)(Precision+Recall)可以根据参数 β \beta β给与两者不同权重。
Precision和Recall和ACC有个缺陷就是当正负样本不平衡时,很难表征结果。比如广告点击率CTR一般都是千分之几,如果用acc表示,即使全部预测为负类(不点击)acc也是99%以上,没啥意义。
而从排序质量角度考虑这个问题则可以减小样本不平衡带来的问题,排序本身的质量好坏,体现了综合考虑模型在不同任务下的“期望泛化性能”的好坏,ROC 曲线则是从这个角度出发的。ROC 曲线的纵轴是“真正例率”(TPR),横轴是“假正例率”(FPR),两者定义分别为:
T
P
F
=
T
P
T
P
+
F
N
,
F
P
R
=
F
P
T
N
+
F
P
TPF = \frac{TP}{TP+FN}, FPR = \frac{FP}{TN+FP}
TPF=TP+FNTP,FPR=TN+FPFP
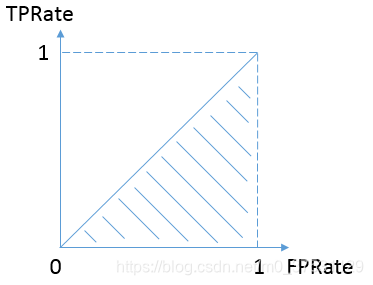
在现实任务中通常利用有限个测试样例绘制 ROC 曲线,仅凭 ROC 曲线不容易判定模型性能,较为合理的依据是比较 ROC 曲线下的面积,即 AUC(Area Under ROC Curve)。AUC 通过对 ROC 曲线下各部分的面积求和而得. ROC曲线的横轴是FPRate,纵轴是TPRate,当二者相等时,即y=x,如下图:
表示的意义是:对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的。换句话说,分类器对于正例和负例毫无区分能力,和抛硬币没什么区别,一个抛硬币的分类器是我们能想象的最差的情况,因此一般来说我们认为AUC的最小值为0.5(当然也存在预测相反这种极端的情况,AUC小于0.5,这种情况相当于分类器总是把对的说成错的,错的认为是对的,那么只要把预测类别取反,便得到了一个AUC大于0.5的分类器)。
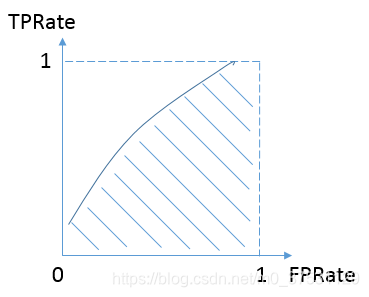
而我们希望分类器达到的效果是:对于真实类别为1的样本,分类器预测为1的概率(即TPRate),要大于真实类别为0而预测类别为1的概率(即FPRate),即y>x,因此大部分的ROC曲线长成下面这个样子:
最理想的情况下,既没有真实类别为1而错分为0的样本——TPRate一直为1,也没有真实类别为0而错分为1的样本——FP rate一直为0,AUC为1,这便是AUC的极大值。
AUC的计算方法同时考虑了分类器对于正例和负例的分类能力,在样本不平衡的情况下,依然能够对分类器作出合理的评价。
主要参考文献:
From RankNet to LambdaRank to LambdaMART:An Overview 中的第三部分 Information Retrieval Measure
A Short Introduction to Learning to Rank
知乎NDCG