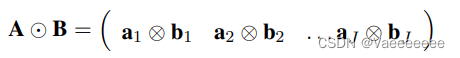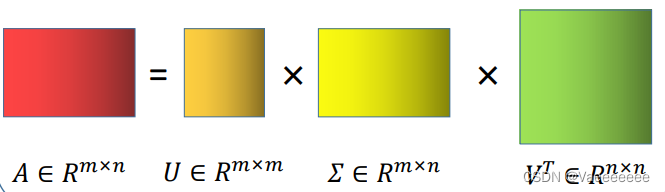文章目录
前言
本文主要详细介绍一些关于张量压缩感知方面的内容,包括相关的基础概念和一些算法原理,并给出具体的Python代码实现过程。
基本概念
1.1 什么是张量
用一张图可以很好的理解:
1.2 张量的“积”运算
1.2.1 张量内积
- 含义:两个相同阶的张量 A 、 B ∈ R I 1 × I 2 . . . × I N A、B ∈ R^{I_{1}×I_{2}...×I_{N}} A、B∈RI1×I2...×IN 之间的运算,是两个张量位置相对应的元素乘积之后的总和。
- 符号表示: < A ‾ , B ‾ > <\underline{A},\underline{B}> <A,B>
1.2.2 张量外积
- 含义:张量 A ∈ R I 1 × I 2 . . . × I N A ∈ R^{I_{1}×I_{2}...×I_{N}} A∈RI1×I2...×IN和张量 B ∈ R J 1 × J 2 . . . × J M B ∈ R^{J_{1}×J_{2}...×J_{M}} B∈RJ1×J2...×JM 的外积是对应的向量元素的乘积。
- 符号表示:
A
A
A
∘
\circ
∘
B
B
B
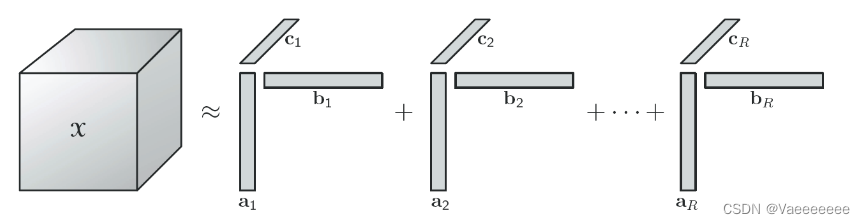
秩1张量:若某个张量 X X X可以表示为 n n n个向量的外积时,则 X X X的秩为1。例如下图中的两个张量,都是秩1张量。
1.2.3 kronecker积
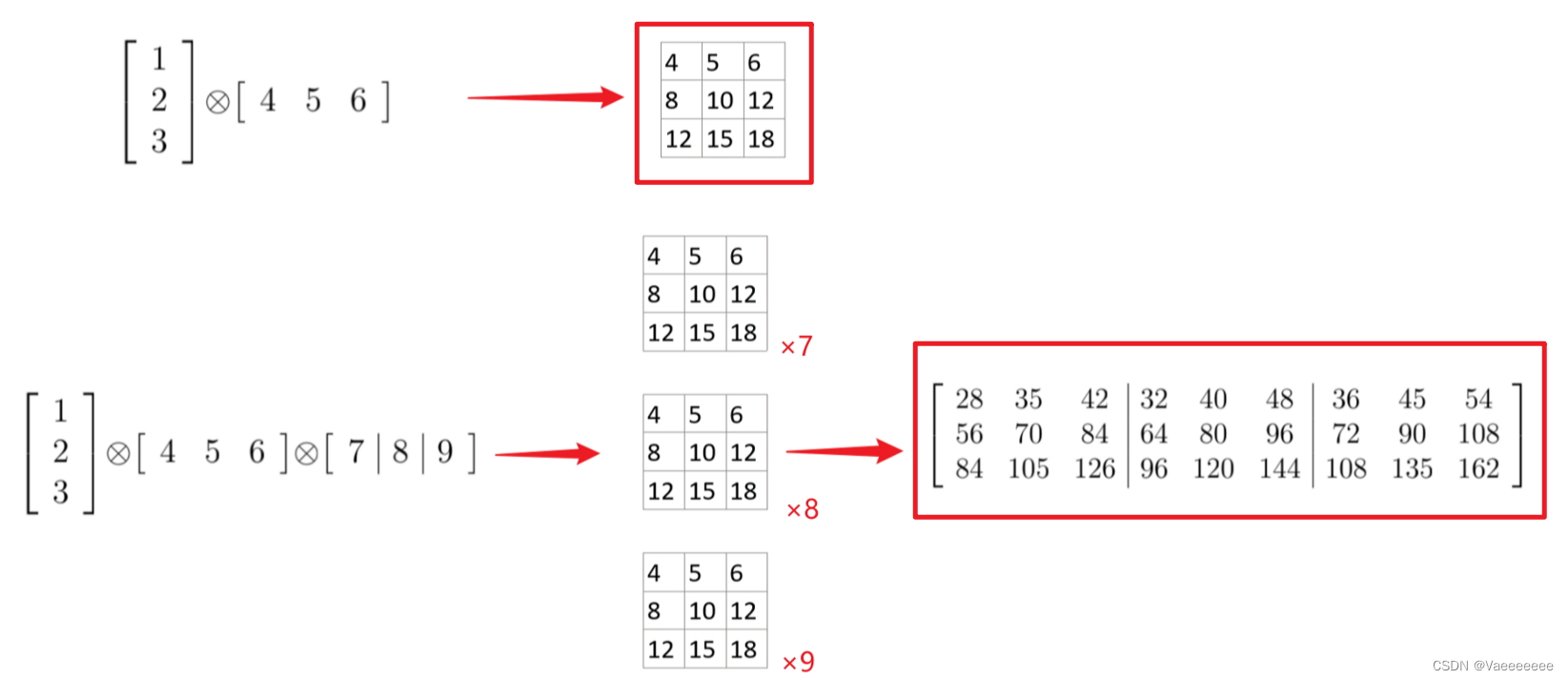
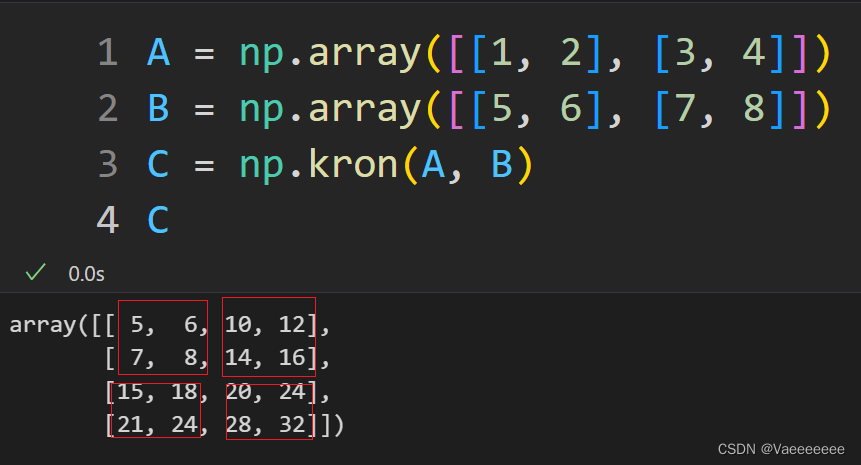
- 含义:设 A ∈ R m × n A∈ R^{m×n} A∈Rm×n 和 B ∈ R p × q B∈R^{p×q} B∈Rp×q 是两个矩阵,则它们之间的 K r o n e c k e r Kronecker Kronecker 积是 A A A 中的每个元素分别与矩阵 B B B 相乘得到一个 ( m p ) × ( n q ) (mp)×(nq) (mp)×(nq)大小的矩阵,其定义如下:
A ⊗ B = ( a 11 B a 12 B ⋯ a 1 n A B a 21 B a 22 B ⋯ a 2 n A B ⋮ ⋮ ⋱ ⋮ a m A 1 B a m A 2 B ⋯ a m A n A B ) = ( a 11 b 11 a 11 b 12 ⋯ a 11 b 1 n B ⋯ a 1 n A b 11 a 1 n A b 12 ⋯ a 1 n A b 1 n B a 11 b 21 a 11 b 22 ⋯ a 11 b 2 n B ⋯ a 1 n A b 21 a 1 n A b 22 ⋯ a 1 n A b 2 n B ⋮ ⋮ ⋱ ⋮ ⋱ ⋮ ⋮ ⋱ ⋮ a m A 1 b 11 a m A 1 b 12 ⋯ a m A 1 b 1 n B ⋯ a m A n A b 11 a m A n A b 12 ⋯ a m A n A b 1 n B ) \begin{aligned} A\otimes B &=\begin{pmatrix}a_{11}B&a_{12}B&\cdots&a_{1n_A}B\\a_{21}B&a_{22}B&\cdots&a_{2n_A}B\\\vdots&\vdots&\ddots&\vdots\\a_{m_A1}B&a_{m_A2}B&\cdots&a_{m_An_A}B\end{pmatrix} \\ &= \begin{pmatrix}a_{11}b_{11} & a_{11}b_{12} & \cdots & a_{11}b_{1n_B} & \cdots & a_{1n_A}b_{11} & a_{1n_A}b_{12} & \cdots & a_{1n_A}b_{1n_B} \\a_{11}b_{21} & a_{11}b_{22} & \cdots & a_{11}b_{2n_B} & \cdots & a_{1n_A}b_{21} & a_{1n_A}b_{22} & \cdots & a_{1n_A}b_{2n_B}\\\vdots & \vdots & \ddots & \vdots & \ddots & \vdots &\vdots & \ddots & \vdots\\a_{m_A1}b_{11} & a_{m_A1}b_{12} & \cdots & a_{m_A1}b_{1n_B} & \cdots & a_{m_An_A}b_{11} & a_{m_An_A}b_{12} & \cdots & a_{m_An_A}b_{1n_B} \end{pmatrix} \end{aligned} A⊗B= a11Ba21B⋮amA1Ba12Ba22B⋮amA2B⋯⋯⋱⋯a1nABa2nAB⋮amAnAB = a11b11a11b21⋮amA1b11a11b12a11b22⋮amA1b12⋯⋯⋱⋯a11b1nBa11b2nB⋮amA1b1nB⋯⋯⋱⋯a1nAb11a1nAb21⋮amAnAb11a1nAb12a1nAb22⋮amAnAb12⋯⋯⋱⋯a1nAb1nBa1nAb2nB⋮amAnAb1nB
其中, a i j a_{ij} aij 和 b k l b_{kl} bkl 分别代表矩阵 A A A 和 B B B 的元素, a i j B a_{ij}B aijB 代表矩阵 B B B 中的每个元素都乘以 a i j a_{ij} aij,得到的结果组合成逐元素乘积的矩阵。
- 符号表示: A A A ⊗ \otimes ⊗ B B B
1.2.4 Hadamard积
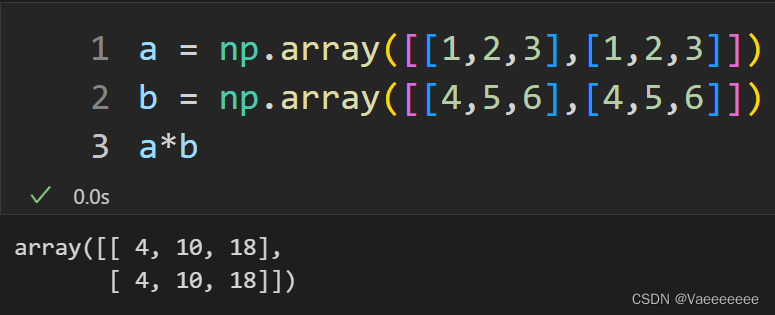
- 含义:就是两个矩阵对应元素相乘,即矩阵间的点乘,要求两个矩阵的大小相等。
符号表示: A A A ⊛ \circledast ⊛ B B B
1.2.5 Khatri-Rao积
- 含义:又称为列分解相乘(CP)积。
假设有两个矩阵 A m × r A_{m \times r} Am×r和 B n × r B_{n \times r} Bn×r,那么它们的 K h a t r i − R a o Khatri-Rao Khatri−Rao积所得的矩阵维数为 ( m n ) × r (mn)×r (mn)×r。换句话说矩阵的Khatri-Rao积就是两个矩阵对应列的Kronecker积。
- 符号表示: A A A ⊙ \odot ⊙ B B B
1.2.6 n模张量-矩阵积(模态积)
- 含义:设 N N N阶张量 X ∈ R I 1 × I 2 . . . × I N \mathcal{X} ∈ R^{I_{1}×I_{2}...×I_{N}} X∈RI1×I2...×IN 矩阵 U ∈ R J × I n U∈ R^{J×I_{n}} U∈RJ×In ,二者的 n n n模积得到的结果是一个 I 1 × . . . × I n − 1 × J × I n + 1 × . . . × I N I_{1}×...×I_{n-1}×J×I_{n+1}×...×I_{N} I1×...×In−1×J×In+1×...×IN的张量,即 I n I_{n} In维度大小变为 J J J。
- 符号表示 X × n U \mathcal{X} \times_{n}U X×nU
1.2.7 Numpy中的“积”运算
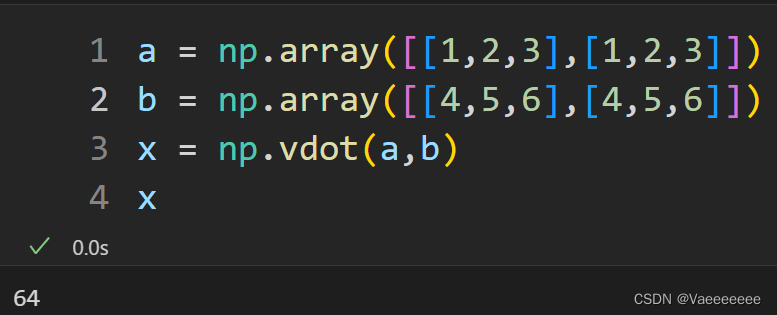
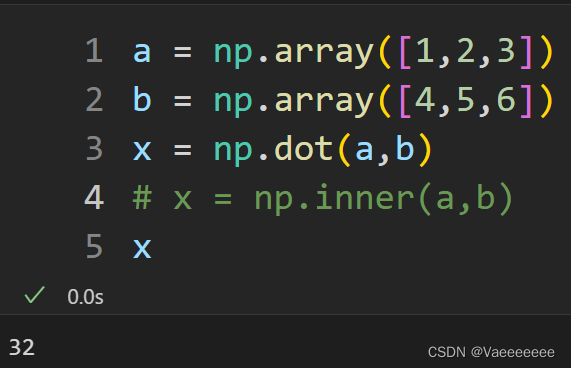
1.内积——np.vdot()函数
对于两个向量的内积,也可以使用np.inner()或者np.dot函数
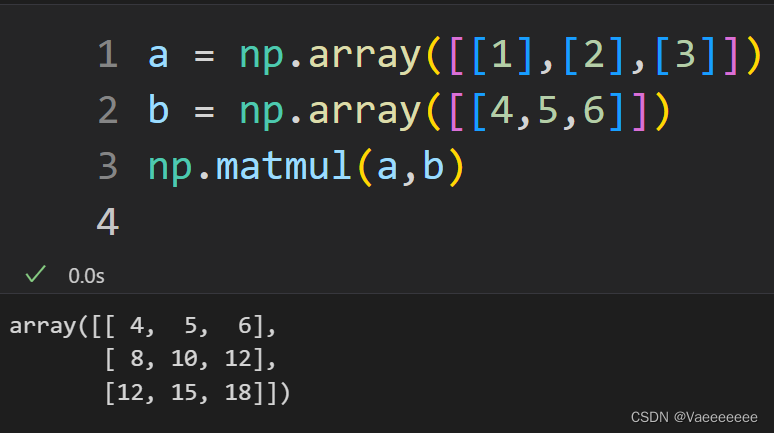
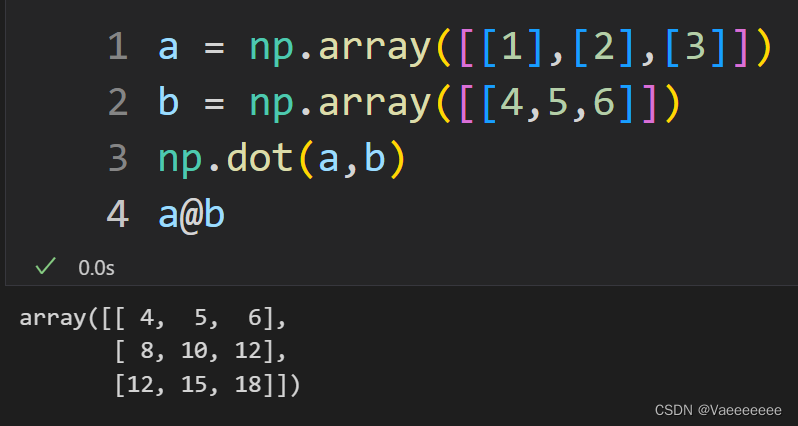
2.外积——np.matmul函数或者直接使用 @ 运算符
3.kronecker积——np.kron()
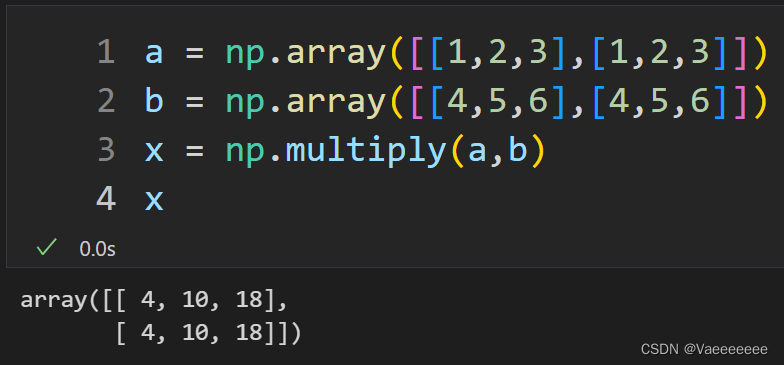
4.Hadamard积——np.multiply函数和 * 运算符
5.模态积——np.einsum()
假设三阶张量
X
i
×
j
×
k
\mathcal{X}^{i\times j\times k}
Xi×j×k,矩阵
U
a
×
b
U^{a\times b}
Ua×b,则
-
X
×
1
U
\mathcal{X} \times_{1}U
X×1U:
np.einsum('ijk,ab->ajk',X,U) -
X
×
2
U
\mathcal{X} \times_{2}U
X×2U:
np.einsum('ijk,ab->iak',X,U) -
X
×
3
U
\mathcal{X} \times_{3}U
X×3U:
np.einsum('ijk,ab->ija',X,U)
1.3 张量的分解运算
1.3.1CP分解
一种基于高阶张量的矩阵分解方法,简单点说就是将
N
N
N阶张量
X
∈
R
I
1
×
I
2
.
.
.
×
I
N
\mathcal{X} ∈ R^{I_{1}×I_{2}...×I_{N}}
X∈RI1×I2...×IN分解成多个形状相同的秩一张量的和。
数学表达:
X
≈
[
[
λ
;
A
(
1
)
,
A
(
2
)
,
⋅
⋅
⋅
A
(
N
)
]
]
≡
∑
s
=
1
R
λ
r
α
r
(
1
)
∘
α
r
(
2
)
∘
α
r
(
3
)
∘
⋅
⋅
⋅
α
r
(
n
)
(
1
)
数学表达:\mathcal{X} \approx[[ \lambda ;A^{(1)},A^{(2)},\cdot\cdot\cdot A^{(N)}]]\equiv\sum_{s=1}^{R}\lambda_{r}\alpha_{r}^{(1)}\circ\alpha_{r}^{(2)}\circ\alpha_{r}^{(3)}\circ\cdot\cdot\cdot\alpha_{r}^{(n)} \quad \quad (1)
数学表达:X≈[[λ;A(1),A(2),⋅⋅⋅A(N)]]≡s=1∑Rλrαr(1)∘αr(2)∘αr(3)∘⋅⋅⋅αr(n)(1)
λ
:为了将
A
(
1
)
−
A
(
N
)
中每列值归一化时,引入的参数列
\lambda:为了将A^{(1)}-A^{(N)}中每列值归一化时,引入的参数列
λ:为了将A(1)−A(N)中每列值归一化时,引入的参数列
R
:
C
P
秩
R:CP秩
R:CP秩
当
X
\mathcal{X}
X阶数为3时的分解示意图如下:
我们把通过外积组成秩1张量元素的向量集合为因子矩阵,例如令
A
=
[
a
1
a
2
.
.
.
a
R
]
A = [a_{1} a_{2}...a_{R}]
A=[a1a2...aR],
B
=
[
b
1
b
2
.
.
.
b
R
]
B = [b_{1} b_{2}...b_{R}]
B=[b1b2...bR],
C
=
[
c
1
c
2
.
.
.
c
R
]
C = [c_{1} c_{2}...c_{R}]
C=[c1c2...cR],不难发现因子矩阵存在一个共同点,那就是他们的列维度肯定是相同的。
- 上面
(
1
)
(1)
(1)式可用因子矩阵表示为
X ( 1 ) ≈ A ( C ⊙ B ) T \mathcal{X} _{(1) }\approx A(C\odot B) ^T X(1)≈A(C⊙B)T X ( 2 ) ≈ B ( C ⊙ A ) T \mathcal{X} _{(2) } \approx B(C\odot A) ^T X(2)≈B(C⊙A)T X ( 3 ) ≈ C ( B ⊙ A ) T \mathcal{X} _{(3) } \approx C (B\odot A) ^T \\ X(3)≈C(B⊙A)T
X ( n ) \mathcal{X} _{(n)} X(n):表示张量以第 n n n模态展开得到的矩阵。
1.3.1.1 CP分解算法——ALS-CP(交替最小二乘法)
现在已经知道分解的方法和原理,那么接下来的问题就是如何进行有效分解,其实就是寻找
R
R
R (
X
\mathcal{X}
X的CP秩) 个秩一向量使得其估计得到的张量最接近初始张量,即待优化的问题为:
m
i
n
∣
∣
X
~
−
X
∣
∣
min \mid\mid\widetilde{\mathcal{X} }-\mathcal{X} \mid\mid
min∣∣X
−X∣∣
而
A
L
S
ALS
ALS的思想很简单,以三阶张量分解为例,对应的因子矩阵为
A
、
B
、
C
A、B、C
A、B、C,算法流程为:
1.初始化:随机生成一个三维张量X和一个rank为R的分解矩阵集合{A,B,C}。
2.交替更新A、B、C三个矩阵:
a. 固定B和C,通过最小化目标函数来更新A矩阵。
b. 固定A和C,通过最小化目标函数来更新B矩阵。
c. 固定A和B,通过最小化目标函数来更新C矩阵。
3.重复步骤2直到收敛,即当目标函数达到一定精度或迭代次数达到一定值时停止。
4.输出分解矩阵集合{A,B,C},即为原始张量X的CP分解结果
其中,目标函数为:
m i n A , B , C ∑ i , j , k ( X i , j , k − ∑ r = 1 R A i , r B j , r C k , r ) 2 min_{A,B,C}\sum_{i,j,k}(X_{i,j,k} - \sum_{r=1}^{R}A_{i,r}B_{j,r}C_{k,r})^2 minA,B,Ci,j,k∑(Xi,j,k−r=1∑RAi,rBj,rCk,r)2
在每次更新A、B、C矩阵时,可以使用最小二乘法(Least squares)来求解目标函数的最小值,即:
- a. 对于A矩阵,固定B和C,最小化问题被写成:
min
A
^
∣
∣
X
(
1
)
−
A
^
(
C
⊙
B
)
T
∣
∣
F
\operatorname*{min}_{\hat{A}} ||\mathcal{X} _{(1)}-\hat{A} (C\odot B) ^T ||_{F}
A^min∣∣X(1)−A^(C⊙B)T∣∣F
故
A
^
\hat{A}
A^ 的最优解为:
A
^
=
X
(
1
)
[
(
C
⊙
B
)
T
]
†
(
2
)
†
:表示伪逆
\hat{A}=\mathcal{X} _{(1)}[(C\odot B) ^T]^{\dagger}\quad\quad(2) \\\dagger:表示伪逆
A^=X(1)[(C⊙B)T]†(2)†:表示伪逆
其中,上式又可以根据
K
h
a
t
r
i
−
R
a
o
Khatri-Rao
Khatri−Rao 积的性质写成:
A
^
=
X
(
1
)
(
C
⊙
B
)
(
C
T
C
∗
B
T
B
)
†
(
3
)
\hat{A}=\mathcal{X} _{(1)}(C\odot B)(C^{T}C * B^{T}B)^{\dagger}\quad\quad(3)
A^=X(1)(C⊙B)(CTC∗BTB)†(3)
注意:
(
3
)
(3)
(3)式相比
(
2
)
(2)
(2)式的优势在于可以降低计算伪逆矩阵时的计算量,但是会存在数值病态条件的可能。
- b. 类似地,对于B矩阵作同样操作:
B
^
\hat{B}
B^ 的最优解为:
B
^
=
X
(
2
)
[
(
C
⊙
A
)
T
]
†
\hat{B}=\mathcal{X} _{(2)}[(C\odot A) ^T]^{\dagger}\quad\quad
B^=X(2)[(C⊙A)T]†
或者
B
^
=
X
(
2
)
(
C
⊙
A
)
(
C
T
C
∗
A
T
A
)
†
\hat{B}=\mathcal{X} _{(2)}(C\odot A)(C^{T}C * A^{T}A)^{\dagger}\quad\quad
B^=X(2)(C⊙A)(CTC∗ATA)†
- c. C矩阵的更新公式:
C
^
\hat{C}
C^ 的最优解为:
C
^
=
X
(
3
)
[
(
B
⊙
A
)
T
]
†
\hat{C}=\mathcal{X} _{(3)}[(B\odot A) ^T]^{\dagger}\quad\quad
C^=X(3)[(B⊙A)T]†
或者
C
^
=
X
(
3
)
(
B
⊙
A
)
(
B
T
B
∗
A
T
A
)
†
\hat{C}=\mathcal{X} _{(3)}(B\odot A)(B^{T}B * A^{T}A)^{\dagger}\quad\quad
C^=X(3)(B⊙A)(BTB∗ATA)†
- 下面是具体实现代码:
import numpy as np
from numpy.linalg import norm
from scipy.linalg import khatri_rao
def tensor_mode_unfold(T, p): #函数功能:将张量tensor按模式p展开成矩阵
"""
Unfold tensor T along mode p
"""
T = np.moveaxis(T, p-1, 0)
new_shape = (T.shape[0], np.prod(T.shape[1:]))
T = np.reshape(T, new_shape)
return T
def als_cp(X, R, max_iter=100, tol=1e-6):
"""
ALS-CP算法对三维张量X进行CP分解
:param X: 三维张量
:param R: 分解矩阵集合{A,B,C}的rank
:param max_iter: 最大迭代次数
:param tol: 收敛精度
:return: 分解矩阵集合{A,B,C}
"""
#随机初始化A,B,C
n1, n2, n3 = X.shape
A = np.random.rand(n1, R)
B = np.random.rand(n2, R)
C = np.random.rand(n3, R)
# X按照不同模式展开
X_1 = tensor_mode_unfold(X,1)
X_2 = tensor_mode_unfold(X,2)
X_3 = tensor_mode_unfold(X,3)
# 迭代更新A、B、C
for i in range(max_iter):
# 更新A矩阵
BtB = np.dot(B.T, B)
CtC = np.dot(C.T, C)
# A = X_1 @ khatri_rao(C,B) @ (np.linalg.pinv(CtC*BtB)) #另一种更新公式
A = X_1 @ (np.linalg.pinv(khatri_rao(C,B).T))
A = np.round(A,2) #保留两位小数
# 更新B矩阵
AtA = np.dot(A.T, A)
CtC = np.dot(C.T, C)
# B = X_2 @ khatri_rao(C,A) @ (np.linalg.pinv(CtC*AtA))
B = X_2 @ (np.linalg.pinv(khatri_rao(C,A).T))
B = np.round(B,2)
# 更新C矩阵
AtA = np.dot(A.T, A)
BtB = np.dot(B.T, B)
# C = X_3 @ khatri_rao(B,A) @ (np.linalg.pinv(BtB*AtA))
C = X_3 @ (np.linalg.pinv(khatri_rao(B,A).T))
C = np.round(C,2)
# 计算目标函数值
X_pred = np.einsum('ir,jr,kr->ijk', A, B, C)
err = norm(X - X_pred) / norm(X)
# err = norm(X - X_pred)
if err < tol:
print(err)
print(X_pred)
print(i)
break
return A, B, C
X =np.array([[[21, 26, 31, 36], [43, 54, 65, 76], [65, 82, 99, 116]], [[43, 54, 65, 76], [89, 114, 139, 164], [135, 174, 213, 252]]])
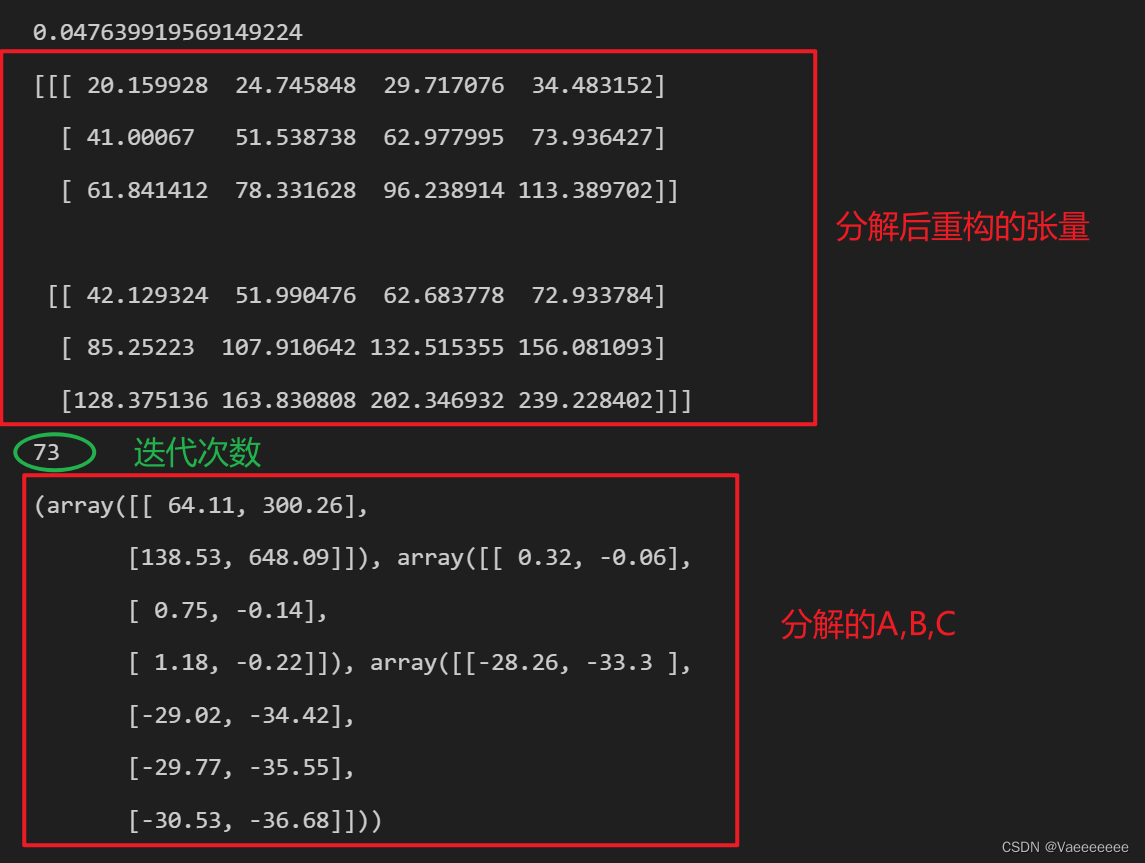
print(als_cp(X, 2, max_iter=2000, tol=0.05))
这里收敛精度取的很低,运行过程中发现如果收敛精度设置的较高,最终分解得到的全是零矩阵。
运行结果如下:
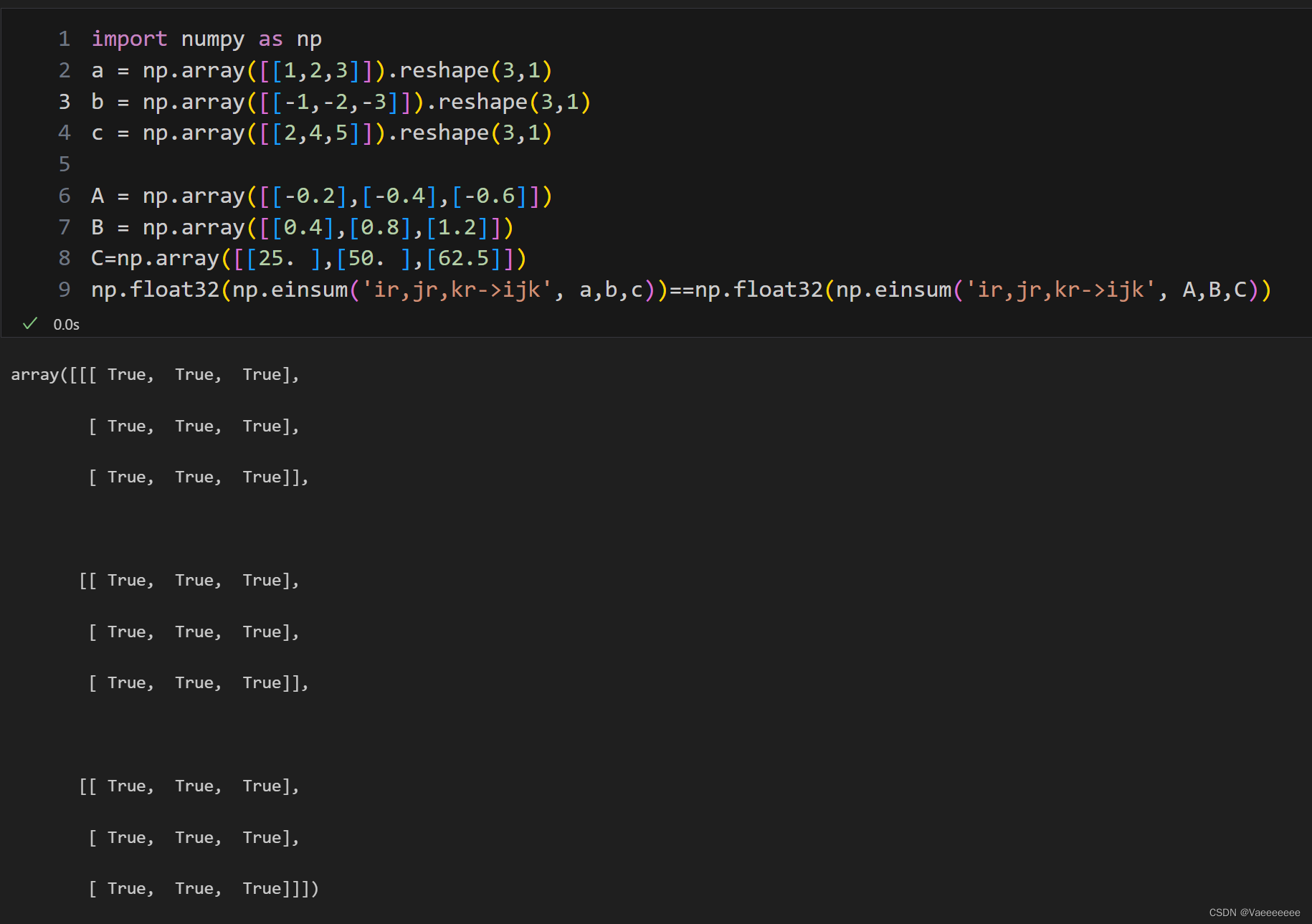
- 需要注意的是某些张量的分解结果不一定是唯一的,例子如下:
1.3.1.2 CP分解函数——parafac
- 直接看代码:
import numpy as np
import tensorly as tl
from tensorly.decomposition import parafac #CP分解
X = np.array(
[[[ -2, -4, -5],
[ -4, -8, -10],
[ -6, -12, -15]],
[[ -4, -8, -10],
[ -8, -16, -20],
[-12, -24, -30]],
[[ -6, -12, -15],
[-12, -24, -30],
[-18, -36, -45]]])
factors = parafac(X, rank=1)
print(factors.factors) #打印出分解的矩阵
print('还原结果:',tl.kruskal_to_tensor(factors))
# 或者使用 np.einsum('ir,jr,kr->ijk', factors.factors[0], factors.factors[1], factors.factors[2])
>>>[array([[-25.0998008 ],
[-50.19960159],
[-75.29940239]]), array([[0.26726124],
[0.53452248],
[0.80178373]]), array([[0.2981424 ],
[0.59628479],
[0.74535599]])]
还原结果: [[[ -2. -4. -5.]
[ -4. -8. -10.]
[ -6. -12. -15.]]
[[ -4. -8. -10.]
[ -8. -16. -20.]
[-12. -24. -30.]]
[[ -6. -12. -15.]
[-12. -24. -30.]
[-18. -36. -45.]]]
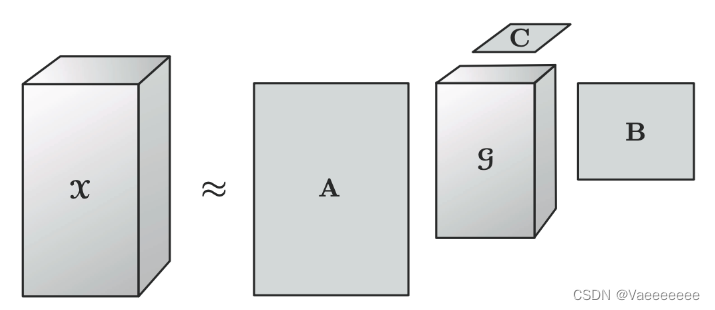
1.3.2 Tucker分解
- 一句话解释:Tucker分解算法将张量分解为核心张量在每个mode上与矩阵的乘积。
- 以一个三维张量 X ∈ R I × J × K \mathcal{X} \in \mathbb{R}^{I \times J \times K} X∈RI×J×K分解为一个核心张量 G ∈ R P × Q × R G \in \mathbb{R}^{P \times Q \times R} G∈RP×Q×R和一组矩阵 A ∈ R I × P A \in \mathbb{R}^{I \times P} A∈RI×P, B ∈ R J × Q B \in \mathbb{R}^{J \times Q} B∈RJ×Q, C ∈ R K × R C \in \mathbb{R}^{K \times R} C∈RK×R的乘积:
X
≈
G
×
1
A
×
2
B
×
3
C
\mathcal{X} \approx \mathcal{G} \times_1 A\ \times_2 B \times_3 C
X≈G×1A ×2B×3C
对于每个元素:
X
≈
∑
p
=
1
P
∑
q
=
1
Q
∑
r
=
1
R
g
p
q
r
a
i
p
b
j
q
c
k
r
对于每个元素:\mathcal{X}\approx\sum_{p=1}^{P}\sum_{q=1}^{Q}\sum_{r=1}^{R}g_{pqr}a_{ip}b_{jq}c_{kr}
对于每个元素:X≈p=1∑Pq=1∑Qr=1∑Rgpqraipbjqckr
用矩阵的形式表示:
用矩阵的形式表示:
用矩阵的形式表示:
X ( 1 ) ≈ A G ( 1 ) ( C ⊙ B ) T \mathcal{X} _{(1) }\approx AG_{(1)}(C\odot B) ^T X(1)≈AG(1)(C⊙B)T X ( 2 ) ≈ B G ( 2 ) ( C ⊙ A ) T \mathcal{X} _{(2) } \approx BG_{(2)}(C\odot A) ^T X(2)≈BG(2)(C⊙A)T X ( 3 ) ≈ C G ( 3 ) ( B ⊙ A ) T \mathcal{X} _{(3) } \approx CG_{(3)} (B\odot A) ^T \\ X(3)≈CG(3)(B⊙A)T
-
P , Q , R P,Q,R P,Q,R是对应的因子矩阵 A , B , C A,B,C A,B,C的成分数目(即列向量的数目)。
-
从上面可以发现 C P CP CP分解法其实是 T u c k k e r Tuckker Tuckker法的一个特例:
T u c k e r → 当 G 为超对角张量以及 P = Q = R 时 C P Tucker\xrightarrow{当G为超对角张量以及P=Q=R时}CP Tucker当G为超对角张量以及P=Q=R时CP
-
这里我们直接使用已有函数
tensorly.decomposition.tucker实现:
import tensorly as tl
import numpy as np
from tensorly.decomposition import tucker
X =np.array([[[21, 26, 31, 36], [43, 54, 65, 76], [65, 82, 99, 116]], [[43, 54, 65, 76], [89, 114, 139, 164], [135, 174, 213, 252]]])
core, factors = tucker(X, rank=[2,2,2]) #rank的值 = 核张量的大小
print(core)
print(core.shape)
for i in factors:
print(i)
print(i.shape)
>>>[[[ 5.40004250e+02 4.78055587e-04]
[ 1.10588415e-03 2.27895261e+00]]
[[ 8.60894313e-04 2.92055972e+00]
[ 1.28242147e+00 -2.05226289e-01]]]
(2, 2, 2)
[[ 0.42364875 0.90582655]
[ 0.90582655 -0.42364875]]
(2, 2)
[[ 0.24937424 0.87814909]
[ 0.52995313 0.22909171]
[ 0.81053203 -0.41996567]]
(3, 2)
[[ 0.34397247 0.76268141]
[ 0.44018534 0.32593997]
[ 0.53639821 -0.11080146]
[ 0.63261107 -0.5475429 ]]
(4, 2)
验证一下,看一下还原结果:
tl.tucker_to_tensor((core,factors))
#或者使用: X = np.einsum('ijk,ai,bj,ck->abc',core,factors[0],factors[1],factors[2])
>>>array([[[ 21., 26., 31., 36.],
[ 43., 54., 65., 76.],
[ 65., 82., 99., 116.]],
[[ 43., 54., 65., 76.],
[ 89., 114., 139., 164.],
[135., 174., 213., 252.]]])
1.3.2 t-SVD(张量奇异值分解)
-
T u c k e r Tucker Tucker 分解能够将高维张量分解为互不重叠的低维矩阵和核张量的乘积,是一种常用的张量分解方法。但是, T u c k e r Tucker Tucker 分解存在着许多问题:例如难以处理高阶张量、储存核张量需要大量空间等。 t − S V D t-SVD t−SVD(tensor singular value decomposition)分解就是用来解决这些问题的一种改进方法。
-
首先了解一下SVD(奇异值分解)的基本概念:
对于矩阵 A m × n A^{m\times n} Am×n,A的SVD为:
A = U Σ V T A=U\Sigma V^{T} A=UΣVT
其中 U m × m , V n × n U^{m\times m},V^{n\times n} Um×m,Vn×n都是正交矩阵, Σ m × n \Sigma^{m\times n}{} Σm×n 除主对角线上的元素以外全为0
-
t − S V D t-SVD t−SVD 算法也很类似,以三阶张量 X i × j × k \mathcal{X}^{i\times j\times k} Xi×j×k为例,经过 t − S V D t-SVD t−SVD分解(其中, S S S是对角张量):
X = U i × i × k ∗ S i × j × k ∗ V j × j × k T \mathcal{X} = U_{i\times i\times k}*S_{i\times j\times k}*V^{T}_{j\times j\times k} X=Ui×i×k∗Si×j×k∗Vj×j×kT
注意: A l × p × n A^{l\times p\times n} Al×p×n, B p × m × n B^{p\times m\times n} Bp×m×n,则 A ∗ B A*B A∗B得到大小为 l × m × n l\times m\times n l×m×n的张量 -
算法步骤:
1.4 什么是张量压缩感知
-
介绍完前面的基础知识,再进入正题🤦♂️,了解一下张量压缩感知的概念。张量压缩感知(Tensor Compressed Sensing)是一种利用稀疏性和低秩性信息来压缩张量的方法。与传统的向量或矩阵压缩感知不同,张量压缩感知可以对高阶张量进行压缩,例如视频、音频等多维信号。
-
张量压缩感知假设张量本身具有某种结构,例如低秩性或矩阵结构,从而可以使用较少的数据来恢复原始张量。这种方法在处理高维数据时具有很大的优势,可以显著减少存储和计算的成本。
-
张量压缩感知的核心就是张量分解,常用的分解方法在前文已经介绍了一些。通过在低维空间中进行张量分解,并利用稀疏表示和优化算法来实现压缩和恢复操作,可以高效地实现张量压缩感知。
张量压缩感知在计算机视觉、信号处理、语音识别等领域有着广泛的应用,可以大大提高数据的存储和传输效率。
总结
张量分解还有其他不同的算法,以后再把原理和代码一并附上。文章不足之处,欢迎指正,共同学习,共同进步。✔
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PYMGYPjT-1684332309179)(image/tensorcompression/1684331384665.png)]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvY2VhNWIzOWI3NzQ0MDJmNzg4ZjY4MzdkMGQ3YTE0ODQucG5n)