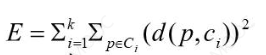1聚类

1.1聚类定义

聚类是把数据对象集合按照相似性划分为多个子集的过程。每个子集是一个簇(cluster)，使得簇中的对象彼此相似，但与其他簇中的对象不相似。
聚类是无监督学习，因为给的数据没有类标号信息。

1.2分类与聚类

分类：有监督学习；通过有标签样本学习分类器。
聚类：无监督学习；通过观察学习，将数据分隔成多个簇。

1.3聚类的应用

商业领域：聚类分析背用来发现不同的客户群，并且通过购买模式刻画不同的客户群的特征。
电子商务：聚类出具有相似浏览行为的客户，并分析客户的共同特征，可以更好的帮助电子商务的用户了解自己的客户，向客户提供更合适的服务。
舆情监控：发现热点主题、话题、事件等；发现未知异常

1.4基本聚类方法

划分方法：k-means，k-means++，k-modes，k中心点
              k-modes能够解决离散数据的聚类问题
              k-means++能够解决初始点影响聚类效果的问题
              k中心点能够解决有离群点的聚类问题
层次方法：AGNES算法，DIANA算法
基于密度的方法：DBSCAN算法，

2k-means（k-均值）算法

2.1划分方法

划分方法：将有n个对象的数据集D划分成k个簇，并且k≤n，满足如下的要求：每个簇至少包含一个对象；每个对象属于且仅属于一个簇。
基本思想：首先创建一个初始k划分（k为要构造的划分数），然后不断迭代地计算各个簇的聚类中心并根据新的聚类中心调整聚类情况，直至收敛。
目标：同一个簇中的对象之间尽可能“接近”或相关，不同簇中的对象之间尽可能“远离”或不同。
启发式方法：

            k-均值（k-means）：每个簇用该簇中对象的均值来表示；基于质心的技术
            k-中心点（k-medoids）：每个簇用接近簇中心的一个对象来表示；基于代表对象的技术
适用性：这些启发式算法适合发现中小规模数据库中的球状聚类，对于大规模数据库和任意形状的聚类，这些算法需要进一步扩展。

2.2k-means

2.2.1概念

k-means将样本集合划分为k个子集，构成k个类，将n个样本分到k个类中，使得每个样本到其所属类的中心的距离最小。

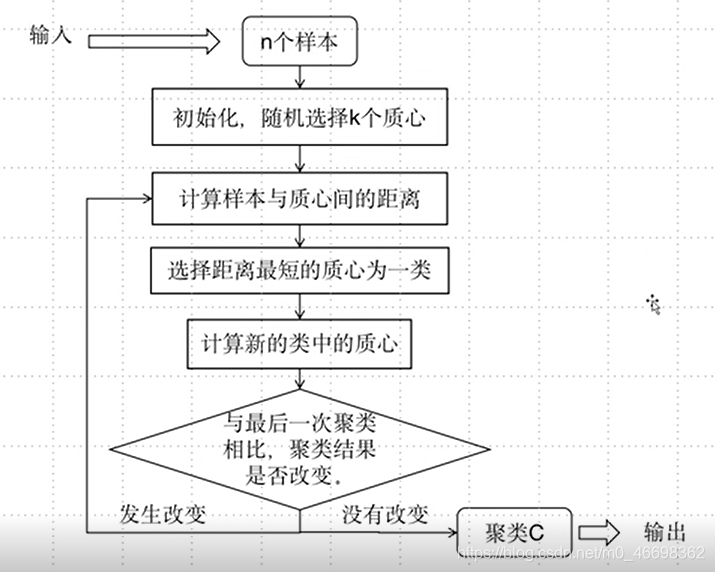
2.2.2算法描述

2.2.3步骤示例

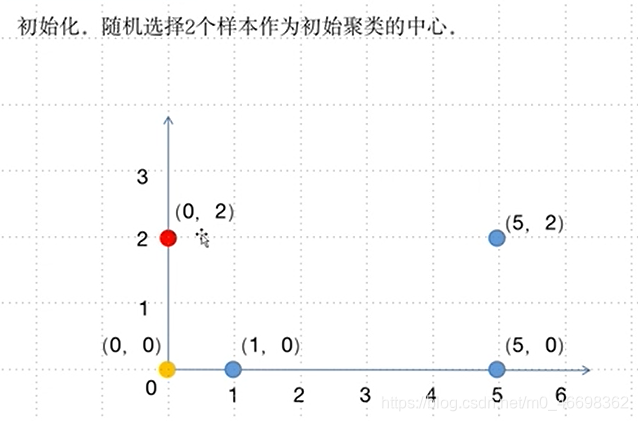
步骤一：初始化

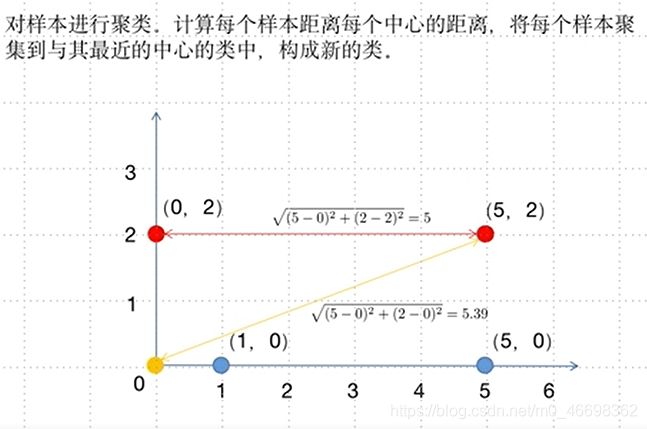
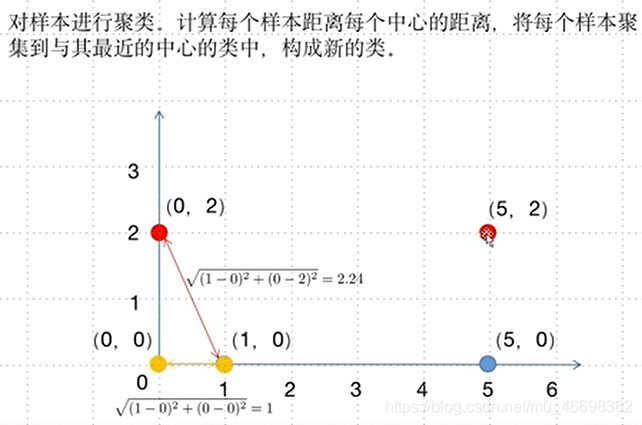
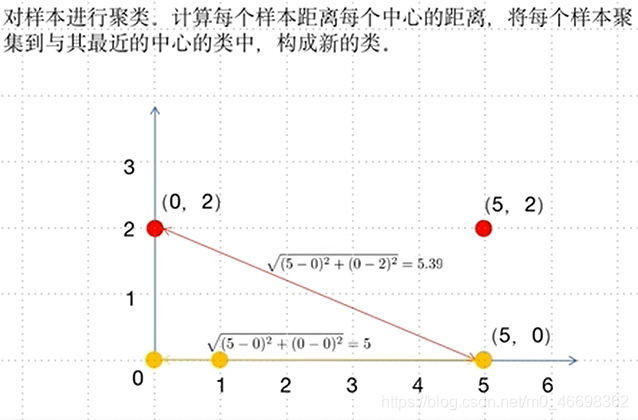
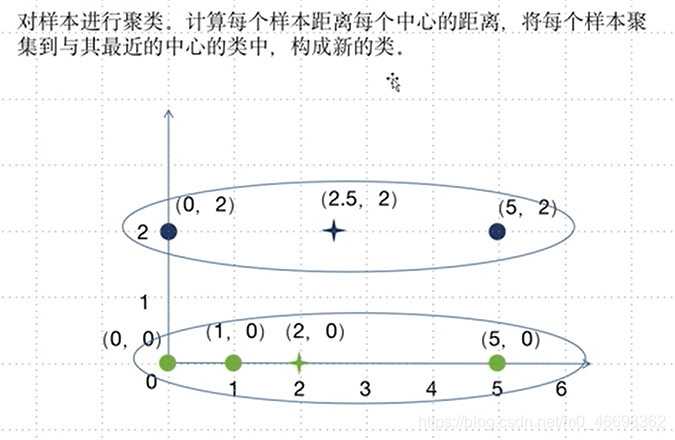
步骤二：聚类



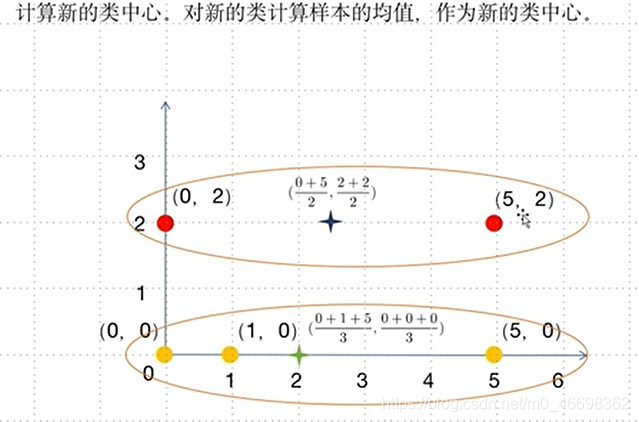
步骤三：寻找新的类中心

步骤四：重新计算距离

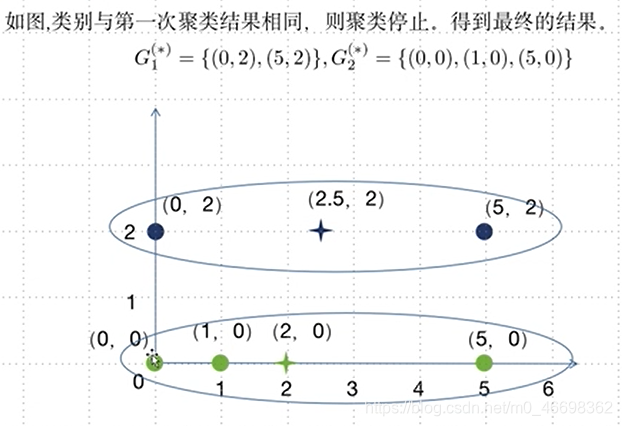
步骤五：与上一次聚类结果比较

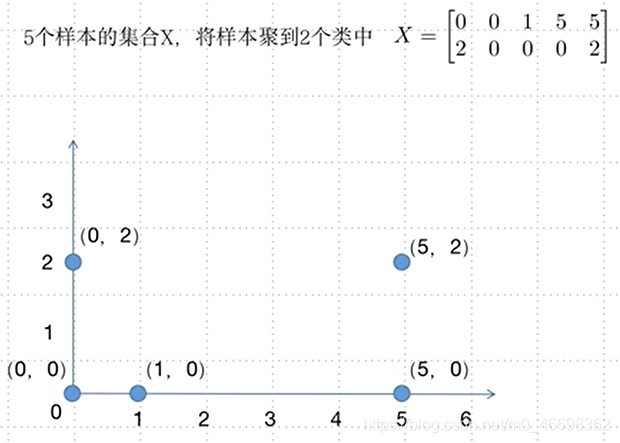
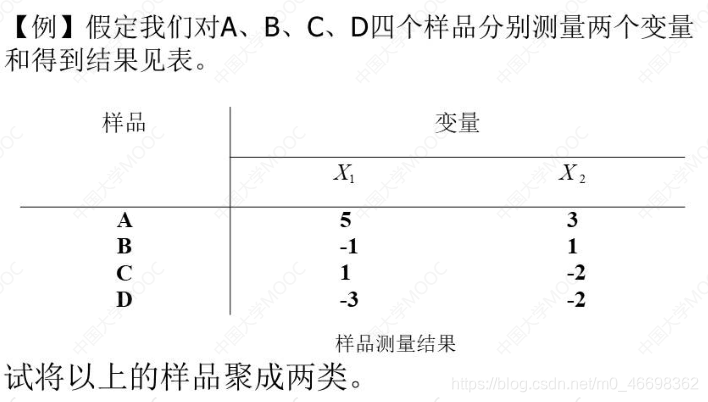
2.2.4例子

2.2.5优缺点

优点
·聚类时间快
·当结果簇是密集的,而簇与簇之间区别明显时，效果较好
·相对可扩展和有效，能对大数据集进行高效划分
缺点
.用户必须事先指定聚类簇的个数
·常常终止于局部最优
·只适用于数值属性聚类(计算均值有意义)
·对噪声和异常数据也很敏感
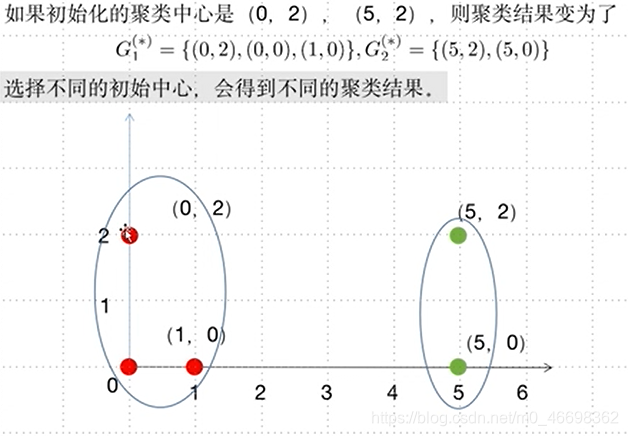
·不同的初始值,结果可能不同
.不适合发现非凸面形状的簇

k-modes算法解决数据敏感的问题

k-means++算法解决初始点选择问题

基本原理
1.从输入的数据点集合中随机选择一个点作为第一个聚类中心;
2.对于数据集中的每一个点X，计算其与聚类中心的距离D(X);
3.选择一个D(X)最大的点作为新的聚类中心;
4.重复2和3步直到K个聚类中心被选出;
5.利用K个初始聚类中心运行K-Means

k-中心点算法解决对离群点敏感问题

选用簇中位置最中心的实际对象即中心点作为参照点，基于最小化所有对象与其参照点之间的相异度之和的原则来划分(使用绝对误差标准)。
划分方法聚类质量评价准则:最小化E值