BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络模型之一
具体数学推导以及原理在本文不做详细介绍,本文将使用MATLAB进行BP神经网络的应用与实践
1 BP神经网络结构
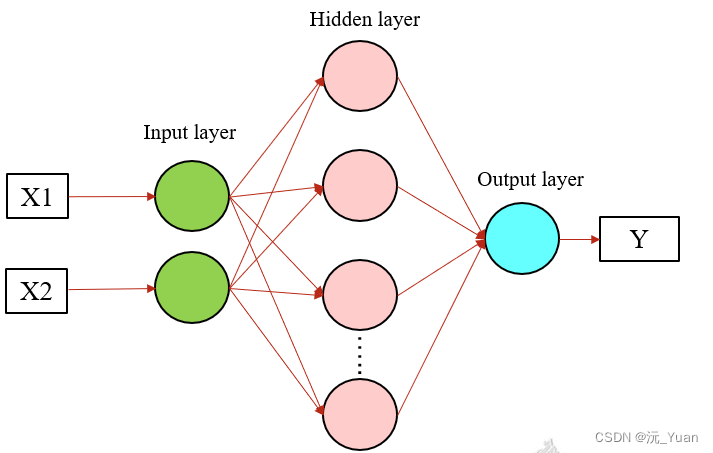
BP神经网络是一种多层前馈神经网络,其主要特点是:信号是前向传播,误差是后向传播。经典的BP神经网络具有三层网络结构,分别为输入层,隐含层,输出层。输入变量X1,X2,经过BP神经网络训练,可得到需要的预测输出Y。
2 代码结构
第一部分 初始化
使用 clear clc等命令对matlab进行初始化
第二部分 导入数据
加载数据集data.mat,此部分需要替换为自己的数据,该数据集需包含输入的X,需要预测输出的Y,然后通过dividerand函数将训练集和测试集分为7:3,也可调整为8:2。
第三部分 数据归一化
归一化是将样本的特征值转换到同一量纲下把数据映射到[-1, 1]区间内,归一化的作用以及函数的使用可以自行百度
第四部分 构造网络结构
输入层节点数是由输入数据组数决定,隐含层节点数由经验公式可得(2倍输入节点数+1),输出节点输出数据组数决定,然后使用newff进行网络训练,( { ‘logsig’ ‘purelin’ } , ‘trainlm’)此处为输入层激活函数,输出层激活函数,训练方法。
第五部分 测试集预测
使用训练好的神经网络对测试集进行测试,并显示输出相关数据。
3 Tips
1 BP神经网络每次训练结果都不一样,此为神经网络特性,选择效果好的一次网络即可,可使用save net 命令保存网络与load net加载网络命令进行复现
2 使用BP神经网络需要大量的数据训练效果才比较好
3 结果不理想时,可通过调整第四部分代码(调整训练目标,训练次数等参数)来得到较好的结果
4 有不理解的函数部分可通过查询MATLAB官方手册查询,本文不再提供代码解答
4 源代码
%% BP神经网络预测
clear
clc
close all
warning off;
tic
%% 导入数据
load data.mat
[trainInd,valInd,testInd] = dividerand(size(X,2),0.7,0,0.3);
P_train=X(:,trainInd);
T_train=Y(:,trainInd);
P_test=X(:,testInd);
T_test=Y(:,testInd);
%% 归一化
% 训练集
[Pn_train,inputps] = mapminmax(P_train,-1,1);
Pn_test = mapminmax('apply',P_test,inputps);
% 测试集
[Tn_train,outputps] = mapminmax(T_train,-1,1);
Tn_test = mapminmax('apply',T_test,outputps);
%% 构造网络结构
%创建神经网络
inputnum = 2; %inputnum 输入层节点数 4维特征
hiddennum = 5; %hiddennum 隐含层节点数
outputnum = 1; %outputnum 隐含层节点数
net = newff( minmax(Pn_train) , [hiddennum outputnum] , { 'logsig' 'purelin' } , 'trainlm' ) ;
%设置训练参数
net.trainparam.show = 50 ;
net.trainparam.epochs = 200 ;
net.trainparam.goal = 0.001 ;
net.trainParam.lr = 0.01 ;
net = train( net, Pn_train , Tn_train ) ;
%% 测试集预测
TestResults = sim(net,Pn_test);
TestResults = mapminmax('reverse',TestResults,outputps); %反归一化
TestError = TestResults - T_test;
TestMSE = mse(TestError);
figure
plot(T_test,'b-');
hold on
plot(TestResults,'r-');
legend('真实值','预测值');
title('测试集预测结果');
grid on
figure
plot(TestError,'r-');
title('测试集误差')
grid on
[~,len]=size(T_test);
MAE1=sum(abs(TestError./T_test))/len;
MSE1=TestError*TestError'/len;
RMSE1=MSE1^(1/2);
R = corrcoef(T_test,TestResults);
r = R(1,2);
disp(['........BP神经网络测试集误差计算................'])
disp(['平均绝对误差MAE为:',num2str(MAE1)])
disp(['均方误差为MSE:',num2str(MSE1)])
disp(['均方根误差RMSE为:',num2str(RMSE1)])
disp(['决定系数 R^2为:',num2str(r)])
toc