简介
朴素贝叶斯分类器(Naive Bayes Classifier 或 NBC)发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。同时,NBC模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单。理论上,NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为NBC模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,这给NBC模型的正确分类带来了一定影响。[1]
这里简单使用两张温州大学黄海广老师课件的截图来简要表示朴素贝叶斯的基本原理
X可以理解为可观测的参数,而Y则是我们所需预测的参数,利用统计学即某个确定Y的X属性占比分布来作为模型判断的基础。打个比方,我们通过一个人的体重(77kg)来预测其平均在一餐中摄入的热量,首先对建模集样本进行统计,发现75-80kg体重的人摄入热量分布600卡5%、700卡10%、800卡60%,基于这些建模集的样本统计,朴素贝叶斯给出答案:800卡(60%);在实际中案例中,这个模型还会有更多的参数,包括性别、身高、人种、生活气候等,通过各个属性概率的相乘,最后进行归一化对比,以可能性最高的情况作为预测结果。
朴素贝叶斯模型默认所有参数相互独立互补影响,但这对于日常生活中的模型是不切实际的,因此当建模对象的参数有明显的共线性问题时,使用朴素贝叶斯的方法就不太合适了。
下面提供参考的代码段:
代码脚本:
%Foddcus 2022.3
%朴素贝叶斯脚本
%输入:input 具有离散属性的数据、或已经分割好的数据 分类在第一列
%标准的贝叶斯数据处理,输出可以直接储存
clear all
input=xlsread("D:\同步空间\采集数据库\缺素\10.xlsx");
inform=[1111,1112,1113,1114];
errorF=CKOpatua(input,inform,20,0);
input=DLrow(input,errorF)
input=input(:,2:20);%删除序号
y=evaluatenNavieByes(input,inform);%测试最佳的分段数,y为分段数
[input2,D]=DSTparameter(input,y,0,0);%将离散的属性参数进行分段分类
maxnum=max(input2);
[XSelected,XRest,vSelectedRowIndex]=selectSam(input2,0.2);%提取20%的样本作为预测集,80%的样本为建模集
[modeIFMT,checkout,corr]=naviebyes(XRest,inform,maxnum);%建立朴素贝叶斯模型
[checkout2,corr2]=NbyesPre(XSelected,inform,modeIFMT,maxnum);%就模型对新的样本进行预测
Cmatrix=CFSmatrix(checkout2,inform);%就预测效果生成混淆矩阵
其中运用到的自定义函数:
1.errorF=CKOpatua(input,inform,20,0);异常数据检验函数,
matlab 基于拉依达检验法(3σ准则) 实现多类别多参数的批量检验异常值与异常样本_foddcusL的博客-CSDN博客_拉依达检验法
2.input=DLrow(input,errorF);删除目标行(即异常样本)
matlab 批量删除数组的行_foddcusL的博客-CSDN博客
3.y=evaluatenNavieByes(input,inform);
因为案例中我输入的数据是一个连续的离散数据,而朴素贝叶斯的分类是基于属性分类的统计进行建模,所以我们要先尝试不同分段数下建模效果的准确率,取准确率最高的分段数作为建模分段数。
%评价当前数据用贝叶斯评价的的适合参数 评估范围是2:50
%xf,xe为参数的范围,xf一般从2开始取 第一列为标识码
%输入:input:excel文件夹, inform=[1111,1112,1113,1114,1115];
%输出:y:最佳的分割段数
function y=evaluatenNavieByes(input,inform);
for i=2:50
for j=1:10
disp([i,j]);
[input2,D]=DSTparameter(input,i,0,0);
maxnum=max(input2);
[XSelected,XRest,vSelectedRowIndex]=selectSam(input2,0.2);
[modeIFMT,checkout,corr]=naviebyes(XRest,inform,maxnum);%建模
[checkout2,corr2]=NbyesPre(XSelected,inform,modeIFMT,maxnum);
corrF(i,j)=corr;
corrF2(i,j)=corr2;
end
disp('correct');
end
corrZ=mean(corrF,2);
corrZ2=mean(corrF2,2);
corrZ3=corrZ.*corrZ2;%预测集准确率与建模集集准确率相乘
for i=1:50
corrZ3(i,1)=corrZ3(i,1)-0.2*i;%正则率取0.2%较佳
end
[x,y]=max(corrZ3);%取最高的准确率
end4:[input2,D]=DSTparameter(input,i,0,0);将离散的参数分段
%%使用相对标准差将数据分割成数个区间,分成区间数为相对标准差*6
%第一列为识别码
%输入:excel数据:input xf,xe为参数的范围 一般第一列为识别码,xf从2开始取
%输出:分类后的数据:output D分割取值和最小值,方便后期对其他数据进行处理
function [output,D]=DSTparameter(input,muti,xfFxx,xeFxx)
[ys,xs]=size(input);
if xfFxx==0||xeFxx==0%这个判断会收到外部因素影响,所以加个后缀
xfFxx=2;
xeFxx=xs;
else
input=[input(:,1),input(:,xfFxx:xeFxx)];%设定区间
end
S_row=std(input);
M_row=mean(input);
SBS=round(muti*S_row./M_row);%向上取整
Maxrow=max(input);
Minrow=min(input);
D=(Maxrow-Minrow)./SBS;
for i=xfFxx:xeFxx
for j=1:ys
for k=1:SBS(1,i)
if (Minrow(1,i)+D(1,i)*(k-1))<=input(j,i)&&input(j,i)<=(Minrow(1,i)+D(1,i)*k)
output(j,i)=k;
end
end
end
end
output(:,1)=input(:,1);
D=[Minrow;D];
end5:[XSelected,XRest,vSelectedRowIndex]=selectSam(input2,0.2);随机提取样本
随机提取excel中的行 自定义函数_foddcusL的博客-CSDN博客
6: [modeIFMT,checkout,corr]=naviebyes(XRest,inform,maxnum);根据数据集进行朴素贝叶斯建模
%author LijiaYi FAFU 2022.3
%朴素贝叶斯建模
% 输入:input 具有离散属性的数据、或已经分段判别好的数据 属性判别在第一列,且所有数据都在第一行
% inform数据标识(一行多列的矩阵) max:每个属性最大值的单行多列矩阵
% 输出: modeIFMT模型内容,新内容加到3维阵的最后一列 checkout 输出本身的检查结果
% corr自检准确率
function [modeIFMT,checkout,corr]=naviebyes(input,inform,maxnum)
modeIFMT=[];
[yn,xn]=size(inform);
[ys,xs]=size(input);
for i=2:xs
for j=1:maxnum(1,i)%j为属性值
[indexF,input2]=DSTname(input,[j],i); %输出1维的矩阵 ,若未有其值,则输出空矩阵
for ctg=1:xn
if isempty(input2)%判断是否为空矩阵
modeIFMT(j,i-1,ctg)=0;
else
name=inform(1,ctg);
index=find(input2(:,1)==name);%判断这个属性各个于类别中的占比,转化为0-1之间的数
[ys2,xs2]=size(index);
modeIFMT(j,i-1,ctg)=ys2/ys;
end
end
end
%输出属性在某个类别的占比
end
%自检
dnum=modeIFMT(1,1,:);
for i=1:ys
for j=2:xs
for attri=1:maxnum(1,j)
if find(input(i,j)==attri)
for ctg=1:xn
build(ctg,j-1)=modeIFMT(attri,j-1,ctg);
end
end
end
end
prob=ones(xn,1);
for j=1:xs-1
prob=prob.*build(:,j);
end
[pbb,ys3]=max(prob);
checkout(i,2)=max(prob)/sum(prob);
checkout(i,1)=inform(1,ys3);
end
n=0;
for i=1:ys
if checkout(i,1)==input(i,1)
n=n+1;
end
end
corr=n/ys;
checkout=[input(:,1),checkout];
end7:[checkout2,corr2]=NbyesPre(XSelected,inform,modeIFMT,maxnum);根据模型对预测集进行预测
%朴素贝叶斯预测
%输入:input 具有离散属性的数据、或已经分段判别好的数据 属性判别在第一列,且所有数据都在第一行
%inform数据标识(一行多列的矩阵) max:每个属性最大值的单行多列矩阵
%输出: modeIFMT模型内容,新内容加到3维阵的最后一列 checkout 输出本身的检查结果
%corr自检准确率
% clear all
% load("D:\同步空间\算法汇总\机器学习\data\naviebyes1.mat")
function [checkout,corr]=NbyesPre(input,inform,modeIFMT,maxnum)
[yn,xn]=size(inform);
[ys,xs]=size(input);
dnum=modeIFMT(1,1,:);
nk=0;
for i=1:ys
for j=2:xs
for attri=1:maxnum(1,j)
if find(input(i,j)==attri)%确定属性值,若为已存在在属性值
for ctg=1:xn
build(ctg,j-1)=modeIFMT(attri,j-1,ctg);%buid为该样本在该条件下,各个种类可能值
end
nk=1;
end
end
if nk==0%如果没有找到该位置的属性,为其赋值0
build(ctg,j-1)=0
end
nk=0;
end
prob=ones(xn,1);
errorP=max(build);
for j=1:xs-1
if find(errorP(1,j)==0)
prob=prob.*ones(xn,1);
else
prob=prob.*build(:,j);
end
end
[pbb,ys3]=max(prob);
checkout(i,2)=max(prob)/sum(prob);
checkout(i,1)=inform(1,ys3);
end
n=0;
for i=1:ys
if checkout(i,1)==input(i,1)
n=n+1;
end
end
corr=n/ys;
checkout=[input(:,1),checkout];
end8:Cmatrix=CFSmatrix(checkout2,inform);%就预测效果生成混淆矩阵
matlab 混淆矩阵 自定义函数_foddcusL的博客-CSDN博客
9:[indexF,output]=DSTname(datadet,CTGname,where);根据样本名称分类的自定义函数
%输入
%datadet原始数据
%CTGname:分类名称(一行二维矩阵格式),类别名称应为第where列
%输出
%indexF:各类所在的行
%output:分好类的三维矩阵(按最大二维矩阵输出二维尺寸,其他会有含零的层
function [indexF,output]=DSTname(datadet,CTGname,where)
output=[];
[ys,xs]=size(CTGname);
for i=1:xs
indexForlist=find(datadet(:,where)==CTGname(1,i));
[indexR,indexL]=size(indexForlist);
indexF(1:indexR,i)=indexForlist(:,1);
for j=1:indexR%将选中的数据分开存放
output(j,:,i)=[datadet(indexForlist(j,1),:)];%数据开头是该行数据在原本excel中的行数
end
end
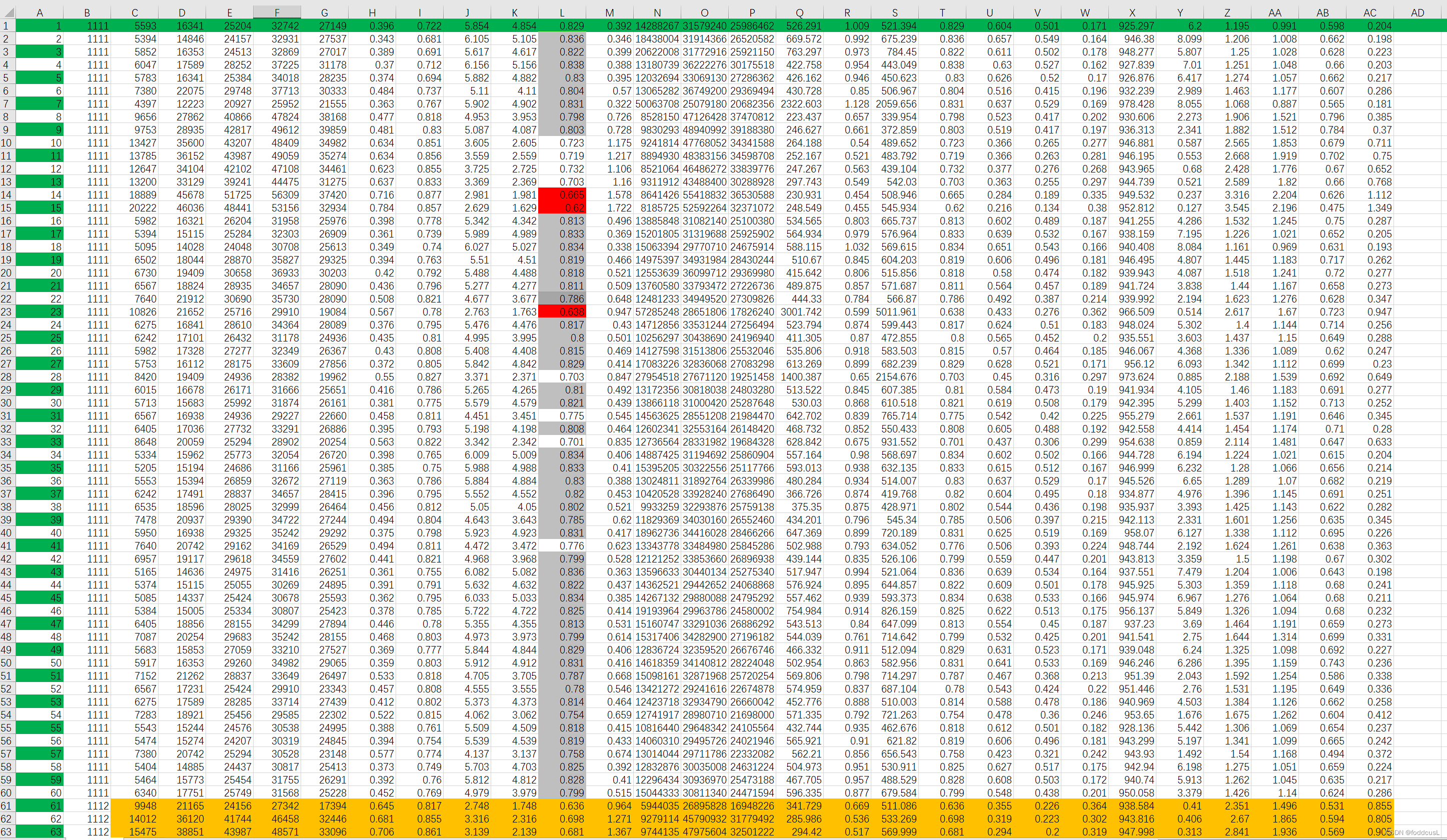
案例展示:
输入表格:input:
第一列为样本的序号,第二列为样本的分类数值代号分别为1111,1112,1113、1114,对应inform的数据,后续皆为样本的参数。
输出:
corr、corr2;分别是建模集和预测集的准确率;朴素贝叶斯非常依赖建模样本的稳定程度,只有当样本参数够多,样本量较大,数据准确,才会有极高的预测准确度。
modelFMT:生成的模型;
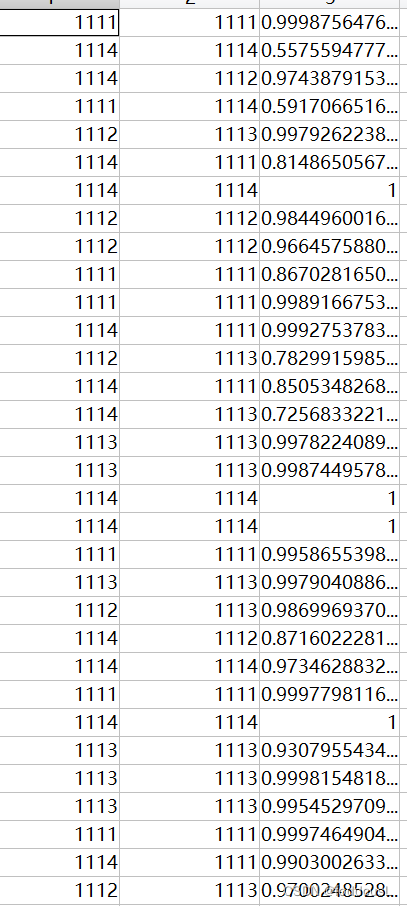
checkout、checkout2:预测表,第一列为真实值;第二列为预测值,第三列为把握;
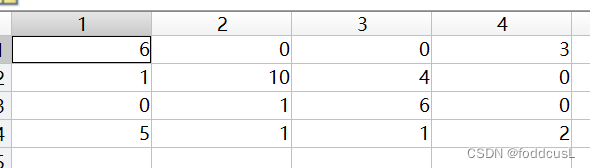
Cmatrix:生成的混合矩阵,4*4,表头对应inform的内容