目录
和组合导航一样,也可以通过预积分 IMU 因子加上雷达残差来实现基于预积分和图优化的紧耦合 LIO 系统。一些现代的 Lidar SLAM 系统也采用了这种方式。相比滤波器方法来说,预积分因子可以更方便地整合到现有的优化框架中,从开发到实现都更为便捷。
1 预积分 LIO 系统的经验
在实现当中,预积分的使用方式是相当灵活的,要设置的参数也比 EKF 系统更多。例如 LIO-SAM 把预积分因子与雷达里程计的因子相结合,来构建整个优化问题。而在 VSLAM 系统里,也可以把预积分因子与重投影误差结合起来去求解 Bundle Adjustment。我们在此介绍一些预积分应用上的经验:
- 1. 预积分因子通常关联两个关键帧的高维状态(典型的 15 维状态
)。在转换为图优化问题时,我们可以选择①把各顶点分开处理,例如 SE(3) 一个顶点,v 占一个顶点,然后让一个预积分边关联到 8 个顶点上;②也可以选择把高维状态写成一个顶点,而预积分边关联两个顶点,但雅可比矩阵含有大量的零块。在本节实际操作中,我们选择前一种做法,即顶点种类数量较多,但边的维度较低的写法。这里使用和 《自动驾驶与机器人中的SLAM技术》ch4:预积分学 中一样的散装的形式。
- 2. 由于预积分因子关联的变量较多,且观测量大部分是状态变量的差值,我们应该对状态变量有足够的观测和约束,否则整个状态变量容易在零空间内自由变动。例如预积分的速度观测
描述了两个关键帧速度之差。如果我们将两个关键帧的速度都增量固定值,也可以让速度项误差保持不变,而在位移项施加一些调整,还能让位移部分观测保持不变。因此,在实际使用中,我们会给前一个关键帧施加先验约束,给后一个关键帧施加观测约束,让整个优化问题限制在一定的范围内。
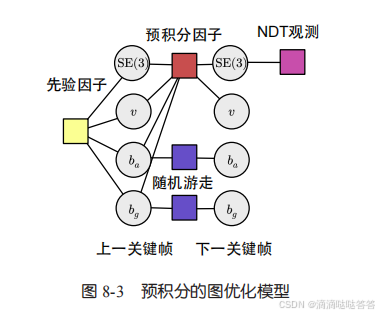
- 3. 预积分的图优化模型如下图。我们在对两个关键帧计算优化时,为上一个关键帧添加一个先验因子,然后在两个帧间添加预积分因子和零偏随机游走因子,最后在下一个关键帧中添加 NDT 观测的位姿约束。在本轮优化完成后,我们利用边缘化方法,求出下一关键帧位姿的协方差矩阵,作为下一轮优化的先验因子来使用。
- 4. 这个图优化模型和第 4 章中的 GINS 系统非常相似。但是我们应当注意到,雷达里程计的观测位姿是依赖预测数据(初始值)的,这和 RTK 的位姿观测(绝对位姿观测)有着本质区别。如果 RTK 信号良好,我们可以认为 RTK 的观测有着固定的精度,此时滤波器和图优化器都可以保证在位移和旋转方面收敛。然而,如果雷达里程计使用一个不准确的预测位姿,它很有可能给出一个不正常的观测位姿,进而使整个 LIO 发散。这也导致了基于图优化的 LIO 系统调试难度要明显大于 GINS 系统。
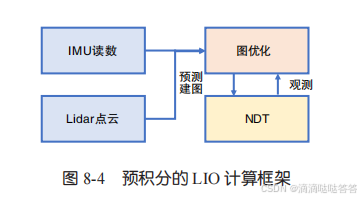
- 5. 为了重复使用 《自动驾驶与机器人中的SLAM技术》ch8:基于 IESKF 的紧耦合 LIO 系统 中的代码,我们仍然使用前文所用的 LIO 框架,只是将原先 IESKF 处理的预测和观测部分,变为预积分器的预测和观测部分(在实际的系统中,也可以将滤波器作为前端,把图优化当成关键帧后端来使用)。整个 LIO 的计算框架图如下图所示。我们会在两个点云之间使用预积分进行优化。当然,正如我们前面所说,预积分的使用方式十分灵活,读者不必拘泥于我们的实现方式,也可以使用更长时间的预积分优化,或者将 NDT 内部的残差放到图优化中。但相对的,由于预积分因子关联的顶点较多,实际调试会比较困难,容易造成误差发散的情况。从一个现有系统出发再进行后端优化是个不错的选择。
2 预积分图优化的顶点
这里图优化的顶点 和 《自动驾驶与机器人中的SLAM技术》ch4:基于预积分和图优化的 GINS 中一样,为 15 维的位姿(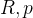
3 预积分图优化的边
这里的图优化边包括:
- 预积分边(观测值维度为 9 维的多元边):ch4:预积分学 中介绍。
- 零偏随机游走边(观测值维度为 3 维的双元边):ch4:基于预积分和图优化的 GINS 中介绍。
- 先验因子边(观测值维度为 15 维的多元边):ch4:基于预积分和图优化的 GINS 中介绍。
- NDT 观测边(观测值维度为 6 维的单元边):和双天线的 GNSS 观测边一致,在 ch4:基于预积分和图优化的 GINS 中介绍。
3.1 NDT 残差边(观测值维度为 3 维的单元边)
注意(前面提到的): 广义地说,只要我们设计的状态估计系统考虑了各传感器内在的性质,而非模块化地将它们的输出进行融合,就可以称为紧耦合系统。例如,考虑了 IMU 观测噪声和零偏的系统,就可以称为 IMU的(或 INS 的)紧耦合;考虑了激光的配准残差,就可以称为激光的紧耦合;考虑了视觉特征点的重投影误差,或者考虑了 RTK 的细分状态、搜星数等信息,就可以称为视觉或 RTK 的紧耦合。
在 ch8:基于 IESKF 的紧耦合 LIO 系统 中,我们即考虑了 IMU 的观测噪声和零偏,又考虑了激光的配准残差(NDT 残差),所以可以称之为紧耦合的 LIO 系统;但是在这里,我们只考虑的 IMU 的观测噪声和零偏,并没有考虑点云的配准残差,严格来说不能称之为紧耦合的 LIO 系统。但是在 slam_in_autonomous_driving/src/common/g2o_types.h 和 slam_in_autonomous_driving/src/ch7/ndt_inc.cc中,实现了 NDT残差边(EdgeNDT类)和 根据估计的NDT建立edges的函数(IncNdt3d::BuildNDTEdges()),本章中并没有使用这里介绍的NDT残差边,后续可将其加入到图优化中。
残差的定义:
假设图 8.3 中的上一个关键帧是 
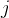
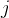
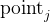
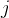
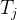
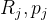
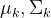
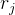
残差对状态变量的雅可比矩阵:
slam_in_autonomous_driving/src/common/g2o_types.h
/**
* NDT误差模型
* 残差是 Rp+t-mu,info为NDT内部估计的info
* 观测值维度为 3 维的单元边
*/
class EdgeNDT : public g2o::BaseUnaryEdge<3, Vec3d, VertexPose> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
EdgeNDT() = default;
/// 需要查询NDT内部的体素,这里用一个函数式给设置过去
// 该函数已实现,在 IncNdt3d::BuildNDTEdges() 函数内部
using QueryVoxelFunc = std::function<bool(const Vec3d& query_pt, Vec3d& mu, Mat3d& info)>;
EdgeNDT(VertexPose* v0, const Vec3d& pt, QueryVoxelFunc func) {
setVertex(0, v0);
pt_ = pt;
query_ = func;
Vec3d q = v0->estimate().so3() * pt_ + v0->estimate().translation();
if (query_(q, mu_, info_)) {
setInformation(info_);
valid_ = true;
} else {
valid_ = false;
}
}
bool IsValid() const { return valid_; }
Mat6d GetHessian() {
linearizeOplus();
return _jacobianOplusXi.transpose() * info_ * _jacobianOplusXi;
}
/// 残差计算
void computeError() override {
VertexPose* v0 = (VertexPose*)_vertices[0];
Vec3d q = v0->estimate().so3() * pt_ + v0->estimate().translation();
if (query_(q, mu_, info_)) {
_error = q - mu_;
setInformation(info_);
valid_ = true;
} else {
valid_ = false;
_error.setZero();
setLevel(1);
}
}
/// 线性化
void linearizeOplus() override {
if (valid_) {
VertexPose* v0 = (VertexPose*)_vertices[0];
SO3 R = v0->estimate().so3();
_jacobianOplusXi.setZero();
_jacobianOplusXi.block<3, 3>(0, 0) = -R.matrix() * SO3::hat(pt_); // 对R
_jacobianOplusXi.block<3, 3>(0, 3) = Mat3d::Identity(); // 对p
} else {
_jacobianOplusXi.setZero();
}
}
virtual bool read(std::istream& in) { return true; }
virtual bool write(std::ostream& out) const { return true; }
private:
QueryVoxelFunc query_;
Vec3d pt_ = Vec3d::Zero();
Vec3d mu_ = Vec3d::Zero();
Mat3d info_ = Mat3d::Identity();
bool valid_ = false;
};根据估计的NDT(local map)建立 NDT残差边 :
slam_in_autonomous_driving/src/ch7/ndt_inc.cc
/**
* 根据估计的NDT建立edges
* @param v :输入参数,位姿顶点
* @param edges :输出参数,全部的有效的NDT残差边
*/
void IncNdt3d::BuildNDTEdges(sad::VertexPose* v, std::vector<EdgeNDT*>& edges) {
assert(grids_.empty() == false);
SE3 pose = v->estimate();
/// 整体流程和NDT一致,只是把查询函数放到edge内部,建立和v绑定的边
for (const auto& pt : source_->points) {
Vec3d q = ToVec3d(pt);
auto edge = new EdgeNDT(v, q, [this](const Vec3d& qs, Vec3d& mu, Mat3d& info) -> bool {
Vec3i key = CastToInt(Vec3d(qs * options_.inv_voxel_size_));
auto it = grids_.find(key);
/// 这里要检查高斯分布是否已经估计
if (it != grids_.end() && it->second->second.ndt_estimated_) {
auto& v = it->second->second; // voxel
mu = v.mu_;
info = v.info_;
return true;
} else {
return false;
}
});
if (edge->IsValid()) {
edges.emplace_back(edge);
} else {
delete edge;
}
}
}
4 基于预积分和图优化 LIO 系统的实现
基于预积分的紧耦合 LioPreinteg类 持有一个 IncNdt3d 对象,一个 IMUPreintegration 对象,一个 MessageSync 对象 处理同步之后的点云和 IMU。该类处理流程非常简单:当 MeasureGroup 到达后,在 IMU 未初始化时,使用第 3 章的静止初始化来估计 IMU 零偏。初始化完毕后,预积分 IMU 数据进行预测,再用预测数据对点云去畸变,最后对去畸变的点云做配准。
void LioPreinteg::ProcessMeasurements(const MeasureGroup &meas) {
LOG(INFO) << "call meas, imu: " << meas.imu_.size() << ", lidar pts: " << meas.lidar_->size();
measures_ = meas;
if (imu_need_init_) {
// 初始化IMU系统
TryInitIMU();
return;
}
// 利用IMU数据进行状态预测
Predict();
// 对点云去畸变
Undistort();
// 配准
Align();
}4.1 IMU 静止初始化
IMU 的静止初始化与《自动驾驶与机器人中的SLAM技术》ch3:惯性导航与组合导航 中介绍的大体一致。当 MeasureGroup 到达后,在 IMU 未初始化时,调用 StaticIMUInit::AddIMU() 函数进行 IMU的静止初始化。
当 IMU 初始化成功时,在当前 MeasureGroup 中使用 IMU 静止初始化结果初始化了 陀螺仪和加速度计的噪声标准差、初始的 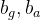
void LioPreinteg::TryInitIMU() {
for (auto imu : measures_.imu_) {
imu_init_.AddIMU(*imu);
}
if (imu_init_.InitSuccess()) {
// 读取初始零偏,设置ESKF
// 噪声由初始化器估计
options_.preinteg_options_.noise_gyro_ = sqrt(imu_init_.GetCovGyro()[0]);
options_.preinteg_options_.noise_acce_ = sqrt(imu_init_.GetCovAcce()[0]);
options_.preinteg_options_.init_ba_ = imu_init_.GetInitBa();
options_.preinteg_options_.init_bg_ = imu_init_.GetInitBg();
preinteg_ = std::make_shared<IMUPreintegration>(options_.preinteg_options_);
imu_need_init_ = false;
current_nav_state_.v_.setZero();
current_nav_state_.bg_ = imu_init_.GetInitBg();
current_nav_state_.ba_ = imu_init_.GetInitBa();
current_nav_state_.timestamp_ = measures_.imu_.back()->timestamp_;
last_nav_state_ = current_nav_state_;
last_imu_ = measures_.imu_.back();
LOG(INFO) << "IMU初始化成功";
}
}4.2 使用预积分预测
和基于 IESKF 的紧耦合 LIO 系统不同,这里使用了 IMU 预积分进行预测:
void LioPreinteg::Predict() {
// 这里会清空 imu_states_ ,所以在每接收一个 MeasureGroup 时,imu_states_ 中会存储 measures_.imu_.size() + 1 个数据,用于去畸变
imu_states_.clear();
imu_states_.emplace_back(last_nav_state_);
/// 对IMU状态进行预测
for (auto &imu : measures_.imu_) {
if (last_imu_ != nullptr) {
preinteg_->Integrate(*imu, imu->timestamp_ - last_imu_->timestamp_);
}
last_imu_ = imu;
imu_states_.emplace_back(preinteg_->Predict(last_nav_state_, imu_init_.GetGravity()));
}
}4.3 使用 IMU 预测位姿进行运动补偿
和 《自动驾驶与机器人中的SLAM技术》ch8:基于 IESKF 的紧耦合 LIO 系统 中介绍的一样,不再介绍。
4.4 位姿配准部分
在配准时,使用预积分给出的预测位姿作为增量NDT里程计的初始位姿输入,迭代得到优化后的位姿,将优化后的位姿作为观测值进行优化(即作为 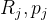
void LioPreinteg::Align() {
FullCloudPtr scan_undistort_trans(new FullPointCloudType);
pcl::transformPointCloud(*scan_undistort_, *scan_undistort_trans, TIL_.matrix().cast<float>());
scan_undistort_ = scan_undistort_trans;
current_scan_ = ConvertToCloud<FullPointType>(scan_undistort_);
// voxel 之
pcl::VoxelGrid<PointType> voxel;
voxel.setLeafSize(0.5, 0.5, 0.5);
voxel.setInputCloud(current_scan_);
CloudPtr current_scan_filter(new PointCloudType);
voxel.filter(*current_scan_filter);
/// the first scan
if (flg_first_scan_) {
ndt_.AddCloud(current_scan_);
// my 我认为这里应该添加如下代码
// current_nav_state_ = imu_states_.back();
// NormalizeVelocity();
// last_nav_state_ = current_nav_state_;
// 重置预积分 preinteg_
preinteg_ = std::make_shared<IMUPreintegration>(options_.preinteg_options_);
flg_first_scan_ = false;
return;
}
// 后续的scan,使用NDT配合pose进行更新
LOG(INFO) << "=== frame " << frame_num_;
ndt_.SetSource(current_scan_filter);
current_nav_state_ = preinteg_->Predict(last_nav_state_, imu_init_.GetGravity());
ndt_pose_ = current_nav_state_.GetSE3();
// 使用 IMU 预积分预测值作为配准初始值
ndt_.AlignNdt(ndt_pose_);
Optimize();
// 若运动了一定范围,则把点云放入地图中
SE3 current_pose = current_nav_state_.GetSE3();
SE3 delta_pose = last_ndt_pose_.inverse() * current_pose;
if (delta_pose.translation().norm() > 0.3 || delta_pose.so3().log().norm() > math::deg2rad(5.0)) {
// 将地图合入NDT中
CloudPtr current_scan_world(new PointCloudType);
pcl::transformPointCloud(*current_scan_filter, *current_scan_world, current_pose.matrix());
ndt_.AddCloud(current_scan_world);
last_ndt_pose_ = current_pose;
}
// 放入UI
if (ui_) {
ui_->UpdateScan(current_scan_, current_nav_state_.GetSE3()); // 转成Lidar Pose传给UI
ui_->UpdateNavState(current_nav_state_);
}
frame_num_++;
}4.5 图优化部分
图优化部分基本上和 ch4:基于预积分和图优化的 GINS 一样,不同之处在于一下几点:
- 1.使用了NDT优化后的位姿作为
时刻位姿顶点的初始估计值,而没有使用预积分预测的位姿;
// 本时刻顶点,pose, v, bg, ba
auto v1_pose = new VertexPose();
v1_pose->setId(4);
// 注意:这里使用NDT优化后的位姿作为 j 时刻位姿的初始估计值
v1_pose->setEstimate(ndt_pose_); // NDT pose作为初值
// v1_pose->setEstimate(current_nav_state_.GetSE3()); // 预测的pose作为初值
optimizer.addVertex(v1_pose);- 2.在优化过程中,使用 setFixed() 函数将
时刻的
和
节点视为固定节点,不进行优化;
// 在优化过程中,将 i 时刻的bg和ba节点视为固定节点,不进行优化
v0_bg->setFixed(true);
v0_ba->setFixed(true);- 3.对于
,我们想将
中的
边缘化(对应 Hessian 矩阵中 15x15 的
,要求其逆,从而消去
,边缘化
),得到
时刻状态的信息矩阵(更新后的 15x15维 的
),作为下一轮优化时(
时刻和
时刻)
时刻的先验因子的信息矩阵。在本博客的 4.6 小节中详细介绍;
- 4.对速度进行了限制,将其限制在正常区间。
void LioPreinteg::NormalizeVelocity() {
/// 限制v的变化
/// 一般是-y 方向速度
// 将车体坐标系下 y 方向的分速度限制在 (-2 到 0 之间)
Vec3d v_body = current_nav_state_.R_.inverse() * current_nav_state_.v_;
if (v_body[1] > 0) {
v_body[1] = 0;
}
// 将车体坐标系下 z 方向的分速度限制为 0
v_body[2] = 0;
if (v_body[1] < -2.0) {
v_body[1] = -2.0;
}
// 将车体坐标系下 x 方向的分速度限制在(-0.1 到 0.1 之间)
if (v_body[0] > 0.1) {
v_body[0] = 0.1;
} else if (v_body[0] < -0.1) {
v_body[0] = -0.1;
}
current_nav_state_.v_ = current_nav_state_.R_ * v_body;
}优化部分代码如下所示:
void LioPreinteg::Optimize() {
// 调用g2o求解优化问题
// 上一个state到本时刻state的预积分因子,本时刻的NDT因子
LOG(INFO) << " === optimizing frame " << frame_num_ << " === "
<< ", dt: " << preinteg_->dt_;
/// NOTE 这些东西是对参数非常敏感的。相差几个数量级的话,容易出现优化不动的情况
using BlockSolverType = g2o::BlockSolverX;
using LinearSolverType = g2o::LinearSolverEigen<BlockSolverType::PoseMatrixType>;
auto *solver = new g2o::OptimizationAlgorithmLevenberg(
g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm(solver);
// 上时刻顶点, pose, v, bg, ba
auto v0_pose = new VertexPose();
v0_pose->setId(0);
v0_pose->setEstimate(last_nav_state_.GetSE3());
optimizer.addVertex(v0_pose);
auto v0_vel = new VertexVelocity();
v0_vel->setId(1);
v0_vel->setEstimate(last_nav_state_.v_);
optimizer.addVertex(v0_vel);
auto v0_bg = new VertexGyroBias();
v0_bg->setId(2);
v0_bg->setEstimate(last_nav_state_.bg_);
optimizer.addVertex(v0_bg);
auto v0_ba = new VertexAccBias();
v0_ba->setId(3);
v0_ba->setEstimate(last_nav_state_.ba_);
optimizer.addVertex(v0_ba);
// 本时刻顶点,pose, v, bg, ba
auto v1_pose = new VertexPose();
v1_pose->setId(4);
// 注意:这里使用NDT优化后的位姿作为 j 时刻位姿的初始估计值
v1_pose->setEstimate(ndt_pose_); // NDT pose作为初值
// v1_pose->setEstimate(current_nav_state_.GetSE3()); // 预测的pose作为初值
optimizer.addVertex(v1_pose);
auto v1_vel = new VertexVelocity();
v1_vel->setId(5);
v1_vel->setEstimate(current_nav_state_.v_);
optimizer.addVertex(v1_vel);
auto v1_bg = new VertexGyroBias();
v1_bg->setId(6);
v1_bg->setEstimate(current_nav_state_.bg_);
optimizer.addVertex(v1_bg);
auto v1_ba = new VertexAccBias();
v1_ba->setId(7);
v1_ba->setEstimate(current_nav_state_.ba_);
optimizer.addVertex(v1_ba);
// imu factor
auto edge_inertial = new EdgeInertial(preinteg_, imu_init_.GetGravity());
edge_inertial->setVertex(0, v0_pose);
edge_inertial->setVertex(1, v0_vel);
edge_inertial->setVertex(2, v0_bg);
edge_inertial->setVertex(3, v0_ba);
edge_inertial->setVertex(4, v1_pose);
edge_inertial->setVertex(5, v1_vel);
auto *rk = new g2o::RobustKernelHuber();
rk->setDelta(200.0);
edge_inertial->setRobustKernel(rk);
optimizer.addEdge(edge_inertial);
// 零偏随机游走
auto *edge_gyro_rw = new EdgeGyroRW();
edge_gyro_rw->setVertex(0, v0_bg);
edge_gyro_rw->setVertex(1, v1_bg);
edge_gyro_rw->setInformation(options_.bg_rw_info_);
optimizer.addEdge(edge_gyro_rw);
auto *edge_acc_rw = new EdgeAccRW();
edge_acc_rw->setVertex(0, v0_ba);
edge_acc_rw->setVertex(1, v1_ba);
edge_acc_rw->setInformation(options_.ba_rw_info_);
optimizer.addEdge(edge_acc_rw);
// 上一帧pose, vel, bg, ba的先验
auto *edge_prior = new EdgePriorPoseNavState(last_nav_state_, prior_info_);
edge_prior->setVertex(0, v0_pose);
edge_prior->setVertex(1, v0_vel);
edge_prior->setVertex(2, v0_bg);
edge_prior->setVertex(3, v0_ba);
optimizer.addEdge(edge_prior);
/// 使用NDT的pose进行观测
auto *edge_ndt = new EdgeGNSS(v1_pose, ndt_pose_);
edge_ndt->setInformation(options_.ndt_info_);
optimizer.addEdge(edge_ndt);
if (options_.verbose_) {
LOG(INFO) << "last: " << last_nav_state_;
LOG(INFO) << "pred: " << current_nav_state_;
LOG(INFO) << "NDT: " << ndt_pose_.translation().transpose() << ","
<< ndt_pose_.so3().unit_quaternion().coeffs().transpose();
}
// 在优化过程中,将 i 时刻的bg和ba节点视为固定节点,不进行优化
v0_bg->setFixed(true);
v0_ba->setFixed(true);
// go
optimizer.setVerbose(options_.verbose_);
optimizer.initializeOptimization();
optimizer.optimize(20);
// get results
last_nav_state_.R_ = v0_pose->estimate().so3();
last_nav_state_.p_ = v0_pose->estimate().translation();
last_nav_state_.v_ = v0_vel->estimate();
last_nav_state_.bg_ = v0_bg->estimate();
last_nav_state_.ba_ = v0_ba->estimate();
current_nav_state_.R_ = v1_pose->estimate().so3();
current_nav_state_.p_ = v1_pose->estimate().translation();
current_nav_state_.v_ = v1_vel->estimate();
current_nav_state_.bg_ = v1_bg->estimate();
current_nav_state_.ba_ = v1_ba->estimate();
if (options_.verbose_) {
LOG(INFO) << "last changed to: " << last_nav_state_;
LOG(INFO) << "curr changed to: " << current_nav_state_;
LOG(INFO) << "preinteg chi2: " << edge_inertial->chi2() << ", err: " << edge_inertial->error().transpose();
LOG(INFO) << "prior chi2: " << edge_prior->chi2() << ", err: " << edge_prior->error().transpose();
LOG(INFO) << "ndt: " << edge_ndt->chi2() << "/" << edge_ndt->error().transpose();
}
/// 重置预积分
options_.preinteg_options_.init_bg_ = current_nav_state_.bg_;
options_.preinteg_options_.init_ba_ = current_nav_state_.ba_;
preinteg_ = std::make_shared<IMUPreintegration>(options_.preinteg_options_);
// gauss-newton 迭代中累加Hessian和error,计算dx类似。一共 5 种类型的边,在累加Hessian都要考虑上。
// 计算当前时刻先验
// 构建hessian
// 15x2,顺序:v0_pose, v0_vel, v0_bg, v0_ba, v1_pose, v1_vel, v1_bg, v1_ba
// 0 6 9 12 15 21 24 27
Eigen::Matrix<double, 30, 30> H;
H.setZero();
// ①添加 预积分因子的 Hessian 矩阵
H.block<24, 24>(0, 0) += edge_inertial->GetHessian();
// ②添加 陀螺仪零偏随机游走因子 的 Hessian 矩阵
Eigen::Matrix<double, 6, 6> Hgr = edge_gyro_rw->GetHessian();
// 行: bg1 列: bg1
H.block<3, 3>(9, 9) += Hgr.block<3, 3>(0, 0);
// 行: bg1 列: bg2
H.block<3, 3>(9, 24) += Hgr.block<3, 3>(0, 3);
// 行: bg2 列: bg1
H.block<3, 3>(24, 9) += Hgr.block<3, 3>(3, 0);
// 行: bg2 列: bg2
H.block<3, 3>(24, 24) += Hgr.block<3, 3>(3, 3);
// ③添加 加速度计零偏随机游走因子 的 Hessian 矩阵
Eigen::Matrix<double, 6, 6> Har = edge_acc_rw->GetHessian();
H.block<3, 3>(12, 12) += Har.block<3, 3>(0, 0);
H.block<3, 3>(12, 27) += Har.block<3, 3>(0, 3);
H.block<3, 3>(27, 12) += Har.block<3, 3>(3, 0);
H.block<3, 3>(27, 27) += Har.block<3, 3>(3, 3);
// ④添加 先验因子 的 Hessian 矩阵
H.block<15, 15>(0, 0) += edge_prior->GetHessian();
// ⑤添加 NDT 观测因子的 Hessian 矩阵
H.block<6, 6>(15, 15) += edge_ndt->GetHessian();
// 边缘化(利用 H 的稀疏性加速 HΔx=g 的求解的方法。视觉SLAM十四讲 p245)
// 边缘化(在本轮优化完成后,利用边缘化的方法,求出下一个关键帧位姿的协方差,作为下一轮优化的先验因子的信息矩阵使用。sad p245)
H = math::Marginalize(H, 0, 14);
prior_info_ = H.block<15, 15>(15, 15);
if (options_.verbose_) {
LOG(INFO) << "info trace: " << prior_info_.trace();
LOG(INFO) << "optimization done.";
}
NormalizeVelocity();
last_nav_state_ = current_nav_state_;
}4.6 边缘化
4.6.1 边缘化公式
对于 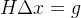

对线性方程组进行高斯消元,目标是消去右上角的 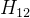
整理得:
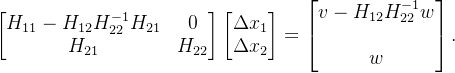
消元之后,方程组的第一行就变成和 

这样,就将求解 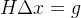





4.6.2 边缘化过程
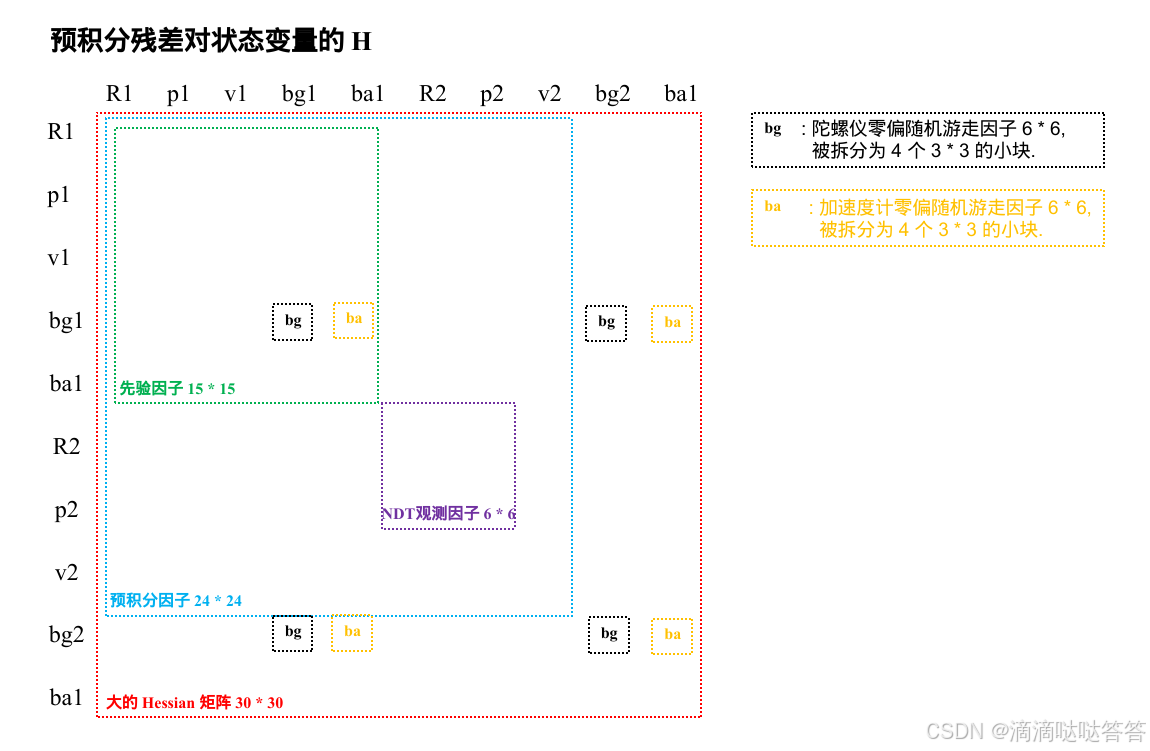
图优化完毕后,把 5 种因子(预积分因子、2个零偏随机游走因子、先验因子和NDT观测因子)的海塞 (Hessian) 矩阵按照顺序累加组合成一个大的 Hessian 矩阵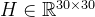
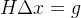
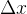
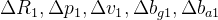
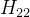
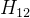

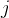
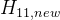
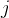

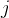
累加 5 种因子的 Hessian 矩阵一个大的 Hessian 矩阵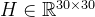
// gauss-newton 迭代中累加Hessian和error,计算dx类似。一共 5 种类型的边,在累加Hessian都要考虑上。
// 计算当前时刻先验
// 构建hessian
// 15x2,顺序:v0_pose, v0_vel, v0_bg, v0_ba, v1_pose, v1_vel, v1_bg, v1_ba
// 0 6 9 12 15 21 24 27
Eigen::Matrix<double, 30, 30> H;
H.setZero();
// ①添加 预积分因子的 Hessian 矩阵
H.block<24, 24>(0, 0) += edge_inertial->GetHessian();
// ②添加 陀螺仪零偏随机游走因子 的 Hessian 矩阵
Eigen::Matrix<double, 6, 6> Hgr = edge_gyro_rw->GetHessian();
// 行: bg1 列: bg1
H.block<3, 3>(9, 9) += Hgr.block<3, 3>(0, 0);
// 行: bg1 列: bg2
H.block<3, 3>(9, 24) += Hgr.block<3, 3>(0, 3);
// 行: bg2 列: bg1
H.block<3, 3>(24, 9) += Hgr.block<3, 3>(3, 0);
// 行: bg2 列: bg2
H.block<3, 3>(24, 24) += Hgr.block<3, 3>(3, 3);
// ③添加 加速度计零偏随机游走因子 的 Hessian 矩阵
Eigen::Matrix<double, 6, 6> Har = edge_acc_rw->GetHessian();
H.block<3, 3>(12, 12) += Har.block<3, 3>(0, 0);
H.block<3, 3>(12, 27) += Har.block<3, 3>(0, 3);
H.block<3, 3>(27, 12) += Har.block<3, 3>(3, 0);
H.block<3, 3>(27, 27) += Har.block<3, 3>(3, 3);
// ④添加 先验因子 的 Hessian 矩阵
H.block<15, 15>(0, 0) += edge_prior->GetHessian();
// ⑤添加 NDT 观测因子的 Hessian 矩阵
H.block<6, 6>(15, 15) += edge_ndt->GetHessian();
// 边缘化(利用 H 的稀疏性加速 HΔx=g 的求解的方法。视觉SLAM十四讲 p245)
// 边缘化(在本轮优化完成后,利用边缘化的方法,求出下一个关键帧位姿的协方差,作为下一轮优化的先验因子的信息矩阵使用。sad p245)
H = math::Marginalize(H, 0, 14);
prior_info_ = H.block<15, 15>(15, 15); 将 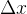
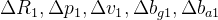
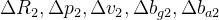
// 边缘化(利用 H 的稀疏性加速 HΔx=g 的求解的方法。视觉SLAM十四讲 p245)
// 边缘化(在本轮优化完成后,利用边缘化的方法,求出下一个关键帧位姿的协方差,作为下一轮优化的先验因子的信息矩阵使用。sad p245)
H = math::Marginalize(H, 0, 14);
prior_info_ = H.block<15, 15>(15, 15); 边缘化的目标如下,要将通过函数形参 start 和 end 选定的 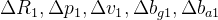
a | ab | ac a* | 0 | ac*
ba | b | bc --> 0 | 0 | 0
ca | cb | c ca* | 0 | c*- 1.通过函数形参 start 和 end 选定待边缘化的
增量范围(对应矩阵块 b);
- 2.将
移动到
的下方,即对应的 b 矩阵块也移动到矩阵 H 的右下角;
a | ab | ac a | ac | ab
ba | b | bc --> ca | c | cb
ca | cb | c ba | bc | b- 3.对 b 矩阵块进行奇异值分解求其伪逆,即
。
,
;
- 4.使用如下公式更新 H 矩阵;
注意:有于在这个部分后续不会使用 
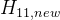
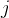

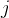
- 5.将更新后的 H 矩阵恢复为初始顺序。
a* | ac* | 0 a* | 0 | ac*
ca* | c* | 0 --> 0 | 0 | 0
0 | 0 | 0 ca* | 0 | c*具体代码如下:
/**
* 边缘化。视觉SLAM十四讲。p 249
* @param H
* @param start
* @param end
* @return
*/
inline Eigen::MatrixXd Marginalize(const Eigen::MatrixXd& H, const int& start, const int& end) {
// ① 通过函数形参 start 和 end 选定待边缘化的 Δx_(Scher) 增量范围(对应矩阵块 b)
// Goal
// a | ab | ac a* | 0 | ac*
// ba | b | bc --> 0 | 0 | 0
// ca | cb | c ca* | 0 | c*
// Size of block before block to marginalize
const int a = start;
// Size of block to marginalize
const int b = end - start + 1;
// Size of block after block to marginalize
const int c = H.cols() - (end + 1);
// ② 将 Δx_(Scher) 移动到 Δx 的下方,即对应的 b 矩阵块也移动到矩阵 H 的右下角
// Reorder as follows:
// a | ab | ac a | ac | ab
// ba | b | bc --> ca | c | cb
// ca | cb | c ba | bc | b
Eigen::MatrixXd Hn = Eigen::MatrixXd::Zero(H.rows(), H.cols());
// block函数:block(startRow, startCol, rows, cols);
if (a > 0) {
Hn.block(0, 0, a, a) = H.block(0, 0, a, a);
Hn.block(0, a + c, a, b) = H.block(0, a, a, b);
Hn.block(a + c, 0, b, a) = H.block(a, 0, b, a);
}
if (a > 0 && c > 0) {
Hn.block(0, a, a, c) = H.block(0, a + b, a, c);
Hn.block(a, 0, c, a) = H.block(a + b, 0, c, a);
}
if (c > 0) {
Hn.block(a, a, c, c) = H.block(a + b, a + b, c, c);
Hn.block(a, a + c, c, b) = H.block(a + b, a, c, b);
Hn.block(a + c, a, b, c) = H.block(a, a + b, b, c);
}
Hn.block(a + c, a + c, b, b) = H.block(a, a, b, b);
// ③ 对 b 矩阵块进行奇异值分解求其伪逆,即 H22^-1。A = U*Σ*V^T A^-1 = V*Σ^-1*U^T
// Perform marginalization (Schur complement)
Eigen::JacobiSVD<Eigen::MatrixXd> svd(Hn.block(a + c, a + c, b, b), Eigen::ComputeThinU | Eigen::ComputeThinV);
// 返回奇异值矩阵 Σ,即对角矩阵,其中每个对角元素都是 b 矩阵块 的奇异值。
Eigen::JacobiSVD<Eigen::MatrixXd>::SingularValuesType singularValues_inv = svd.singularValues();
// 计算 Σ^-1
for (int i = 0; i < b; ++i) {
if (singularValues_inv(i) > 1e-6) singularValues_inv(i) = 1.0 / singularValues_inv(i);
else
singularValues_inv(i) = 0;
}
// 使用奇异值分解法求 b 矩阵块的伪逆。A^-1 = V*Σ^-1*U^T
Eigen::MatrixXd invHb = svd.matrixV() * singularValues_inv.asDiagonal() * svd.matrixU().transpose();
// ④ 使用公式更新 H 矩阵
// H11 = H11 - H12 * H22^-1 * H21
// H12 = 0
// H21 = H21
// H22 = H22
Hn.block(0, 0, a + c, a + c) =
Hn.block(0, 0, a + c, a + c) - Hn.block(0, a + c, a + c, b) * invHb * Hn.block(a + c, 0, b, a + c);
Hn.block(a + c, a + c, b, b) = Eigen::MatrixXd::Zero(b, b);
Hn.block(0, a + c, a + c, b) = Eigen::MatrixXd::Zero(a + c, b);
Hn.block(a + c, 0, b, a + c) = Eigen::MatrixXd::Zero(b, a + c);
// ⑤将更新后的 H 矩阵恢复为初始顺序
// Inverse reorder
// a* | ac* | 0 a* | 0 | ac*
// ca* | c* | 0 --> 0 | 0 | 0
// 0 | 0 | 0 ca* | 0 | c*
Eigen::MatrixXd res = Eigen::MatrixXd::Zero(H.rows(), H.cols());
if (a > 0) {
res.block(0, 0, a, a) = Hn.block(0, 0, a, a);
res.block(0, a, a, b) = Hn.block(0, a + c, a, b);
res.block(a, 0, b, a) = Hn.block(a + c, 0, b, a);
}
if (a > 0 && c > 0) {
res.block(0, a + b, a, c) = Hn.block(0, a, a, c);
res.block(a + b, 0, c, a) = Hn.block(a, 0, c, a);
}
if (c > 0) {
res.block(a + b, a + b, c, c) = Hn.block(a, a, c, c);
res.block(a + b, a, c, b) = Hn.block(a, a + c, c, b);
res.block(a, a + b, b, c) = Hn.block(a + c, a, b, c);
}
res.block(a, a, b, b) = Hn.block(a + c, a + c, b, b);
return res;
}
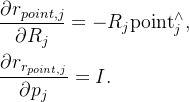
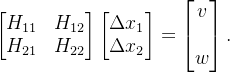
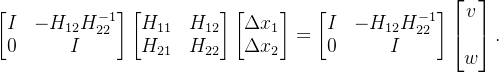
![[H_{11}-H_{12}H_{22}^{-1}H_{21}]\Delta x_1=v-H_{12}H_{22}^{-1}w](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJIXyU3QjExJTdELUhfJTdCMTIlN0RIXyU3QjIyJTdEJTVFJTdCLTElN0RIXyU3QjIxJTdEJTVEJTVDRGVsdGElMjB4XzElM0R2LUhfJTdCMTIlN0RIXyU3QjIyJTdEJTVFJTdCLTElN0R3)