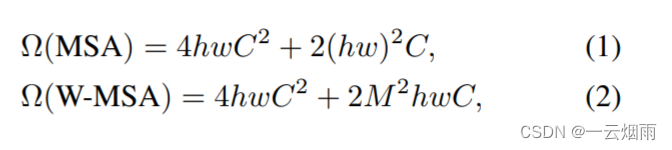《Swin Transformer: Hierarchical Vision Transformer using Shifted Windows》使用移动窗口的层级式视觉Transformer
前言
存在的问题:
Transformer模型从NLP领域移植到CV领域需要考虑的两个最具挑战性的问题是:1、一幅图像内通常包含多种尺度的实体,然而在NLP中却缺失尺度的概念,所以Transformer模型如何应用于下游任务(例如目标检测、分割等)成为研究热点;2、图像的分辨率较大,不适合作为Transformer模型的输入序列,虽然已经有相关的处理办法(例如将图像分割为patch、使用提取的特征图作为输入等),但如何将图像与Transformer模型进行完美契合仍是重点研究的方向。
创新点:
基于上述两点,提出了一种新的视觉Transformer,称为Swin Transformer,可用作通用计算机视觉的骨干架构。该架构通过将图像划分为不重叠的局部窗口(local windows),并在窗口内进行self-attention计算,同时经过移位(Shifted windows,Swin)之后还允许跨窗口连接(cross-window connection),从而带来更高的效率。这种分层架构具有在各种尺度上建模的灵活性,并且具有相对于图像大小的线性计算复杂度。
模型方法
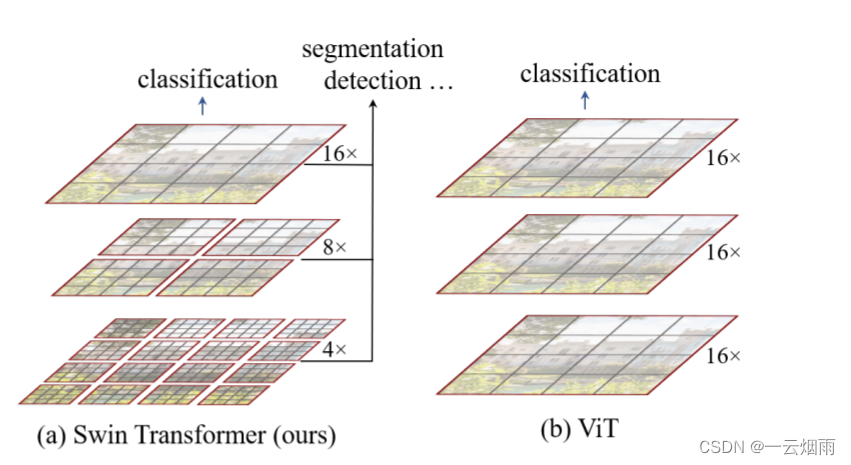
Swin Transformer模型与ViT模型的对比如下图所示:
ViT模型一直采用的是
16
×
16
16 \times 16
16×16的patch,每一层Transformer block所感受的尺寸均相同,相当于特征图的分辨率较低且保持不变(a single low resolution)。虽然ViT对全局执行自注意力机制进行全局建模,但是其对于多尺度的感知较弱。ViT的计算复杂度与图像的尺寸成平方(quadratic computation complexity)关系,当图像尺寸较大时,序列长度过长导致模型难以接受。
Swin Transformer模型计算复杂度与图像尺寸成线性增长关系(linear computation complexity)。一开始的采样率是4倍,经过类似于CNN的池化操作(merging image patches)后,将采样率提升至8倍、16倍,从而获得多尺度的特征信息,完成后续的处理任务(例如目标检测中的FPN,分割中的UNeT)。综上所述,Swin Transformer模型是可以作为图像分类和密集预测任务的通用主干( general-purpose backbone )。
移动窗口
上图中红色框表示中型计算单元的局部窗口,灰色小框表示最基本的元素单元,即一个
4
×
4
4 \times 4
4×4的小patch。在论文中,一个局部窗口中实际上包括
7
×
7
=
49
7 \times 7 = 49
7×7=49个小patch。
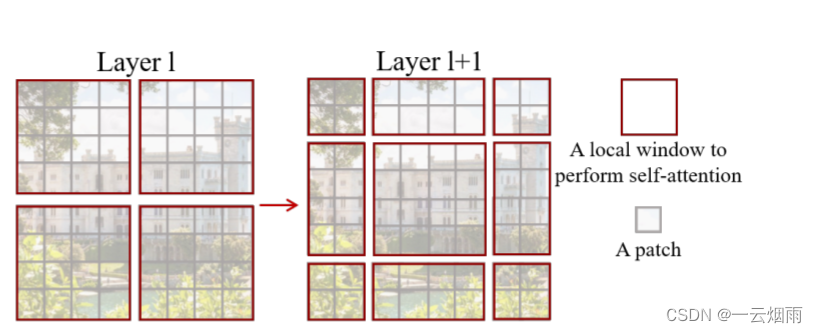
在第 l 层(左侧所示),采用常规的窗口划分方案,并在每个窗口内计算自注意力。 在下一层 l + 1(右)中,窗口分区发生了变化,从而产生了新窗口。 新窗口中的自注意力计算跨越了第 l 层中先前窗口的边界,提供了它们之间的连接。窗口的移动方式相当于,向右下方移动了两个patch。移动之后,窗口的数量变为9个。
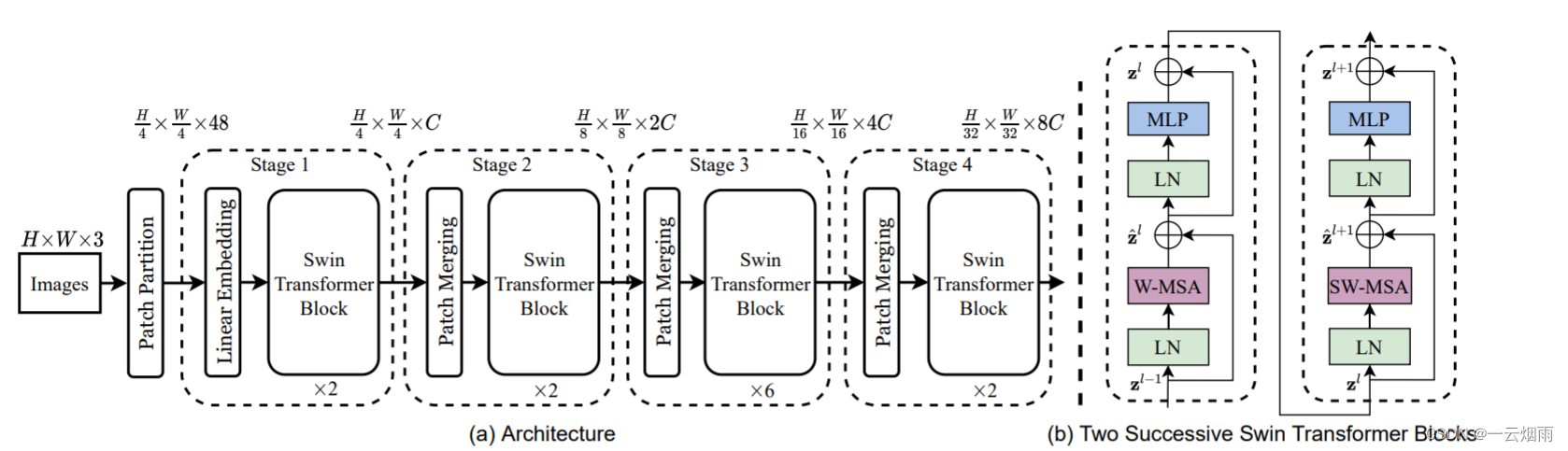
整体架构
- Patch Partition:先将输入图像划分为patch,以ImageNet图像的 224 × 224 224 \times 224 224×224为例,论文中划分为 4 × 4 4 \times 4 4×4的小patch,所以 H 4 × W 4 × 48 \frac{H}{4} \times \frac{W}{4} \times 48 4H×4W×48等于 56 × 56 × 48 56 \times 56 \times 48 56×56×48,48的由来是patch尺寸 4 × 4 4 \times 4 4×4再乘以3通道;
- Stage 1:Linear Embedding,特征尺寸变为 56 × 56 × 96 56 \times 56 \times 96 56×56×96;进入Swin Transformer Block时会将特征展成序列形式 3136 × 96 3136 \times 96 3136×96;基于窗口的自注意力机制使得序列长度为 7 × 7 = 49 7 \times 7 = 49 7×7=49,而非3136;
- Stage 2:Patch Merging,每次降采样是两倍,因此在行方向和列方向上,间隔2选取元素。
相当于通过空间上的维度转换为更多的通道数,间隔为2选取元素再拼接在一起的尺度为 H 2 × W 2 × 4 C \frac{H}{2} \times \frac{W}{2} \times 4C 2H×2W×4C,为了与CNN的池化操作更为一致(空间大小减半,通道数翻倍),所以再经过一次投影将尺度变为 H 2 × W 2 × 2 C \frac{H}{2} \times \frac{W}{2} \times 2C 2H×2W×2C;经过Patch Merging后的尺寸为 28 × 28 × 192 28 \times 28 \times 192 28×28×192; - Stage 3:经过Patch Merging后的尺寸为 14 × 14 × 384 14 \times 14 \times 384 14×14×384;
- Stage 4:经过Patch Merging后的尺寸为 7 × 7 × 768 7 \times 7 \times 768 7×7×768;
- 整体上并没有使用cls token,而是在 H 32 × W 32 × 8 C \frac{H}{32} \times \frac{W}{32} \times 8C 32H×32W×8C出来之后做全局平均池化,将 7 × 7 7 \times 7 7×7拉直得到 1 × 768 1 \times 768 1×768。整个模型采取层次化的设计,一共包含4个Stage,每个stage都会缩小输入特征图的分辨率,像CNN一样逐层扩大感受野。
论文中也估算了多头自注意力(MSA)和基于窗口的多头自注意力机制(W-MSA)的计算复杂度。
h
h
h、
w
w
w表示patch的个数,M表示一个窗口中patch的数量,以论文为例,
h
=
w
=
56
h=w=56
h=w=56,
M
=
7
M=7
M=7,C表示维度。
在B站李沐老师的讲解视频中,从第31分50秒开始有详细的推导过程。
提升移动窗口计算效率方法
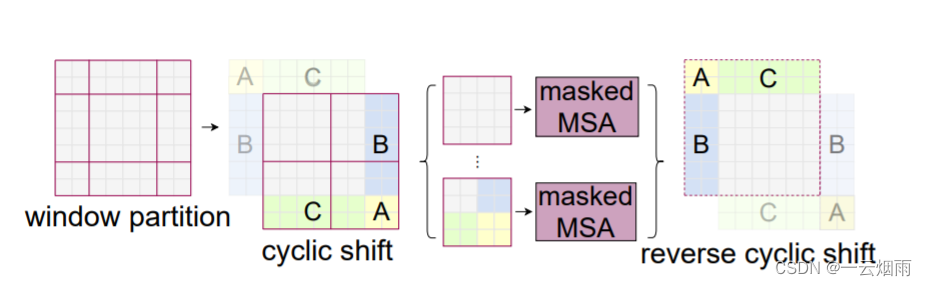
当移动窗口后,窗口数量会从4个增加至9个,无形中增加计算量。为了高效地批次处理,所以论文中提出,先将窗口执行循环移位(cyclic shift),用A、B、C补齐成为4个窗口;然后计算自注意力,并利用掩码(masked MSA)避免非相关特征之间的影响;最后再通过逆循环移位(reverse cyclic shift)将A、B、C还原回去。
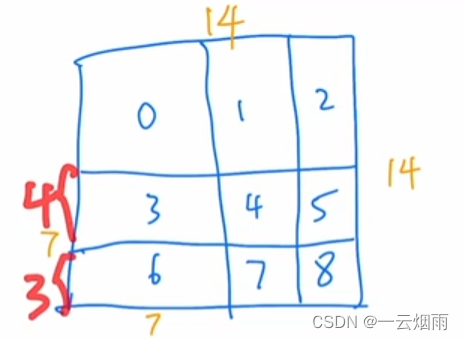
第一个图表示经过循环位移后示意图,8表示上图中的黄色A,2和5表示上图中的紫色B,6和7表示上图中的绿色C;0、1、3、4均为原图的特征信息。
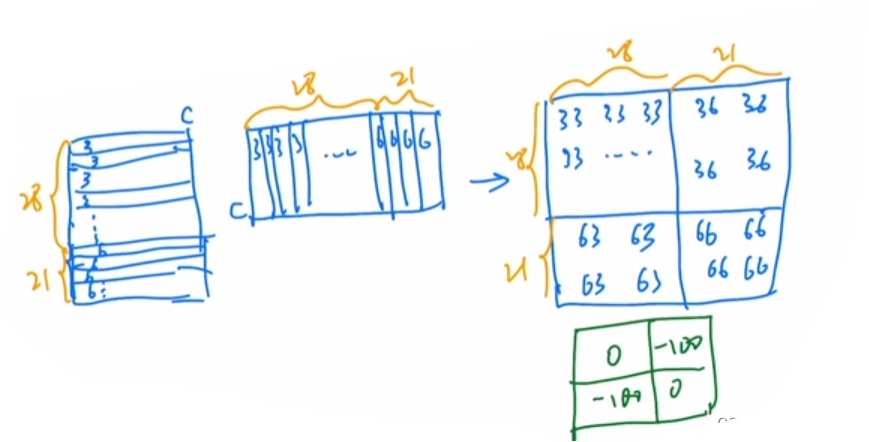
以3和6组成的新窗口为例,将其内部的元素排列起来,利用掩码执行自注意力的操作过程示意图:
- 左侧第一个图表示将窗口内的元素排列起来,前28个是元素属于3号,后21个属于6号;两者的维度均为C;
- 第二个图表示将左侧序列进行转置,以便求其自注意力;
- 最右侧的图表示前两者做矩阵乘法,首先得到左上角 28 × 28 28 \times 28 28×28大小的3号元素与3号元素的乘积,是需要的3号自注意力;再得到 28 × 21 28 \times 21 28×21大小的3号元素与6号元素的乘积,然而3号与6号之间没有相关性,实际上并不应该做自注意力;其次得到的 21 × 28 21 \times 28 21×28大小的6号元素与3号元素的乘积也是如此;最后得到的 21 × 21 21 \times 21 21×21大小的6号元素与6号元素的乘积是所需要的6号自注意力;
- 所以设计了绿色的掩码模板,其左上和右下两部分的模板值为0,右上和左下两部分的模板值为很大的负数;当模板与矩阵乘法结果相加再经过softmax后,右上和左下两部分的结果趋近于0,起到了掩码的作用,使得两个不相关的窗口没有产生影响。
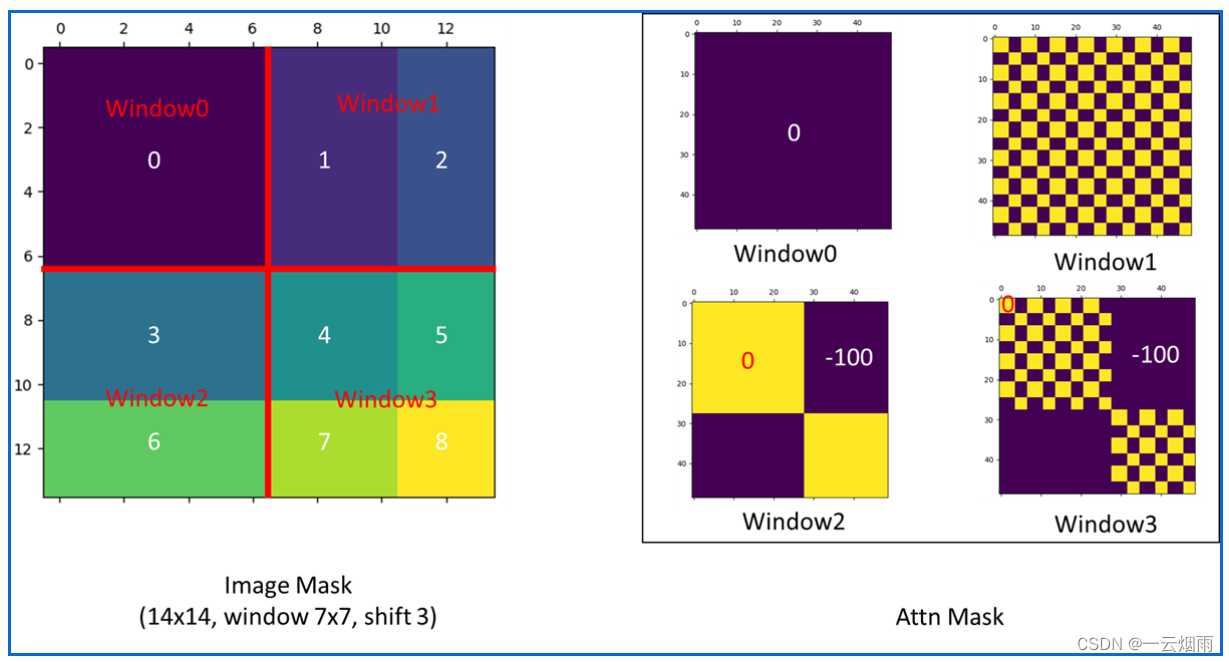
- 整体上4个窗口的掩码格式如下所示:
参考
- 代码复现:https://zhuanlan.zhihu.com/p/367111046
- 论文源址:https://arxiv.org/pdf/2103.14030.pdf