Bootstrap

数据结构--图（C++）

前言：图的知识点整理，欢迎评论交流。

数据结构--图（C++）

图的基本概念

图的定义，图由顶点集V和边集E组成，记为G=(V,E),其中V={v1,v2,v3,……，v（n）}，E={(u,v)|u∈V，v∈V}。
图(graph)、顶点(vertex)、边(dege)
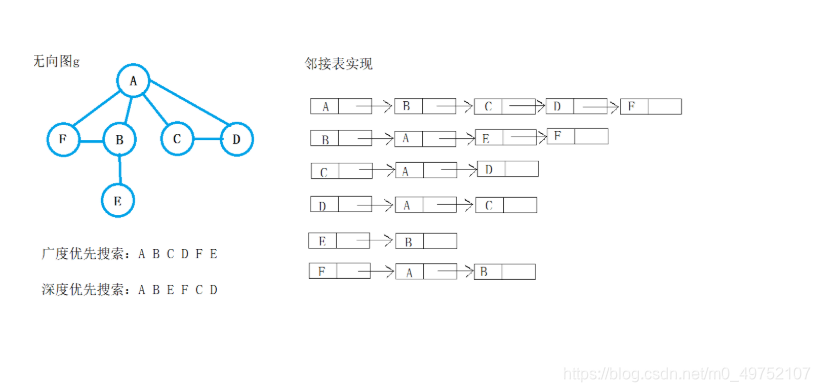
1.无向图、有向图及混合图
若E为无向边(undirected edge),则图G为无向图(undigraph)
若E为有向边(directed edge),则图G为有向图(digraph)
若E同时包含无向边和有向边,则图G为混合图(mixed graph)
2.简单图，不含任何自环(self-loop)的图称作简单图(simple graph)
3.连通图和连通分量
若图G中任意两个顶点都是连通的，则称图G为连通图。
无向图中的极大连通子图称为连通分量。
4.强连通图和强连通分量
有向图中，若从顶点v到顶点w和从顶点w到顶点v之间都有路径，则称这两个顶点是强连通的。
若图中任意一对顶点都是强连通的，则称此图为强连通图。
有向图中的极大强连通子图称为有向图的强连通分量。
5.顶点的度、入度和出度
无向图中，与顶点v关联的边数，称作v的度数(degree)，记作deg(v)。
有向图中，顶点的出边总数称为出度(out-degree),记作outdeg（v)，入边总数称为入度(in-degree),记作indeg(v)。
6.路径、路径长度和回路
顶点v1到顶点v3之间的一条路径是指顶点序列v1,v2,v3。
路径上边的数目称为路径长度。
第一个顶点和最后一个顶点相同的路径称为回路或环。
7.简单路径、简单回路
在路径序列中，顶点不重复出现的路径称为简单路径。
除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路
8.带权网络
各边均带有权重的图，称为带权图(weighted graph)或带权网络(weighted network)。

图结构的存储

邻接矩阵

邻接矩阵的存储结构

用一个一维数组vertices[]存储顶点信息，用一个二维数组edge[]存储边的信息，变量vexnum存储顶点数，变量edgenum存储边数。
代码片.

struct MGraph									//邻接矩阵
{
	VertexType Vertices[MaxVertexNum];
	EdgeType Edge[MaxVertexNum][MaxVertexNum];
	int vexnum;
	int edgenum;
};

创建一个邻接矩阵图

在这里插入图片描述

代码片.

#include<iostream>__msvc_all_public_headers.hpp
#include<queue>
using namespace std;
const int MaxVertexNum = 100;
const int MaxWeight = 1000;
const int inf = 100000;

typedef char VertexType;
typedef int EdgeType;


struct MGraph									//邻接矩阵
{
	VertexType Vertices[MaxVertexNum];
	EdgeType Edge[MaxVertexNum][MaxVertexNum];
	int vexnum;
	int edgenum;
};

		//初始化
void init(MGraph &G)
{
	for (int i = 0;i < MaxVertexNum;i++)
		G.Vertices[i] = 0;
	for(int i=0;i<MaxVertexNum;i++)
		for(int j=0;j<MaxVertexNum;j++)
			G.Edge[i][j] = inf;
	G.vexnum = 0;
	G.edgenum = 0;
}

		//得到顶点位置
int getVertexPos(MGraph &G, VertexType vertex)
{
	for (int i = 0;i < MaxVertexNum;i++)
		if (G.Vertices[i] == vertex) return i;
	return false;
}


		//插入顶点
bool insertVertex(MGraph &G, VertexType vertex)
{
	if (G.vexnum == MaxVertexNum) return false;	//顶点表已满，返回false
	G.Vertices[G.vexnum++] = vertex;
	return true;
}

		//插入边
bool insertEdge(MGraph &G, VertexType vertex1, VertexType vertex2, EdgeType weight)
{
	int v1 = getVertexPos(G, vertex1);
	int v2 = getVertexPos(G, vertex2);
	if (v1 > -1 && v1<MaxVertexNum && v2>-1 && v2 < MaxVertexNum)
	{
		G.Edge[v1][v2] =G.Edge[v2][v1]= weight;		//无向图
		G.edgenum++;
		return true;
	}
	return false;
}


void test01()
{
	char A = 'A', B = 'B', C = 'C', D = 'D', E = 'E', F = 'F';
	MGraph g;
	init(g);
	insertVertex(g, A);
	insertVertex(g, B);
	insertVertex(g, C);
	insertVertex(g, D);
	insertVertex(g, E);
	insertVertex(g, F);
	insertEdge(g, A, B, 1);
	insertEdge(g, A, C, 1);
	insertEdge(g, A, D, 1);
	insertEdge(g, A, F, 1);
	insertEdge(g, B, E, 1);
	insertEdge(g, B, F, 1);
	insertEdge(g, C, D, 1);
}

int main()
{
	test01();
	return 0;
}

邻接表

邻接表的存储结构

代码片.

const int MaxVertexNum = 100;
typedef char VertexType;

//边表结点
struct EdgeNode
{
	int adjvex;
	EdgeNode* next;
};

//顶点表结点
typedef struct VexNode
{
	VertexType data;
	EdgeNode* first;
}VexNode,AdjList[MaxVertexNum];

//邻接表
struct ALGraph 
{
	AdjList vertices;
	int vexnum;
	int edgenum;
};

创建一个邻接表

邻接表

代码片.

#include<iostream>__msvc_all_public_headers.hpp
#include<queue>accountssettingspaneinterop.h
using namespace std;

const int MaxVertexNum = 100;
typedef char VertexType;

//边表结点
struct EdgeNode
{
	int adjvex;
	EdgeNode* next;
};

//顶点表结点
typedef struct VexNode
{
	VertexType data;
	EdgeNode* first;
}VexNode,AdjList[MaxVertexNum];

//邻接表
struct ALGraph 
{
	AdjList vertices;
	int vexnum;
	int edgenum;
};

//初始化
void init(ALGraph& G)
{
	for (int i = 0;i < MaxVertexNum;i++)
	{
		G.vertices[i].data = 0;
		G.vertices[i].first = 0;
	}
	G.vexnum = 0;
	G.edgenum = 0;
}

//顶点位置
int getVertexPos(ALGraph G, VertexType vertex)
{
	for (int i = 0;i < G.vexnum;i++)
		if (G.vertices[i].data ==vertex)
			return i;
	return -1;
}

//插入顶点
bool insertVertex(ALGraph& G, VertexType vertex)
{
	if (G.vexnum == MaxVertexNum) return false;
	G.vertices[G.vexnum++].data = vertex;
	return true;
}

//插入边
void insertEdge(ALGraph& G, VertexType vertex1, VertexType vertex2)
{
	int v1 = getVertexPos(G, vertex1);
	int v2 = getVertexPos(G, vertex2);
	EdgeNode* enode = new EdgeNode;
	enode->adjvex =v2;
	enode->next = NULL;
	if (G.vertices[v1].first == NULL)
		G.vertices[v1].first = enode;
	else
	{
		EdgeNode* p;
		p = G.vertices[v1].first;
		while (p->next != NULL)
			p = p->next;
		p->next = enode;
	}

	EdgeNode* enode2 = new EdgeNode;
	enode2->adjvex = v1;
	enode2->next = NULL;
	if (G.vertices[v2].first == NULL)
		G.vertices[v2].first = enode2;
	else
	{
		EdgeNode* p;
		p = G.vertices[v2].first;
		while (p->next != NULL)
			p = p->next;
		p->next = enode2;
	}
	G.edgenum++;
}

void test()
{
	char A = 'A', B = 'B', C = 'C', D = 'D', E = 'E', F = 'F';
	ALGraph g;
	init(g);
	insertVertex(g, A);
	insertVertex(g, B);
	insertVertex(g, C);
	insertVertex(g, D);
	insertVertex(g, E);
	insertVertex(g, F);
	insertEdge(g, A, B);
	insertEdge(g, A, C);
	insertEdge(g, A, D);
	insertEdge(g, A, F);
	insertEdge(g, B, E);
	insertEdge(g, B, F);
	insertEdge(g, C, D);
}


int main()
{
	test();
	return 0;
}

十字链表

十字链表是有向图的一种链式存储结构。
参考：https://blog.csdn.net/bible_reader/article/details/71214096

链接多重表

链接多重表是无向图的一种链式存储结构。
参考：https://blog.csdn.net/bible_reader/article/details/71250117

图的遍历

邻接矩阵的广度优先搜索

代码片.


queue<int> Q;					//广度优先遍历
bool visited[MaxVertexNum];

void BFS(MGraph G, int v)
{
	cout << G.Vertices[v] << endl;		//visit(v)
	visited[v] = true;
	Q.push(v);
	while (!Q.empty())
	{
		Q.pop();
		for (int w = FirstNeighbor(G, v);w >= 0;w = NextNeighbor(G, v, w))
			if (!visited[w])
			{
				cout << G.Vertices[w] << endl;
				visited[w] = true;
				Q.push(w);
			}
	}
}

void BFStraverse(MGraph G)
{
	for (int i = 0;i < G.vexnum;i++)
		visited[i] = false;
	for (int i = 0;i < G.vexnum;i++)
	{
		if (!visited[i])
			BFS(G, i);
	}
}

遍历结果
在这里插入图片描述

邻接矩阵的深度优先搜索

代码片.

void DFS(MGraph G, int v)
{
	cout << G.Vertices[v] << endl;
	visited[v] = true;
	for (int w = FirstNeighbor(G, v);w >= 0;w = NextNeighbor(G, v, w))
		if (!visited[w])
			DFS(G, w);
}

void DFStraverse(MGraph G)
{
	for (int i = 0;i < G.vexnum;i++)
		visited[i] = false;
	for (int i = 0;i < G.vexnum;i++)
		if (!visited[i])
			DFS(G, i);
}

遍历结果
在这里插入图片描述

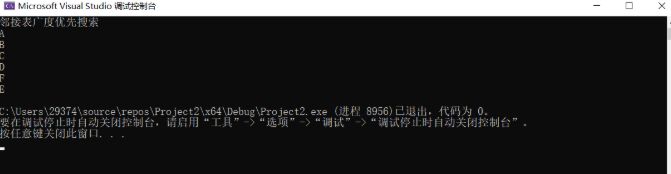
邻接表的广度优先搜索

代码片.

bool visited[MaxVertexNum];  //标记数组
//广度优先搜索
queue<int> Q;
void BFS(ALGraph G, int v)
{
	cout << G.vertices[v].data << endl;
	visited[v] = true;
	Q.push(v);
	while (!Q.empty())
	{
		Q.pop();
		for (EdgeNode* p = G.vertices[v].first;p > 0;p = p->next)
			if (!visited[p->adjvex])
			{
				cout << G.vertices[p->adjvex].data << endl;
				visited[p->adjvex] = true;
				Q.push(p->adjvex);
			}
	}
}

void BFStraverse(ALGraph G)
{
	for (int i = 0;i < G.vexnum;i++)
		visited[i] = 0;
	for (int i = 0;i < G.vexnum;i++)
		if (!visited[i])
			BFS(G, i);
}

遍历结果
地方

邻接表的深度优先搜索

代码片.

bool visited[MaxVertexNum];  //标记数组
//深度优先搜索
void DFS(ALGraph G, int v)
{
	cout << G.vertices[v].data << endl;
	visited[v] = true;
	for (EdgeNode* p = G.vertices[v].first;p > 0;p = p->next)
		if (!visited[p->adjvex])
			DFS(G, p->adjvex);
}

void DFStraverse(ALGraph G)
{
	for (int i = 0;i < G.vexnum;i++)
		visited[i] = 0;
	for (int i = 0;i < G.vexnum;i++)
		if (!visited[i])
			DFS(G, i);
}

遍历结果
在这里插入图片描述

图的应用

最小生成树

生成树，一个连通图的生成树是图的极小连通子图，它包含图中的所有顶点，并且只含尽可能少的边。这意味着对于生成树来说，若砍去它的一条边，则会使生成树变成非连通图；若给它增加一条边，则会形成图中的一条回路。
最小生成树，带权连通无向图G=(V,E)中，所有生成树中权值最小的那棵生成树，称为G的最小生成树（Minimum Spanning Tree，MST）。
性质
(1).最小生成树不是唯一的，即最小生成树的树形不唯一。
(2).最小生成树的边的权值之和总是唯一的，而且是最小的。
(3).最小生成树的边数为顶点数减一。
参考：最小生成树的动画演示https://www.bilibili.com/video/BV1Eb41177d1/
在这里插入图片描述

1.Prim算法

代码片.

struct MST									//最小生成树
{
	VertexType Vertices[MaxVertexNum];  //顶点集
	EdgeType Edge[MaxVertexNum][MaxVertexNum];//边集
	int vexnum;//顶点数
	int edgenum;//边数
	EdgeType lowcost[MaxVertexNum];//权值表
	EdgeType weight;//树的权值
};


void initMST(MST &T)  //初始化
{
	for (int i = 0;i < MaxVertexNum;i++)  
	{
		T.Vertices[i] = 0;
		T.lowcost[i] =0;
	}
	for (int i = 0;i < MaxVertexNum;i++)
		for (int j = 0;j < MaxVertexNum;j++)
			T.Edge[i][j] = 0;
	T.edgenum = 0;
	T.vexnum = 0;
	T.weight = 0;
}



int Min(int a[], int n)//数组中最小值的下标
{
	int min = inf;
	int v=0;
	for (int i = 0;i < n;i++)
		if (a[i] != 0 && a[i] < min)
		{
			min = a[i];
			v = i;
		}
	return v;
}




void Prim(MGraph G, MST &T)
{
	int v0= 0;	//从顶点v0开始
	int parent[MaxVertexNum];//标记数组，记录边尾节点的边头节点
	T.Vertices[v0] = G.Vertices[v0];//将第一个顶点加入T中
	T.vexnum++;		//T的顶点数加一
	for (int i = 1;i < G.vexnum;i++)
	{
		T.lowcost[i] = G.Edge[v0][i];	//边(v0，其他顶点)的权值表
		parent[i] = v0;
	}
	
	while (T.vexnum != G.vexnum)
	{
		int Vtail = Min(T.lowcost, G.vexnum);//边(Vhead，其他顶点)权值最小的边尾节点Vtail
		int Vhead= parent[Vtail];		//边(Vhead,Vtail)，边尾Vtail，边头Vhead
		T.Edge[Vhead][Vtail]=T.Edge[Vtail][Vhead] = G.Edge[Vhead][Vtail];//边归入树T中
		T.Vertices[Vtail] = G.Vertices[Vtail];//顶点归入树T中
		T.weight += T.Edge[Vhead][Vtail];//权值和
		T.vexnum++;//顶点加一
		T.edgenum++;//边加一
		for (int i = 0;i < G.vexnum;i++)//更新权值表
		{
			if (G.Edge[Vtail][i] > 0 && G.Edge[Vtail][i] < T.lowcost[i])
			{
				T.lowcost[i] = G.Edge[Vtail][i];//更新了(Vtail,i)的权值
				parent[i] = Vtail;//边尾Vtail的边头节点i
			}
		}
		T.lowcost[Vtail] = 0;//已记录的权值归零
	}
}

2.Kruskal算法

代码片.

//边
struct Edge
{
	int head, tail, weight;//边的头节点、尾节点和权值
};
//边集中插入边
void insEdge(MGraph G, Edge *edge)
{
	int n = 0;
	for (int i = 0;i < G.edgenum;i++)
		for (int j = i+1;j < G.edgenum;j++)
			if (G.Edge[i][j] !=inf)
			{
				edge[n].head = getVertexPos(G,G.Vertices[i]);
				edge[n].tail = getVertexPos(G, G.Vertices[j]);
				edge[n].weight = G.Edge[i][j];
				n++;
			}
}

//并查集
int Fa[MaxVertexNum];
void initFa(int *a,int n)
{
	for (int i = 0;i < n;i++)
		a[i] = i;
}

bool cmp(Edge& a, Edge& b) 
{
	return a.weight <= b.weight;
}


int findFa(int x)
{
	if (Fa[x] != x) {
		Fa[x] = findFa(Fa[x]); //找到并赋值，路径压缩
	}
	return Fa[x];
}


void Kruskal(MGraph G, MST& T)
{
	for (int i = 0;i < G.vexnum;i++)//顶点赋值
		T.Vertices[i] = G.Vertices[i];
	T.vexnum = G.vexnum;//顶点数赋值
	Edge edge[MaxVertexNum];//边集
	insEdge(G, edge);//插入边
	sort(edge, edge + G.edgenum, cmp);//边排序
	initFa(Fa, G.edgenum);
	for (int i = 0;i < G.edgenum;i++)//向T中依次添加边
		if (findFa(edge[i].head) != findFa(edge[i].tail))
		{
			int head = edge[i].head;
			int tail = edge[i].tail;
			T.Edge[head][tail] = T.Edge[tail][head] = edge[i].weight;
			T.edgenum++;
			T.weight += edge[i].weight;
			Fa[findFa(edge[i].tail)] = findFa(edge[i].head);
		}
}

完整代码

#include<iostream>__msvc_all_public_headers.hpp
#include<algorithm>__msvc_all_public_headers.hpp
using namespace std;
const int MaxVertexNum =100;
const int MaxWeight = 1000;
const int inf = 100000;
typedef char VertexType ;
typedef int EdgeType ;

struct MGraph									//邻接矩阵
{
	VertexType Vertices[MaxVertexNum];
	EdgeType Edge[MaxVertexNum][MaxVertexNum];
	int vexnum;
	int edgenum;
};

		//初始化
void init(MGraph& G)
{
	for (int i = 0;i < MaxVertexNum;i++)
		G.Vertices[i] = 0;
	for (int i = 0;i < MaxVertexNum;i++)
		for (int j = 0;j < MaxVertexNum;j++)
			G.Edge[i][j] = inf;
	G.vexnum = 0;
	G.edgenum = 0;
}

		//得到顶点位置
int getVertexPos(MGraph& G, VertexType vertex)
{
	for (int i = 0;i < MaxVertexNum;i++)
		if (G.Vertices[i] == vertex) return i;
	return false;
}


		//插入顶点
bool insertVertex(MGraph& G, VertexType vertex)
{
	if (G.vexnum == MaxVertexNum) return false;	//顶点表已满，返回false
	G.Vertices[G.vexnum++] = vertex;
	return true;
}

		//插入边
bool insertEdge(MGraph& G, VertexType vertex1, VertexType vertex2, EdgeType weight)
{
	int v1 = getVertexPos(G, vertex1);
	int v2 = getVertexPos(G, vertex2);
	if (v1 > -1 && v1<MaxVertexNum && v2>-1 && v2 < MaxVertexNum)
	{
		G.Edge[v1][v2] = G.Edge[v2][v1] = weight;		//无向图
		G.edgenum++;
		return true;
	}
	return false;
}




struct MST									//最小生成树
{
	VertexType Vertices[MaxVertexNum];  //顶点集
	EdgeType Edge[MaxVertexNum][MaxVertexNum];//边集
	int vexnum;//顶点数
	int edgenum;//边数
	EdgeType lowcost[MaxVertexNum];//权值表
	EdgeType weight;//树的权值
};




void initMST(MST &T)  //初始化
{
	for (int i = 0;i < MaxVertexNum;i++)  
	{
		T.Vertices[i] = 0;
		T.lowcost[i] =0;
	}
	for (int i = 0;i < MaxVertexNum;i++)
		for (int j = 0;j < MaxVertexNum;j++)
			T.Edge[i][j] = 0;
	T.edgenum = 0;
	T.vexnum = 0;
	T.weight = 0;
}



int Min(int a[], int n)//数组中最小值的下标
{
	int min = inf;
	int v=0;
	for (int i = 0;i < n;i++)
		if (a[i] != 0 && a[i] < min)
		{
			min = a[i];
			v = i;
		}
	return v;
}




void Prim(MGraph G, MST &T)
{
	int v0= 0;	//从顶点v0开始
	int parent[MaxVertexNum];//标记数组，记录边尾节点的边头节点
	T.Vertices[v0] = G.Vertices[v0];//将第一个顶点加入T中
	T.vexnum++;		//T的顶点数加一
	for (int i = 1;i < G.vexnum;i++)
	{
		T.lowcost[i] = G.Edge[v0][i];	//边(v0，其他顶点)的权值表
		parent[i] = v0;
	}
	
	while (T.vexnum != G.vexnum)
	{
		int Vtail = Min(T.lowcost, G.vexnum);//边(Vhead，其他顶点)权值最小的边尾节点Vtail
		int Vhead= parent[Vtail];		//边(Vhead,Vtail)，边尾Vtail，边头Vhead
		T.Edge[Vhead][Vtail]=T.Edge[Vtail][Vhead] = G.Edge[Vhead][Vtail];//边归入树T中
		T.Vertices[Vtail] = G.Vertices[Vtail];//顶点归入树T中
		T.weight += T.Edge[Vhead][Vtail];//权值和
		T.vexnum++;//顶点加一
		T.edgenum++;//边加一
		for (int i = 0;i < G.vexnum;i++)//更新权值表
		{
			if (G.Edge[Vtail][i] > 0 && G.Edge[Vtail][i] < T.lowcost[i])
			{
				T.lowcost[i] = G.Edge[Vtail][i];//更新了(Vtail,i)的权值
				parent[i] = Vtail;//边尾Vtail的边头节点i
			}
		}
		T.lowcost[Vtail] = 0;//已记录的权值归零
	}
}

    
//边
struct Edge
{
	int head, tail, weight;//边的头节点、尾节点和权值
};
//边集中插入边
void insEdge(MGraph G, Edge *edge)
{
	int n = 0;
	for (int i = 0;i < G.edgenum;i++)
		for (int j = i+1;j < G.edgenum;j++)
			if (G.Edge[i][j] !=inf)
			{
				edge[n].head = getVertexPos(G,G.Vertices[i]);
				edge[n].tail = getVertexPos(G, G.Vertices[j]);
				edge[n].weight = G.Edge[i][j];
				n++;
			}
}

//并查集
int Fa[MaxVertexNum];
void initFa(int *a,int n)
{
	for (int i = 0;i < n;i++)
		a[i] = i;
}

bool cmp(Edge& a, Edge& b) 
{
	return a.weight <= b.weight;
}


int findFa(int x)
{
	if (Fa[x] != x) {
		Fa[x] = findFa(Fa[x]); //找到并赋值，路径压缩
	}
	return Fa[x];
}


void Kruskal(MGraph G, MST& T)
{
	for (int i = 0;i < G.vexnum;i++)//顶点赋值
		T.Vertices[i] = G.Vertices[i];
	T.vexnum = G.vexnum;//顶点数赋值
	Edge edge[MaxVertexNum];//边集
	insEdge(G, edge);//插入边
	sort(edge, edge + G.edgenum, cmp);//边排序
	initFa(Fa, G.edgenum);
	for (int i = 0;i < G.edgenum;i++)//向T中依次添加边
		if (findFa(edge[i].head) != findFa(edge[i].tail))
		{
			int head = edge[i].head;
			int tail = edge[i].tail;
			T.Edge[head][tail] = T.Edge[tail][head] = edge[i].weight;
			T.edgenum++;
			T.weight += edge[i].weight;
			Fa[findFa(edge[i].tail)] = findFa(edge[i].head);
		}
}

void test01()
{
	char A = 'A', B = 'B', C = 'C', D = 'D', E = 'E', F = 'F';
	MGraph g;
	init(g);
	insertVertex(g, A);
	insertVertex(g, B);
	insertVertex(g, C);
	insertVertex(g, D);
	insertVertex(g, E);
	insertVertex(g, F);
	insertEdge(g, A, B, 4);
	insertEdge(g, A, C, 1);
	insertEdge(g, A, D, 6);
	insertEdge(g, A, F, 3);
	insertEdge(g, B, E, 9);
	insertEdge(g, B, F, 2);
	insertEdge(g, C, D, 5);
	MST t;
	initMST(t);//初始化
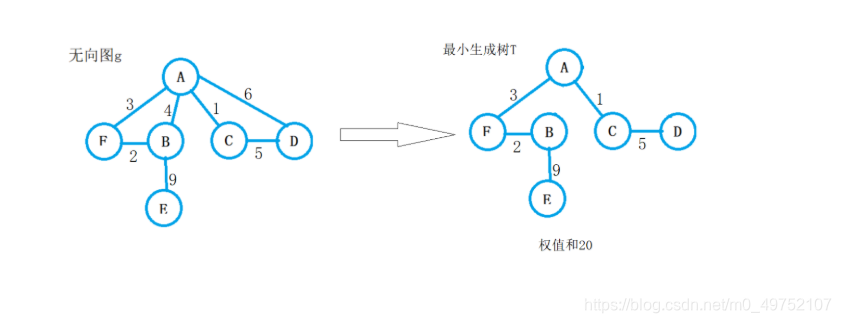
	Prim(g, t);
	cout << "Prim算法：" << endl;
	for (int i = 0;i < t.vexnum;i++)//打印边及权值
		for (int j = i + 1;j < t.vexnum;j++)
			if (t.Edge[i][j] != 0)
				cout << t.Vertices[i] << t.Vertices[j] << t.Edge[i][j] << endl;
	cout <<"权值和 "<<t.weight << endl;
	initMST(t);
	Kruskal(g, t);
	cout << "Kruskal算法：" << endl;
	for (int i = 0;i < t.vexnum;i++)//打印边及权值
		for (int j = i + 1;j < t.vexnum;j++)
			if (t.Edge[i][j] != 0)
				cout << t.Vertices[i] << t.Vertices[j] << t.Edge[i][j] << endl;
	cout << "权值和 " << t.weight << endl;
	
}




int main()
{
	test01();
	return 0;
}

运行结果

在这里插入图片描述

最短路径

最短路径，图是带权图时，把从一个顶点v0到图中其余任意一个顶点vi的一条路径所经过边上的权值之和，定义为该路径的带权路径长度，把带权路径长度最短的那条路径称为最短路径。

在这里插入图片描述

1.Dijkstra算法

代码片

//最短路径
struct DijkstraPath
{
	VertexType Vertices[MaxVertexNum];//顶点集
	int vexnum;//顶点数
	int visited[MaxVertexNum];//标记
	int	dist[MaxVertexNum];//距离
	int	path[MaxVertexNum];//路径
};
void initSP(DijkstraPath& P)//初始化
{
	for (int i = 0;i < MaxVertexNum;i++)
	{
		P.visited[i] = 0;
		P.dist[i] = 0;
		P.path[i] = 0;
	}
}

int Min(DijkstraPath &P,int n)//P.dist[]最小值的下标
{
	int min = inf;
	int v = 0;
	for (int i = 0;i < n;i++)
		if (!P.visited[i]&& P.dist[i] < min)
		{
			min = P.dist[i];
			v = i;
		}
	return v;
}



void Dijkstra(MGraph G,DijkstraPath &P)
{
	int v0 = 0;
	for (int i = 0;i < G.vexnum;i++)//赋值
	{
		P.Vertices[i] = G.Vertices[i];
		P.dist[i] = G.Edge[v0][i];	//顶点到其他顶点的权值
	}
	P.vexnum = G.vexnum;
	P.visited[v0] = 1;
	for (int i = 0;i < P.vexnum;i++)
	{
		int next = Min(P,G.vexnum);//边(Vhead，其他顶点)权值最小的边尾节点next
		P.visited[next] = 1;
		for (int i = 0;i < P.vexnum;i++)
		{
			if ((G.Edge[next][i] + P.dist[next]) < P.dist[i] && !P.visited[i])
			{
				P.dist[i] = G.Edge[next][i] + P.dist[next];
				P.path[i] = next;//记录路径
			}
		}
	}
}

//打印输出

void printP(DijkstraPath P, char x)//从顶点到x的最短路径
{
	stack<int> s;
	int tail=0,in=0;
	P.path[0] =inf;
	tail=in = getVertexPos(P.Vertices, x);//x的顶点序号
	while(in!=inf)//入栈
	{
		s.push(in);
		in = P.path[in];
	}
	cout << "Dijkstra算法"<<endl;
	cout << P.Vertices[0] << "到" << P.Vertices[tail] << "最短路径: ";
	while(!s.empty())//出栈
	{
		int out=s.top() ;
			cout << P.Vertices[out] << " ";
		s.pop();
	}
	cout << "权值：" << P.dist[tail] << endl;
}

2.Floyd算法

代码片


struct FloydPath
{
	VertexType Vertices[MaxVertexNum];//顶点集
	int vexnum;//顶点数
	int dist[MaxVertexNum][MaxVertexNum];
	int path[MaxVertexNum][MaxVertexNum];
};

void initFP(MGraph G, FloydPath &F)
{
	for (int row = 0;row < G.vexnum;row++)
		for (int col = 0;col < G.vexnum;col++)
		{
			F.dist[row][col] = G.Edge[row][col];
			F.path[row][col] = col;
		}
	for (int i = 0;i < G.vexnum;i++)//赋值
		F.Vertices[i] = G.Vertices[i];
	F.vexnum = G.vexnum;
}

void Floyd(MGraph G, FloydPath& F)
{
	initFP(G, F);
	for (int mid = 0;mid < G.vexnum;mid++)
		for (int row = 0;row < G.vexnum;row++)
			for (int col = 0;col < G.vexnum;col++)
				if (F.dist[row][mid] + F.dist[mid][col] < F.dist[row][col])
				{
					F.dist[row][col] = F.dist[row][mid] + F.dist[mid][col];
					F.path[row][col] = F.path[row][mid];
				}
}

void printF(FloydPath& F, char x1, char x2)
{
	stack<int> s;
	int v1 = getVertexPos(F.Vertices, x1);
	int v2 = getVertexPos(F.Vertices, x2);
	cout << "Floyd算法" << endl;
	cout << F.Vertices[v1] << "到" << F.Vertices[v2] << "最短路径: ";
	cout << F.Vertices[v1]<<" ";
	int temp = 0, first = v1;
	while (v1 != v2)
	{
		temp = F.path[v1][v2];
		cout << F.Vertices[temp] << " ";
		v1 = temp;
	}
	cout << "权值 " << F.dist[first][v2];
}

完整代码

#include<iostream>__msvc_all_public_headers.hpp
#include<algorithm>__msvc_all_public_headers.hpp
#include<stack>__msvc_all_public_headers.hpp
using namespace std;
const int MaxVertexNum = 100;
const int MaxWeight = 1000;
const int inf = 100000;
typedef char VertexType;
typedef int EdgeType;

struct MGraph									//邻接矩阵
{
	VertexType Vertices[MaxVertexNum];
	EdgeType Edge[MaxVertexNum][MaxVertexNum];
	int vexnum;
	int edgenum;
};

//初始化
void init(MGraph& G)
{
	for (int i = 0;i < MaxVertexNum;i++)
		G.Vertices[i] = 0;
	for (int i = 0;i < MaxVertexNum;i++)
		for (int j = 0;j < MaxVertexNum;j++)
			G.Edge[i][j] = inf;
	G.vexnum = 0;
	G.edgenum = 0;
}

//得到顶点位置
int getVertexPos(VertexType *a, VertexType vertex)
{
	for (int i = 0;i < MaxVertexNum;i++)
		if (a[i] == vertex) return i;
	return false;
}


//插入顶点
bool insertVertex(MGraph& G, VertexType vertex)
{
	if (G.vexnum == MaxVertexNum) return false;	//顶点表已满，返回false
	G.Vertices[G.vexnum++] = vertex;
	return true;
}

//插入边
bool insertEdge(MGraph& G, VertexType vertex1, VertexType vertex2, EdgeType weight)
{
	int v1 = getVertexPos(G.Vertices, vertex1);
	int v2 = getVertexPos(G.Vertices, vertex2);
	if (v1 > -1 && v1<MaxVertexNum && v2>-1 && v2 < MaxVertexNum)
	{
		G.Edge[v1][v2] = G.Edge[v2][v1] = weight;		//无向图
		G.edgenum++;
		return true;
	}
	return false;
}


//最短路径
struct DijkstraPath
{
	VertexType Vertices[MaxVertexNum];//顶点集
	int vexnum;//顶点数
	int visited[MaxVertexNum];//标记
	int	dist[MaxVertexNum];//距离
	int	path[MaxVertexNum];//路径
};
void initSP(DijkstraPath& P)//初始化
{
	for (int i = 0;i < MaxVertexNum;i++)
	{
		P.visited[i] = 0;
		P.dist[i] = 0;
		P.path[i] = 0;
	}
}

int Min(DijkstraPath &P,int n)//P.dist[]最小值的下标
{
	int min = inf;
	int v = 0;
	for (int i = 0;i < n;i++)
		if (!P.visited[i]&& P.dist[i] < min)
		{
			min = P.dist[i];
			v = i;
		}
	return v;
}



void Dijkstra(MGraph G,DijkstraPath &P)
{
	initSP(P);
	int v0 = 0;
	for (int i = 0;i < G.vexnum;i++)//赋值
	{
		P.Vertices[i] = G.Vertices[i];
		P.dist[i] = G.Edge[v0][i];	//顶点到其他顶点的权值
	}
	P.vexnum = G.vexnum;
	P.visited[v0] = 1;
	for (int i = 0;i < P.vexnum;i++)
	{
		int next = Min(P,G.vexnum);//边(Vhead，其他顶点)权值最小的边尾节点next
		P.visited[next] = 1;
		for (int i = 0;i < P.vexnum;i++)
		{
			if ((G.Edge[next][i] + P.dist[next]) < P.dist[i] && !P.visited[i])
			{
				P.dist[i] = G.Edge[next][i] + P.dist[next];
				P.path[i] = next;//记录路径
			}
		}
	}
}

//打印输出

void printP(DijkstraPath P, char x)//从顶点到x的最短路径
{
	stack<int> s;
	int tail=0,in=0;
	P.path[0] =inf;
	tail=in = getVertexPos(P.Vertices, x);//x的顶点序号
	while(in!=inf)//入栈
	{
		s.push(in);
		in = P.path[in];
	}
	cout << "Dijkstra算法"<<endl;
	cout << P.Vertices[0] << "到" << P.Vertices[tail] << "最短路径: ";
	while(!s.empty())//出栈
	{
		int out=s.top() ;
			cout << P.Vertices[out] << " ";
		s.pop();
	}
	cout << "权值：" << P.dist[tail] << endl;
}



struct FloydPath
{
	VertexType Vertices[MaxVertexNum];//顶点集
	int vexnum;//顶点数
	int dist[MaxVertexNum][MaxVertexNum];
	int path[MaxVertexNum][MaxVertexNum];
};

void initFP(MGraph G, FloydPath &F)
{
	for (int row = 0;row < G.vexnum;row++)
		for (int col = 0;col < G.vexnum;col++)
		{
			F.dist[row][col] = G.Edge[row][col];
			F.path[row][col] = col;
		}
	for (int i = 0;i < G.vexnum;i++)//赋值
		F.Vertices[i] = G.Vertices[i];
	F.vexnum = G.vexnum;
}

void Floyd(MGraph G, FloydPath& F)
{
	initFP(G, F);
	for (int mid = 0;mid < G.vexnum;mid++)
		for (int row = 0;row < G.vexnum;row++)
			for (int col = 0;col < G.vexnum;col++)
				if (F.dist[row][mid] + F.dist[mid][col] < F.dist[row][col])
				{
					F.dist[row][col] = F.dist[row][mid] + F.dist[mid][col];
					F.path[row][col] = F.path[row][mid];
				}
}

void printF(FloydPath& F, char x1, char x2)
{
	stack<int> s;
	int v1 = getVertexPos(F.Vertices, x1);
	int v2 = getVertexPos(F.Vertices, x2);
	cout << "Floyd算法" << endl;
	cout << F.Vertices[v1] << "到" << F.Vertices[v2] << "最短路径: ";
	cout << F.Vertices[v1]<<" ";
	int temp = 0, first = v1;
	while (v1 != v2)
	{
		temp = F.path[v1][v2];
		cout << F.Vertices[temp] << " ";
		v1 = temp;
	}
	cout << "权值 " << F.dist[first][v2];
}


void test01()
{
	char A = 'A', B = 'B', C = 'C', D = 'D', E = 'E', F = 'F';
	MGraph g;
	init(g);
	insertVertex(g, A);
	insertVertex(g, B);
	insertVertex(g, C);
	insertVertex(g, D);
	insertVertex(g, E);
	insertVertex(g, F);
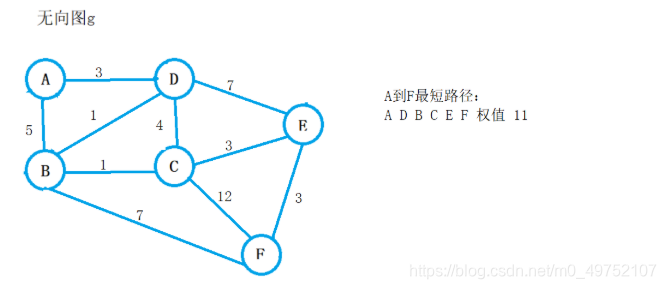
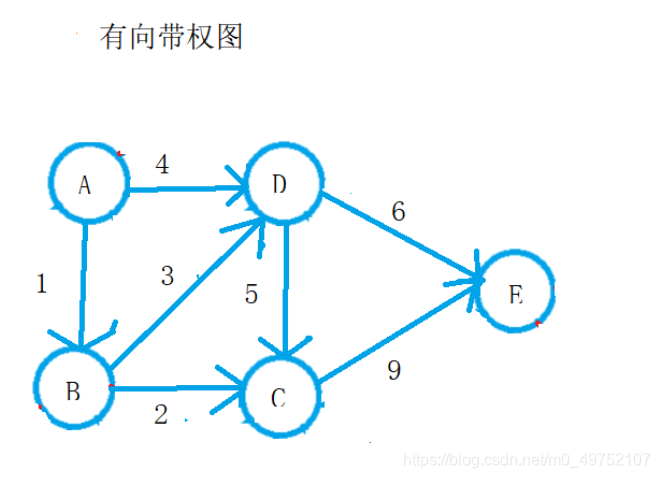
	insertEdge(g, A, B, 5);
	insertEdge(g, A, D, 3);
	insertEdge(g, B, D, 1);
	insertEdge(g, B, C, 1);
	insertEdge(g, C, D, 4);
	insertEdge(g, D, E, 7);
	insertEdge(g, C, E, 3);
	insertEdge(g, B, F, 8);
	insertEdge(g, C, F, 12);
	insertEdge(g, E, F, 3);
	DijkstraPath p;
	Dijkstra(g, p);
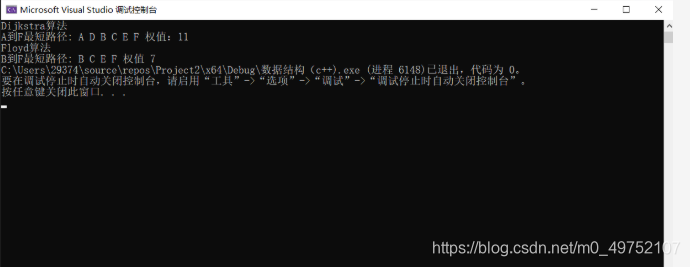
	printP(p, F);//打印从顶点到F的最短路径
	FloydPath f;
	Floyd(g, f);
	printF(f, C, F);//打印最短路径

}




int main()
{
	test01();
	return 0;
}

结果
在这里插入图片描述

拓扑排序

有向无环图，若一个有向图中不存在环，则称为有向无环图，简称DAG图。
AOV网，若用DAG表示一个工程，其顶点表示活动，用有向边<vi,vj>表示活动vi必须先于活动vj进行的这样一种关系，则将这种有向图称为顶点表示活动的网络，记作AOV网。
性质
1.每个顶点出现且只出现一次。
2.若顶点A在序列中排在顶点B的前面，则在图中不存在从顶点B到顶点A的路径。
在这里插入图片描述

代码

//拓扑排序
void ALGraph::TopologicalSort()
{
	stack<int> S;
	for (int i = 0;i < vexnum;i++)
		if (vertices[i].indegree == 0)
			S.push(i);//入度为零的顶点入栈
	int count = 0,t=0;
	VertexType printT[MaxVertexNum];
	while (!S.empty())
	{
		t = S.top();
		printT[count++] = vertices[t].data;//保存输出顶点
		S.pop();
		//list.push(t);//关键路径要用
		for (EdgeNode* p = vertices[t].firstarc;p;p = p->nextarc)//顶点的邻接顶点
		{
			int v = p->adjvex;
			if (!(--vertices[v].indegree))//邻接顶点的入度减一
				S.push(v);//入度为零的顶点入栈

			//if ((vertices[t].ve + p->weight) > vertices[v].ve) {
				//vertices[v].ve = vertices[t].ve + p->weight;
			}
		}
	}
	cout << "拓扑排序：" << endl;//打印输出
	for (int i = 0;i < vexnum;i++)
		cout << printT[i] << " ";
}

关键路径

AOE网，在带权有向图中，以顶点表示事件，以有向边表示活动，以边上的权值表示完成该活动的开销（如完成活动所需要的时间），则称这种有向图为用边表示活动的网络，简称为AOE网。
性质
1.只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才开始。
2.只有在进入某一顶点的各有向边所代表的活动都已结束时，该顶点所代表的事件才能发生。
在这里插入图片描述

代码

#include<iostream>__msvc_all_public_headers.hpp
#include<stack>
using namespace std;

const int MaxVertexNum = 100;

typedef char VertexType;

//边表结点
struct EdgeNode
{
	int adjvex;//邻接点域
	EdgeNode* nextarc;//链域
	int weight;//权值
};

//顶点表结点
typedef struct VexNode
{
	VertexType data;//数据域
	EdgeNode* firstarc;//链域
	int indegree;//入度
	int outdegree;//出度
	int ve;  //记录每个顶点的最早发生时间
	int vl;  //记录每个顶点最迟发生时间
}VexNode,AdjList[MaxVertexNum];//顶点数组

//邻接表
struct ALGraph 
{
	AdjList vertices;//顶点集
	int vexnum;
	int edgenum;
	void TopologicalSort();
	void CriticalPath();
	stack<int> list;
};

//初始化
void init(ALGraph& G)
{
	for (int i = 0;i < MaxVertexNum;i++)
	{
		G.vertices[i].data = 0;
		G.vertices[i].firstarc = 0;
		G.vertices[i].indegree = 0;
		G.vertices[i].outdegree = 0;
		G.vertices[i].ve = 0;
		G.vertices[i].vl = 0;
	}
	G.vexnum = 0;
	G.edgenum = 0;
}

//顶点位置
int getVertexPos(ALGraph& G, VertexType vertex)
{
	for (int i = 0;i < G.vexnum;i++)
		if (G.vertices[i].data ==vertex)
			return i;
	return -1;
}

//插入顶点
bool insertVertex(ALGraph& G, VertexType vertex)
{
	if (G.vexnum == MaxVertexNum) return false;
	G.vertices[G.vexnum++].data = vertex;
	return true;
}

//插入边
void insertEdge(ALGraph& G, VertexType vertex1, VertexType vertex2,int w)
{
	int v1 = getVertexPos(G, vertex1);//得到顶点序号
	int v2 = getVertexPos(G, vertex2);
	EdgeNode* enode = new EdgeNode;
	enode->adjvex =v2;
	enode->nextarc = NULL;
	enode->weight = w;
	if (G.vertices[v1].firstarc == NULL)
	{
		G.vertices[v1].firstarc = enode;//链接下一个顶点
		G.vertices[v1].outdegree++;//出度加一
		G.vertices[v2].indegree++;//入度加一
	}
	else
	{
		EdgeNode* p;
		p = G.vertices[v1].firstarc;
		while (p->nextarc != NULL)
			p = p->nextarc;
		p->nextarc = enode;
		G.vertices[v1].outdegree++;
		G.vertices[v2].indegree++;
	}
	G.edgenum++;
}

//拓扑排序
void ALGraph::TopologicalSort()
{
	stack<int> S;
	for (int i = 0;i < vexnum;i++)
		if (vertices[i].indegree == 0)
			S.push(i);//入度为零的顶点入栈
	int count = 0,t=0;
	//VertexType printT[MaxVertexNum];
	while (!S.empty())
	{
		t = S.top();
		//printT[count++] = vertices[t].data;//保存输出顶点
		S.pop();
		list.push(t);//关键路径要用
		for (EdgeNode* p = vertices[t].firstarc;p;p = p->nextarc)//顶点的邻接顶点
		{
			int v = p->adjvex;
			if (!(--vertices[v].indegree))//邻接顶点的入度减一
				S.push(v);//入度为零的顶点入栈

			if ((vertices[t].ve + p->weight) > vertices[v].ve) {
				vertices[v].ve = vertices[t].ve + p->weight;
			}
		}
	}
	//cout << "拓扑排序：" << endl;//打印输出
	//for (int i = 0;i < vexnum;i++)
	//	cout << printT[i] << " ";
}

void ALGraph::CriticalPath()
{
	TopologicalSort();
	for (int k = 0; k < this->vexnum; k++) {
		vertices[k].vl = vertices[this->vexnum - 1].ve;
	}
	while (!list.empty())
	{
		int t = list.top();
		list.pop();
		for (EdgeNode* p = vertices[t].firstarc;p;p = p->nextarc)//顶点的邻接顶点
		{
			int v = p->adjvex;
			if (vertices[t].vl > (vertices[v].vl - p->weight)) {
				vertices[t].vl = vertices[v].vl - p->weight;
			}
		}
	}
	int ee;
	int el;
	for (int k = 0; k < this->vexnum; k++)
	{
		for (EdgeNode* p = vertices[k].firstarc;p;p = p->nextarc)//顶点的邻接顶点
		{
			int ee;
	int el;
	for (int k = 0; k < this->vexnum; k++)
	{
		for (EdgeNode* p = vertices[k].firstarc;p;p = p->nextarc)//顶点的邻接顶点
		{
			int v = p->adjvex;
			ee = vertices[k].ve;
			el = vertices[v].vl - p->weight;
			if (ee == el)
			{
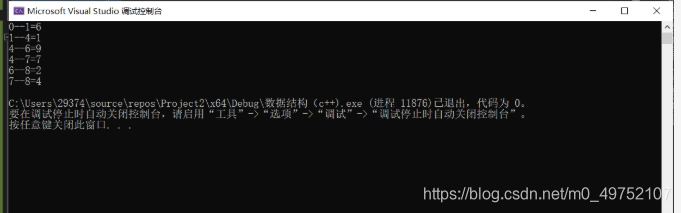
				cout << this->vertices[k].data<< "--"<< this->vertices[v].data<< "="<< p->weight<< endl;
			}
		}
	}
}

void test()
{
	char A = 'v0', B = 'B', C = 'C', D = 'D', E = 'E';
	ALGraph g;
	init(g);
	insertVertex(g, A);
	insertVertex(g, B);
	insertVertex(g, C);
	insertVertex(g, D);
	insertVertex(g, E);
	insertEdge(g, A, B,1);
	insertEdge(g, A, D,4);
	insertEdge(g, B, D,3);
	insertEdge(g, B, C,2);
	insertEdge(g, D, C,5);
	insertEdge(g, D, E,6);
	insertEdge(g, C, E,9);
	g.TopologicalSort();
}

void test01()
{
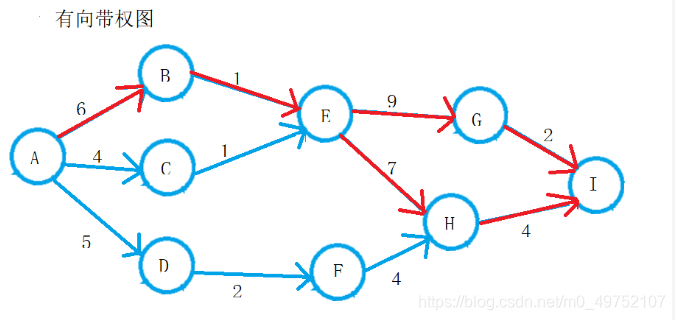
		char A = 'A', B = 'B', C = 'C', D = 'D', E = 'E',F='F',G='G',H='H',I='I';
	ALGraph g;
	init(g);
	insertVertex(g,	A);
	insertVertex(g, B);
	insertVertex(g, C);
	insertVertex(g, D);
	insertVertex(g, E);
	insertVertex(g, F);
	insertVertex(g, G);
	insertVertex(g, H);
	insertVertex(g, I);
	insertEdge(g, A, B, 6);
	insertEdge(g, A, C, 4);
	insertEdge(g, A, D, 5);
	insertEdge(g, B, E, 1);
	insertEdge(g, C, E, 1);
	insertEdge(g, D, F, 2);
	insertEdge(g, E, G, 9);
	insertEdge(g, E, H, 7);
	insertEdge(g, F, H, 4);
	insertEdge(g, G, I, 2);
	insertEdge(g, H, I, 4);
	g.CriticalPath();
}

int main()
{
	//test();
	test01();
	return 0;
}

在这里插入图片描述

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
Java集合深入解析（一）——集合的基本概念
基于微信小程序的毕业设计——在线阅读系统(附源码+论文)
动手学深度学习（pytorch）学习记录29-网络中的网络(NiN)[学习记录]
ISO26262
Maven子项目无法继承父项目的依赖，没有parent标签
类和对象（1）
【笔记】机器翻译学术论文写作方法和技巧（作者：清华大学 刘洋）
计算机网络
VMware Workstation17图文安装（超详细）教程
GIS设计与开发课程设计（一）
;