一、遗传算法
遗传算法
注意:今天和明天,我们将经历大量和大量的进化算法组件的例子(我会给您提供大量的建筑块来试验到以后…)
遗传算法快速概述
• 开发:1970 年代的美国
• 早期名字:J. Holland 和 K. DeJong (1975)
• 通常应用于:
– 离散和持续优化
• 属性特征:
– 不要太快
– 对组合问题的良好启发
• 特殊功能:
– 传统上强调结合好父母的信息(交叉)
– 许多变体,例如繁殖模型、操作符
Holland 的原始遗传算法现在被称为简单遗传算法 (SGA)
• 其他 GA 使用不同的:
– 陈述
– 突变
– 交叉
– 选择机制
SGA 总结
表示 || 二进制字符串
再组合 || N点或均匀
突变 || 具有固定概率的按位翻转
父选择 || 适配比例
幸存者选择 || 所有孩子都代替父母
特性 || 强调交叉
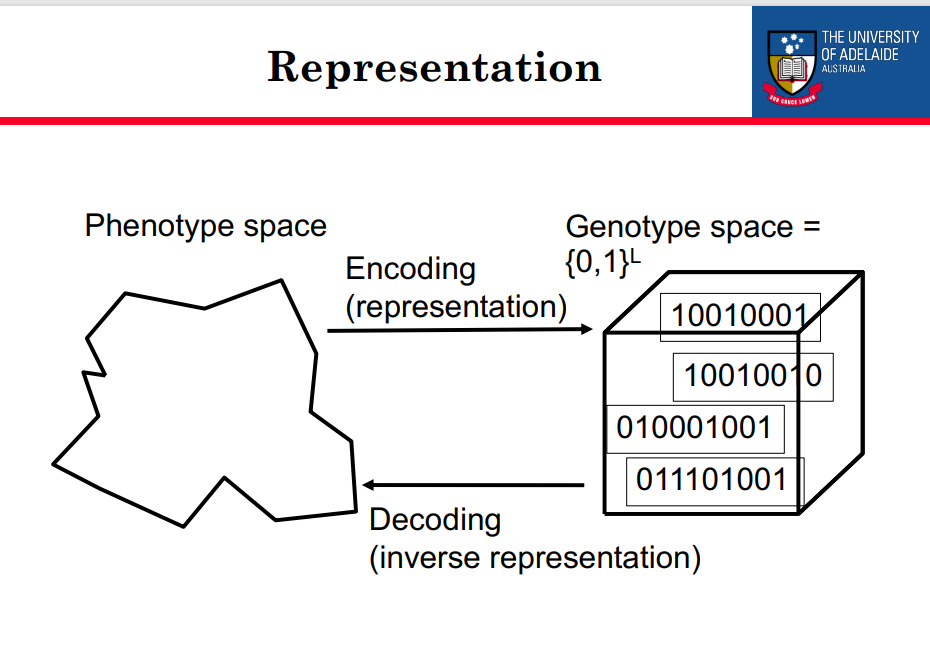
表示
表型空间 <–>基因型空间(编码解码)
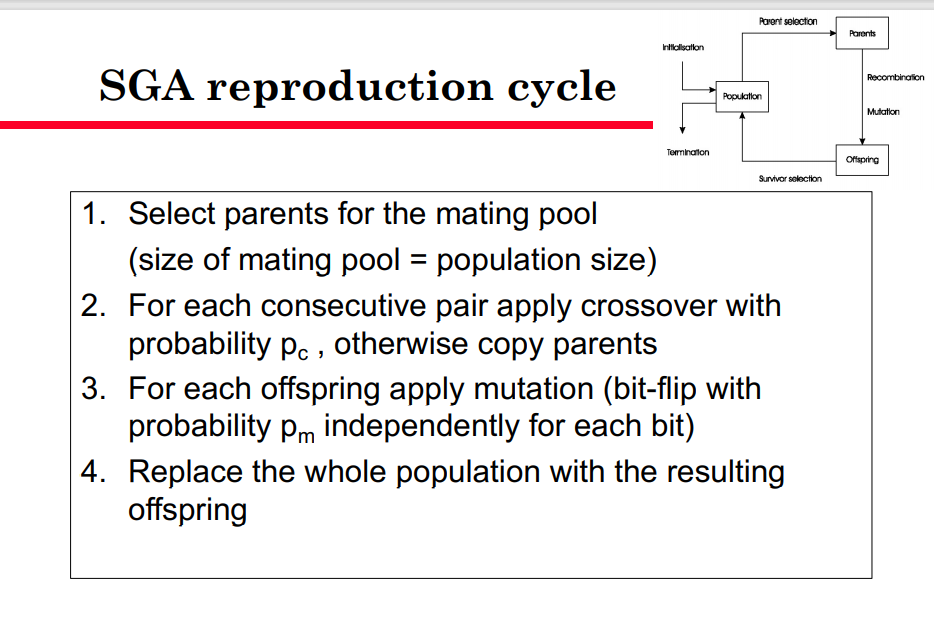
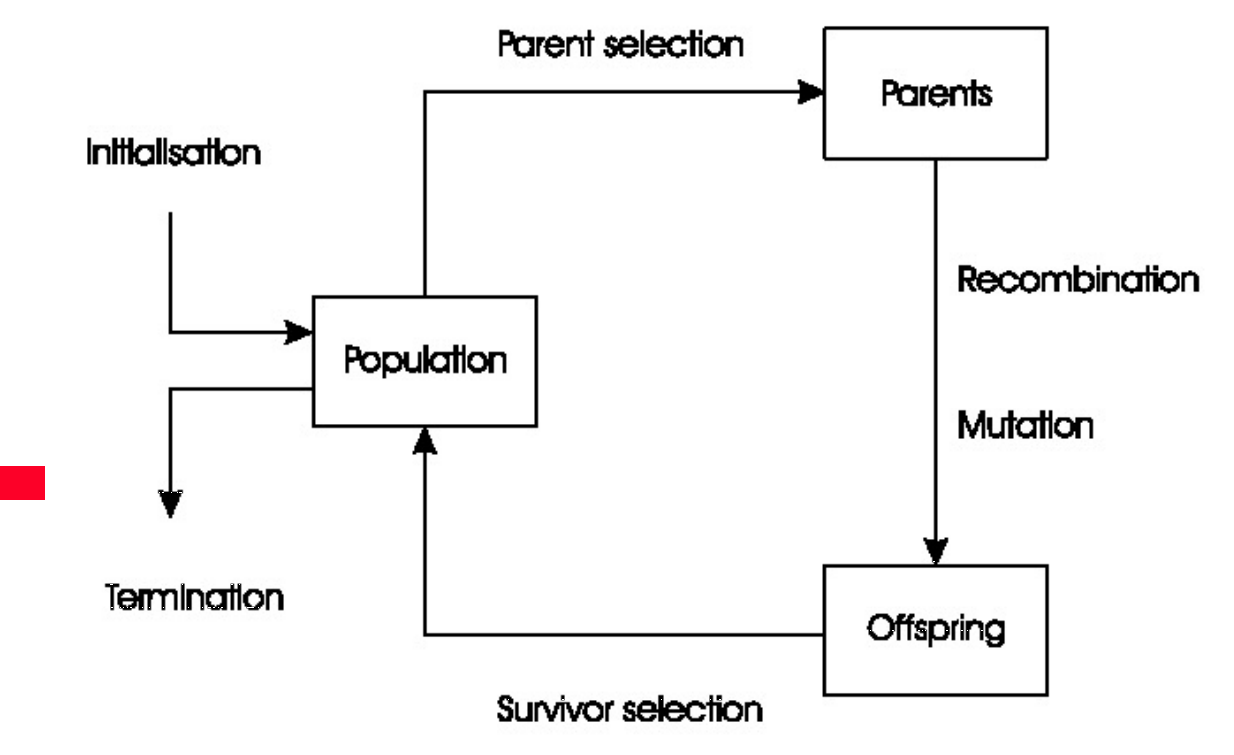
生殖周期
1.为交配池选择亲本(交配池大小=种群大小)
2.对于每个连续的配对应用概率Pc的交叉,否则复制双亲
3.对每个子代应用突变(位翻转,每个位的概率Pm独立)
4.用产生的后代替换整个种群
SGA运算符:选择
主旨:好的人得到更高的机会
–机会与健康成比例
–实施:轮盘赌技术
•为每个人分配一部分轮盘赌
•旋转轮子n次,选择n个人
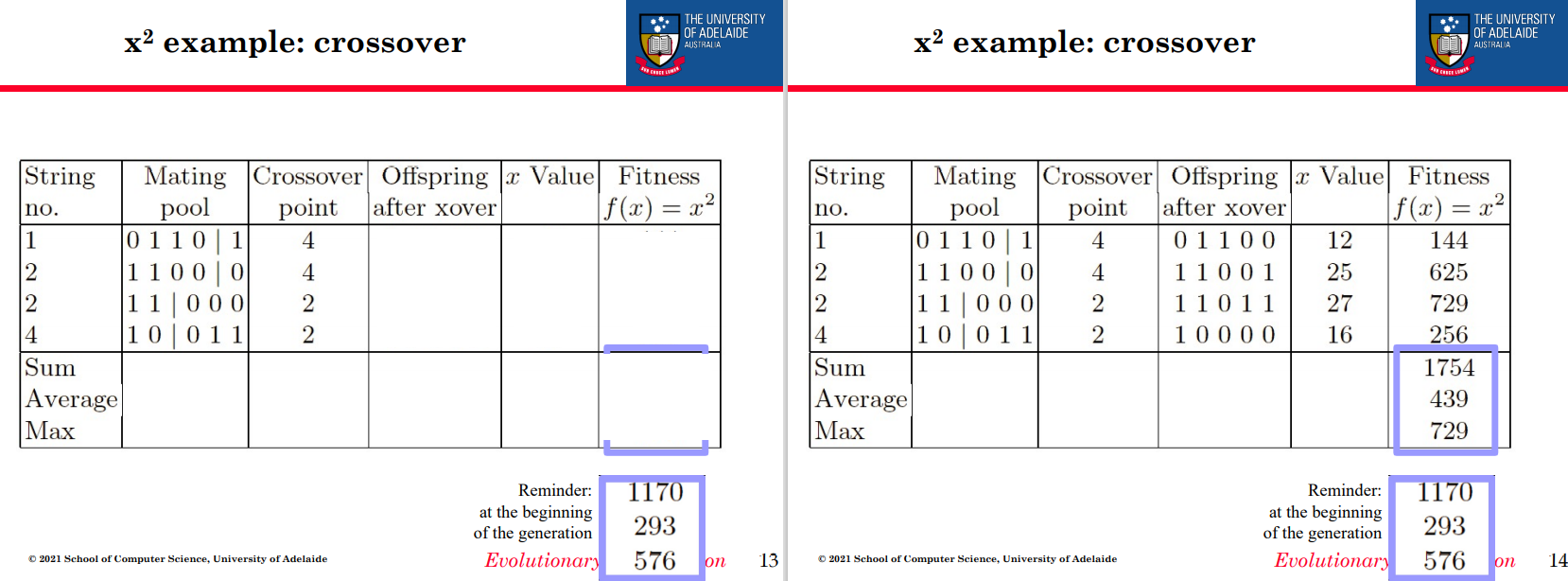
SGA运算符:1点交叉
• 在两个父节点上随机选择一个点
• 在此交叉点拆分父母
• 通过交换尾巴创造孩子
• Pc 通常在 (0.6, 0.9) 范围内
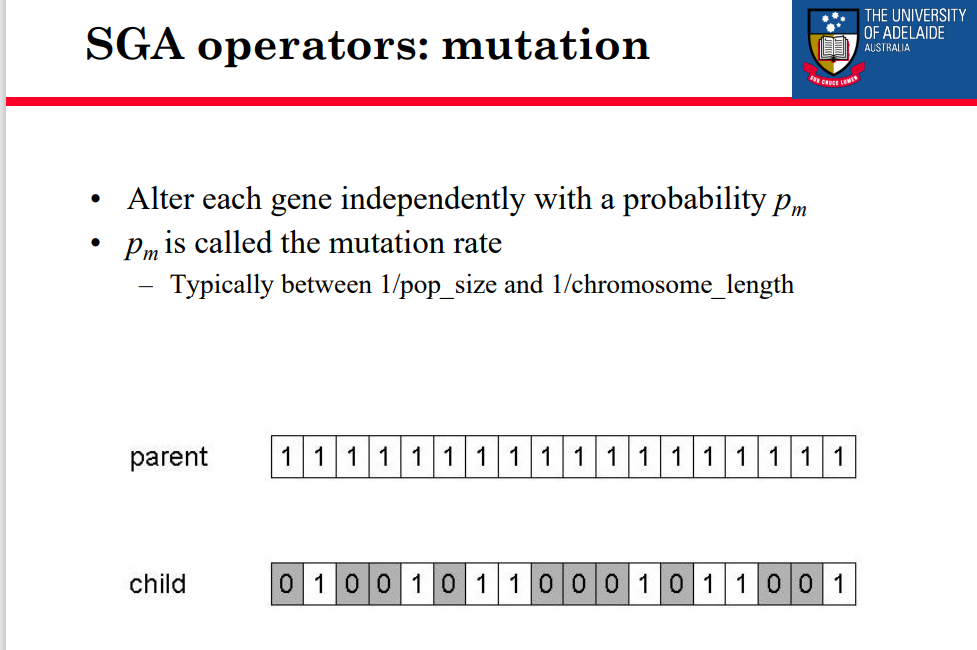
SGA 运算符:变异
•使用PM独立改变每个基因
•PM称为突变率
- 通常在1 / pop_size和1 / chromosome_length之间
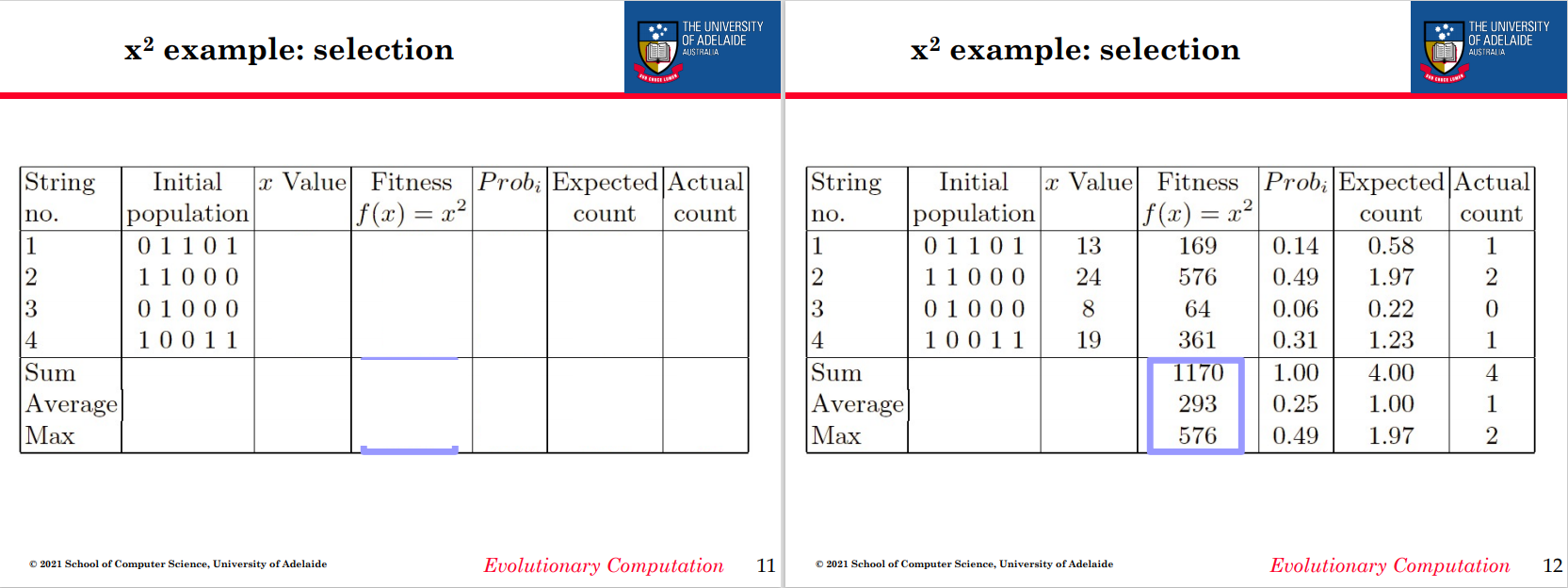
一个例子 [Goldberg '89]
• 简单问题:{0,1,…,31} 上的最大 f(x)=x的平方
• 遗传算法方法:
– 表示:二进制代码,例如 01101 « 13
– 人口规模:4
– 1 点交叉,按位变异
– 轮盘选择
– 随机初始化
• 我们展示了一个手工完成的世代循环
选择
交叉
突变
简单遗传算法
• 是许多(早期)研究的主题
– 很长一段时间内经常用作新型 GA 的基准(现在不再…)
• 显示出许多缺点,例如,
– 代表过于严格
– 变异和交叉仅适用于位串和整数表示
– 可以通过明确的幸存者选择来改进世代人口模型(SGA 代表循环中的第 6 步)
替代交叉算子
单点交叉的性能取决于变量在表示中出现的顺序
–更有可能将彼此接近的基因保持在一起
–无法将来自弦两端的基因结合在一起
–这就是所谓的位置偏差
–如果我们知道问题的结构,就可以利用,但通常情况并非如此
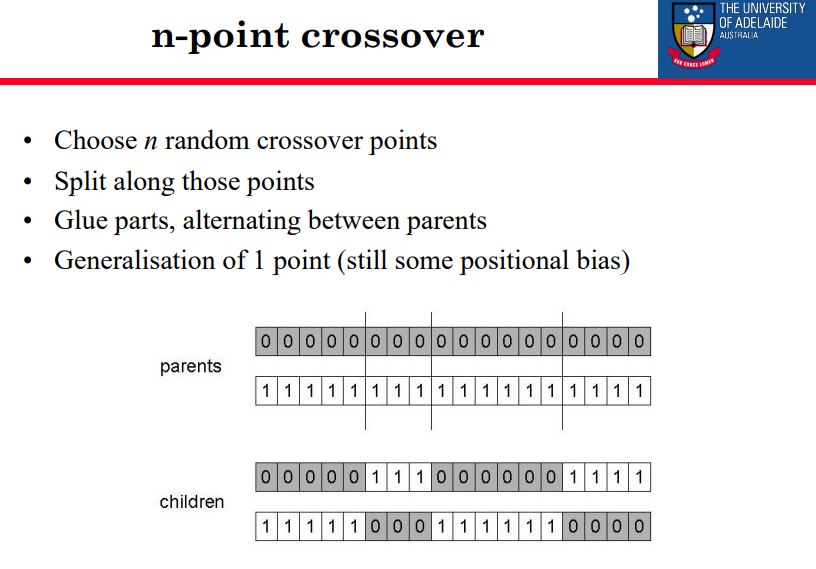
n点交叉
•选择n个随机交叉点
•沿这些点拆分
•粘合部件,在父母之间交替使用
•概括1点(仍然存在一些位置偏差)
均匀交叉
•将“头”分配给父母一方,将“尾”分配给另一方
•为第一个孩子的每个基因掷硬币
•为第二个孩子制作基因的反向拷贝
•继承与地位无关
二、交叉还是变异(讨论)
交叉或变异?
一场长时间的辩论:哪一个更好/必要/主要还是次要。
交叉还是变异?
•长时间的辩论:哪一个更好/必要/主要
•回答(至少,相当广泛的一致意见):
–这取决于问题,但是
–一般来说,两者兼备是好事
–两者都有不同的角色
–仅突变EA是可能的,但仅突变EA一般不起作用
探索:在搜索空间中发现有前景的领域,
即,获取有关问题的信息。
开发:在有前景的领域内进行优化,即使用现有信息。
• 交叉是探索性的,它大跃进到两个(父)区域“中间”的某个区域
• 变异是剥削性的,它会产生随机的小转移,从而保持在父级附近(在其区域内)(注意:在优化的不同阶段,操作符可以产生不同的效果)[注意:并不总是正确的]
•只有交叉才能组合来自双亲的信息
•只有突变才能引入新信息(等位基因)
•交叉不会改变群体的等位基因频率(思维实验:50%的0在群体的第一位,?%在进行n次交叉后)
•为了达到最佳状态,你通常需要一个“幸运”的突变
三、排列表示
•排序/排序问题形成一种特殊类型
•任务是(或可以通过)按一定顺序排列一些对象
–示例:排序算法:重要的是哪些元素出现在其他元素之前(顺序)
–示例:旅行商问题(TSP):重要的是哪些元素相邻出现(相邻)
•这些问题的解决方案通常表示为排列:
–如果有n个变量,则表示为n个整数的列表,每个整数正好出现一次
•问题:
•给定n个城市
•以最短的行程完成完整的旅行
TSP是NP难问题
•编码:
•标记城市1、2、…、n
•一次完整的巡演是一次排列(例如,对于n=4)
[1,2,3,4],[3,4,2,1]正常)
•搜索空间很大:30个城市有30个!» 1032个可能的旅行
突变算子进行排列
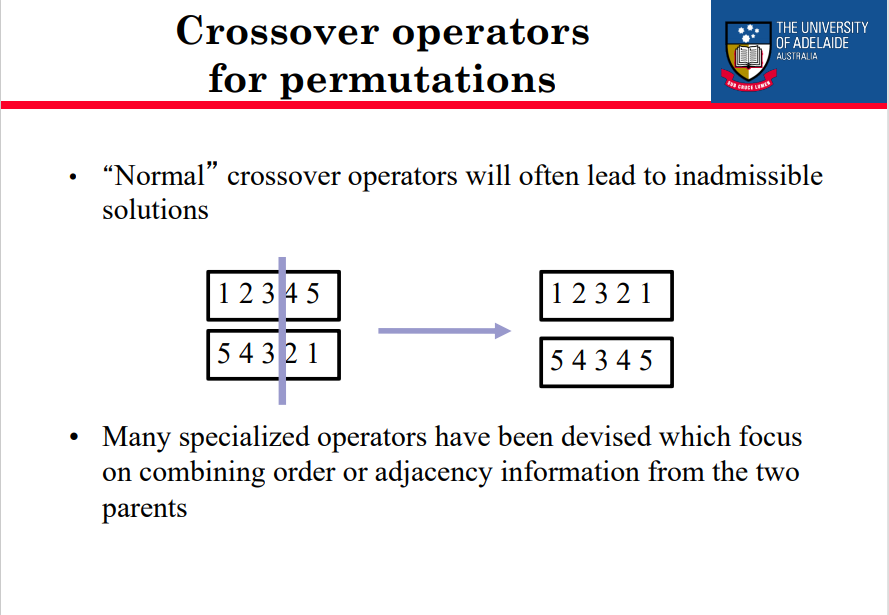
•正常变异算子导致不可接受的解决方案
–例如,位突变:让基因i具有值j
–更改为其他值k意味着k出现两次,j不再出现
•因此必须至少改变两个值
•变异参数现在反映了某些运算符对整个字符串应用一次的概率,而不是在每个位置单独应用
插入序列的突变
•随机选取两个等位基因值
•移动第二个以跟随第一个,移动其余的以适应
•请注意,这样可以保留大部分顺序和相邻信息
交换突变进行排列
•随机挑选两个等位基因并交换位置
•保留大部分邻接信息(4个链接断开),更多地扰乱顺序
置换的倒位突变
•随机挑选两个等位基因,然后反转它们之间的子串。
•保留大多数邻接信息(仅断开两个链接),但破坏订单信息
排列的置乱突变
•随机挑选基因子集
•随机重新排列这些位置的等位基因
(注意:子集不必是连续的)
置换的交叉算子
•“正常”交叉运算符通常会导致不可接受的解决方案
•设计了许多专门的运算符,其重点是组合来自双亲的顺序或邻接信息
顺序交叉(版本1)
其思想是保持元素发生的相对顺序。
非正式程序:
1.从第一个父级中选择任意部分
2.将此部分复制到第一个孩子
3.将不在第一部分的数字复制到第一个孩子:
•从复制零件的切割点开始,
•使用第二个父级的顺序
•末端缠绕
4.与第二个孩子类似,父母角色颠倒
顺序交叉(版本2)
其思想是保持元素发生的相对顺序。
非正式程序:
1.从第一个父对象中选择任意最左边的部分
2.将此部分复制到第一个孩子
3.将不在第一部分的数字复制到第一个孩子:
•从复制零件的切割点开始从左向右,
•使用第二个父级的顺序
•末端缠绕
4.与第二个孩子类似,父母角色颠倒
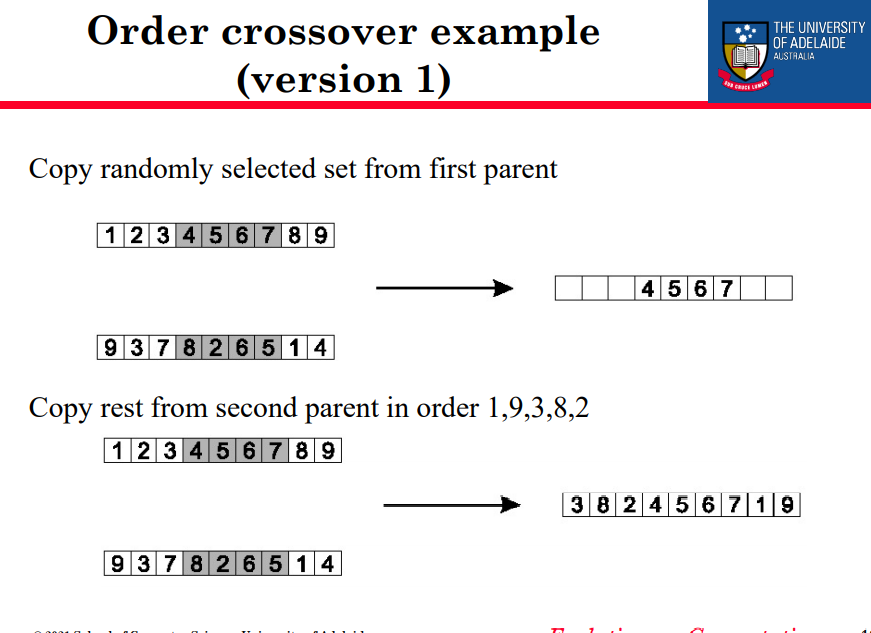
顺序交叉示例(版本1)
从第一个父级复制随机选择的集
按顺序1、9、3、8、2从第二个父级复制其余部分
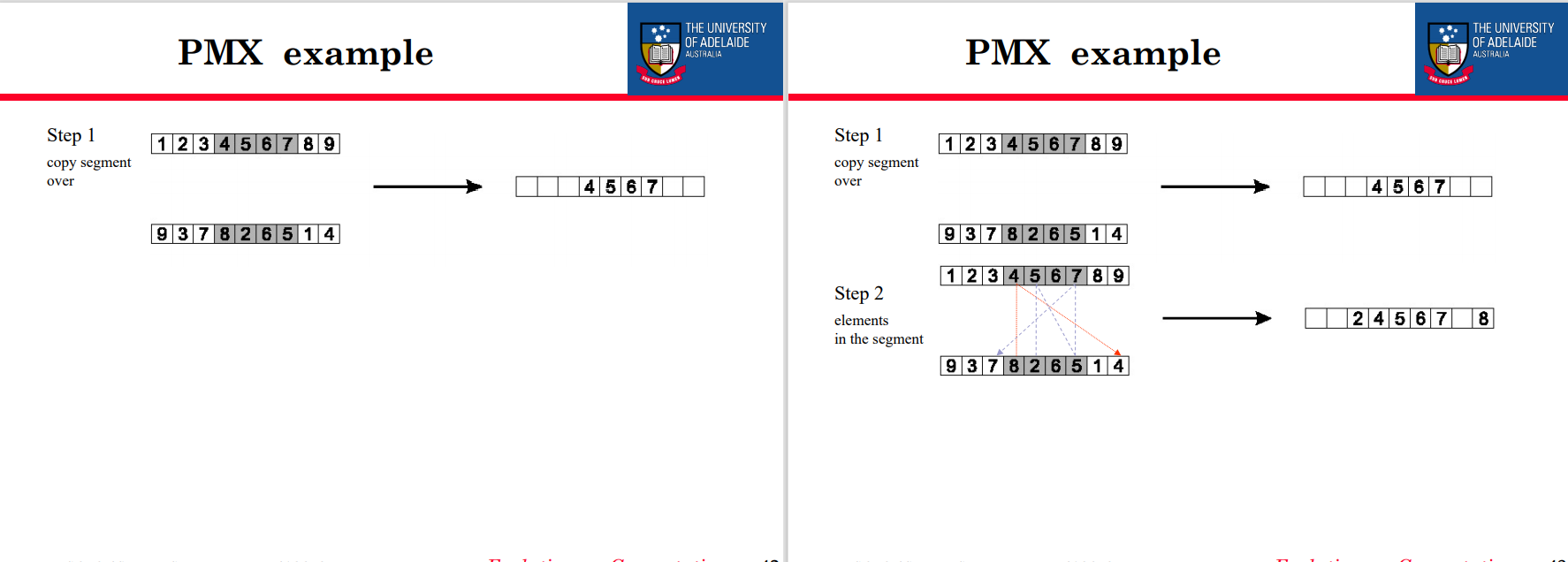
部分映射交叉(PMX)
父母P1和P2的非正式程序:
1.选择随机段并从P1复制
2.从第一个交叉点开始寻找尚未复制的P2段中的元素
3.对于这些中的每一个,我都会在后代看,看看j已从p1中复制了什么
4.将I放入P2中占用的职位,因为我们知道我们不会在其中放置J(如已在后代)
5.如果P2中的J中占用的位置已经填充在后代K中,则将I放入P2中k占用的位置
6.从交叉段处理元素,可以从P2填充后代的其余部分。
第二个孩子是类似地创建的
注意:{5-6}和{7-8}在父母身上,但只有{5-6}在孩子中。
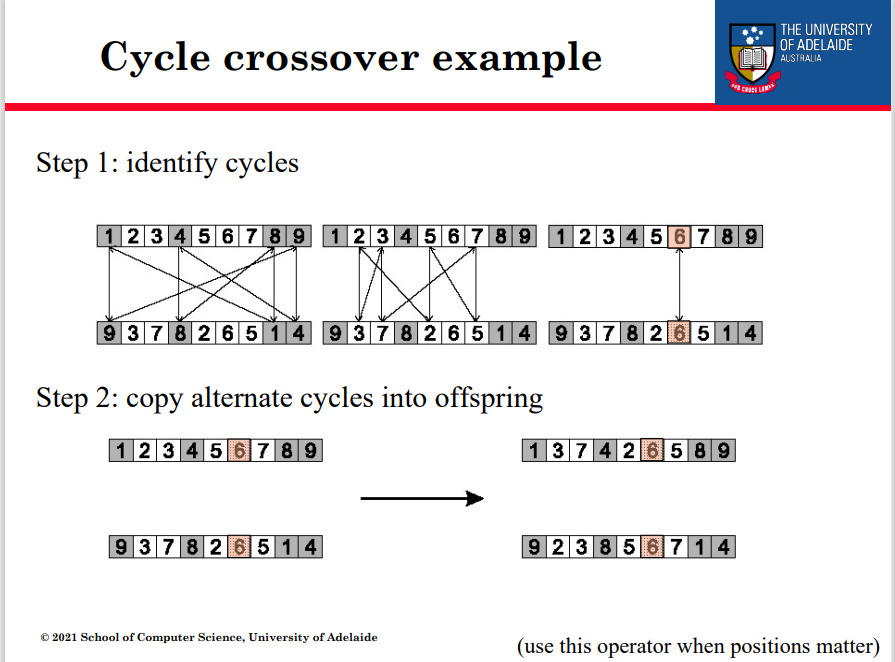
循环交叉
基本想法:
每个等位基因都来自一个父母在一起的位置。
非正式程序:
1.按照以下方式从P1中进行一系列等位基因。
(a)从P1的第一个等位基因开始。
(b)在P2中的相同位置看等位基因。
(c)在P1中使用相同等位基因的位置。
(d)将此等位基因添加到循环中。
(e)重复步骤b至d直到您到达P1的第一个等位基因之前。
2.将第一个孩子的周期等位在第一个父母中的位置上。
3.从第二个父母接下来循环
第1步:识别周期
第2步:将备用周期复制到后代
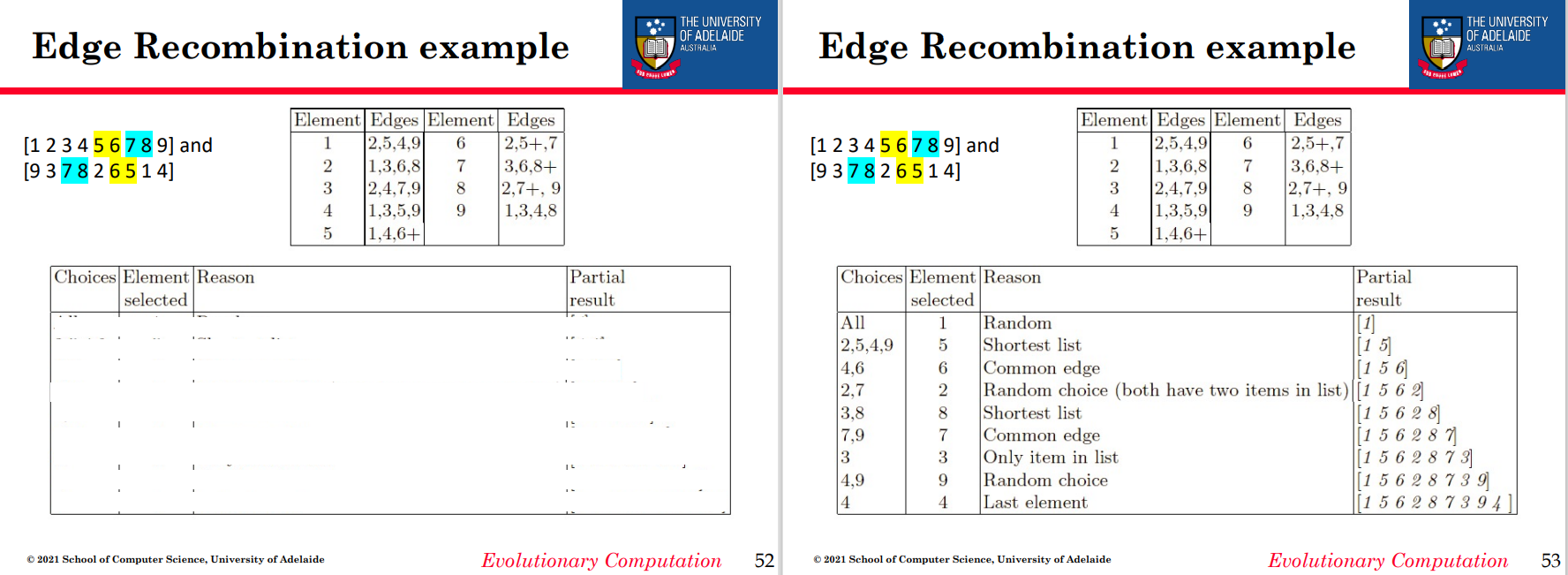
边缘重组
通过构造一个表列表,其中两个父母中存在的边缘,如果边缘普遍,标记为a +
例如 [1 2 3 4 5 6 7 8 9]和[9 3 7 8 2 6 5 1 4]
通过构造一个表列表,其中两个父母中存在的边缘,如果边缘普遍,标记为a +
例如 [1 2 3 4 5 6 7 8 9]和[9 3 7 8 2 6 5 1 4]
边缘重组2
一旦构建边缘表的非正式程序
1.随机选择初始元素并将其放入后代
2.设置变量当前元素=条目
3.从表中删除对当前元素的所有引用
4.检查当前元素列表:
- 如果有一个公共边,则选择它是下一个元素
- 否则选择列表中的条目本身具有最短列表
- 围绕随机分开
5.在到达空名单的情况下: - 检查后代的另一端是为了扩展
- 否则将随机选择新元素
多种重组
•召回我们不会被大自然的实际收缩
•注意到突变使用1个父母,以及“传统”交叉2,延伸到A> 2是自然的检查
•自20世纪60年代以来一直存在,仍然很少,但研究表明了一些有用性
•三种主要类型:
- 基于等位基因频率,例如,P-性投票推广均匀的交叉
- 基于父母的分割和重组,例如对角线交叉推广n点交叉
- 基于实际等位基因上的数值操作,例如,群众交叉中心,普通算术重组算子
人口模型
•SGA使用所谓的世代模型:
- 每个人都刚刚生存一代
- 整个父母被后代所取代
•在比例的另一端是稳态模型(SSGA): - 每代产生一个后代,
- 替代人口的一员,
•生成差距 - 替换人口的比例
-1.0对于SGA,1 / POP_SIZE for SSGA
注意:在EA中有许多事情,许多事情将多于或更少工作。
经验是关键,这就是为什么有编程分配
基于健身的竞赛
•选择可能发生在两个地方:
- 从当前生成选择以参与交配(父选择)
- 从父母+后代选择,进入下一代(幸存者选择)
•选择运营商在整个人身上工作 - 即,他们是独立的
实现示例:SGA
•单个i的预期副本数
E(ni)=µ•f(i)/fñ
(µ=pop.size,f(i)=i的适合度,áfñpop中所有适合度的总和。)
•轮盘赌算法:
–给定一个概率分布,旋转一个单臂轮子n次,做出n个选择
–不保证ni的实际价值
•贝克随机均匀抽样(SUS)算法:
–n均匀分布在轮子上的手臂,旋转一次
–担保下限(E(ni))£ni£ceil(E(ni))
适应度比例选择(FPS)
•问题包括
- 如果剩余的人口较少,一个高度适合的成员可以迅速接管:过早收敛
- 在健身相似时,在运行结束时,丢失选择压力
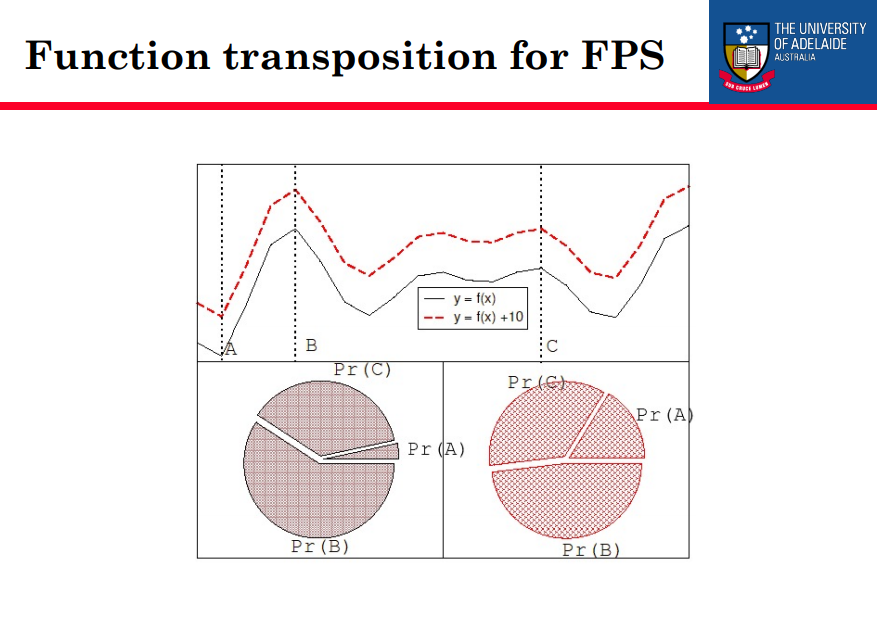
- 高易受功能转换(见下一个幻灯片)
•缩放可以修复最后两个问题 - 窗口:f’(i)= f(i) - b t
•其中B是最糟糕的健身(最后n)代 - Sigma缩放:F’(i)= max(f(i) - (áfÑ-c•sf),0.0)
•其中C是常数(通常2.0),SF是标准偏差,áfÑ是平均的健身
基于等级的选择
•尝试通过基于相对而非绝对适合的选择概率来消除FPS的问题
•根据健身排列人口,然后在最适合排名μ和最差等级的等级上的基础选择概率
•这在算法上强加了排序开销,但与健身评估蒂相比,这通常可以忽略不计
锦标赛选拔
•上述所有方法均依赖全球人口统计
–可能是一个瓶颈,尤其是在并行机器上
–依赖于可能不存在的外部适应功能的存在:例如进化的游戏玩家
•非正式程序:
–随机挑选k个成员,然后从中选出最好的
–重复以上步骤以选择更多个人
•选择i的概率取决于:
–i级
–样本大小k
•k值越高,选择压力越大
–参赛者是否被替换
•挑选而不更换会增加选择压力
–是否最合适的选手总是获胜(确定性的),或者这发生在概率p
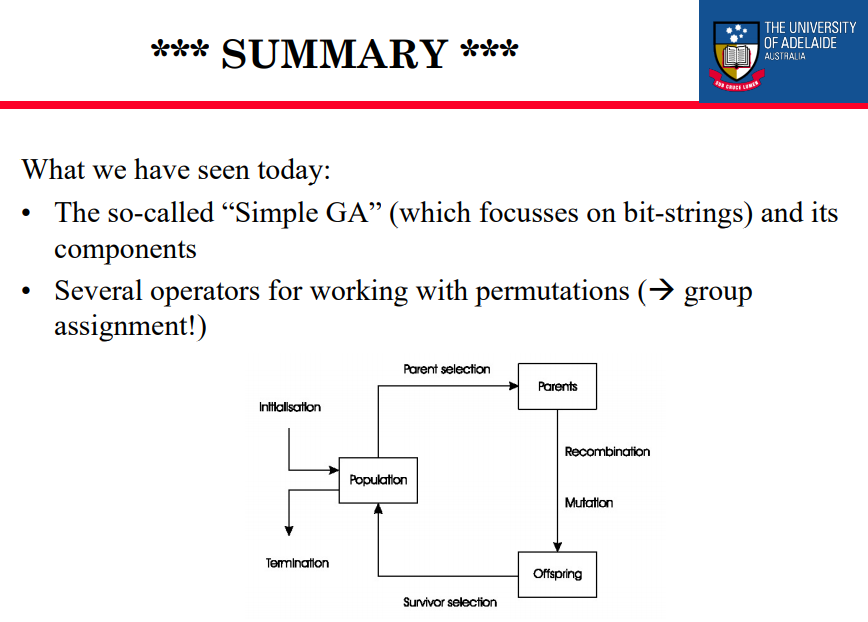
我们今天看到的是:
•所谓的“简单GA”(专注于位串)及其组件
•用于排列的多个运算符(组分配!)