什么是SSM？——状态空间模型（Structured Space Model）

1. 基本定义

• 源于现代控制系统理论。SSM是用于描述序列在各时间步的状态表示，并根据输入预测其下一个状态的模型。原始理论处理连续函数。
  • 输入序列$x(t)$
  • 隐状态表示$h(t)$
  • 预测输出序列$y(t)$

2. 公式表示

-$h^{\prime }(t)=Ah(t)+Bx(t)$
-$y(t)=Ch(t)+Dx(t)$
公式详解文章链接

3. 连续函数离散化——零阶保持

-$h_t=\overline{A}{h}_{t-1}+\overline{B}{x}_t$,$h_0=\overline{B}{x}_0$
-$y_t=\overline{C}{h}_t$
公式详解文章链接

4. 卷积与递归双重属性

公式推导：

$y_2=C{h}_2$
$h_2=\overline{A}{h}_1+\overline{B}{x}_2$
$h_1=\overline{A}{h}_0+\overline{B}{x}_1$
$h_0=\overline{B}{x}_0$

结合起来：

$y_2=C(\overline{A}{h}_1+\overline{B}{x}_2)$
$=C(\overline{A}(\overline{A}{h}_0+\overline{B}{x}_1)+\overline{B}{x}_2)$
$=C(\overline{A}(\overline{A}\overline{B}{x}_0+\overline{B}{x}_1)+\overline{B}{x}_2)$
$=C(\overline{A}\overline{A}\overline{B}{x}_0+\overline{A}\overline{B}{x}_1+\overline{B}{x}_2)$
$=C{\overline{A}}^2\overline{B}{x}_0+C\overline{A}\overline{B}{x}_1+C\overline{B}{x}_2$

卷积运算解释：

我们可以将输出$y_k$看作卷积运算：
$y_k=(C{\overline{A}}^k\overline{B}C{\overline{A}}^{k-1}\overline{B}...C\overline{A}\overline{B}C\overline{B})\left(\begin{array}{c}{x}_0\\ x_1\\ ...\\ x_k\end{array}\right)$
视为卷积核$K=(C{\overline{A}}^k\overline{B}C{\overline{A}}^{k-1}\overline{B}...C\overline{A}\overline{B}C\overline{B})$，只要确定了$A,B,C$，就可以进行并行计算。

递归运算解释：

同样地，输出$y_k$也可以看作递归运算：
$y_k=C\overline{A}{h}_{k-1}+\overline{B}{x}_k$

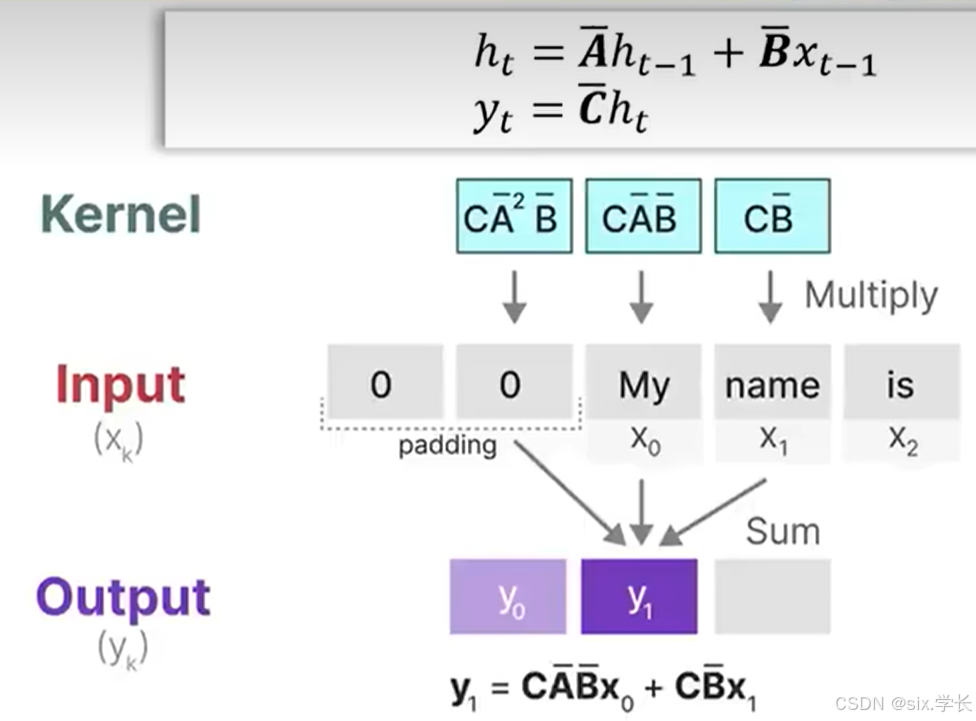
这个图展示了状态空间模型（SSM）中的卷积与递归运算，特别是如何将输入序列$x_k$转换为输出序列$y_k$的过程。让我们详细解释公式和图示内容。

图示内容和公式

公式：

$h_t=\overline{A}{h}_{t-1}+\overline{B}{x}_{t-1}$
$y_t=\overline{C}{h}_t$

这些公式描述了状态更新和输出生成的过程。

图示分解：

1. Kernel（卷积核）：
   -$\overline{C}{\overline{A}}^2\overline{B}$
   -$\overline{C}\overline{A}\overline{B}$
   -$\overline{C}\overline{B}$

2. Input（输入序列$x_k$）：

   • 序列输入$x_0,x_1,x_2$表示为 “My name is” 。
   • 序列开头使用零填充（padding），表示开始状态的初始化。

3. Output（输出序列$y_k$）：
   -$y_0$,$y_1$,$y_2$分别表示不同时间步的输出。

核心步骤：

1. 初始填充和输入：

• 在时间步$t=0$时，输入$x_0$前有一个零填充，表示初始状态。
• 输入序列表示为 [0, “My”, “name”, “is”]。

2. 卷积运算：

• 卷积核分别为$\overline{C}{\overline{A}}^2\overline{B}$、$\overline{C}\overline{A}\overline{B}$、$\overline{C}\overline{B}$。
• 卷积核与输入序列进行乘法运算。

3. 求和生成输出：

• 在每个时间步，进行加法求和，生成输出序列。

详细过程：

-$y_0=\overline{C}\overline{B}{x}_0$，此时$x_0$= “My”。
-$y_1=\overline{C}\overline{A}\overline{B}{x}_0+\overline{C}\overline{B}{x}_1$，此时$x_0$= “My”，$x_1$= “name”。
-$y_2=\overline{C}{\overline{A}}^2\overline{B}{x}_0+\overline{C}\overline{A}\overline{B}{x}_1+\overline{C}\overline{B}{x}_2$，此时$x_0$= “My”，$x_1$= “name”，$x_2$= “is”。

示例计算：

• 假设$\overline{A},\overline{B},\overline{C}$为特定的数值矩阵，通过上述步骤进行计算得到各个时间步的输出$y_k$。

通过这种卷积与递归相结合的方式，状态空间模型可以有效地处理时间序列数据，捕捉其动态特性，实现输入到输出的高效转换。