Accuracy & Precision & Recall & F1
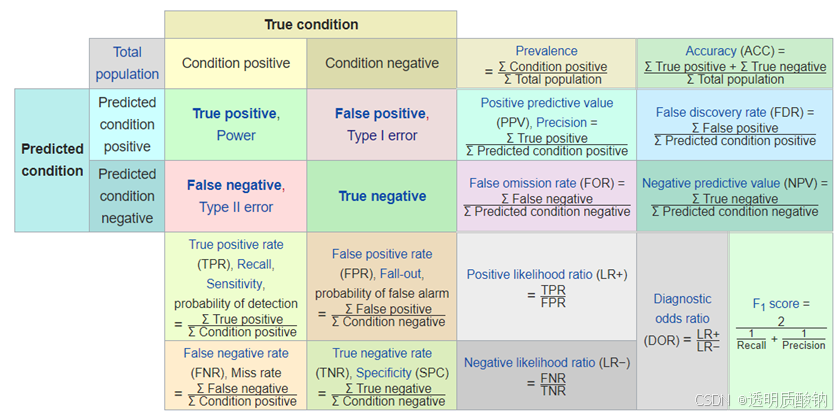
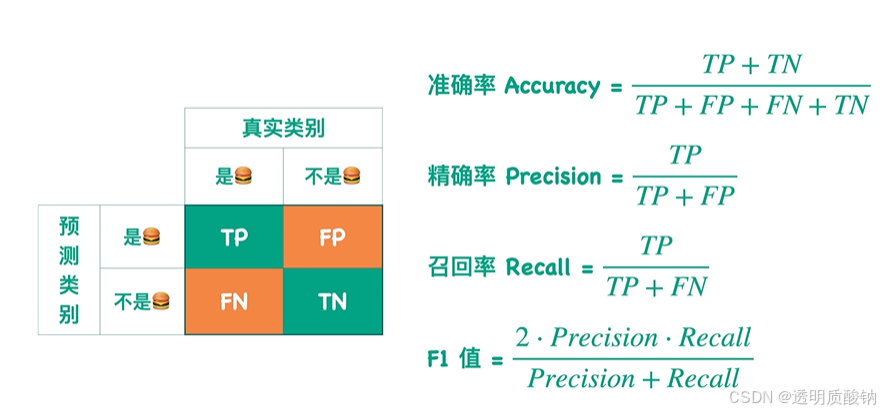
准确率 Accuracy
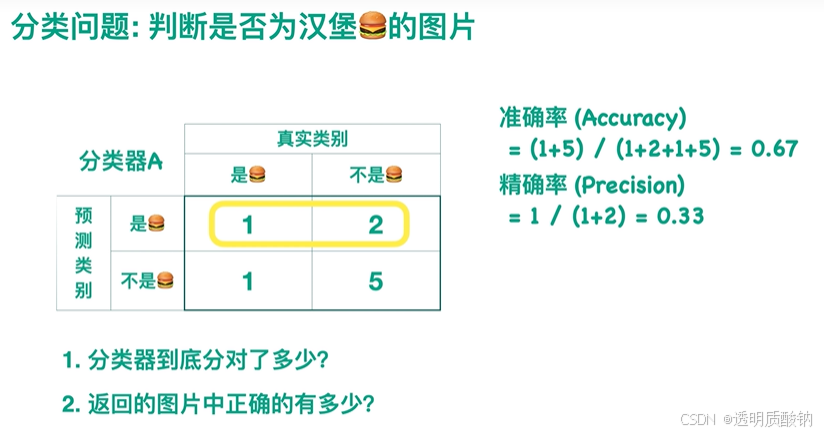
A c c u r a c y = T T + T F A L L Accuracy = \frac{TT + TF}{ALL} Accuracy=ALLTT+TF
1.分类器到底分对了多少?
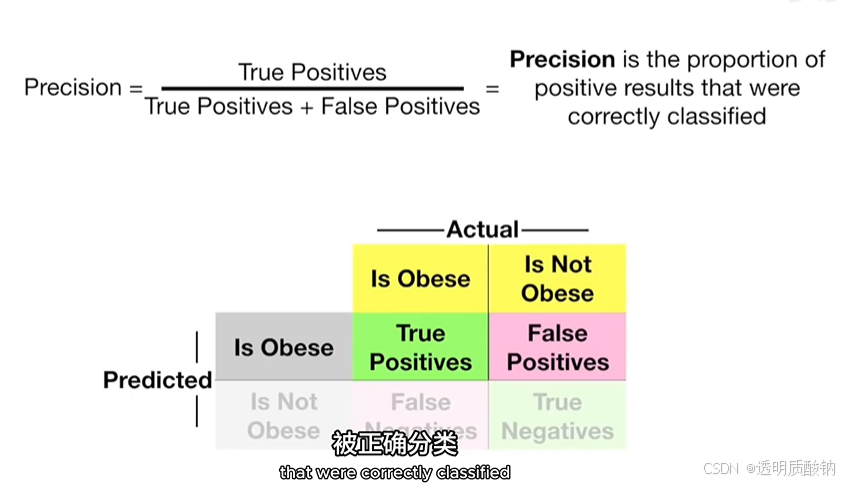
精确率 Precision
2.返回的图片中正确的有多少?
召回率 / 查全率 Recall
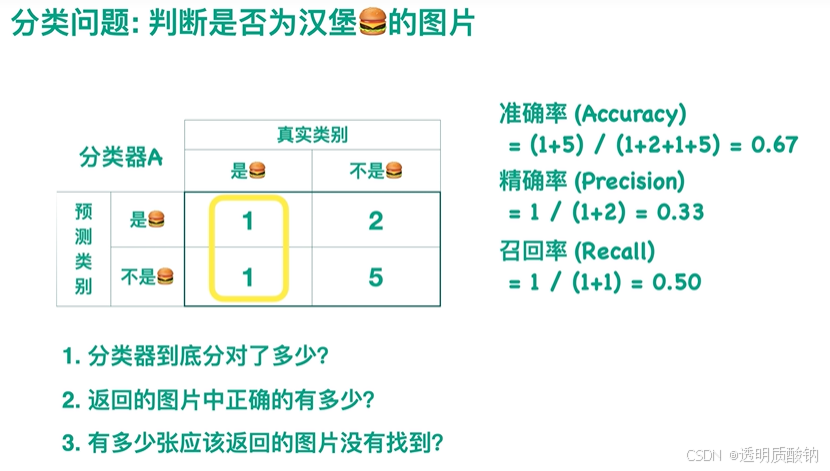
3.有多少张应该返回的图片没有找到?
这个问题可以通过Recall值来体现(因为Recall值 = 1 - 有多少张应该返回的图片没有找到 / 应该返回的图片总数,该公式中除了"有多少张应该返回的图片没有找到"的值是变量以外,其它均为常数)
召回率代表“本应返回的照片中,实际返回了多少”
Recall为返回的图片中汉堡的图片的数目 / 测试集样本中所有汉堡的图片的数目。
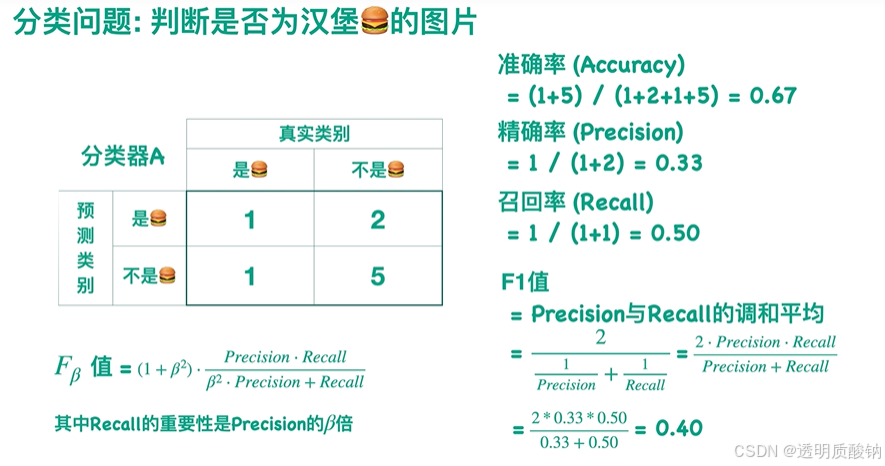
F1值
由上图可以看出(召回率100%的情况下精确率非常低):不能一味地要求召回率高,也不能一味地要求精确率高。否则会导致另一个值相对较低。因此此时我们就提出了一个新的值——F1值
总结
二分类:
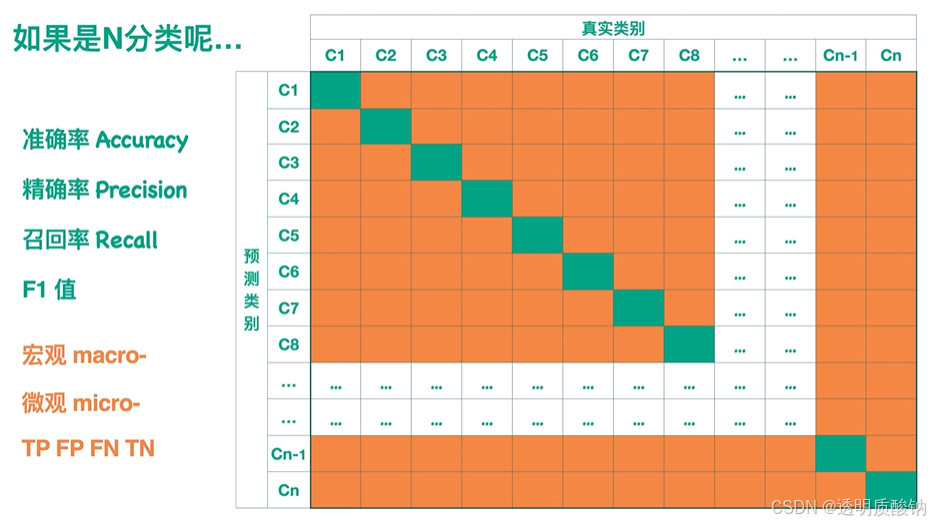
多分类
- 准确率 A c c u r a c y = 所有的绿色求和 A L L Accuracy = \frac{所有的绿色求和}{ALL} Accuracy=ALL所有的绿色求和
- 精确率往往单独看每一类,比如C6, P r e c i s i o n = C 6 的这个绿色 C 6 整一行样本总数 Precision = \frac{C6的这个绿色}{C6整一行样本总数} Precision=C6整一行样本总数C6的这个绿色
- 召回率同上, R e c a l l = C 6 的这个绿色 C 6 整一列样本总数 Recall = \frac{C6的这个绿色}{C6整一列样本总数} Recall=C6整一列样本总数C6的这个绿色
- F1值是精确率和召回率的调和平均
如上,可以求出每一类的Precision、Recall、F1
如果想知道整体的Precision、Recall、F1,可以直接求平均或者求加权平均
实际上刚才求的是宏观macro的Precision、Recall、F1,相应地,我们也可以求微观micro的Precision、Recall、F1:
针对每一类,都有TP、FP、TN、FN。若要求整个模型的TP,可以把每一类的TP都加起来。这样就得到了针对整个模型的TP、FP、TN、FN。再套入公式,就可以得到微观micro的Precision、Recall、F1
注意如果模型针对一个输入只返回一个label,也就是说一个输入只能对应一个类别的话,这样求出的微观micro的Precision、Recall、F1都会是相等的,且都等于Accuracy
ROC曲线 & AUC值
这个视频里举的例子基于 逻辑回归,但RPC & AUC应用范围不止如此
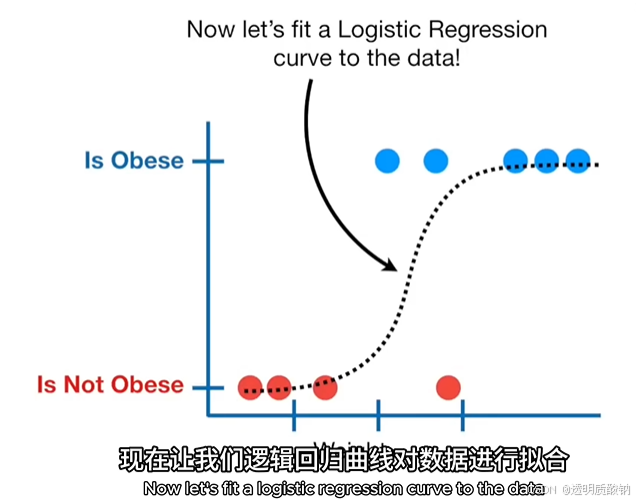
y轴表示老鼠是否肥胖,x轴表示老鼠的体重
使用逻辑回归曲线对数据进行拟合的结果如上图
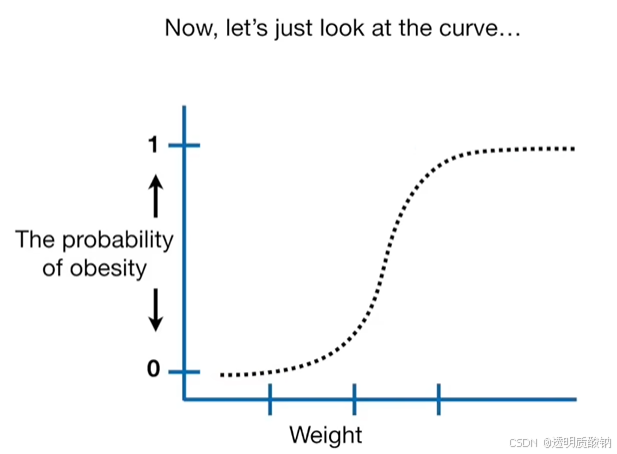
当我们进行逻辑回归时,y轴被转换为老鼠肥胖的概率。如下图:
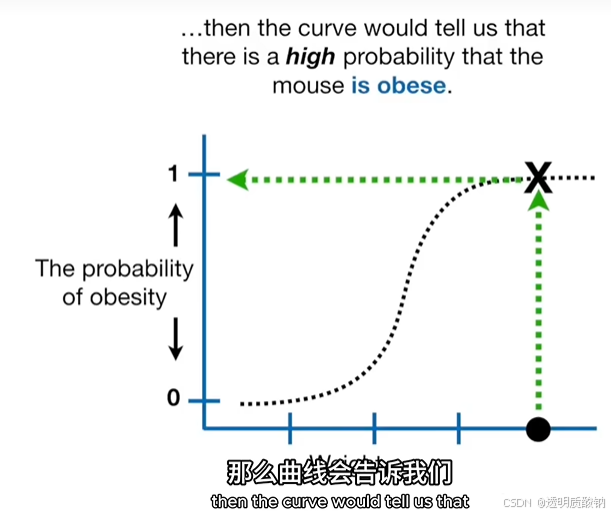
如果现在有一只很重的老鼠,那么曲线会告诉我们这只老鼠肥胖的概率很高,如下图:
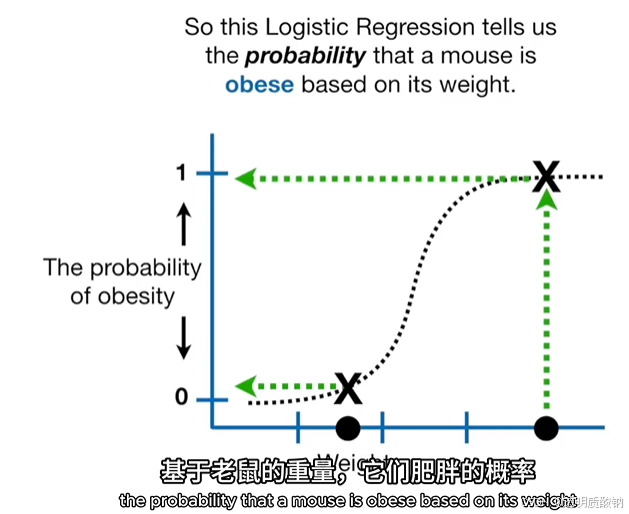
所以这个逻辑回归告诉我们:基于老鼠的重量,它们肥胖的概率。如下图
然而,如果我们想把老鼠归类为肥胖或者不肥胖,那么我们需要一种方法将概率转化为分类
对小鼠进行分类的一种方法是将阈值设置为0.5,把所有肥胖概率大于0.5的老鼠归类为肥胖,并将所有肥胖概率小于等于0.5的老鼠归类为非肥胖
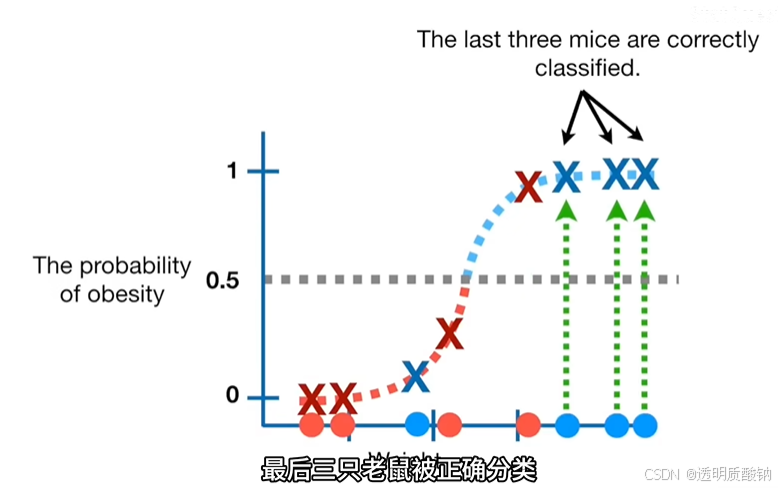
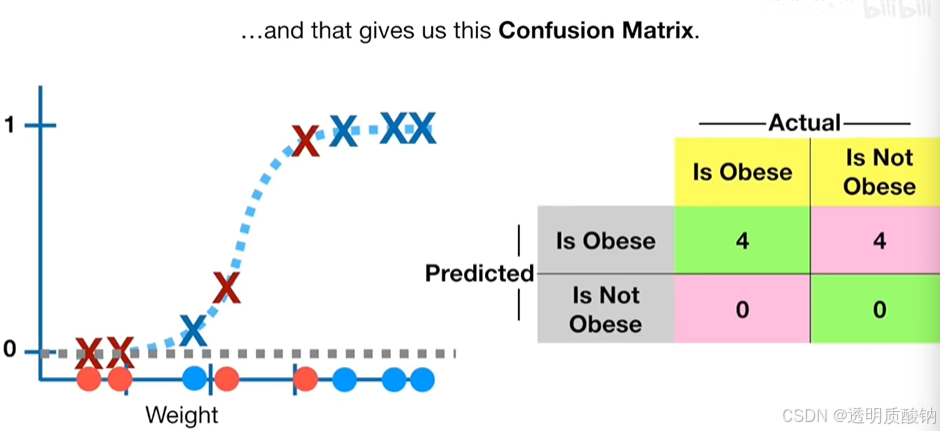
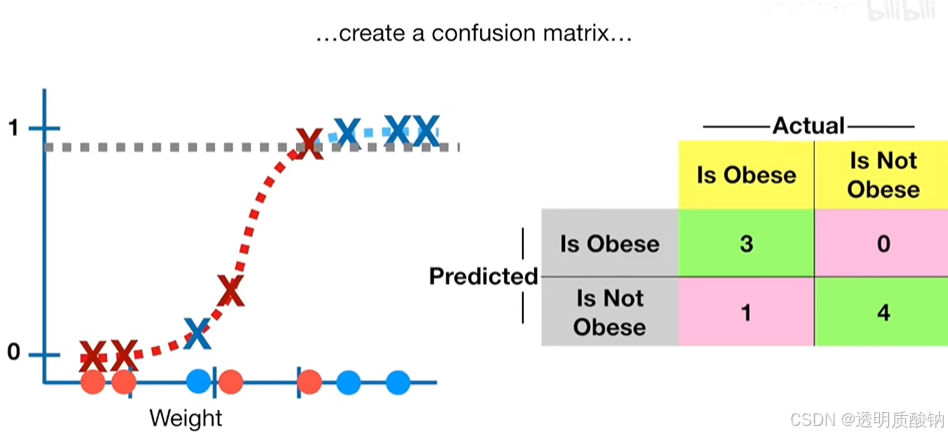
为了来评估这个分类阈值为0.5的逻辑回归模型的效果,我们可以用已知肥胖或非肥胖的老鼠做测试:如下图:
这是四只已知非肥胖的新老鼠的重量,以及这是四只已知肥胖的新老鼠的重量
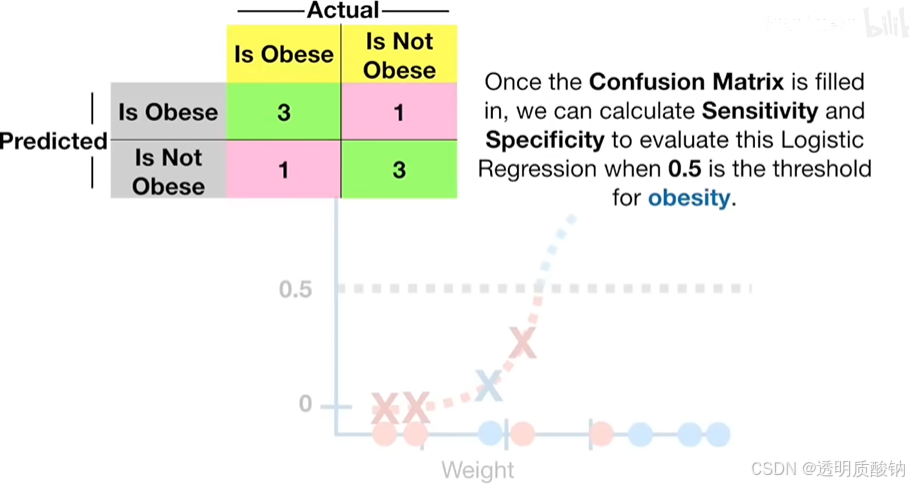
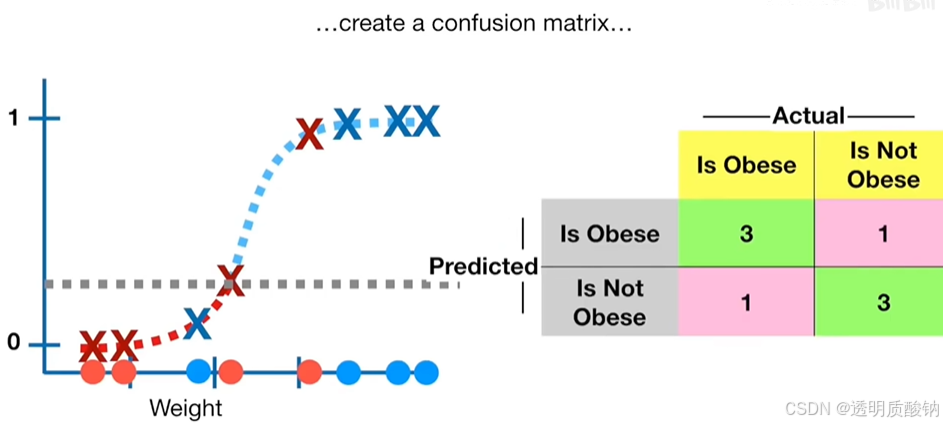
现在我们创建一个混淆矩阵confusion matrix来总结分类的结果,如下图
如下图,完成了混淆矩阵之后,我们可以计算敏感性和特异性,来评估这个肥胖阈值为0.5的逻辑回归模型
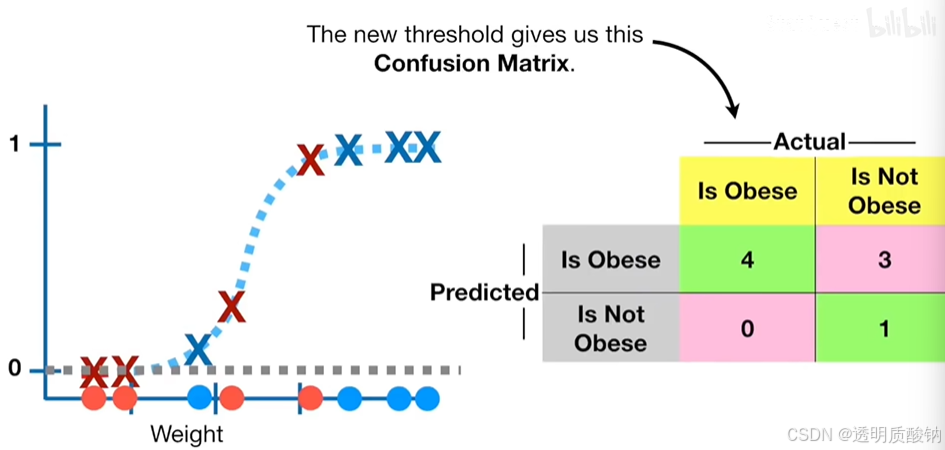
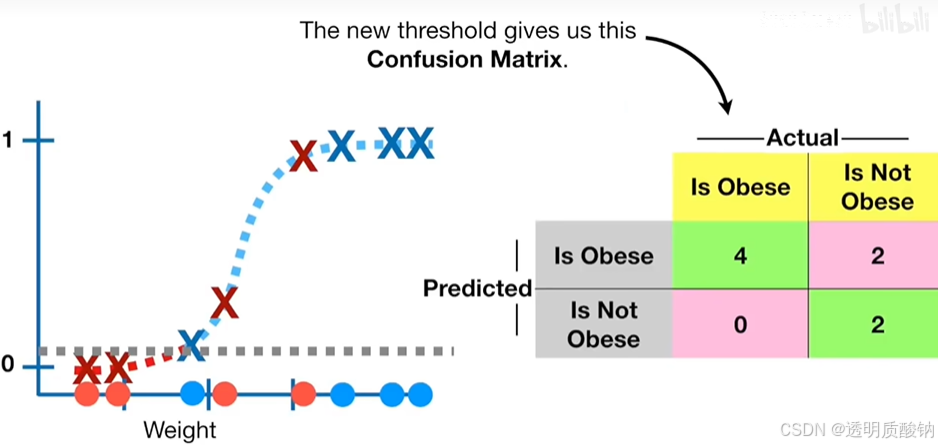
现在,当我们使用不同的阈值来决定样本是否肥胖时会发生什么?
比方说,正确分类每个真正肥胖的样本非常重要,我们可以将阈值设置为0.1:
这将导致四只肥胖老鼠都被正确分类,但是这也会增加假阳性的数量。较低的阈值,也会减少假阴性的数量
注意如果使用不是0.5的阈值的想法让你大吃一惊:想象一下现在我们不再将样本分类为肥胖或不肥胖,而是将其归类为感染了埃博拉病毒或没有感染埃博拉病毒。在这种情况下,正确分类每个感染埃博拉病毒的样本是绝对重要的。这样才能将病毒爆发风险降至最低,即使这会导致更多的假阳性
阈值可以设置为0到1之间的任何值,我们如何确定哪个阈值是最好的呢?
首先,我们不需要测试每一个选项:例如,这些阈值会产生完全相同的混淆矩阵
但即使我们对每个重要的阈值都计算一个混淆矩阵,这也将导致令人头疼的大量混淆矩阵
所以与其被混淆矩阵弄得不知所措,
Receiver Operator Characteristic Curve
接收者操作特性receiver operator characteristic(ROC)图graphs 提供了一种简单的方法来总结所有信息
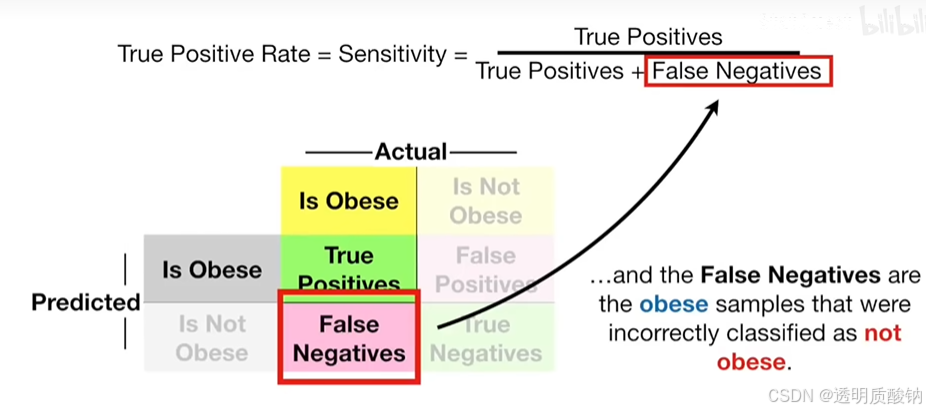
y轴显示真阳性率,也就是敏感性。真阳性率 = 真阳性 / (真阳性 + 假阴性)
因此y轴告诉你被正确归类为肥胖的样本比例
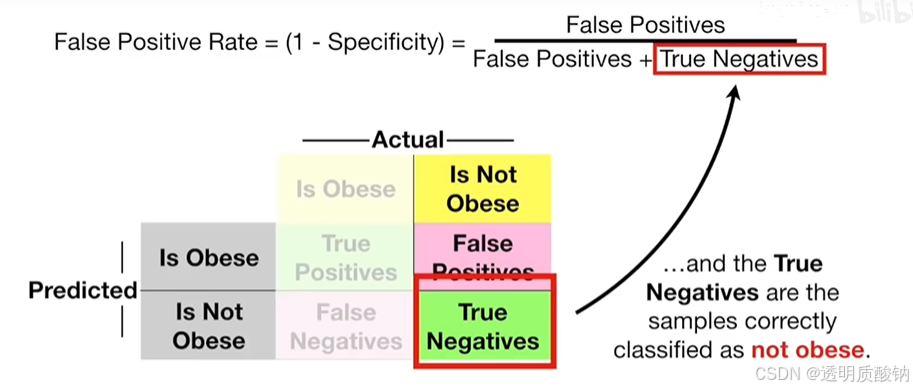
x轴表示假阳性率,等于1-特异性,
假阳性率 = 假阳性 / (假阳性 + 真阴性)
因此x轴告诉你多大比例的非肥胖样本被错误地分类
为了更好地了解ROC是如何运作的:
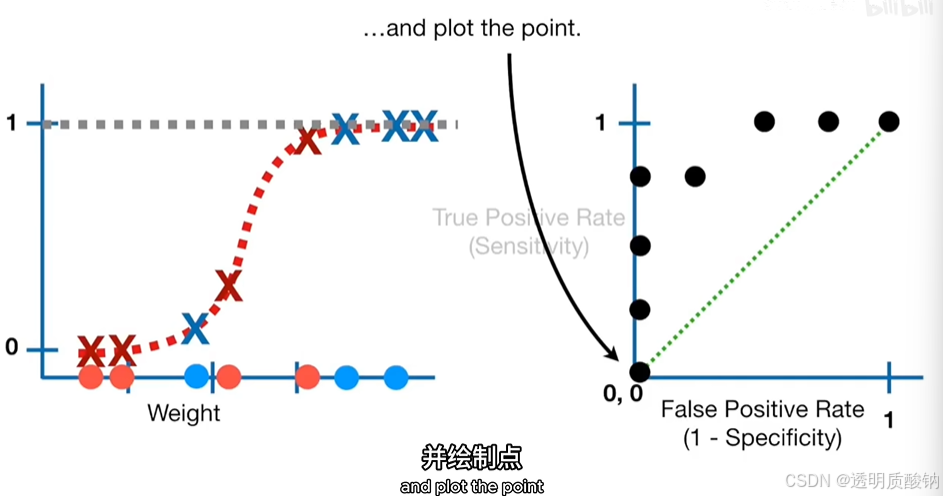
我们将从使用将所有样本归类为肥胖的阈值开始,首先得到如下这个混淆矩阵
现在来提高阈值,使得除了最轻的样本之外,所有的样本都被归为肥胖,得到如下的混淆矩阵
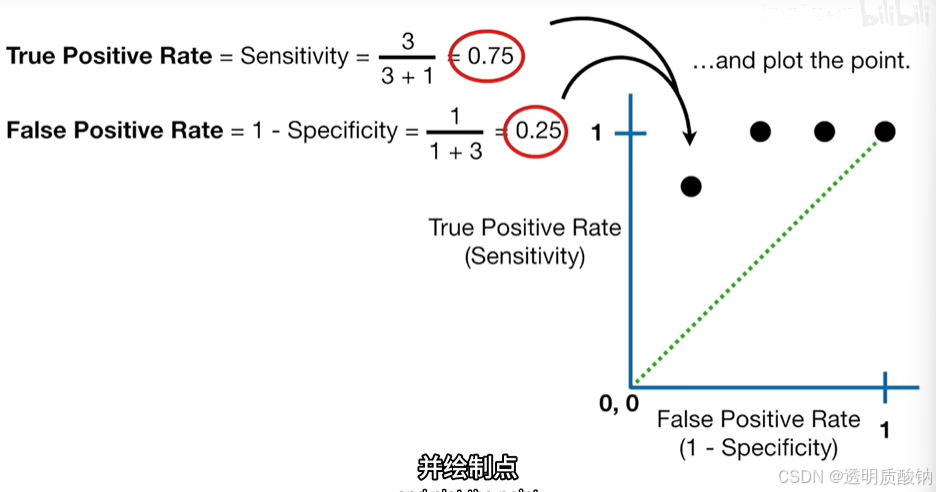
继续提高阈值,所以除了俩个最轻的样本之外,所有样本都被称为肥胖
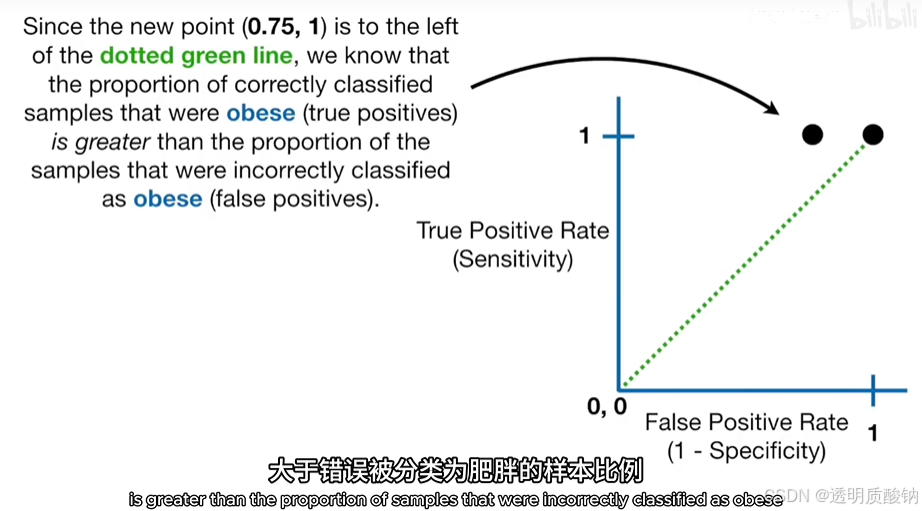
如上图,新的点在绿色虚线的左边还要远的地方,这表明新的阈值进一步减少了被错误归类为肥胖的样本比例,也就是说新的阈值是目前为止最好的一个
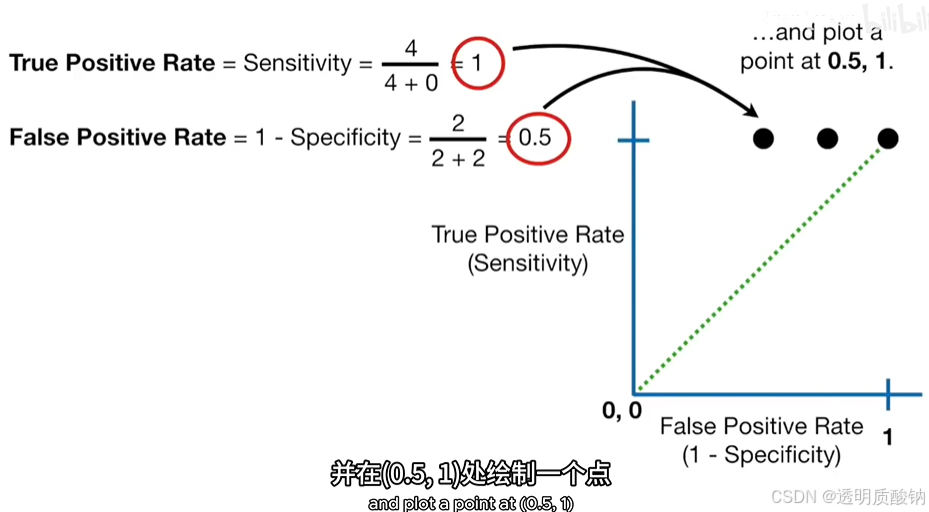
继续提高阈值,
并绘制其点,如下图
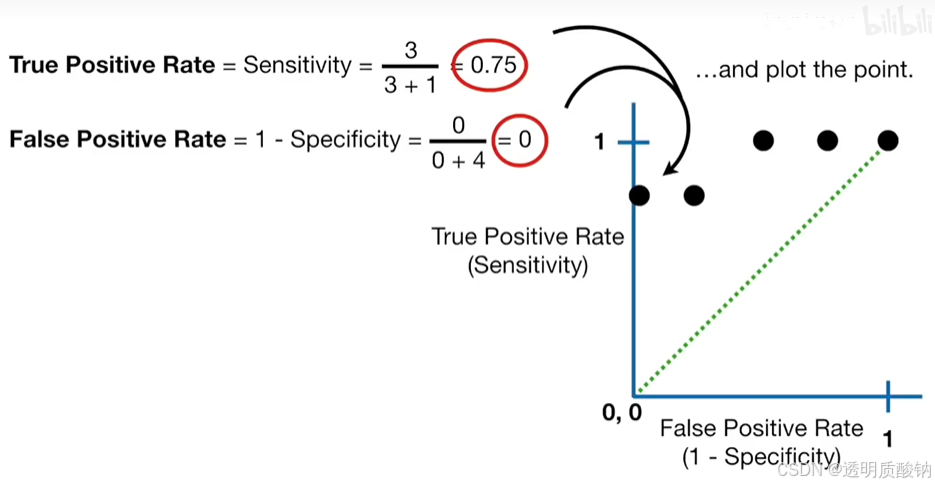
继续提高阈值,
如上图,新点表示的阈值正确分类75%的肥胖样本和100%非肥胖的样本。
换句话说,这个阈值不会导致假阳性
继续提高阈值,
最后我们选择一个阈值使得所有样本都被归类为非肥胖
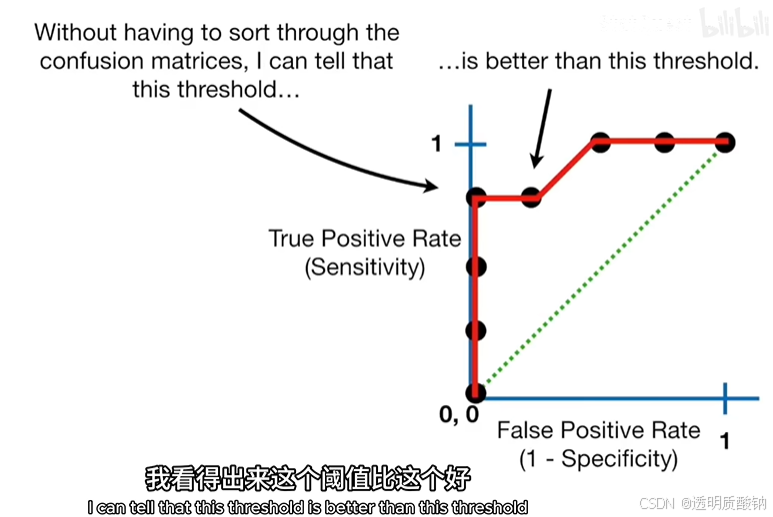
我们可以把这些点联系起来,这给了我们一个ROC图,如下图
ROC图总结了由每个阈值产生的所有的混淆矩阵,且无需盘点每个混淆矩阵就能看出某个阈值比另一个阈值更好
且这个ROC的最佳阈值就在两个点中产生
Area Under the Curve
接下来谈谈 曲线下面积AUC(Area Under the Curve)
AUC使比较两条ROC曲线变得容易
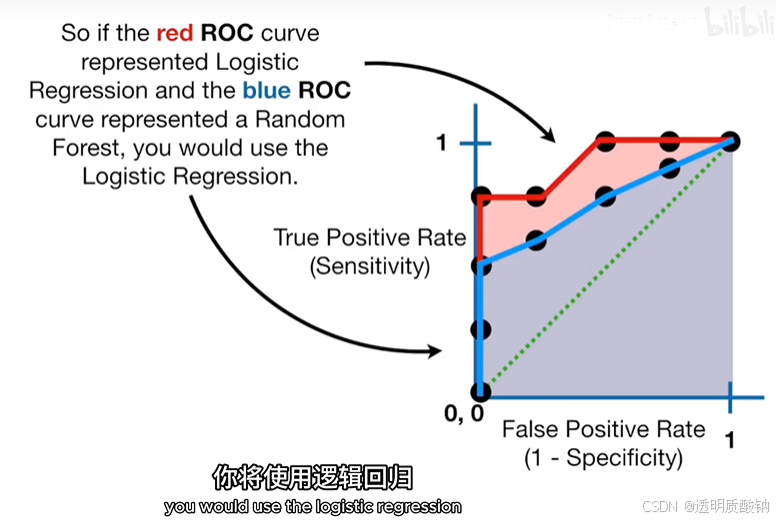
这里红色的AUC是0.9
红色ROC曲线的AUC大于蓝色ROC曲线的AUC,说明红色曲线更好。所以如果红色ROC曲线代表逻辑回归,蓝色的ROC曲线代表一个随机森林模型,你将使用逻辑回归
虽然ROC图的绘制使用了真阳性率和假阳性率来总结混淆矩阵,还有其他指标可以做同样的事情
例如,人们经常把真阳性率替换为精确度
精确度 = 真阳性 / (真阳性 + 假阴性)
精确度表示多大比例的阳性样本被正确分类
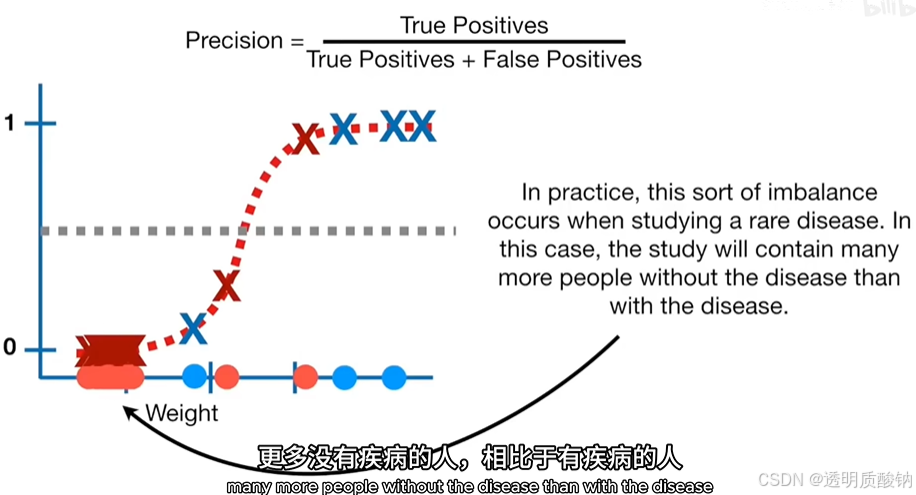
如果相对于肥胖样本的数量,有很多非肥胖的样本。那么精确度可能比假阳性率更有用。这是因为精确度在其计算中不包括真阴性的数量,并且不受不平衡数据的影响
在实践中,这种数据不平衡会发生在研究一种罕见疾病时,在这种情况下,这项研究将包含更多没有疾病的人,相比于有疾病的人
概括地说,
当设置不同阈值时,可以得到不同混淆矩阵,而每个混淆矩阵对应一个TPR值和FPR值。如果把所有的TPR值和FPR值映射到一个二维空间中,然后把这些点连起来,就可以得到ROC曲线
ROC曲线使得用于做决定的最佳阈值变得容易。AUC可以帮你决定哪种分类方法更好
ROC曲线 & AUC值
假设有一个分类器可以判断一张图片是否是汉堡,那么分类器会先计算这张图片是汉堡的概率,进而预测到底是否是汉堡
每个阈值会对应一个混淆矩阵
那么,有没有一种方法能把所有的混淆矩阵表示在同一个二维空间内呢?
——Receiver Operator Characteristic(ROC)曲线
对于一个混淆矩阵,可以求出TPR和FPR两个指标。如果把TPR作为y轴、FPR作为x轴,就可以把每个混淆矩阵和这个二维矩阵中唯一的一个点对应
判断哪个分类器效果更好?
TPR和FPR的分母,对于同一个数据集是固定不变的,
由于我们希望TP尽可能大、FP尽可能小,也就是说我们想要TPR尽可能大、FPR尽可能小
因此曲线越靠近左上角,效果越好
那么我们能否通过一个数值来看,而不是单纯通过图片呢?
——曲线与x轴的面积,也就是AUC值
AUC的值在0-1之间,越大越好
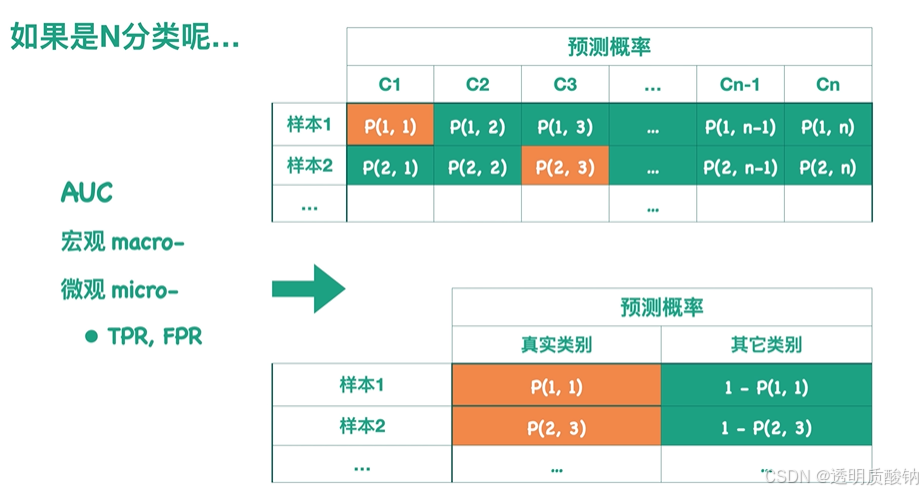
多分类
对于多分类,可以求得宏观macro和微观micro的AUC
求宏观macro AUC:
针对每一个类别都可以画一个ROC曲线,然后求出对应AUC值。然后对每一个类别的AUC求某种平均就得到了整个模型宏观的AUC值
求微观micro的AUC:
假设概率预测结果如下表所示,
例如样本1的真实类别为C1,样本2的真实类别为C3。
每行概率之和为1,因此我们可以得到一个经过转换的预测结果。可以根据这个表得到针对整个模型的ROC曲线,以及它对应的AUC值
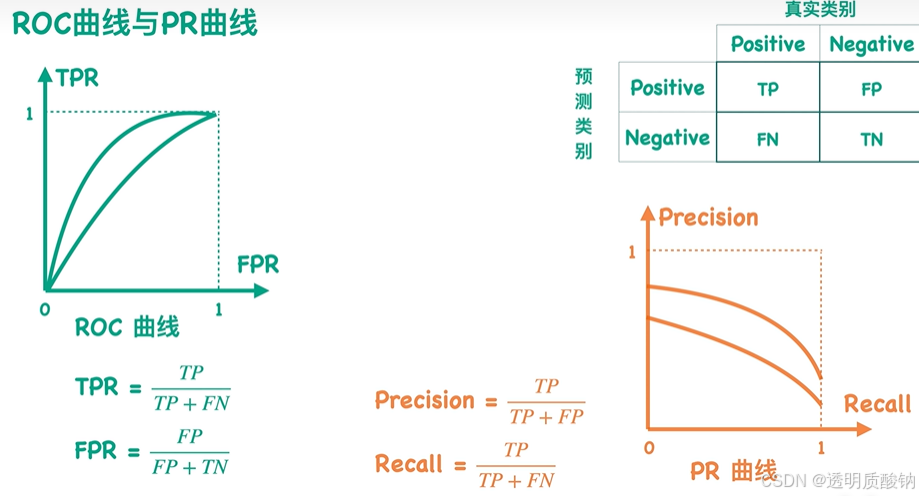
ROC曲线 & PR曲线
现在如果我们用Precision值来代替前面ROC曲线中的TPR值,用Recall值来代替FPR值。并且将这些点连起来得到一个新的曲线,就是PR曲线,也就是Precision-Recall曲线
因为对于每一个混淆矩阵,都有唯一的TPR值-FPR值的数值对,也可以计算出唯一的Precision值-Recall值的数值对,所以可以说:每一个ROC曲线都有唯一的一个PR曲线与之对应,也就是它们之间可以相互转换,且是一一对应的
上一节中提到ROC曲线越靠近左上角效果越好
而对于PR曲线而言,因为是希望Precision和Recall值同时越大越好,所以 PR曲线越靠近右上角效果越好
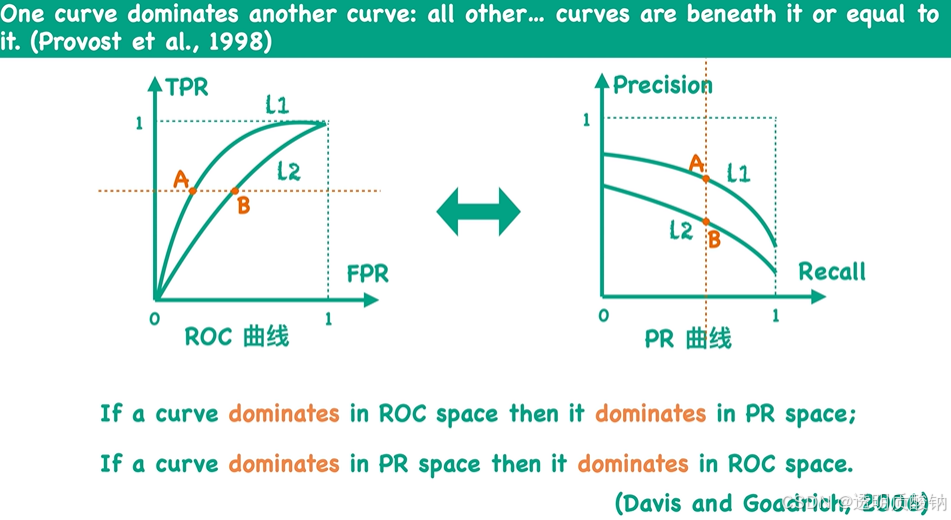
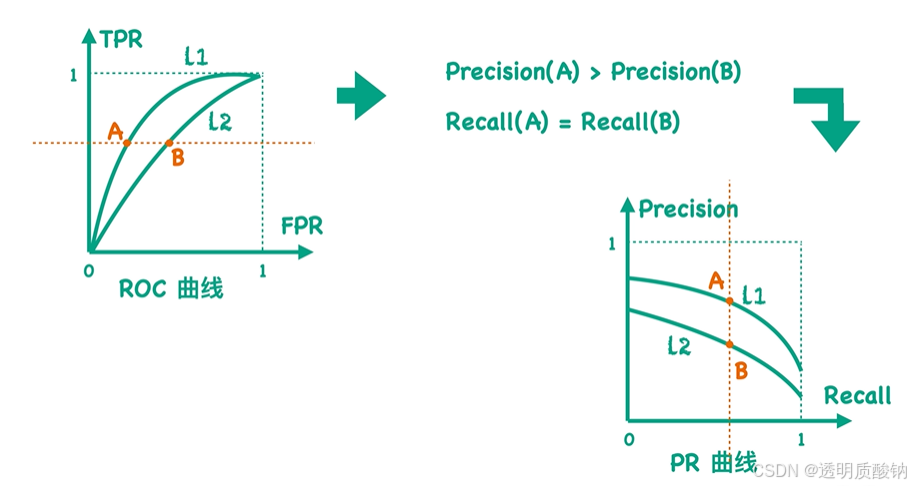
ROC曲线与PR曲线的关系
ROC曲线与PR曲线有什么关系呢?
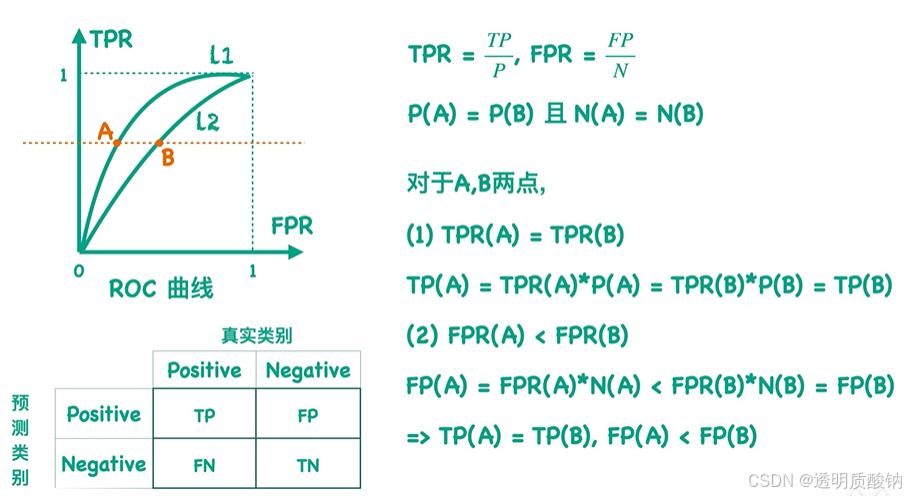
L1曲线 dominates L2 -> L1曲线上所有点都在L2曲线上方
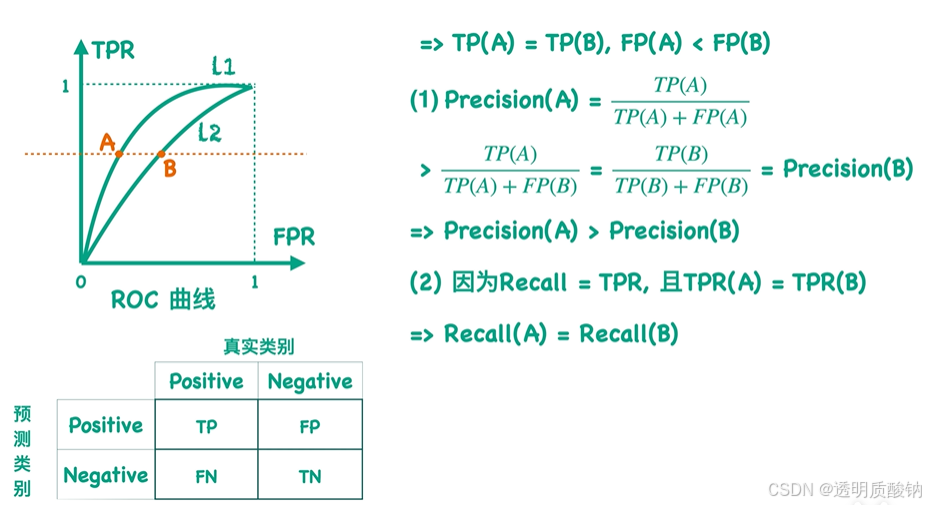
证明上述结论:
得到了AB之间Precision、Recall值的关系后,再代入到PR曲线中:
就可以判断出在Precision中L1也dominatesL2
ROC曲线与PR曲线应用场景
ROC曲线与PR曲线分别在什么情况下使用?
如上图,根据定义可知, TPR值等于Recall值
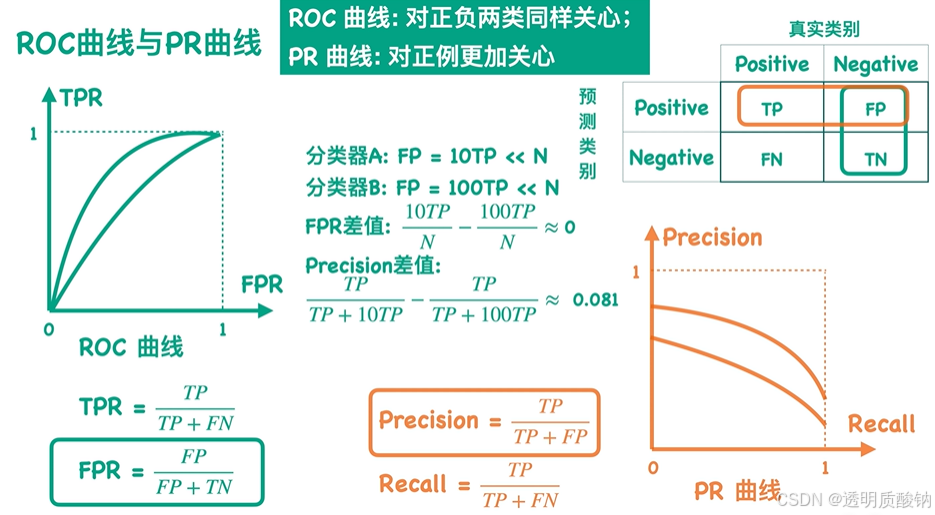
因此这两个曲线最大的区别就是FPR值和Precision值
如上图,假设同一个数据集有两个分类器,因此两个分类器的TP值和FN值都是相同的
可以看出,当FP值不同时,Precision值更能反应两个分类器的差异
因此得出结论:
ROC曲线:对正负两类同样关心;
PR曲线:对正例更加关心
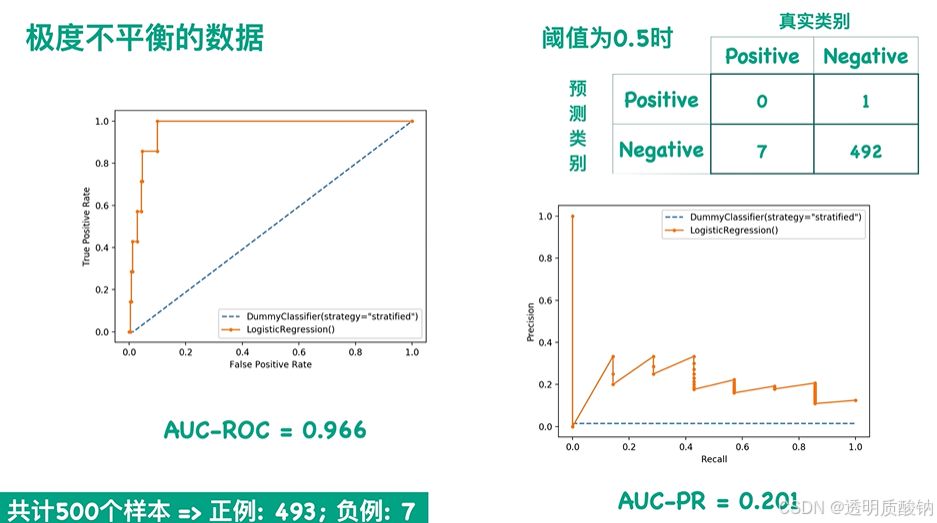
下面来更直观地看一个例子,极度不平衡的数据
从左边的ROC图看起来效果很好,但从右边的PR图看起来效果很差
(注意这里图片左下角错了,是493个负例)
如果我们更关心正类的预测结果,且数据非常不平衡时,我们应选用PR曲线而不是ROC曲线
AUROC & AUPR
(1)AUROC
AUROC即为area under ROC curve,意为ROC 曲线下面积。在前面有提到曲线越靠左上代表模型表现能力越好,代表着曲线的面积也越大,即AUROC数值越高模型表现能力越好。
(2) AUPR
AUPR 即为area under Precision-Recall curve,意为在横轴为Precision 纵轴为Recall所绘出的曲线,通常会希望Precision 及Recall都是高的,所以曲线越靠近右上代表模型表现能力越好,相同的AUPR数值越高代表模型能力也越好。
结语: 模型的好坏不单单只是看训练的准确率,更应该关注在模型的泛化能力,那以上的评估指标就相当的重要。
Reference
【官方双语】ROC & AUC 详细解释!
【小萌五分钟】机器学习 | 模型评估: 准确率 Accuracy 精确率 Precision 召回率 Recall F1值