一.定义
割点:设G是一个连通无向图,G的衔接点(关节点、割点、割顶,下面让我们忽略掉这些奇奇怪怪的定义和名称,只追求自洽,并且只讨论连通无向图)指G中一个节点,删除该节点将导致图不连通。
重连通图:没有割点的连通图。
&&等价定义:或者只含一个点,或者只含两点一边(特殊情况以后只在有必要的时候提到),或者是这样的图,任意一对顶点间存在两条不相交(除起点和终点)的初级通路。
其中任意一对顶点间存在两条不相交(除起点和终点)的初级通路也可以表述为,任意两个点处在一个初级回路上。
等价定义->定义
如果图符合等价定义,删除其中任意一个顶点,考虑剩余任意一对顶点,如果删除的顶点不在通路上,那么两顶点依然连通;如果顶点在其中一条通路上,那么由于通路不相交,这个顶点不属于另一通路,两顶点依然连通;符合定义。
定义->等价定义
如果图符合定义,删除其中任意一个顶点,考虑剩余任意一对顶点,设起初这对顶点之间存在一条初级通路t,因为可能删除t上的顶点,那么这对顶点必须存在另一条初级通路s,并且,由删除点的任意性,s不能包含t中的顶点(除起点和终点),所以顶点间存在两条不相交的初级通路。符合等价定义。
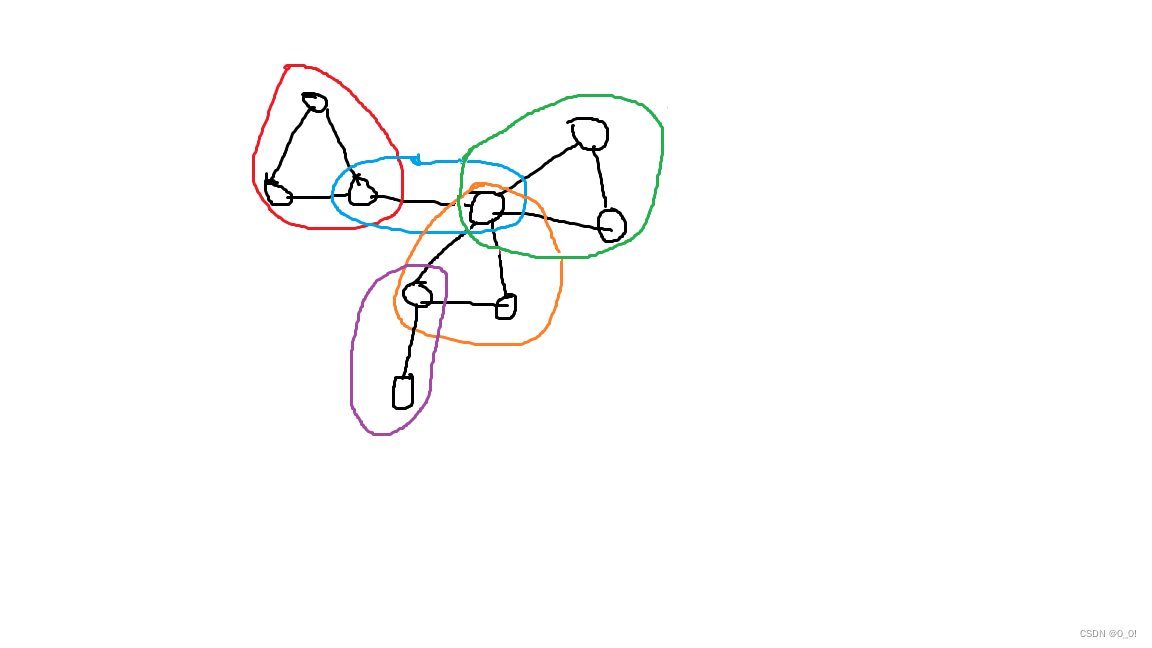
点双(点双连通分量):极大重连通子图;
二
各种性质/定理
白色路径定理:不是重点,可以自行百度
定理1:在对无向图的dfs中,从来不会出现横向边。
设(u,v)是图中任意一条边,不妨设先发现u。根据白色路径定理(在我另一篇有提到,可以去百度),u是v的祖先。(或者这样理解,先进行u的dfs,因为v未被访问,所以在u退出dfs前,一定会访问v),所以边要么是前向边,要么是树边,要么是后向边。(因为后向边和前向边、树边重合,所以以下只会讲树边和回边)
性质1:两类割点
1.若生成树的根有两棵或以上的子树,则此根必为割点,如A(由定理一,子树之间无边)
2.若生成树中某个非叶子顶点v,其某棵子树到祖先没有回边,则v是割点,如B,D.
如果不属于以上情况,则不是割点。
性质2:两个点双最多有一个公共点,如果有,一定是割点。
如果存在两个公共点,删除其中一个公共点后,由点双定义,点双到另一公共点之间仍连通,因而非公共点之间可以通过公共点连通,两个点双组成的图会包含原点双,原点双与定义矛盾。如果只有一个公共点,删去后非公共点也不应该连通,所以是割点。
性质3:除非点双是一个连通分支(孤岛),那么它与其他点双必有公共点。
如果点双不是孤岛,那它一定会伸出一条边(u,v),这条边可能是点双,我们可以通过不断扩展形成点双。该点双不会是原点双(存在不同的点v),u为公共点。
性质4:两个点双间不存在直接的(不经过其他点双的边)初级通路,即点双只能通过公共点直接连接。
假设存在,扩展路径上的一条边,会形成新点双。
性质5:非公共点不是割点。
删除非公共点,由点双定义,点双到公共点之间仍连通,因而相邻点双非公共点之间可以通过公共点连通。
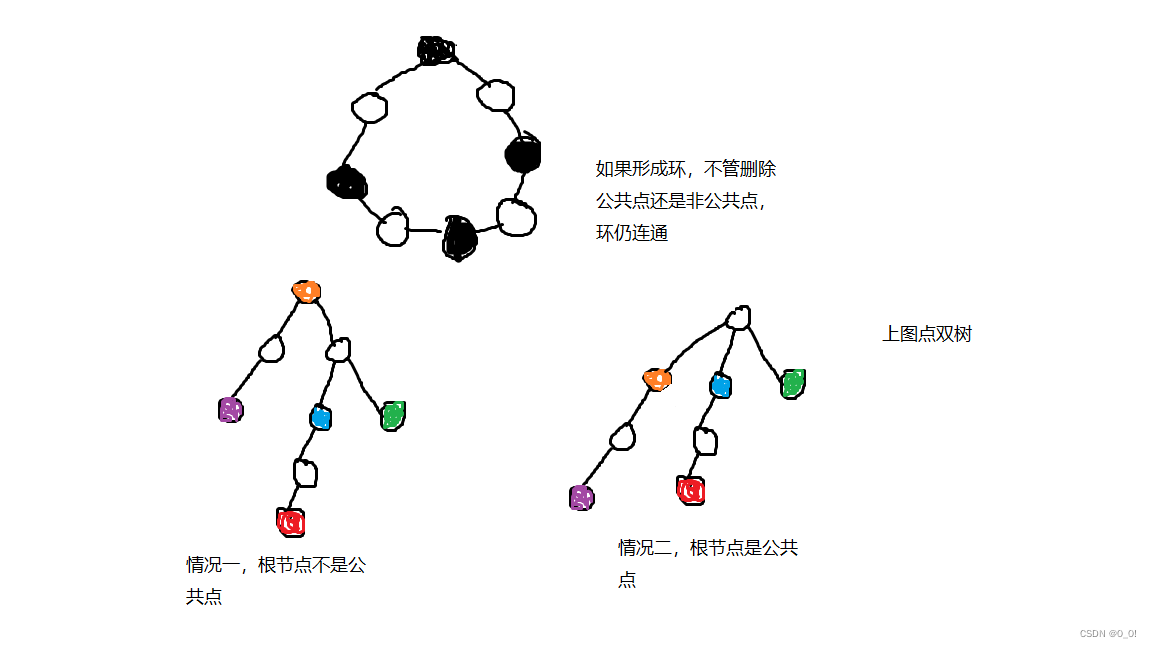
性质6:点双树
因为点双之间通过公共点连接,为了使点双之间有更明显的界面,我们虚设一个点,称为虚点,让
公共点都连接到这个虚点上,从而点双被间接连通,相应的,我们把分离出的点双叫做实点。
这样形成的图便形成了实-虚-实结构。
可以证明,这样的图不会存在环,否则不管删除公共点(在图上还得再删除相应虚点)还是删除非公共点,环上点仍连通,因为环包含点双,这样会与点双定义矛盾。
又因图的连通性,因此这样构造的图是一棵树,我把它称为点双树(bcTree);我们以第一个访问的点为树根(如果是非公共点用点双代替),会出现两种情况,根可能是实点,也可能是虚点。
更新:最近在网上看到了圆方树,好像这个跟那个有点像,不过我也看不大懂。
画成有向树的形式可能具有误导性,它更适合作为一棵无向树。
三
1.求割点
由性质1已经可以有方法求出割点
对于非根节点,我们要判断其子树到祖先由没有回边。
有没有边很好判断,关键判断是到祖先的边,dfs栈中自己之前的就是祖先了。也就是栈中访问时间要早的点,我们可以设置数组dfn(时间)和ins(是否在栈),这样求割点的时间复杂度也就是dfs的时间复杂度。(有待实验……又想了下,这样只能判断某个特定点,不可行)
tarjan给了一个类似求强连通分量的方法
设置数组low表示访问到的(dfs过程中遇到的,包括自己)最早节点,如果顶点v子树low[i]<dfn[v],因为没有横向边,则子树到祖先有回边,否则没有。
low[v]=min{low[i],dfn[v],dfn[k]}(i孩子,k祖先)
对于根节点,我们判断其子树棵数,我们可以做标记来求。也可以先访问自己,再对孩子dfs,看第个孩子能不能访问所有点,或者看有几个孩子做了dfs。
代码可以去网上搜。
2.求点双
网上好像有一种用差分结合dfs求的方法,这里我们还是讲tarjan算法。
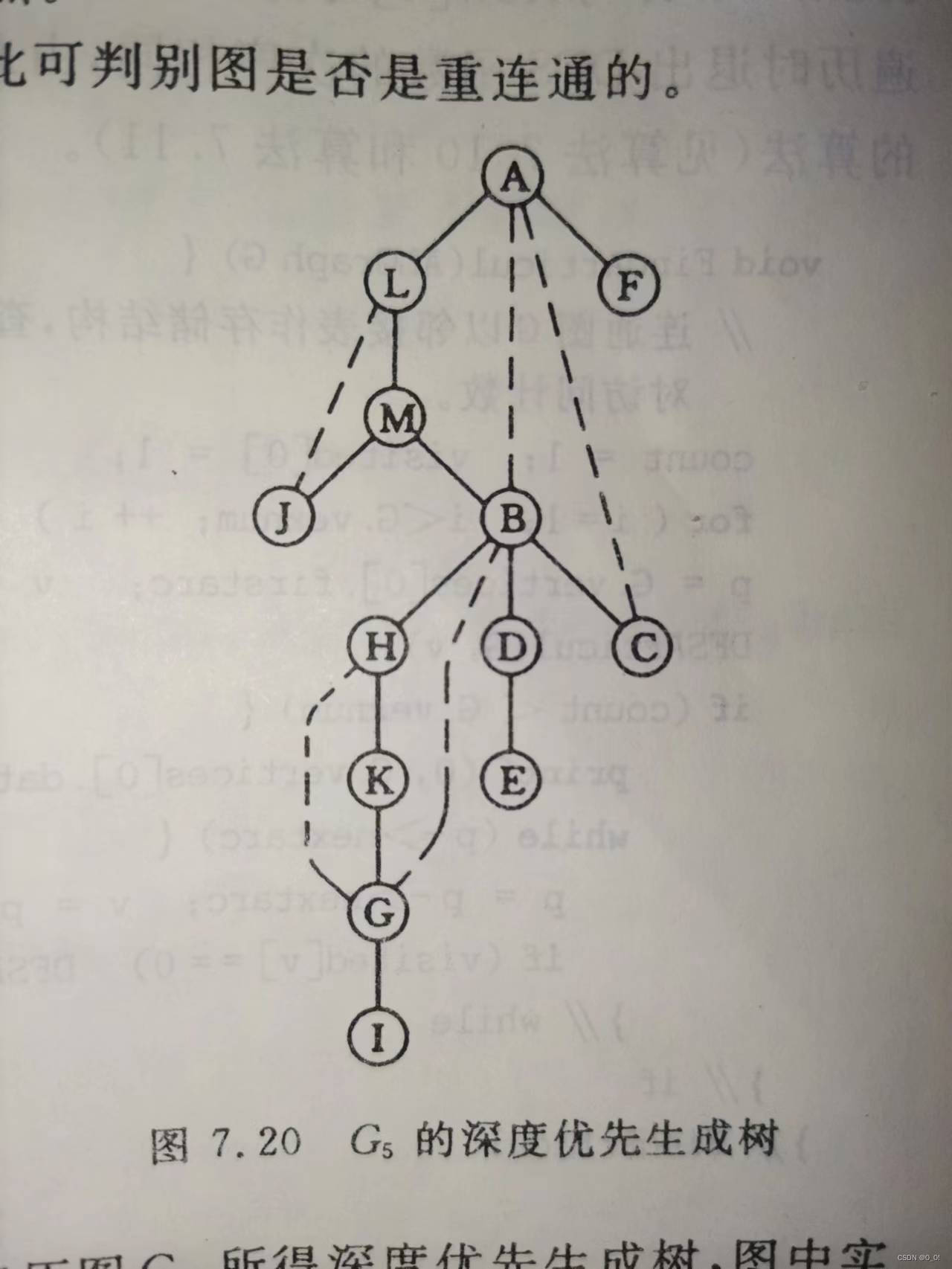
结合图一的深度优先生成树。
1.对于非根节点,因为割点割断是无回边子树和父亲的路,所以点双不能同时包含割点和父亲。这样一来,我们在以割点为界的树tree(包括回边,这棵树的根是割点,有孩子的叶子也是)中寻找点双,由性质1,考虑树中每个非叶子节点(除根),可以得到删除它它的无回边子树仍与根连通。同时,不管点双是否包含tree的根,它不应该同时包含不同子树的点。
因此树tree的根和任一棵无回边的子树是点双。而且满足完备性(不存在其他包含这些树中点的点双)。摘出点双后,割点也就不再是割点。
2.上面的陈述你可能一时半会捋不清,我们通过一个性质从另一个角度来求点双。
性质7:点双是某个割点的后代(除第一个被访问的)
因为点双通过割点连接,除第一个被访问的点双,其他点双第一个被访问的结点一定是割点。根据白色路径定理这个割点是点双中其他点的祖先。
性质8:割点是某个点双的祖先
从以第一个被访问的点双为根的点双树上看,虚点一定是某个实点的祖先。相应的割点是某个点双的祖先。也可以利用点双树看出性质7;
因此,我们找到了割点,也就找到了一棵树,在这棵树里会存在点双。如果你看了我另一篇讲强连通分量的blog,你就知道接下来该干嘛。
如果不清楚,可以看看点双树,为了每次摘的实点都是叶子,我们可以根据割点孩子(割点可能有多个点双子树)退出dfs的顺序来摘,这时孩子的割点子树已经退出dfs;因为点双间通过公共点连通,若割点树中没有其他公共点,那么割点的每棵子树只能属于一个点双,任意两棵会不会属于同一点双呢,因为无横边,割点会割开子树,所以一个点双属于一棵子树(再加上割点,第一个访问的点)。
具体做法,设置一个栈用来存搜索树,若父亲是割点,摘无回边子树(那棵判断父亲为割点的树,出栈)。
在图3第一种情况下,最后可能还剩下个点双,也出。
代码的话去网上搜吧
相关信息见
《算法导论》第三版 p354,p360
《数据结构》严蔚敏 p176