AVL树
1.AVL树初识
(1)定义
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
它的左右子树都是AVL树;
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1);
总的来说:AVL树是一颗高度平衡的二叉搜索树,它通过平衡因子来对结构进行控制,保证树结构不会出现单边这种极端情况
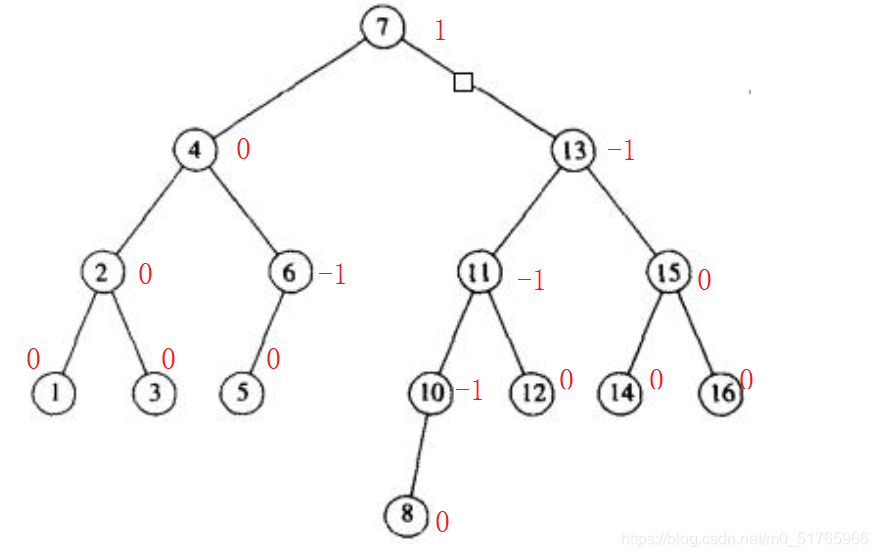
示意图:
(2)优缺点
优点是查找的时间复杂度为O(logN),n为节点个数;
缺点是插入和删除的效率低
(3)适用场景
AVL树的插入和删除都需要进行结构的调整,因此不适合进行大量的插入和删除操作,适用于初始状态就插入数据,后面只进行频繁的查找操作的场景
2.AVL树的核心操作及实现思路
(1)AVL树的数据结构
树节点的定义
//节点
template<class T>
struct AVLNode{
T _val;//节点存储的数据
int _bf;//平衡因子:右子树高度减去左子树高度
AVLNode<T>* _parent;//父节点
AVLNode<T>* _left;//左孩子
AVLNode<T>* _right;//右孩子
AVLNode(const T& val)
:_val(val)
, _bf(0)
, _parent(nullptr)
, _left(nullptr)
, _right(nullptr)
{}
};
树的定义
template<class T>
class AVLTree
{
private:
typedef TreeNode<T> Node;
Node* _root; //根节点
};
(2)节点的插入
先找到合适的位置,插入节点;
再进行平衡因子的调整;
平衡因子的调整有以下四种情况:
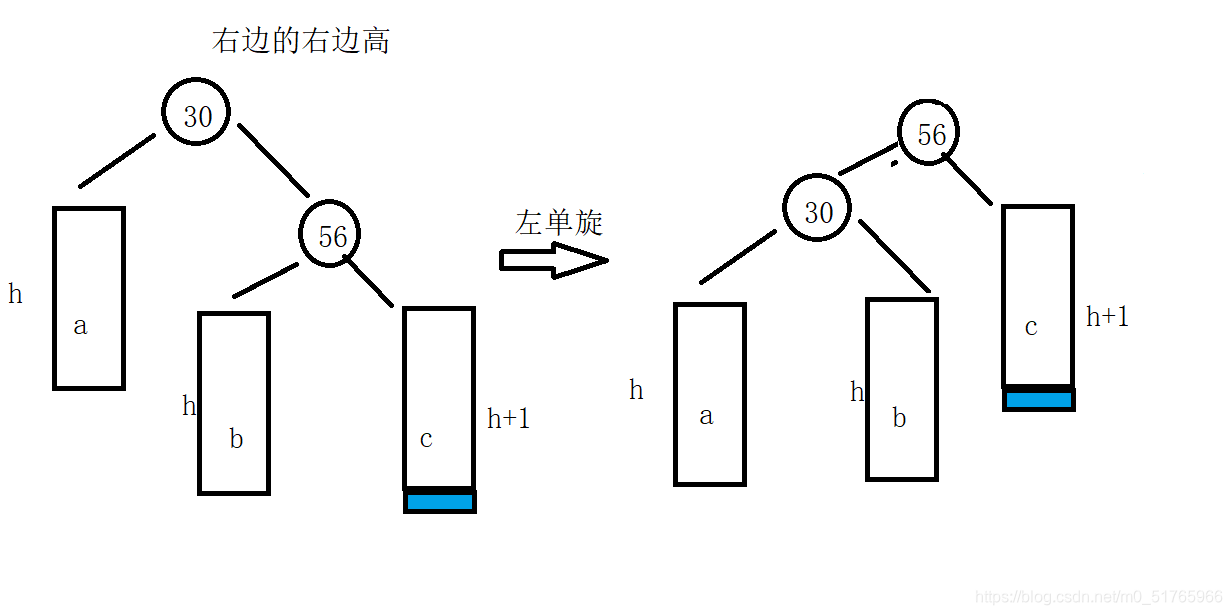
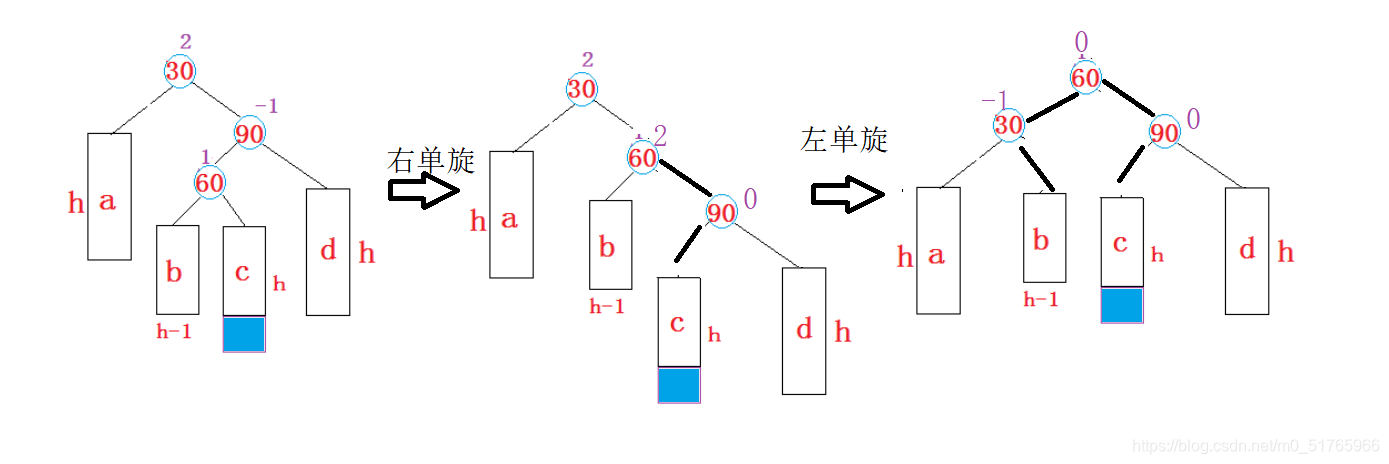
a.右边的右边高,左单旋
右边的右边高,将根节点拉下来,让右孩子成为新的根节点,并进行结构的调整使其满足AVL树的性质
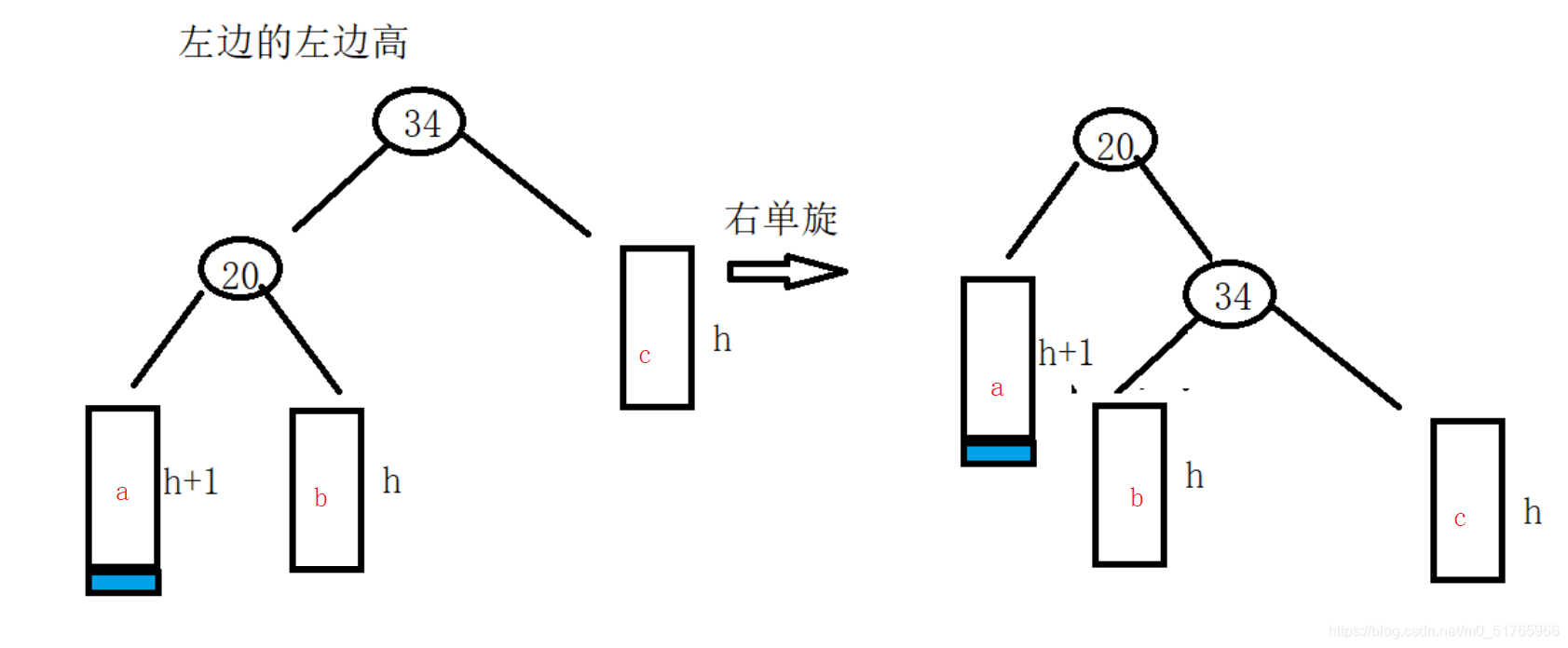
b.左边的左边高,右单旋
左边的左边高,将根节点拉下来,让左孩子成为新的根节点,并进行结构的调整使其满足AVL树的性质
c.左边的右边高,先左旋再右旋
先进行局部调整,让不平衡的集中到同一侧,再整体进行调整
d.右边的左边高,先右旋再左旋
先进行局部调整,让不平衡的集中到同一侧,再整体进行调整
关于平衡因子修正问题的理解
当进行双旋时,不能直接对parent和curNode的平衡因子置为0,需要根据实际情况进行计算
-
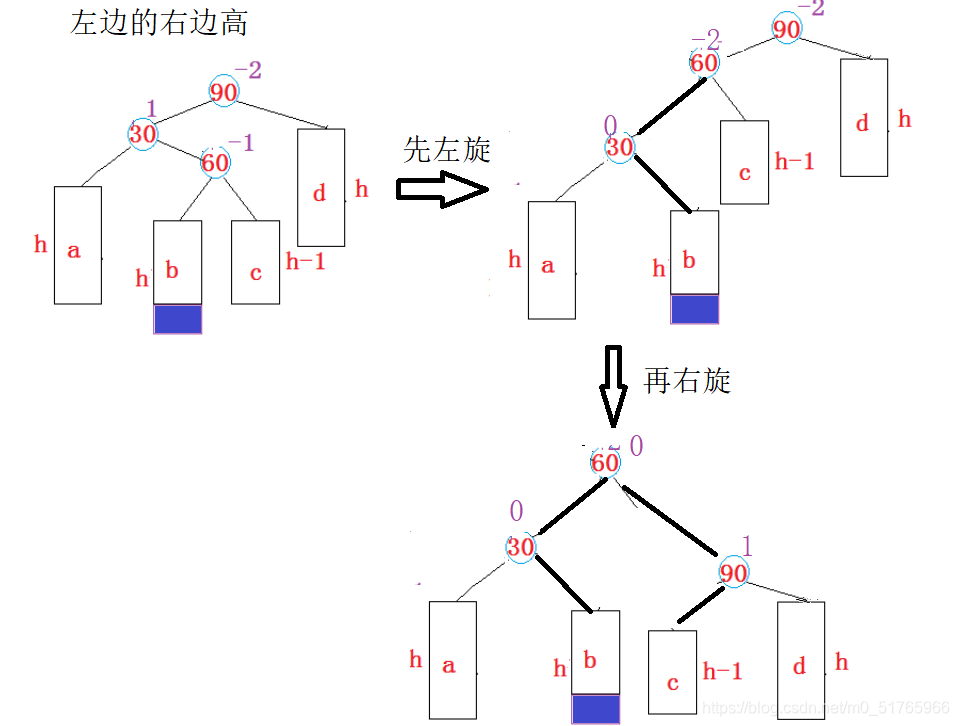
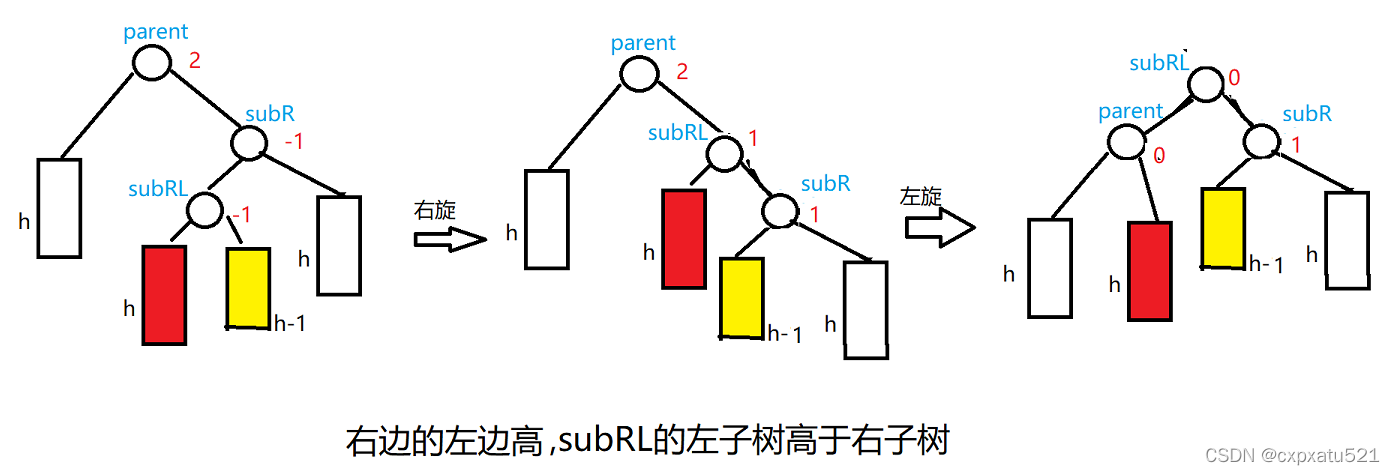
右边的左边高,进行右左双旋
情况1:subRL的左子树高于右子树
subRL的左子树高于右子树,即subRL->_bf = -1;
subRL的左子树在进行双旋之后会被调整到parent的右边,parent的左右两边高度相等,因此parent的平衡因子为0;
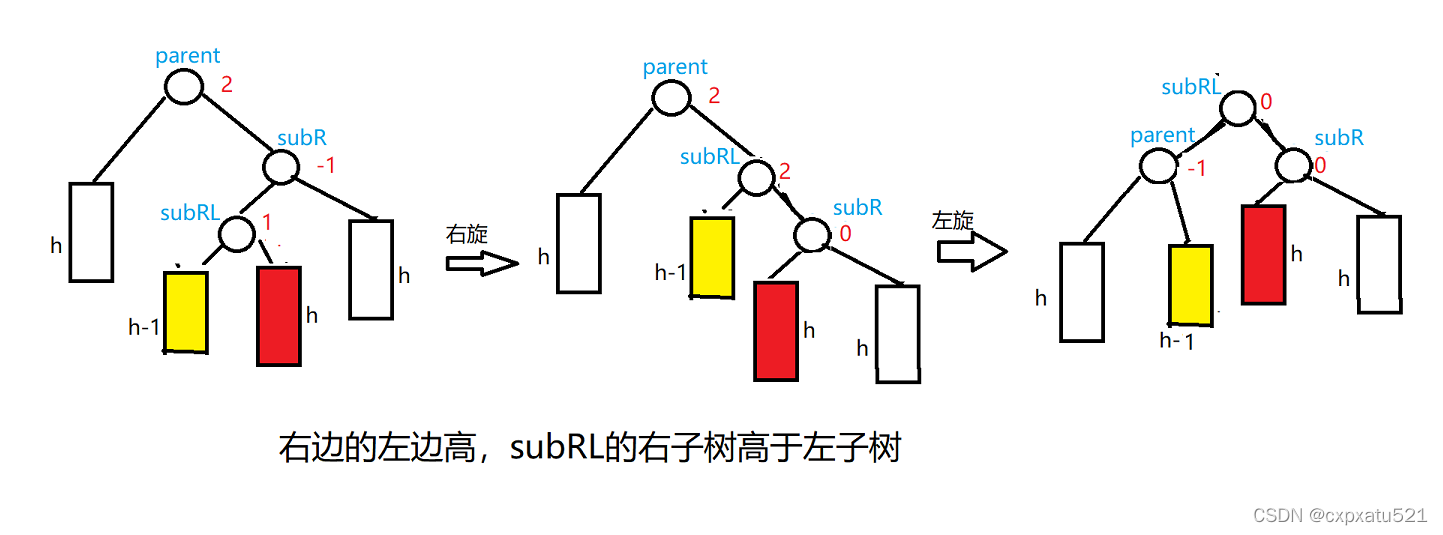
subRL的右子树在进行双旋之后会被调整到subR的左边,subR的左子树高度低于右子树高度,因此subR的平衡因子为1情况2:subRL的右子树高于左子树
subRL的右子树高于左子树,即subRL->_bf = 1;
subRL的左子树在进行双旋之后会被调整到parent的右边,parent的左边高度高于右边高度,因此parent的平衡因子为-1;
subRL的右子树在进行双旋之后会被调整到subR的左边,subR的左右子树高度相同,因此subR的平衡因子为0 -
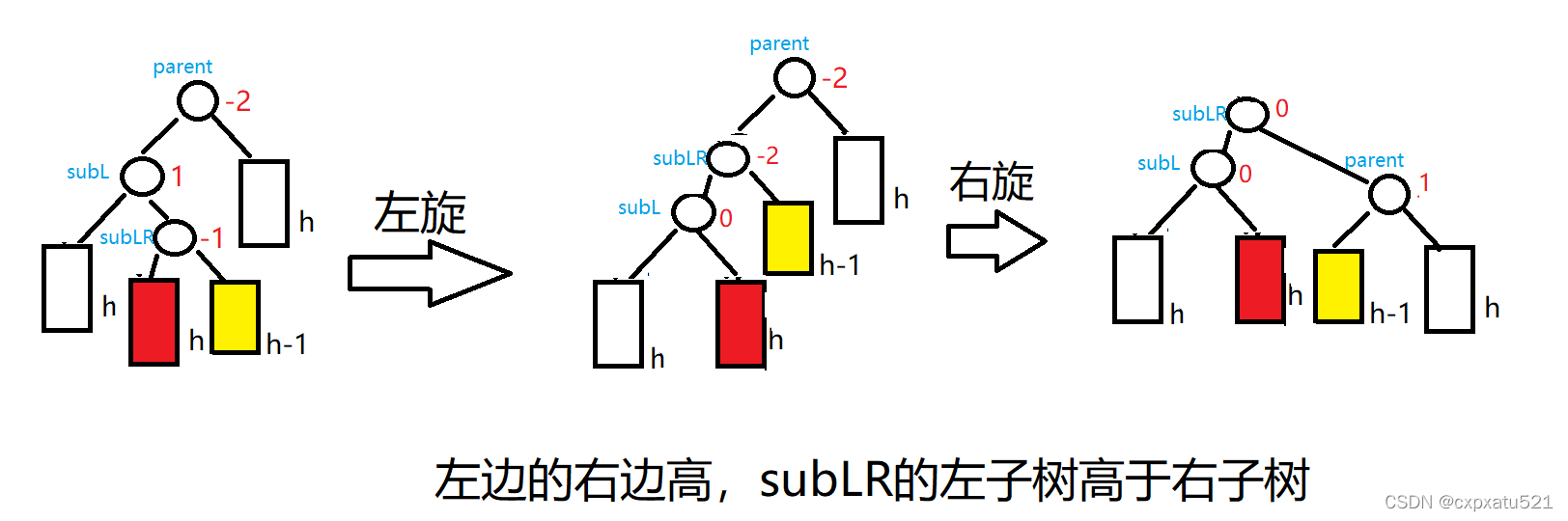
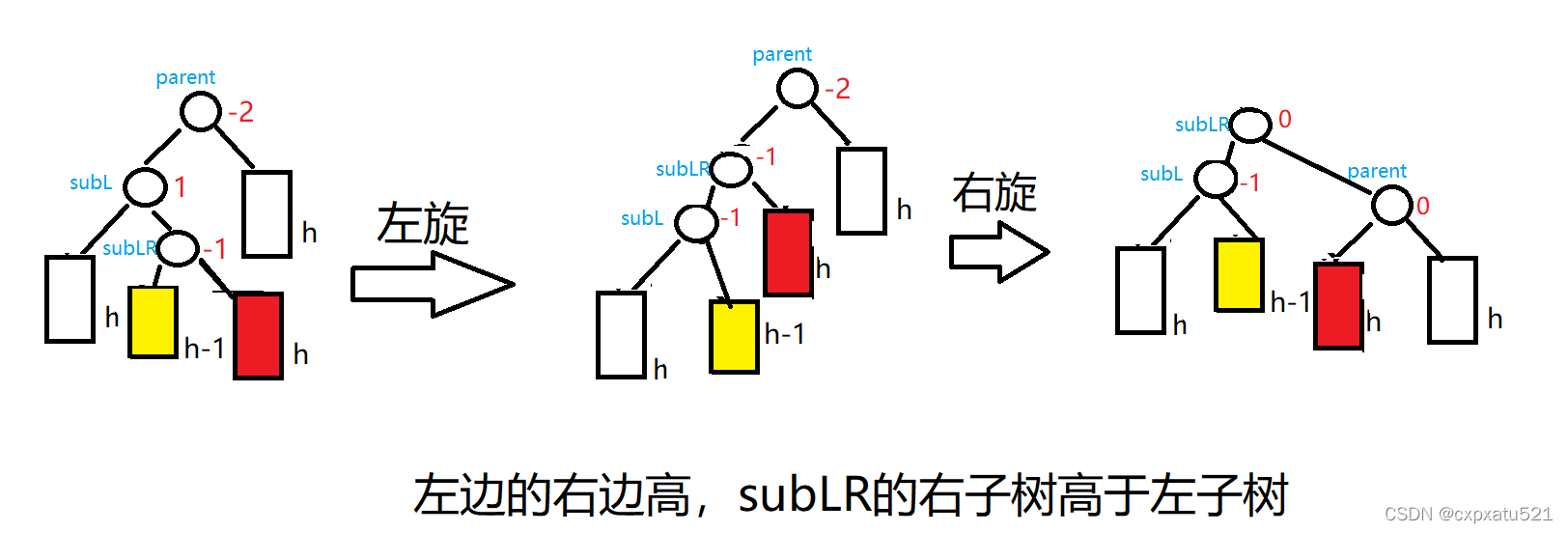
左边的右边高,进行左右双旋
情况1:subLR的左子树高于右子树
subLR的左子树高于右子树,即subLR->_bf = -1;
subLR的左子树会被subL的右边,subL的左右子树高度相等,因此subL的平衡因子为0;
subLR的右子树会被放到parent的左边,parent的左边低于右边,因此parent的平衡因子为1;情况2:subLR的右子树高于左子树
subLR的右子树高于左子树,即subLR->_bf = 1;
subLR的左子树会被subL的右边,subL的左边高于右边,因此subL的平衡因子为-1;
subLR的右子树会被放到parent的左边,parent的左右两边高度相等,因此parent的平衡因子为0;
(3)节点的删除
删除节点的步骤:
- 找到要删除的节点;
- 将节点从AVL树中删除;
- 进行平衡因子的调整,使之符合AVL树的结构特性
待删除节点的四种状态及其对应的删除策略
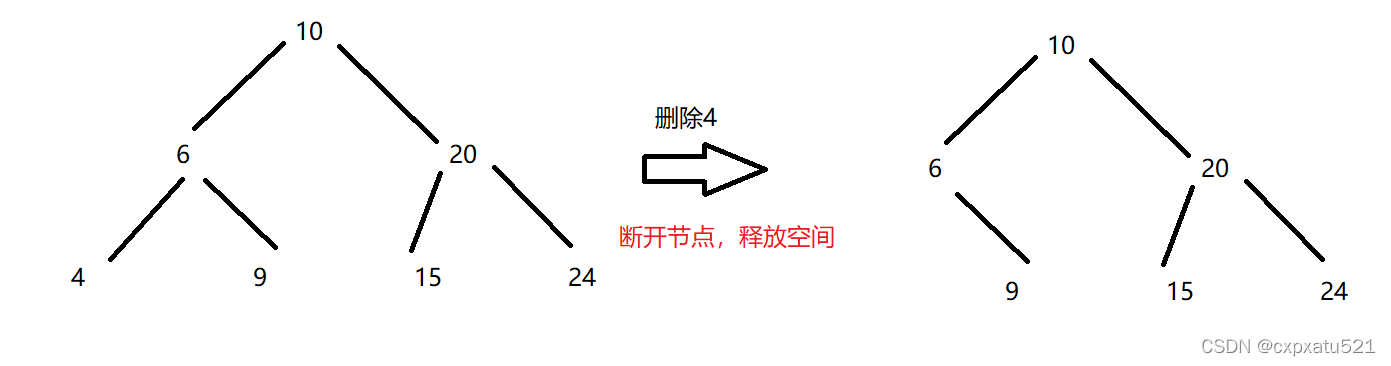
a.待删除节点没有左右孩子
将节点从树中断开,释放节点空间
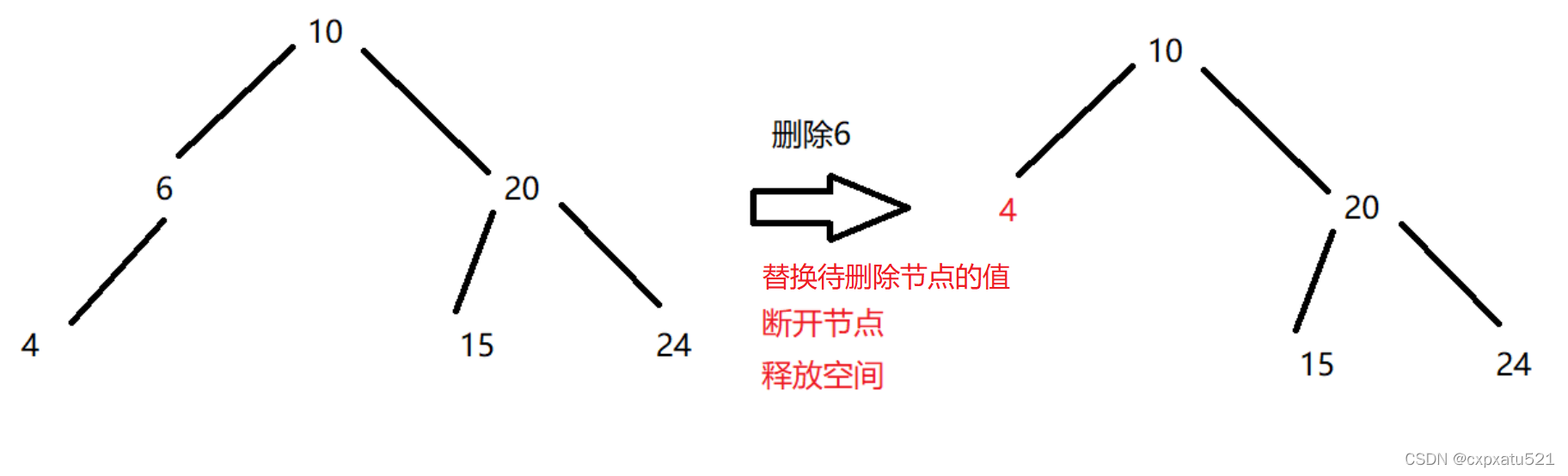
b.待删除节点只有左孩子
将待删除节点的值替换为它的左孩子的值,将左孩子节点从树中断开,释放节点空间
c.待删除节点只有右孩子
将待删除节点的值替换为它的右孩子的值,将右孩子节点从树中断开,释放节点空间
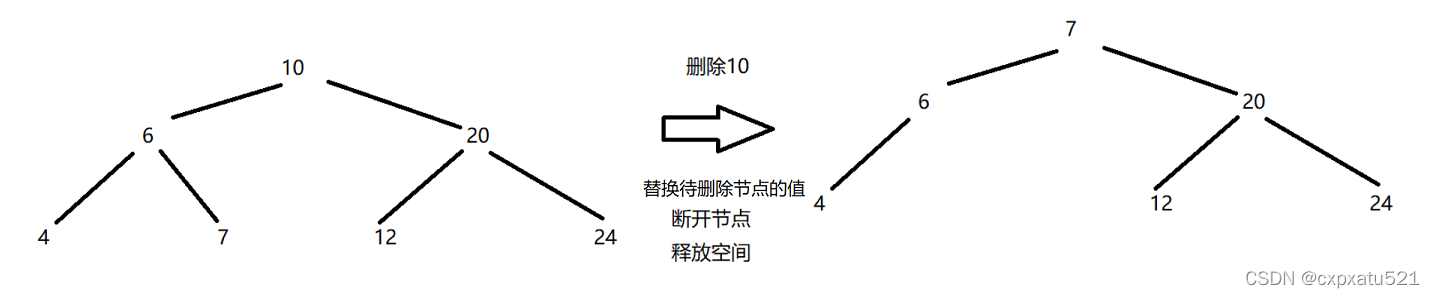
d.待删除节点左右孩子都存在
将待删除节点的值替换为它的前驱节点(中序遍历的前一个节点,也就是左子树的最右节点)或者后继节点的值(中序遍历的下一个节点,也就是右子树的最左节点),我采用的是前驱节点;
将前驱节点从树中断开,释放节点空间;
删除之后结构的调整
AVL树在删除节点之后,需要向上调整平衡因子,父节点的平衡因子的值需要根据左右子树的高度进行计算,如果父节点的平衡因子的绝对值大于1,此时不满足AVL树的结构特性,需要进行旋转,旋转之后同样需要向上继续调整直到根节点。
(4)判断是不是AVL树
根据两方面进行判断,一是能否满足二叉搜索树的性质,二是能否满足平衡的性质
判断是否为二叉搜索树,可以判断中序序列是否递增来得到;
判断是否平衡,可以根据左右子树高度差的绝对值是否小于等于1,并且左右子树同时平衡来得到
3.AVL树模拟实现源码
#pragma once
#include <stdlib.h>
#include <stack>
#include <queue>
#include <iostream>
using std::stack;
using std::queue;
using std::cout;
using std::endl;
//AVL树节点
template<class T>
struct TreeNode
{
T _val;
int _bf;
TreeNode* _parent;
TreeNode* _left;
TreeNode* _right;
TreeNode(const T& val)
:_val(val)
, _bf(0)
, _parent(nullptr)
, _left(nullptr)
, _right(nullptr)
{}
};
//AVL树
template<class T>
class AVLTree
{
private:
typedef TreeNode<T> Node;
Node* _root;
public:
AVLTree()
:_root(nullptr)
{}
~AVLTree()
{
Destroy(_root);
}
//插入数据
bool Insert(const T& val)
{
//1.执行二叉搜索树的插入操作
if (!_root)
{
_root = new Node(val);
return true;
}
//1.1:寻找插入位置
Node* parent = nullptr, * curNode = _root;
while (curNode)
{
if (val > curNode->_val)
{
parent = curNode;
curNode = curNode->_right;
}
else if (val < curNode->_val)
{
parent = curNode;
curNode = curNode->_left;
}
else
{
//不允许出现重复节点
return false;
}
}
curNode = new Node(val);
//要插入的节点的值小于父节点的值,插入父节点的左边
if (val < parent->_val)
{
parent->_left = curNode;
}
//要插入节点的值大于父节点的值,插入父节点的右边
else
{
parent->_right = curNode;
}
curNode->_parent = parent;
//2.进行平衡因子的调整
while (parent)
{
if (parent->_left == curNode)
{
--parent->_bf;
}
else
{
++parent->_bf;
}
//新插入的节点将将较低的子树补齐了
if (parent->_bf == 0)
{
break;
}
//原树平衡,新插入的节点打破了平衡,向上继续调整平衡因子
else if (parent->_bf == 1 || parent->_bf == -1)
{
curNode = parent;
parent = curNode->_parent;
}
//平衡因子绝对值大于1,进行结构调整
else if (abs(parent->_bf) == 2)
{
if (parent->_bf == 2 && curNode->_bf == 1)
{
//右边的右边高,进行左单旋
RotateL(parent);
}
else if (parent->_bf == 2 && curNode->_bf == -1)
{
Node* subRL = curNode->_left; //当前节点的左孩子
int bf = subRL->_bf;
//右边的左边高,先右旋再左旋
RotateR(curNode);
RotateL(parent);
//进行平衡因子的修正
//subRL左右子树高度的不一致会影响parent和curNode的平衡因子
//subRL的右子树会被放到curNode的左孩子位置,而subRL的左孩子会被放到parent的右孩子位置
if (bf == 1)
{
parent->_bf = -1;
curNode->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 0;
curNode->_bf = 1;
}
}
else if (parent->_bf == -2 && curNode->_bf == -1)
{
//左边的左边高,右旋
RotateR(parent);
}
else if (parent->_bf == -2 && curNode->_bf == 1)
{
Node* subLR = curNode->_right;
int bf = subLR->_bf;
//左边的右边高,先左旋再右旋
RotateL(curNode);
RotateR(parent);
//进行平衡因子的修正
//subLR左右子树高度的不一致会影响parent和curNode的平衡因子
//subLR的左子树会被放到curNode的右孩子位置,而subRL的右子树会被放到parent的左孩子位置
if (bf == -1)
{
parent->_bf = 1;
curNode->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = 0;
curNode->_bf = -1;
}
}
//平衡因子调整结束退出循环
break;
}
}
return true;
}
//节点的删除
bool Erase(const T& val)
{
//1.查找节点
Node* parent = nullptr;
Node* curNode = _root;
while (curNode)
{
if (val == curNode->_val)
{
break;
}
else if (val < curNode->_val)
{
parent = curNode;
curNode = curNode->_left;
}
else
{
parent = curNode;
curNode = curNode->_right;
}
}
//节点不存在
if (!curNode)
{
return false;
}
//2.删除节点
if (!curNode->_left && !curNode->_right)
{
//左右子树都为空,直接删除节点,更新父节点的平衡因子
if (curNode == parent->_left)
{
//删除的是父节点的左孩子,父节点平衡因子+1
++parent->_bf;
parent->_left = nullptr;
}
else
{
//删除的是父节点的右孩子,父节点平衡因子-1
--parent->_bf;
parent->_right = nullptr;
}
//删除待删除节点
delete curNode;
//将当前节点更新为父节点,为下一步平衡因子的调整做准备
curNode = parent;
}
else if (!curNode->_right)
{
//右子树为空
//删除的节点只有左孩子,将要删除节点的值替换为左孩子的值,删除左孩子
Node* leftNode = curNode->_left;
curNode->_val = leftNode->_val;
//删除节点
curNode->_left = nullptr;
delete leftNode;
leftNode = nullptr;
++curNode->_bf; //删除了左孩子,当前节点平衡因子+1
}
else if (!curNode->_left)
{
//左子树为空
//删除的节点只有右孩子,将要删除节点的值替换为右孩子的值,删除右孩子
Node* rightNode = curNode->_right;
curNode->_val = rightNode->_val;
//删除节点
curNode->_right = nullptr;
delete rightNode;
rightNode = nullptr;
--curNode->_bf; //删除了右孩子,当前节点的平衡因子-1
}
else
{
//左右子树都存在
//将要删除节点的值替换为前驱节点的值(左孩子的最右节点),删除前驱节点
Node* prev = curNode->_left; //前驱节点
parent = curNode; //更新父节点
//找到左子树的最右节点
while (prev->_right)
{
parent = prev;
prev = prev->_right;
}
curNode->_val = prev->_val; //进行值替换
//更新父节点指向和父节点的平衡因子
if (parent->_left == prev)
{
parent->_left = prev->_left;
++parent->_bf;
}
else
{
parent->_right = prev->_left;
--parent->_bf;
}
//删除节点
delete prev;
prev = nullptr;
//将当前节点更新为父节点,便于后续进行平衡因子的调整
curNode = parent;
}
//3.调整平衡因子,此处的调整和插入节点相同
parent = curNode->_parent; //更新父节点
//当前节点的左右孩子不平衡,更新调整起始位置
if (curNode->_bf == 2 || curNode->_bf == -2)
{
//左边高,将调整位置更新为左孩子
if (curNode->_bf == -2)
{
Node* subL = curNode->_left; //左孩子
parent = curNode;
curNode = subL;
}
//右边高,将调整位置更新为右孩子
else
{
Node* subR = curNode->_right;
parent = curNode;
curNode = subR;
}
}
//向上进行平衡因子的调整,直到根节点
while (parent)
{
//重新计算父节点的平衡因子,此时的平衡因子不能只根据左右孩子进行判断,需要根据高度进行计算
parent->_bf = calNodeBf(parent);
//删除节点之后打破了AVL树的结构,需要进行旋转
if (abs(parent->_bf) == 2)
{
if (parent->_bf == 2 && curNode->_bf == 1)
{
//右边的右边高,进行左单旋
RotateL(parent);
}
else if (parent->_bf == 2 && curNode->_bf == -1)
{
Node* subRL = curNode->_left; //当前节点的左孩子
int bf = subRL->_bf;
//右边的左边高,先右旋再左旋
RotateR(curNode);
RotateL(parent);
//进行平衡因子的修正
//subRL左右子树高度的不一致会影响parent和curNode的平衡因子
//subRL的右子树会被放到curNode的左孩子位置,而subRL的左孩子会被放到parent的右孩子位置
if (bf == 1)
{
parent->_bf = -1;
curNode->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 0;
curNode->_bf = 1;
}
}
else if (parent->_bf == -2 && curNode->_bf == -1)
{
//左边的左边高,右旋
RotateR(parent);
}
else if (parent->_bf == -2 && curNode->_bf == 1)
{
Node* subLR = curNode->_right;
int bf = subLR->_bf;
//左边的右边高,先左旋再右旋
RotateL(curNode);
RotateR(parent);
//进行平衡因子的修正
//subLR左右子树高度的不一致会影响parent和curNode的平衡因子
//subLR的左子树会被放到curNode的右孩子位置,而subRL的右子树会被放到parent的左孩子位置
if (bf == -1)
{
parent->_bf = 1;
curNode->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = 0;
curNode->_bf = -1;
}
}
}
//以parent为根节点的树没有打破平衡,但是上层可能被打破平衡,需要向上调整
curNode = parent;
parent = curNode->_parent;
}
return true;
}
//判断一颗树是不是AVL树
bool IsAVLTree()
{
//AVL树需要满足平衡和中序有序两个性质
return IsBalanced(_root) && IsOrdered();
}
private:
//递归销毁AVL树
void Destroy(Node* root)
{
if (!root)
{
return;
}
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}
//进行左单旋
void RotateL(Node* parent)
{
if (!parent)
{
return;
}
Node* subR = parent->_right; //右子树的根节点,一定存在
Node* subRL = subR->_left; //右子树的左孩子的根节点,可能存在
Node* pparent = parent->_parent; //当前树的根节点的父节点,可能存在
subR->_left = parent;
parent->_parent = subR;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
subR->_parent = pparent;
if (!pparent)
{
//当前节点是根节点,更新根节点
_root = subR;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = subR;
}
else
{
pparent->_right = subR;
}
}
parent->_bf = 0;
subR->_bf = 0;
}
//进行右单旋
void RotateR(Node* parent)
{
if (!parent)
{
return;
}
Node* subL = parent->_left; //根节点的左孩子,一定存在
Node* subLR = subL->_right; //左孩子的右孩子,可能存在
Node* pparent = parent->_parent; //根节点的父节点,可能存在
subL->_right = parent;
parent->_parent = subL;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
subL->_parent = pparent;
if (!pparent)
{
_root = subL;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = subL;
}
else
{
pparent->_right = subL;
}
}
parent->_bf = 0;
subL->_bf = 0;
}
//获取节点的高度
int getHeight(Node* node)
{
int h = 0;
queue<Node*> q;
if (node)
{
q.push(node);
}
while (!q.empty())
{
int sz = q.size();
while (sz--)
{
Node* front = q.front();
q.pop();
if (front->_left)
{
q.push(front->_left);
}
if (front->_right)
{
q.push(front->_right);
}
}
++h;
}
return h;
}
//计算节点平衡因子
int calNodeBf(Node* node)
{
if (!node)
{
return 0;
}
int l = getHeight(node->_left);
int r = getHeight(node->_right);
return r - l;
}
//中序遍历是否有序
bool IsOrdered()
{
stack<Node*> st;
Node* curNode = _root;
Node* prev = nullptr; //前一个访问的节点,前驱节点
while (curNode || !st.empty())
{
while (curNode)
{
st.push(curNode);
curNode = curNode->_left;
}
Node* top = st.top();
//如果前驱节点的值大于等于当前节点的值,不满足AVL树的性质
if (prev && prev->_val >= top->_val)
{
return false;
}
//更新前驱节点
prev = top;
st.pop();
cout << top->_val << "\tbf: " << top->_bf << endl;
curNode = top->_right;
}
return true;
}
//判断是否平衡
bool IsBalanced(Node* root)
{
if (!root)
{
return true;
}
int lh = getHeight(root->_left);
int rh = getHeight(root->_right);
return abs(lh - rh) <= 1
&& IsBalanced(root->_left)
&& IsBalanced(root->_right);
}
};
测试代码
#include <iostream>
#include <time.h>
#include "AVLTree.h"
using namespace std;
void test01()
{
AVLTree<int> tree;
int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7,16, 14 };
int len = sizeof(arr) / sizeof(arr[0]);
for (int i = 0; i < len; ++i)
{
tree.Insert(arr[i]);
}
bool ret = tree.IsAVLTree();
if (ret)
{
cout << "这是一颗AVL树" << endl;
}
else
{
cout << "这不是一棵AVL树" << endl;
}
}
void test02()
{
AVLTree<int> tree;
int arr2[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
int len = sizeof(arr2) / sizeof(arr2[0]);
for (int i = 0; i < len; ++i)
{
tree.Insert(arr2[i]);
}
bool ret = tree.IsAVLTree();
if (ret)
{
cout << "这是一颗AVL树" << endl;
}
else
{
cout << "这不是一棵AVL树" << endl;
}
}
void test_remove()
{
int arr[] = { 6, 3, 2, 1, 4, 5, 8, 7, 10, 9, 11 };
int len = sizeof(arr) / sizeof(arr[0]);
AVLTree<int> t;
for (int i = 0; i < len; ++i)
{
t.Insert(arr[i]);
}
bool ret = t.IsAVLTree();
if (ret)
{
cout << "这是一颗AVL树" << endl;
}
else
{
cout << "这不是一棵AVL树" << endl;
}
/*
//1.被删除节点不存在左右孩子
t.Erase(8);
ret = t.IsAVLTree();
if (ret)
{
cout << "这是一颗AVL树" << endl;
}
else
{
cout << "这不是一棵AVL树" << endl;
}
*/
/*
//2.被删除节点只有左孩子
t.Erase(2);
ret = t.IsAVLTree();
if (ret)
{
cout << "这是一颗AVL树" << endl;
}
else
{
cout << "这不是一棵AVL树" << endl;
}
*/
/*
//3.被删除节点只有右孩子
t.Erase(10);
ret = t.IsAVLTree();
if (ret)
{
cout << "这是一颗AVL树" << endl;
}
else
{
cout << "这不是一棵AVL树" << endl;
}
*/
/*
//4.1:被删除节点有左右孩子,而且是根节点
t.Erase(7);
ret = t.IsAVLTree();
if (ret)
{
cout << "这是一颗AVL树" << endl;
}
else
{
cout << "这不是一棵AVL树" << endl;
}
*/
//4.2:被删除节点有左右孩子,但不是根节点
//t.Erase(3);
t.Erase(9);
ret = t.IsAVLTree();
if (ret)
{
cout << "这是一颗AVL树" << endl;
}
else
{
cout << "这不是一棵AVL树" << endl;
}
}
void test_total()
{
srand(time(NULL));
AVLTree<int> t;
cout << "请输入树节点个数: ";
int n;
cin >> n;
cout << "树节点范围为0~10000,现在开始插入节点";
for (int i = 0; i < n; ++i)
{
t.Insert(rand() % 10000);
}
bool ret = t.IsAVLTree();
if (!ret)
{
cout << "这不是AVL树" << endl;
}
else
{
cout << "这是一颗AVL树" << endl;
}
}
int main()
{
//test01();
//test02();
test_remove();
//test_total();
return 0;
}