• 广度优先遍历（BFS）
• 深度优先遍历（DFS）

图的广度优先遍历

广度优先遍历：通过某一个结点，找到与之相邻的结点。

与树的广度优先遍历（层序遍历）联系：

树就是找孩子，图可以用之前提到的两个基本操作（FirstNeighbor和NextNeighbor）实现。

因为树不存在“回路”，所以树在搜索相邻的结点时，不可能搜到已经访问过的结点。但是图有可能出现环路，所以图在搜索相邻结点时，有可能搜到已经访问过的顶点。图需要一个标记，来记录已经访问过的顶点。

树在进行广度优先遍历（层序遍历）时，借助了一个辅助队列来实现：

1、若树非空，则根结点入队；

2、若队列非空，队头元素出队并访问，同时将该元素的孩子依次入队；

3、重复②直到队列为空。

图的广度优先遍历，也需要一个辅助队列：

1、找到与一个顶点相邻的所有顶点（两个基本操作）；

FirstNeighbor(G,x)：求图G中顶点x的第一个邻接点，若有则返回顶点序号。若x没有邻接点或图中不存在x，则返回-1。

NextNeighbor(G,x,y)：假设图G中顶点y是顶点x的一个邻接点，返回除y之外顶点x的下一个邻接点的顶点序号，若y是x的最后一个邻接点，则返回-1。

2、标记哪些顶点被访问过；

设置bool型数组visited[ ]记录访问过的数组。bool visited[MAX_VERTEX_NUM];

3、需要一个辅助队列。

【注意】：使用邻接矩阵存储的图的遍历，和使用邻接表存储的图的遍历，在第一步的实现有些区别。

代码实现如下：

bool visited[MAX_VERTEX_NUM];    //标记访问数组，初始值全部设为false

//广度优先遍历
void BFS(Graph G,int v){         //从顶点v出发，广度优先遍历图G
    visit(v);                //访问初始顶点v
    visited[v]=TRUE;         //对v做已访问标记
    Enqueue(Q,v);            //顶点v入队列Q
    while(!isEmpty(Q)){
        DeQueue(Q,v);        //顶点v出队列
        for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
            //检测v的所有邻接点
            if(!visited[w]){        //w为v的尚未访问的邻接顶点
                visit(w);           //访问顶点w
                visited[w]=TRUE;    //对w做已访问标记
                EnQueue(Q,w);       //顶点w入队列
            }//if
    }//while
}

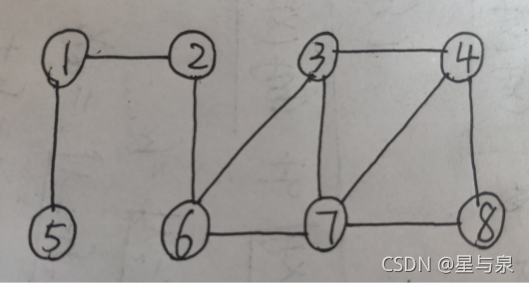
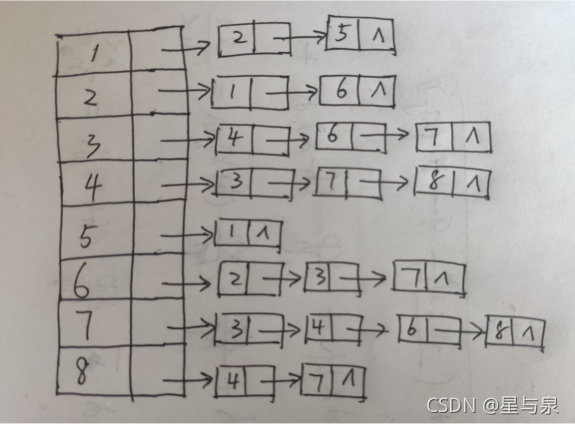
例子：用广度优先算法遍历下图。

  一开始，visited[ ]数组的值全部为false，表示没有任何顶点被访问。