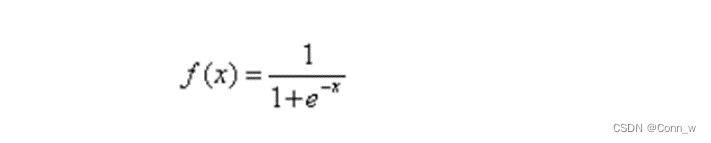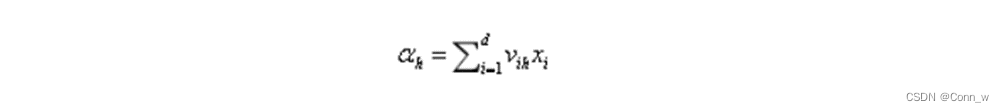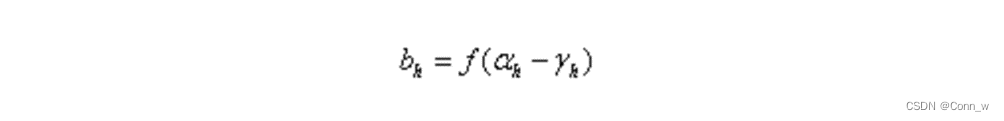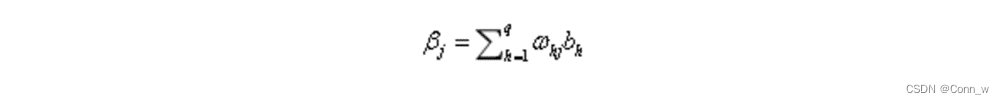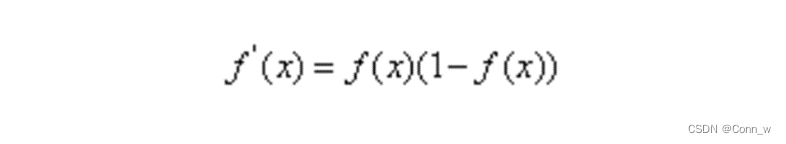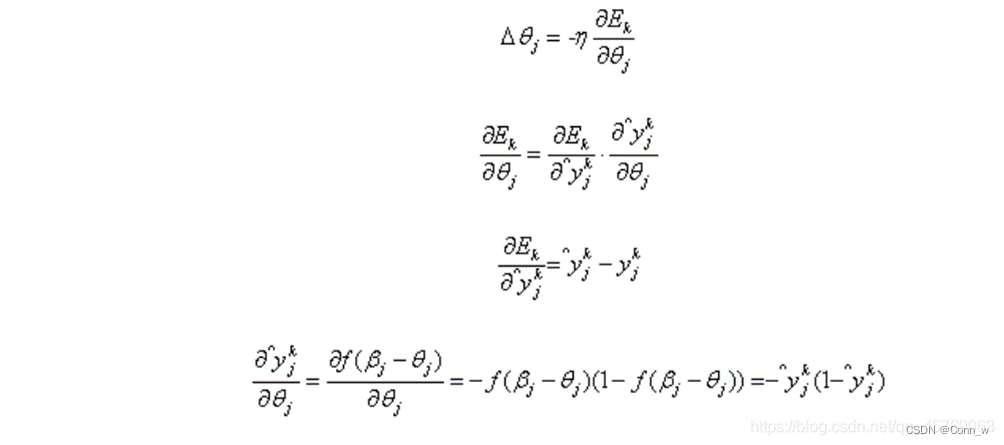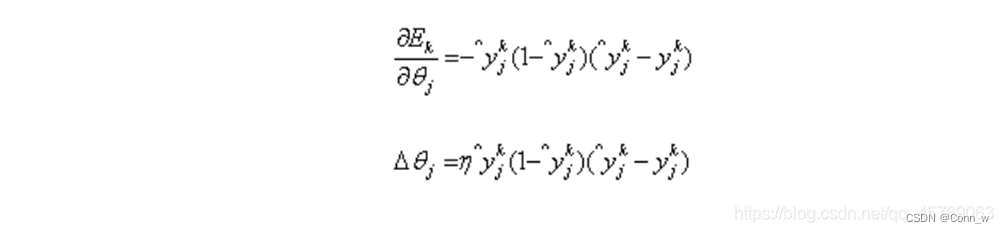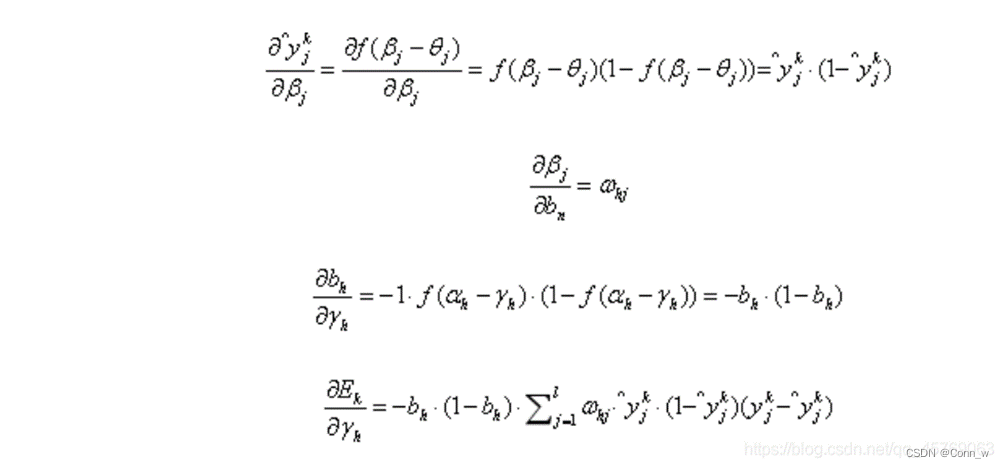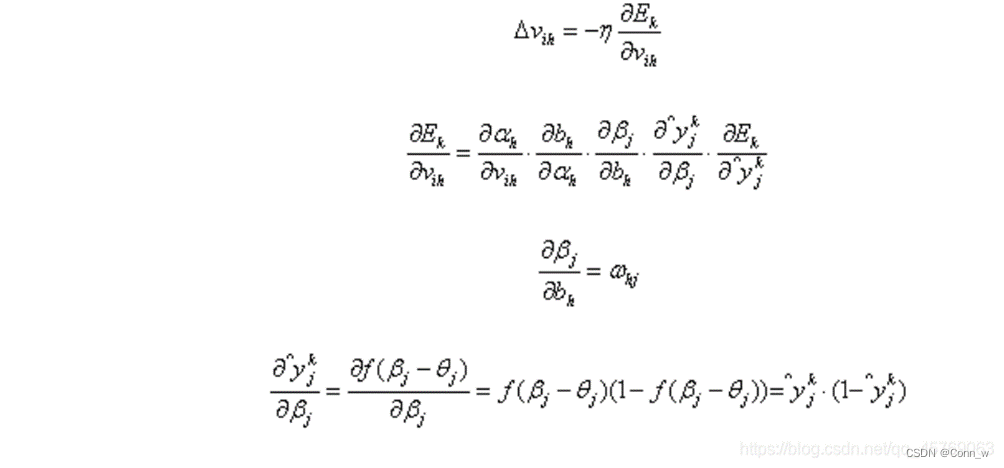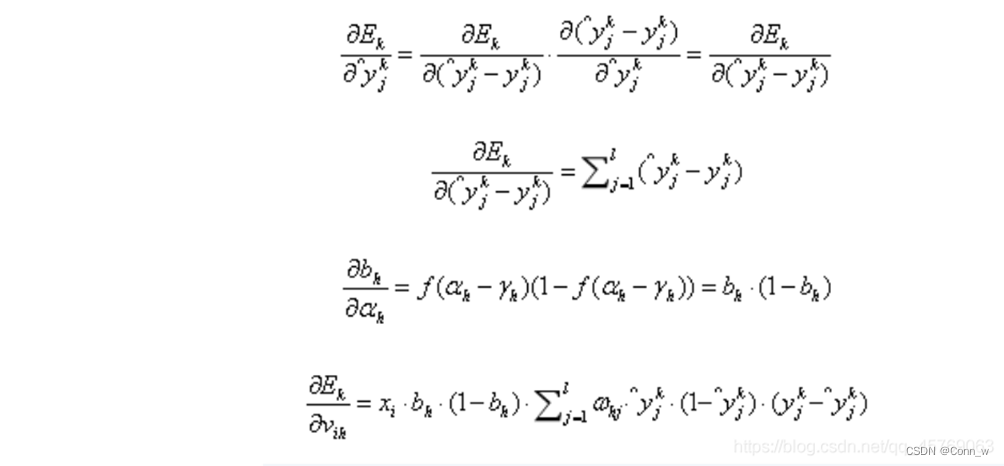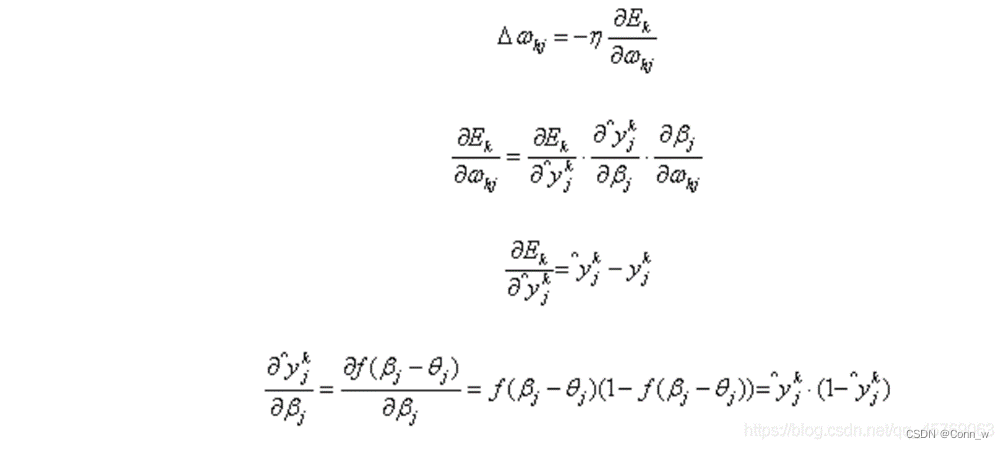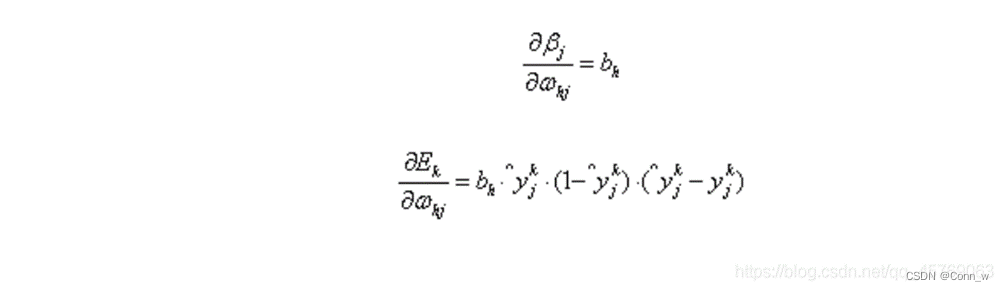基于 BP 神经网络的分类实验

一、实验目的

掌握 BP 神经网络的结构和运行机制，设计实现 BP 神经网络实现分类任务。

二、实验思路

1、数据准备（通过读取数据文件获取）
2、数据处理（读取的数据是字符串形式，需要将其转换为浮点数或者整型）
3、数据划分（将特征和标签分割开）
4、初始化待估参数（通过自定义超参数每层神经元的个数来进行初始化待估参数）——这里不需要定义层数，因为这里只有一个隐层
5、参数迭代更新（用初始化的待估参数去对样本数据进行逐一训练，并且不断地迭代更新，最后得到最优的待估参数）——这里和上一步其实就基本上将整个神经网络的框架已经搭建好了
6、测试模型（利用上面得到的参数，对测试样本集进行测试，查看准确率）

三、实验记录

一、BP 神经网络结构和原理
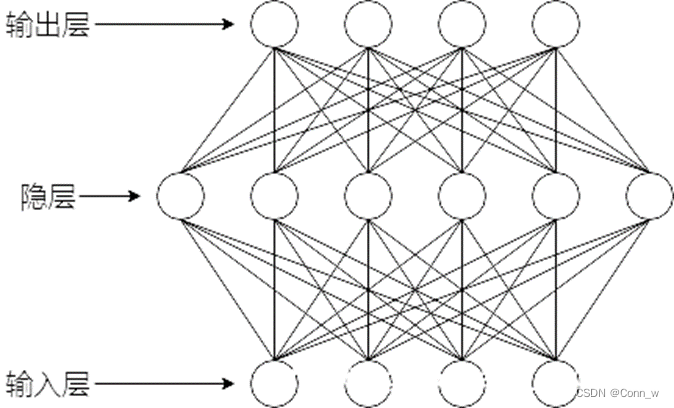
BP 神经网络是一种前向反馈神经网络，由输入层、隐藏层和输出层组成。它通过 反向传播算法来训练多层神经网络， 即将误差从输出层反向传播到输入层， 利用链
式法则对每个神经元的权值进行调整，从而使网络输出的误差最小。 二、 BP 神经网络的具体流程如下：
初始化网络权值，包括输入层与隐藏层的权重和偏置，以及隐藏层与输出层的权重和偏置。
输入样本数据，将数据经过前向传播的过程，得到输出结果。
计算输出误差， 根据误差公式来计算输出误差值，根据这一误差值来对下一次权值 调整进行判断是否已达到目标误差范围。
反向传播误差，依次计算每一层上的误差项，并将误差项反向传递到前一层。 根据误差项计算梯度，计算每个权重和偏执对误差的贡献。
更新权值和偏执，根据梯度和学习率来更新每个权重和偏执的值。上述过程，直到达到预设的误差允许范围或达到迭代次数限制。
BP神经网络分类的损失函数通常选择交叉熵损失函数，它可以测量实际输出和期望输出之间的差异。交叉熵损失函数的代价更符合实际情况，因为它适用于两个概率分布之间的距离度量。
神经网络模型
一个神经元即一个感知机模型，由多个神经元相互连接形成的网络，即神经网络。

神经网络数学模型定义
对于该模型有如下定义：
训练集：D={(x1, y1), (x2, y2), …, (xm, ym)}，x具有d个属性值，y具有k个可能取值
则我们的神经网络（单隐层前馈神经网络）应该是具有d个输入神经元，q个隐层神经元，k个输出层神经元的神经网络 ，我们默认输入层只是数据的输入，不对数据做处理，即输入层没有阈值。
1）激活函数

2）各层权重、阈值定义
输出层第j个神经元的阈值为：θj
隐层第h个神经元的阈值为：γh（γ是Gamma）
输入层第i个神经元与隐层第h个神经元的连接权重为：vih
隐层第h个神经元与输出层第j个神经元的连接权重为：ωhj
3）各层输入输出定义
输入层的输入和输出一样，就是样本数据
隐层第h个神经元的输入

隐层第h个神经元的输出

输出层第j个神经元的输入

输出层的输出跟隐层的输出类似
4、优化问题的目标函数与迭代公式
1）目标函数
对参数进行估计，需要有优化方向，我们继续使用欧式距离，或者均方误差来作为优化目标：

2）待估参数的优化迭代公式
我们使用梯度下降的策略对参数进行迭代优化，所以任意一个参数的变化大小为（θ代表任意参数）：

下面根据这个更新公式，我们来求各个参数的更新公式：
对数几率函数的导数如下：

输出层第j个神经元的阈值θj：


隐层第h个神经元的阈值γh：

输入层第i个神经元与隐层第h个神经元的连接权重vih ：


隐层第h个神经元与输出层第j个神经元的连接权重ωhj：


现在四个参数的更新规则都计算出来了。

四、实验结果

在本次实验中，从网上下载 MNIST 数据集，将选择图像转换成灰度图像，并使用 Python 编写 BP 神经网络分类程序。
实验参数如下：
输入层节点数： 784
隐藏层节点数： 100
输出层节点数： 10
学习率： 0.1
迭代次数： 1000
经过训练， BP 神经网络的准确率为 0.974，表明 BP 神经网络可用于图像分类。

五、实验分析

通过实验可知， BP 神经网络分类方法是有效的，并能够得到较高的分类准确率。 但是， 在设计该算法时， 还需进行合理的参数选择， 主要包括隐藏层节点数、学习 率等参数的选取。同时， 在训练过程中， 也需要注意训练集、验证集和测试集等数 据的划分，以充分验证模型的泛化性能。