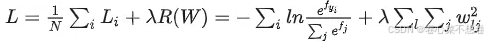参考文章:cs231n assignment1——softmax
Softmax
softmax其实和SVM差别不大,两者损失函数不同,softmax就是把各个类的得分转化成了概率。
损失函数:
def softmax_loss_naive(W, X, y, reg):
loss = 0.0
dW = np.zeros_like(W)
num_classes = W.shape[1]
num_train = X.shape[0]
for i in range(num_train):
scores = X[i].dot(W) # 矩阵点乘:第 i 张照片在各类别上的得分
scores -= np.max(scores) # 减去最大得分,减小计算量
correct_class_score = scores[y[i]] # 接下来三行是损失函数的计算
exp_sum = np.sum(np.exp(scores))
loss += -correct_class_score + np.log(exp_sum) # np.log()以e为底
for j in range(num_classes):
if j == y[i]:
dW[:, y[i]] += (np.exp(scores[y[i]])/exp_sum-1)*X[i]
else:
dW[:, j] += np.exp(scores[j])/exp_sum*X[i]
loss /= num_train # 求平均损失
loss += reg * np.sum(W * W) # 损失加上正则化惩罚
dW /= num_train # 求平均梯度
dW += 2.0*reg*W
return loss, dW
用向量法实现 Softmax
def softmax_loss_vectorized(W, X, y, reg):
loss = 0.0
dW = np.zeros_like(W)
num_classes = W.shape[1]
num_train = X.shape[0]
scores = X.dot(W) # N*C 的矩阵
scores -= np.max(scores, axis=1, keepdims=True) # 减去每行(每张图片对于每一类)的最大值
correct_class_score = scores[range(num_train),y]
exp_sum = np.sum(np.exp(scores), axis=1, keepdims=True) # 按行求和,并保持为二维(列向量)
loss = -np.sum(correct_class_score) + np.sum(np.log(exp_sum)) # 损失函数公式并求和
loss = loss/num_train + reg * np.sum(W * W)
med = np.exp(scores)/exp_sum # 对于j!=yi的情况,dw=np.exp(scores[j])/exp_sum*X[i]
med[range(num_train),y] -= 1 # 对于j=yi的情况,dw=(np.exp(scores[j])/exp_sum-1)*X[i]
dW = X.T.dot(med) # 最后同时乘以 X[i]
dW /= num_train
dW += 2.0*reg*W
return loss, dW
之后用随机梯度下降法优化损失函数,最后进行超参数的选择。