【笔记】奇异值分解&特征值分解通俗易懂

特征值分解

公式解析

矩阵乘法本质上是一种变换，是把一个向量，通过旋转，拉伸变成另一个向量的过程。
公式：
$Av=\lambda v \tag{1}$
描述的就是矩阵 $A$ 对向量 $v$ 的变换只有拉伸，没有旋转。
也可以看成矩阵 $A$ ，向量 $v$ ，系数 $\lambda$ ，这三者建立了一种联系，但显然无法通过式（1）来用 $v$ 和 $\lambda$ 表示 $A$ ，因此这个式子是不完备的，对于一个秩为 $m$ 的矩阵A，应该存在 $m$ 个这样的式子，完备的式子应该是：
$A\left(\vec{v}_{1}, \vec{v}_{2}, \ldots, \vec{v}_{m}\right)= \left(\lambda_{1} \vec{v}_{1}, \lambda_{2} \vec{v}_{2}, \ldots, \lambda_{m} \vec{v}_{m}\right)= \left(\vec{v}_{1}, \vec{v}_{2}, \ldots, \vec{v}_{m}\right)\left[\begin{array}{ccc}{\lambda_{1}} & {\cdots} & {0} \\ {\vdots} & {\ddots} & {\vdots} \\ {0} & {\cdots} & {\lambda_{m}}\end{array}\right] \tag{2}$
写成矩阵的形式为：
$V=V\Lambda \tag{3}$
通过式(3)，将A表示为：
$\Lambda V^{-1} \tag{4}$
这种形式就可以看成矩阵 $A$ 被分解了。
一般我们会把V矩阵的m个特征向量标准化，即满足 $v_i||_2=1$ ,或者 $v_i^Tv_i=1$ ,此时V的m个特征向量为标准正交基，满足 $V^TV=I,即V^T=V^{-1}$ ,也就是说V为酉矩阵。因此特征分解的表达式也可以写成：
$\Lambda V^{T} \tag{5}$

为什么要这样做？

特征值和特征向量是为了研究向量在经过线性变换后的方向不变性提出的。
一个矩阵和该矩阵的非特征向量相乘是对该向量的旋转变换，和其特征向量相乘是对该向量的伸缩变换，其中伸缩的程度取决于特征值的大小。
矩阵在特征向量所指的方向上具有增强（或减弱）特征向量的作业，也就是说，如果矩阵持续迭代作用于向量，那么特征向量就会突显出来。

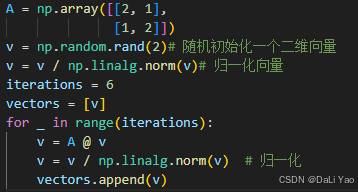
例子

初始化一个矩阵 $\begin{bmatrix} 2&1\\ 1&2\\ \end{bmatrix}$
计算出其特征值为 $[3.0 1.0]$ ，特征向量为：
$\begin{bmatrix} 0.70710678&-0.70710678\\ 0.70710678&0.70710678\\ \end{bmatrix}$
最大值对应的特征向量为 $u = [0.70710678 0.70710678]$

随机一个向量 $v$ （下图以 $v = [01]$ 为例），经过多次矩阵乘法运算后 $A^6v=[0.70613615 ~~~0.70807608]$ ,不断靠近最大特征值对应的特征向量 $u$ 。
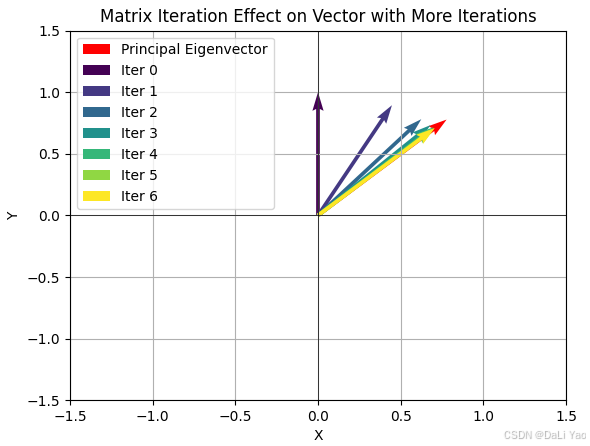
在这里插入图片描述
画出 $v, Av,A^2v,A^3v,A^4v,A^5v,A^6v,u,A^6v和u$ 几乎重合，增大矩阵乘法到100次数后 $A^{100}v=u$ (这里为了方便观察，手动将特征向量拉长了10%)

不断左乘A后，变换后的归一化向量会恒等于 $u$ ，这佐证了矩阵是具有某种不变的特性的。为了提取矩阵这种“不变性”，或者说是为了描述变换（矩阵乘法是一种线性变换）的主要方向是非常有必要的。

特征值计算

$Av=\lambda v\to Av=\lambda Iv\to (\lambda I-A)v=0$
根据线性方程组理论，为了使这个方程有非零解，矩阵 $(\lambda I-A)$ 的行列式必须是零，即：
$det(\lambda I-A)=0$
上式也被称为 $A$ 的特征方程，计算出所有的 $\lambda$ 后，再代入 $(\lambda I-A)v=0$ 求解出对应的 $v$ 。

应用

图像压缩

在图像压缩里，一张图片就可以看作是一个矩阵，当我们提取了这个矩阵的特征值和特征向量后，我们可以只用最大的几个特征值（其他的变为0）就可以基本复原这张图片。

奇异值分解(SVD)

定义

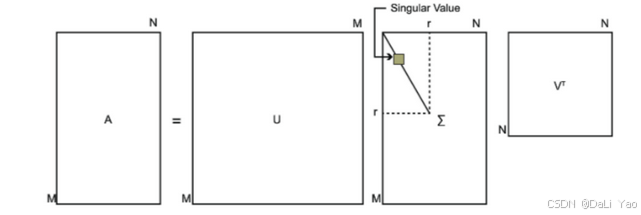
SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵 $A$ 是一个 $m \times n$ 的矩阵，那么我们定义矩阵 $A$ 的SVD为：
$A=U\Sigma V^T\tag{6}$
其中U是一个m×m的矩阵，\Sigma是一个m×n的矩阵，除了主对角线上的元素以外全是0，主对角线上的元素称为奇异值，V是一个n×n的矩阵。U和V都是酉矩阵，即： $U^TU=I,V^TV=I$ ，下图可以形象看出SVD的定义：
在这里插入图片描述

计算U, $\Sigma$ , V

将 $A$ 的转置和 $A$ 做矩阵乘法，那么会得到 $n \times n$ 的一个方阵 $A^TA$ 。既然 $A^TA$ 是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式:
$(A^TA)v_i=\lambda_iv_i$
这样就可以得到 $A^TA$ 的特征向量矩阵V，一般将V中的每个特征向量叫做A的右奇异向量。
将A和A的转置做矩阵乘法，那么会得到m×m的一个方阵 $AA^T$ 。既然 $AA^T$ 是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：
$(AA^T)u_i=\lambda_iu_i$
这样就可以得到 $AA^T$ 的特征向量矩阵U，一般将U中的每个特征向量叫做A的右奇异向量。
$\Sigma$ 除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值 $\sigma$ 就可以了。
注意到：
$A=U\Sigma V^T \Rightarrow AV=U\Sigma V^TV \Rightarrow AV=U\Sigma\Rightarrow Av_i=\sigma _iu_i \Rightarrow \sigma _i=\frac{Av_i}{u_i}\tag{7}$
这样就可以得到奇异值矩阵 $\Sigma$ 。
$A^TA$ 的特征向量组成的就是我们SVD中的V矩阵，而 $AA^T$ 的特征向量组成的就是我们SVD中的U矩阵，这有什么根据吗？证明如下：（以 $V$ 矩阵为例）
$A=U\Sigma V^T \Rightarrow A^T=V\Sigma ^T U^T \Rightarrow A^TA=V\Sigma UU^T\Sigma ^TV^T=V\Sigma ^2 V^T\tag{8}$
这就和特征分解中的式（5）对应上了。U矩阵同理可证。
可以看出特征值矩阵等于奇异值矩阵的平方，特征值和奇异值满足如下关系：
$\sigma _i = \sqrt{\lambda_i}\tag{9}$
所以可以通过（7）式和（9）式计算奇异值。

应用

奇异值,跟特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。
因此可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵：
$A_{m×n}=U_{m×m}\Sigma _{m×n}V_{n×n}^T \thickapprox U_{m×k}\Sigma _{k×k}V_{k×n}^T$
其中 $k$ 比 $m$ 小得多

PCA降维

主成分分析 (PCA, Principal Component Analysis) 是一种常用于数据降维的线性技术。它通过寻找数据中的主要方向（主成分），在保持数据方差（信息量）最大化的前提下，压缩数据的维度。PCA 降维的主要思想是将高维数据投影到低维空间，同时尽量保留数据的原始结构和特征。下面我们详细解释 PCA 的原理。

PCA 的主要步骤

在这里插入图片描述

参考链接：

https://zhuanlan.zhihu.com/p/314464267
https://zhuanlan.zhihu.com/p/29846048