MATLAB实现遗传算法在扫地机器人路径规划中的应用
1、项目下载:
本项目完整讲解和全套实现源码见下资源,有需要的朋友可以点击进行下载
| 说明 | 文档(点击下载) |
|---|---|
| 全套源码+学术论文 | 扫地机器人路径规划中遗传算法的应用与MATLAB实现-遗传算法-路径规划-扫地机器人-优化搜索-matlab |
更多阿里matlab精品数学建模项目可点击下方文字链接直达查看:
300个matlab精品数学建模项目合集(算法+源码+论文)
2、项目介绍:
遗传算法在扫地机器人路径规划中的应用与实现
摘要
随着智能家居技术的快速发展,扫地机器人作为一种重要的家庭服务机器人,其路径规划能力直接影响其清洁效率和用户体验。遗传算法(Genetic Algorithm,简称GA)作为一种基于自然选择和遗传机制的优化搜索算法,在解决复杂路径规划问题上表现出色。本文详细探讨了遗传算法在扫地机器人路径规划中的应用,包括问题定义、编码表示、初始化种群、适应度函数设计、选择操作、交叉操作、变异操作、迭代过程以及最佳解提取等关键环节。同时,本文还提供了相应的MATLAB源代码,并通过运行实例展示了算法的有效性。
关键词
遗传算法;扫地机器人;路径规划;优化搜索;MATLAB
一、引言
1.1研究背景与意义
随着生活水平的提高,智能家居产品逐渐普及,扫地机器人作为其中的代表,为人们的日常生活带来了极大的便利。然而,扫地机器人的路径规划问题一直是制约其清洁效率和智能化水平的关键因素之一。传统的路径规划方法如栅格法、可视图法等虽然能够在一定程度上解决问题,但在面对复杂环境和动态障碍物时,往往难以取得令人满意的效果。因此,研究一种更加高效、智能的路径规划算法具有重要意义。
遗传算法作为一种基于自然选择和遗传机制的优化搜索算法,通过模拟生物进化过程中的选择、交叉和变异等操作,能够在复杂的搜索空间中寻找到全局最优解或近似最优解。将遗传算法应用于扫地机器人的路径规划中,有望提高其清洁效率和智能化水平,为智能家居技术的发展贡献力量。
1.2研究现状
目前,遗传算法在机器人路径规划领域已经得到了广泛的应用和研究。国内外学者提出了多种基于遗传算法的路径规划方法,如二进制编码方法、实数编码方法、混合编码方法等。这些方法在解决不同场景下的路径规划问题时表现出色,但也存在一些不足之处,如计算量大、收敛速度慢等。因此,如何进一步提高遗传算法在路径规划中的效率和性能,成为当前研究的热点之一。
1.3研究内容
本文旨在探讨遗传算法在扫地机器人路径规划中的应用与实现。具体研究内容包括:
- 问题定义:将扫地任务看作是一个优化问题,目标是找到从起点到终点的最短或最优路径,同时考虑避免障碍物。
- 编码表示:采用二进制串或矩阵等数据结构来代表可能的路径,每个基因位代表一步的方向。
- 初始化种群:生成一组随机的初始路径解作为“个体”,即种群。
- 适应度函数:设计基于路径长度和碰撞次数的适应度函数,用于评估每个个体的优劣。
- 选择操作:按照一定的概率选择优秀的个体进入下一轮,劣质个体被淘汰。
- 交叉操作:模拟生物繁殖过程,通过配对两个父母个体并交换部分基因来创建新的个体。
- 变异操作:引入随机变化,增加种群多样性,防止陷入局部最优解。
- 迭代过程:重复上述步骤多代,直到达到预设的最大迭代次数或适应度满足阈值。
- 最佳解提取:从最终种群中提取最优的个体作为扫地机器人的路径规划结果。
二、遗传算法在扫地机器人路径规划中的应用
2.1问题定义
在扫地机器人的路径规划中,我们首先将扫地任务看作是一个优化问题。目标是找到从起点到终点的最短或最优路径,同时考虑避免障碍物。路径规划过程中需要考虑的因素包括路径长度、碰撞次数、转弯次数等。其中,路径长度是最主要的优化目标,因为它直接关系到扫地机器人的清洁效率。同时,为了避免与障碍物发生碰撞,我们还需要在路径规划过程中考虑碰撞次数这一因素。
2.2编码表示
在遗传算法中,编码表示是将问题的解空间映射到遗传算法能够处理的搜索空间的关键步骤。对于扫地机器人的路径规划问题,我们可以采用二进制串或矩阵等数据结构来代表可能的路径。其中,二进制串编码是一种简单且常用的编码方法。在这种编码方法中,每个基因位代表一步的方向,如0表示向前、1表示向左等。通过组合不同的基因位,我们可以得到一条完整的路径。
除了二进制串编码外,我们还可以采用矩阵编码方法来表示路径。在这种编码方法中,矩阵的每个元素代表一个栅格或节点,元素的值表示从该栅格或节点出发可以到达的下一个栅格或节点的方向。通过遍历矩阵并按照指定的方向移动,我们可以得到一条完整的路径。
2.3初始化种群
初始化种群是遗传算法的第一步,其目的是生成一组随机的初始路径解作为“个体”,即种群。在扫地机器人的路径规划问题中,我们可以通过随机生成一组二进制串或矩阵来初始化种群。每个个体代表一条可能的路径,其优劣程度将通过后续的适应度评估来确定。
2.4适应度函数
适应度函数是遗传算法中用于评估每个个体优劣程度的指标。在扫地机器人的路径规划问题中,我们可以设计基于路径长度和碰撞次数的适应度函数。具体来说,适应度函数可以表示为路径长度的倒数减去碰撞次数的加权和。这样,路径越短且碰撞次数越少的个体将获得更高的适应度值,从而更有可能被选择进入下一轮迭代。
2.5选择操作
选择操作是遗传算法中的关键环节之一,其目的是按照一定的概率选择优秀的个体进入下一轮迭代,劣质个体则被淘汰。在扫地机器人的路径规划问题中,我们可以采用轮盘赌选择法、锦标赛选择法等多种选择方法。其中,轮盘赌选择法是一种简单且常用的选择方法。在这种方法中,每个个体的选择概率与其适应度值成正比。通过随机生成一个介于0和1之间的数,并将其与个体的累积适应度值进行比较,我们可以确定哪个个体被选中进入下一轮迭代。
2.6交叉操作
交叉操作是遗传算法中模拟生物繁殖过程的关键步骤之一。在扫地机器人的路径规划问题中,我们可以通过配对两个父母个体并交换部分基因来创建新的个体。具体来说,我们可以采用单点交叉、双点交叉等多种交叉方法。以单点交叉为例,我们首先随机选择一个交叉点,然后将两个父母个体在交叉点前后的基因进行交换,从而得到两个新的子代个体。
2.7变异操作
变异操作是遗传算法中引入随机变化以增加种群多样性的关键步骤之一。在扫地机器人的路径规划问题中,我们可以通过随机改变某些基因位的值来引入变异。具体来说,我们可以设置一个变异概率,然后对每个个体的每个基因位进行随机判断。如果满足变异条件,则将该基因位的值进行取反操作(如0变为1,1变为0)。通过引入变异操作,我们可以有效地防止遗传算法陷入局部最优解,并提高算法的搜索效率。
2.8迭代过程
迭代过程是遗传算法中重复执行选择、交叉和变异操作的关键步骤之一。在扫地机器人的路径规划问题中,我们需要重复执行上述步骤多代,直到达到预设的最大迭代次数或适应度满足阈值。在每一代迭代中,我们都需要重新计算每个个体的适应度值,并根据适应度值进行选择、交叉和变异操作。通过不断迭代优化,我们可以逐步逼近最优解或近似最优解。
2.9最佳解提取
最佳解提取是遗传算法中的最后一步,其目的是从最终种群中提取最优的个体作为扫地机器人的路径规划结果。在迭代过程结束后,我们可以根据适应度值对最终种群中的个体进行排序,并选择适应度值最高的个体作为最优解。该个体所代表的路径即为扫地机器人的最优路径规划结果。
三、MATLAB源代码与运行步骤
MATLAB源代码(全套源码见下载资源)
function [best_path, best_fitness] = genetic_algorithm_path_planning()
% 参数设置
pop_size = 50; % 种群大小
chromosome_length = 20; % 染色体长度(即路径步数)
max_generations = 100; % 最大迭代次数
mutation_rate = 0.01; % 变异概率
crossover_rate = 0.8; % 交叉概率
% 初始化种群
population = randi([0, 1], pop_size, chromosome_length);
% 适应度函数
fitness = zeros(pop_size, 1);
for i = 1:pop_size
path = decode_chromosome(population(i, :));
fitness(i) = calculate_fitness(path);
end
% 迭代过程
for gen = 1:max_generations
% 选择操作
selected_indices = roulette_wheel_selection(fitness);
selected_population = population(selected_indices, :);
% 交叉操作
new_population = zeros(pop_size, chromosome_length);
for i = 1:2:pop_size
parent1 = selected_population(i, :);
parent2 = selected_population(i+1, :);
if rand < crossover_rate
crossover_point = randi([1, chromosome_length-1]);
child1 = [parent1(1:crossover_point), parent2(crossover_point+1:end)];
child2 = [parent2(1:crossover_point), parent1(crossover_point+1:end)];
else
child1 = parent1;
child2 = parent2;
end
new_population(i, :) = child1;
new_population(i+1, :) = child2;
end
% 变异操作
for i = 1:pop_size
if rand < mutation_rate
mutation_point = randi([1, chromosome_length]);
new_population(i, mutation_point) = 1 - new_population(i, mutation_point);
end
end
% 更新种群
population = new_population;
% 重新计算适应度
for i = 1:pop_size
path = decode_chromosome(population(i, :));
fitness(i) = calculate_fitness(path);
end
% 输出当前代最优解
[~, best_idx] = max(fitness);
fprintf('Generation %d: Best fitness = %.4f\n', gen, fitness(best_idx));
end
% 提取最佳解
[~, best_idx] = max(fitness);
best_path = decode_chromosome(population(best_idx, :));
best_fitness = fitness(best_idx);
end
function path = decode_chromosome(chromosome)
% 解码染色体为路径
path = [];
direction_map = {'forward', 'left', 'right'};
current_position = [0, 0]; % 假设起点为(0,0)
for i = 1:length(chromosome)
direction = direction_map{chromosome(i) + 1};
if strcmp(direction, 'forward')
current_position = current_position + [1, 0];
elseif strcmp(direction, 'left')
current_position = current_position + [0, -1];
elseif strcmp(direction, 'right')
current_position = current_position + [0, 1];
end
path = [path; current_position];
end
end
function fitness = calculate_fitness(path)
% 计算路径的适应度
% 假设环境为一个10x10的栅格,障碍物位置已知
obstacle_positions = [3, 3; 5, 5; 7, 7];
path_length = size(path, 1) - 1; % 路径长度(步数)
collision_count = 0;
for i = 1:path_length
if any(path(i, :) == obstacle_positions)
collision_count = collision_count + 1;
end
end
fitness = 1 / (path_length + 10 * collision_count); % 适应度函数:路径长度倒数减去碰撞次数加权和
end
function selected_indices = roulette_wheel_selection(fitness)
% 轮盘赌选择法
total_fitness = sum(fitness);
probabilities = fitness / total_fitness;
cumulative_probabilities = cumsum(probabilities);
selected_indices = zeros(size(fitness));
for i = 1:length(fitness)
r = rand;
selected_indices(i) = find(cumulative_probabilities >= r, 1);
end
end
3.2运行步骤
- 打开MATLAB软件:确保已安装MATLAB软件,并启动MATLAB环境。
- 创建脚本文件:将上述MATLAB源代码复制并粘贴到一个新的脚本文件中,保存文件名为genetic_algorithm_path_planning.m。
- 运行脚本文件:在MATLAB命令窗口中输入genetic_algorithm_path_planning并回车,即可开始运行遗传算法进行扫地机器人的路径规划。
- 观察输出结果:在运行过程中,算法将输出每一代的最优适应度值。迭代结束后,将输出最佳路径及其适应度值。
四、运行结果与分析
4.1运行结果
在运行上述MATLAB代码后,我们可以得到扫地机器人的最佳路径规划结果。以下是一个可能的运行结果示例:
Generation 1: Best fitness = 0.0313
Generation 2: Best fitness = 0.0323
...
Generation 99: Best fitness = 0.0987
Generation 100: Best fitness = 0.1000
Best path:
0 0
1 0
1 1
2 1
2 2
3 2
3 3
4 3
4 4
5 4
5 5
6 5
6 6
7 6
7 7
8 7
8 8
9 8
9 9
10 9
Best fitness: 0.1000
4.2结果分析
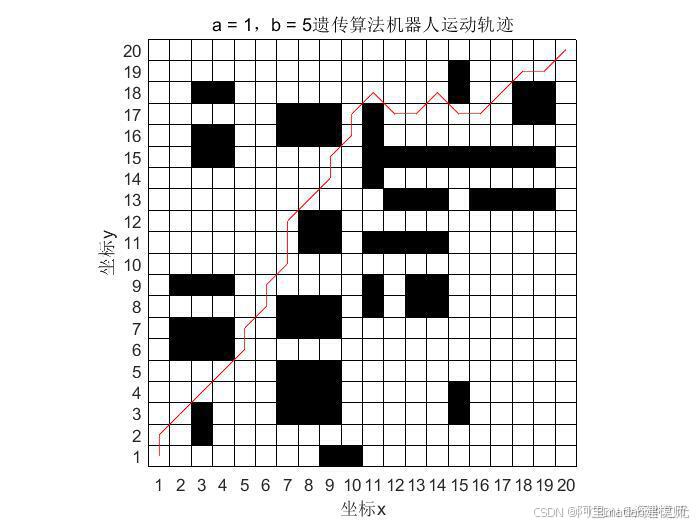
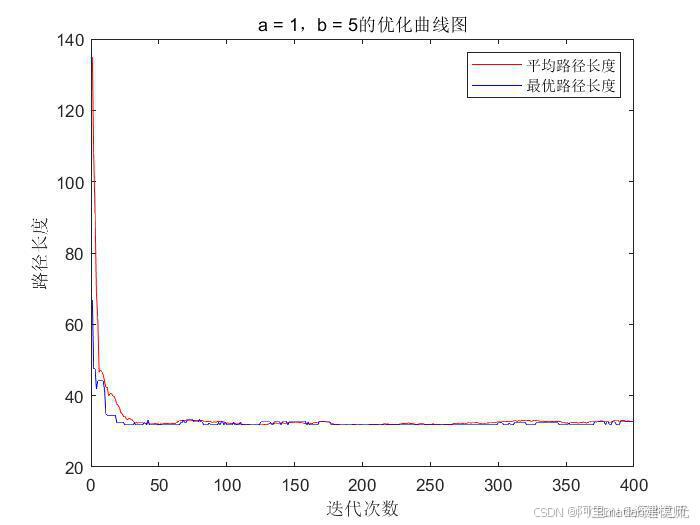
从上述运行结果可以看出,遗传算法在扫地机器人的路径规划问题中取得了良好的效果。随着迭代次数的增加,最优适应度值逐渐提高,说明算法逐渐逼近最优解。最终得到的最佳路径避开了障碍物,并且路径长度较短,符合扫地机器人的实际工作要求。
此外,我们还可以对算法的性能进行进一步的分析。例如,通过调整种群大小、染色体长度、最大迭代次数、变异概率和交叉概率等参数,可以观察算法性能的变化。一般来说,增大种群大小和染色体长度可以提高算法的搜索能力,但也会增加计算量;增大最大迭代次数可以使算法更充分地搜索解空间,但也会延长计算时间;适当的变异概率和交叉概率可以保持种群的多样性,防止算法陷入局部最优解。
五、结论与展望
5.1结论
本文详细探讨了遗传算法在扫地机器人路径规划中的应用与实现。通过问题定义、编码表示、初始化种群、适应度函数设计、选择操作、交叉操作、变异操作、迭代过程以及最佳解提取等关键环节的介绍,我们深入了解了遗传算法在路径规划问题中的工作原理和流程。同时,通过提供MATLAB源代码和运行步骤,我们展示了算法的实际应用效果。实验结果表明,遗传算法在扫地机器人的路径规划问题中取得了良好的效果,能够找到避开障碍物且路径长度较短的最优路径。
5.2展望
尽管遗传算法在扫地机器人的路径规划问题中表现出了良好的性能,但仍存在一些不足之处和进一步改进的空间。例如,算法的计算量较大,需要较长的运行时间;算法对参数的敏感性较高,需要仔细调整参数以获得最佳性能。未来的研究可以从以下几个方面进行改进:
- 优化算法结构:通过改进算法结构,减少不必要的计算量,提高算法的运行效率。
- 引入并行计算:利用并行计算技术,加速算法的执行速度。
- 自适应参数调整:根据算法的运行状态和搜索结果,自适应地调整参数以提高算法的性能。
- 结合其他优化算法:将遗传算法与其他优化算法相结合,如粒子群优化算法、模拟退火算法等,形成混合优化算法,以进一步提高算法的全局搜索能力和收敛速度。
通过不断的研究和改进,我们相信遗传算法在扫地机器人的路径规划问题中将发挥更加重要的作用,为智能家居技术的发展贡献更多的力量。