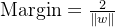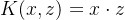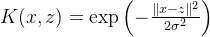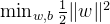支持向量机（Support Vector Machine, SVM）是一种常用的监督学习算法，主要用于分类问题和回归问题。它的核心思想是通过寻找一个超平面，将不同类别的样本分隔开，同时最大化分类边界（即分类超平面到最近样本点的距离），从而实现分类或预测的目的。

SVM的基本思想

1. 线性可分情况下：

   • 给定一个训练数据集 ，其中 是样本，是类别标签。

   • SVM的目标是寻找一个超平面：

     

     使得样本点被划分到超平面的两侧，并且两类样本之间的间隔（margin）最大化。

   • 间隔最大化：分类超平面到最近样本点的距离（即间隔）为：

     

     SVM通过最大化间隔来提高分类的鲁棒性。

2. 线性不可分情况下：

   • 对于线性不可分的数据，SVM引入核函数，将低维数据映射到高维空间，在高维空间中找到一个可以线性分割的超平面。
   • 常用的核函数有：
     • 线性核：
     • 多项式核：
     • 高斯核（RBF核）：

SVM的核心优化问题

SVM的优化目标是：

• 这里的约束条件保证了所有样本点都被正确分类，且满足间隔要求。

软间隔 SVM（Soft-Margin SVM）

当数据存在噪声或无法完全线性分割时，SVM引入松弛变量 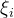 来允许一定的分类错误：

• C 是正则化参数，用于权衡间隔大小与分类错误之间的关系。

支持向量的概念

支持向量是指位于分类边界附近的样本点，这些样本点对超平面的确定起关键作用。超平面由这些支持向量决定，其他样本点的存在与否不会影响分类结果。

SVM的优点

1. 分类边界明确：
   • 通过最大化间隔，SVM在理论上具有更好的泛化能力。
2. 适用于高维数据：
   • 通过核函数，SVM能够在高维空间中找到非线性分类边界。
3. 对小样本数据效果好：
   • 在样本较少时，SVM的性能往往优于其他算法。

SVM的缺点

1. 对大规模数据较慢：
   • SVM的时间复杂度随着样本数量的增加而显著提升。
2. 参数调优复杂：
   • 正则化参数 C 和核函数参数（如 RBF 的 σ ）需要仔细调整。
3. 对非平衡数据敏感：
   • 如果类别不平衡，可能导致分类结果偏向多数类。

应用场景

1. 文本分类（如垃圾邮件过滤）。
2. 图像分类（如人脸识别）。
3. 生物信息学（如基因分类）。
4. 医学诊断（如肿瘤分类）。

小结

SVM是一种基于间隔最大化的强大分类算法，通过核函数可以扩展到非线性分类任务。尽管在大规模数据和参数调优方面存在一定局限性，但它在高维、小样本和特征少的数据集上具有出色表现。