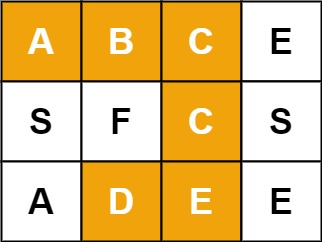
1. 字母迷宫
字母迷宫游戏初始界面记作 m x n 二维字符串数组 grid,请判断玩家是否能在 grid 中找到目标单词 target。
注意:寻找单词时 必须 按照字母顺序,通过水平或垂直方向相邻的单元格内的字母构成,同时,同一个单元格内的字母 不允许被重复使用 。
示例 1:
输入:grid = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], target = "ABCCED" 输出:true
示例 2:
输入:grid = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], target = "SEE" 输出:true
示例 3:
输入:grid = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], target = "ABCB" 输出:false
提示:
m == grid.length
n = grid[i].length
1 <= m, n <= 6
1 <= target.length <= 15
grid 和 target 仅由大小写英文字母组成
解题思路解析
核心思想
这是一道典型的回溯问题,使用深度优先搜索(DFS)+ 剪枝可以高效解决。解题流程主要分为以下几个步骤:
-
深度优先搜索 (DFS):
- 将问题转化为矩阵中每个单元格作为起点,从四个方向递归搜索是否可以匹配目标字符串
target。 - 递归过程模拟“暴力法”搜索,沿路径尝试匹配字符串的每个字符。
- 将问题转化为矩阵中每个单元格作为起点,从四个方向递归搜索是否可以匹配目标字符串
-
剪枝:
- 遇到显然无法完成匹配的路径时提前终止递归(如字符不匹配或超出矩阵范围)。
- 剪枝操作避免了无效的重复计算,提高了效率。
具体步骤
- 遍历矩阵
grid的每个单元格,尝试作为匹配的起点。 - 对每个起点使用深度优先搜索:
- 若当前单元格匹配目标字符串的某字符,递归检查四个方向是否能够继续匹配。
- 在递归时使用标记法避免重复访问当前路径中的元素。
- 若匹配到
target的最后一个字符,则返回成功。
- 若所有起点均无法匹配目标字符串,则返回
false。
DFS 的参数与递推关系
- 递归参数:
i, j:当前搜索到的矩阵元素的行列索引。k:目标字符串target当前匹配到的字符索引。
- 终止条件:
- 失败:当前索引越界,当前元素与目标字符不匹配,或当前元素已被访问过。
- 成功:已匹配到
target的最后一个字符。
- 递推:
- 标记当前元素为已访问(临时修改其值)。
- 递归搜索上下左右四个方向。
- 恢复当前元素的初始值。
代码详解(Java)
class Solution {
public boolean wordPuzzle(char[][] grid, String target) {
// 将目标字符串转化为字符数组
char[] words = target.toCharArray();
// 遍历每个矩阵单元格作为起点
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
// 从当前单元格启动 DFS,若找到路径,返回 true
if (dfs(grid, words, i, j, 0)) return true;
}
}
return false; // 遍历所有起点后仍未找到路径
}
boolean dfs(char[][] grid, char[] target, int i, int j, int k) {
// 越界检查或当前元素不匹配,返回 false
if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] != target[k]) {
return false;
}
// 如果匹配到目标字符串的最后一个字符,返回 true
if (k == target.length - 1) return true;
// 临时标记当前单元格为已访问
char temp = grid[i][j];
grid[i][j] = '\0';
// 递归检查四个方向是否能匹配后续字符
boolean res = dfs(grid, target, i + 1, j, k + 1) || // 下
dfs(grid, target, i - 1, j, k + 1) || // 上
dfs(grid, target, i, j + 1, k + 1) || // 右
dfs(grid, target, i, j - 1, k + 1); // 左
// 恢复当前单元格的值
grid[i][j] = temp;
return res; // 返回结果
}
}
复杂度分析
-
时间复杂度:
- 最差情况下,矩阵中每个单元格都作为起点,且每个字符递归搜索 3 个方向,复杂度为 O(3K⋅MN)O(3^K \cdot MN)。
- KK 为目标字符串
target的长度,M,NM, N 为矩阵的行列大小。
-
空间复杂度:
- 递归深度最大为字符串长度 KK,因此空间复杂度为 O(K)O(K)。
总结
- 本算法利用了回溯思想,通过递归模拟暴力搜索并结合剪枝优化,适用于类似路径搜索的问题。
- 使用矩阵单元格的临时修改(标记法)避免了额外的访问记录数据结构,简化了代码逻辑并提升了效率。
2. 衣厨整理
家居整理师将待整理衣橱划分为 m x n 的二维矩阵 grid,其中 grid[i][j] 代表一个需要整理的格子。整理师自 grid[0][0] 开始 逐行逐列 地整理每个格子。
整理规则为:在整理过程中,可以选择 向右移动一格 或 向下移动一格,但不能移动到衣柜之外。同时,不需要整理 digit(i) + digit(j) > cnt 的格子,其中 digit(x) 表示数字 x 的各数位之和。
请返回整理师 总共需要整理多少个格子。
示例 1:
输入:m = 4, n = 7, cnt = 5 输出:18
提示:
1 <= n, m <= 1000 <= cnt <= 20
前置工作:数位和计算
- 利用
x % 10提取个位数,x / 10实现高位右移,可以高效地求出任意数字的数位和。 - 对于连续数字,可以采用增量计算避免重复求和:
- 若
(x+1) % 10 == 0(进位):数位和减少 8。 - 否则:数位和加 1。
- 若
- 数位和增量的公式使得在大规模矩阵中快速更新成为可能。
DFS 方法
算法思路
- 递归搜索:从起点
(0,0)出发,优先向右和向下探索,沿路径记录所有可达解。 - 剪枝优化:
- 若当前坐标越界或数位和超出限制,立即返回。
- 若当前格子已访问过,也不再重复探索。
- 回溯操作:每次递归返回当前路径的总可达解数。
优点
- 实现简单,适合处理连通区域的深度探索。
代码补充
以下是对代码中逻辑的分步解释:
public int dfs(int i, int j, int si, int sj) {
// 剪枝条件:越界、数位和超出限制、已访问
if (i >= m || j >= n || cnt < si + sj || visited[i][j]) return 0;
// 标记当前格子已访问
visited[i][j] = true;
// 递归计算当前格子及其右、下方向的总解
return 1
+ dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj)
+ dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8);
}
BFS 方法
算法思路
- 队列辅助:采用队列保存当前所有待探索的节点,每次从队首取出当前节点进行处理,并将其相邻的未访问节点加入队列。
- 终止条件:队列为空,表明所有可能的路径均已探索完毕。
优点
- 自然支持“逐层平推”的搜索方式,更适合多层嵌套结构的遍历。
代码补充
以下是 BFS 的关键代码及逻辑说明:
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[] { 0, 0, 0, 0 }); // 起点入队
while (!queue.isEmpty()) {
int[] x = queue.poll();
int i = x[0], j = x[1], si = x[2], sj = x[3];
// 剪枝条件:越界、数位和超出限制、已访问
if (i >= m || j >= n || cnt < si + sj || visited[i][j]) continue;
// 标记当前格子已访问,更新解的数量
visited[i][j] = true;
res++;
// 将右、下方向的格子加入队列
queue.add(new int[] { i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj });
queue.add(new int[] { i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8 });
}
复杂度分析
- 时间复杂度:两种方法均为 O(M×N)),最坏情况下机器人遍历整个矩阵。
- 空间复杂度:
- DFS:递归栈的深度在最坏情况下为 O(M+N)O(M + N),辅助矩阵占用 O(M×N)。
- BFS:队列大小与矩阵中未访问格子的数量成正比,最坏情况为 O(M×N)。
方法对比
| 方法 | 优点 | 缺点 |
|---|---|---|
| DFS | 实现简单,适合递归思维的场景 | 遇到大规模数据时递归栈溢出风险 |
| BFS | 每层搜索有序,不易遗漏或重复访问 | 实现稍复杂,占用额外队列空间 |
总结
这两种方法针对机器人运动范围问题提供了两种视角的解决方案:
- 若矩阵规模较小或路径连通性较强,DFS 更加直观;
- 若矩阵规模较大或需要层次化搜索,BFS 的性能和可靠性更高。
3. 螺旋遍历二维数组
给定一个二维数组 array,请返回「螺旋遍历」该数组的结果。
螺旋遍历:从左上角开始,按照 向右、向下、向左、向上 的顺序 依次 提取元素,然后再进入内部一层重复相同的步骤,直到提取完所有元素。
示例 1:
输入:array = [[1,2,3],[8,9,4],[7,6,5]] 输出:[1,2,3,4,5,6,7,8,9]
示例 2:
输入:array = [[1,2,3,4],[12,13,14,5],[11,16,15,6],[10,9,8,7]] 输出:[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
解题思路
-
边界初始化
定义矩阵的四个边界:l(left):左边界,初始为 0。r(right):右边界,初始为矩阵的列数减一。t(top):上边界,初始为 0。b(bottom):下边界,初始为矩阵的行数减一。
-
遍历方向 模拟顺时针遍历矩阵的过程,按照如下顺序循环:
- 从左到右:固定行
t,从l遍历到r。 - 从上到下:固定列
r,从t+1遍历到b。 - 从右到左(如果还有剩余行):固定行
b,从r-1遍历到l。 - 从下到上(如果还有剩余列):固定列
l,从b-1遍历到t+1。
- 从左到右:固定行
-
边界收缩 每次打印后,更新相应的边界:
- 左边界
l向右收缩:l++ - 右边界
r向左收缩:r-- - 上边界
t向下收缩:t++ - 下边界
b向上收缩:b--
- 左边界
-
终止条件 当上下边界 (
t > b) 或左右边界 (l > r) 交错时,停止打印。
Java 实现
以下是 Java 实现的逐步解析:
class Solution {
public int[] spiralArray(int[][] array) {
// 处理空矩阵的情况
if (array.length == 0) return new int[0];
// 初始化边界
int l = 0, r = array[0].length - 1; // 左边界和右边界
int t = 0, b = array.length - 1; // 上边界和下边界
int x = 0; // 结果数组的索引
int[] res = new int[(r + 1) * (b + 1)]; // 初始化结果数组
// 循环打印矩阵
while (true) {
// 从左到右
for (int i = l; i <= r; i++) res[x++] = array[t][i];
if (++t > b) break; // 收缩上边界,判断是否越界
// 从上到下
for (int i = t; i <= b; i++) res[x++] = array[i][r];
if (l > --r) break; // 收缩右边界,判断是否越界
// 从右到左
for (int i = r; i >= l; i--) res[x++] = array[b][i];
if (t > --b) break; // 收缩下边界,判断是否越界
// 从下到上
for (int i = b; i >= t; i--) res[x++] = array[i][l];
if (++l > r) break; // 收缩左边界,判断是否越界
}
// 返回结果数组
return res;
}
}
复杂度分析
-
时间复杂度
- 每个元素都被访问一次,总共有
M × N个元素。 - 时间复杂度为
O(M × N)。
- 每个元素都被访问一次,总共有
-
空间复杂度
- 只使用了四个整型变量(
l, r, t, b)来表示边界,额外空间复杂度为O(1)。
- 只使用了四个整型变量(
测试示例
示例 1
输入:
int[][] array = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
输出:
[1, 2, 3, 6, 9, 8, 7, 4, 5]
示例 2
输入:
int[][] array = {{1, 2}, {3, 4}};
输出:
[1, 2, 4, 3]
小结
- 该解法利用了模拟法,通过控制边界逐步收缩来实现顺时针打印矩阵。
- 在写代码时,注意边界条件的判断(例如数组越界问题)。
- 本解法具有较高的时间和空间效率,适用于各种大小的矩阵。