背景
变分量子算法是用于观察嘈杂的近期设备上的量子计算效用的有前途的候选混合算法。变分算法的特点是使用经典优化算法迭代更新参数化试验解决方案或“拟设”。这些方法中最重要的是变分量子特征求解器 (VQE),它旨在求解给定汉密尔顿量的基态,该汉密尔顿量表示为泡利项的线性组合,其中拟设电路中要优化的参数数量是量子比特数量的多项式。鉴于完整解决方案向量的大小是量子比特数量的指数,使用 VQE 成功最小化通常需要额外的问题特定信息来定义拟设电路的结构。
执行 VQE 算法需要以下组件:汉密尔顿量和假设(问题规范)Qiskit 运行时估计器经典优化器虽然汉密尔顿量和假设需要特定领域的知识来构建,但这些细节对于运行时来说并不重要,我们可以以相同的方式执行广泛的 VQE 问题。
步骤 1 .将经典输入映射到量子问题
尽管 VQE 算法所讨论的问题实例可能来自各种领域,但通过 Qiskit Runtime 执行的形式是相同的。Qiskit 提供了一个方便的类,用于以泡利形式表达汉密尔顿量,并在 qiskit.circuit.library 中提供了一组广泛使用的假设电路。
这个示例汉密尔顿量源自量子化学问题。
设置
# 导入 VQE 实验所需的工具。ansatz是训练电路。
# General imports
import numpy as np
# Pre-defined ansatz circuit and operator class for Hamiltonian
from qiskit.circuit.library import EfficientSU2
from qiskit.quantum_info import SparsePauliOp
# SciPy minimizer routine
from scipy.optimize import minimize
# Plotting functions
import matplotlib.pyplot as plt#runtime和session两个类用于管理与 IBM Quantum 运行时服务的连接和会话。
#Estimator类用于估算量子电路运行的期望值,通常用于量子算法中的成本函数评估。
from qiskit_ibm_runtime import QiskitRuntimeService, Session
from qiskit_ibm_runtime import EstimatorV2 as Estimator
# 从可用的后端中选择一个负载最少的后端,以便提交作业,即调用真实量子计算机
service = QiskitRuntimeService(channel="ibm_quantum")
backend = service.least_busy(operational=True, simulator=False)
# SparsePauliOp 类从给定的 Pauli 表达式和系数创建哈密顿量
hamiltonian = SparsePauliOp.from_list(
[("YZ", 0.3980), ("ZI", -0.3980), ("ZZ", -0.0113), ("XX", 0.1810)]
)选择的假设是 EfficientSU2,它默认以线性方式纠缠量子位,使其成为连接有限的量子硬件的理想选择。
ansatz = EfficientSU2(hamiltonian.num_qubits)
ansatz.decompose().draw("mpl", style="iqp")num_params = ansatz.num_parameters
这里使用的num_params数为16,即16个量子门。
步骤 2. 优化量子执行问题
为了减少总作业执行时间,Qiskit 原语仅接受符合目标 QPU 支持的指令和连接的电路(ansatz)和可观察量(Hamiltonian)(称为指令集架构 (ISA) 电路和可观察量)。
ISA 电路安排一系列 qiskit.transpiler 传递以优化所选后端的电路并使其与后端的 ISA 兼容。这可以通过 qiskit.transpiler 中的预设传递管理器及其optimization_level 参数轻松完成。
最低优化级别执行使电路在设备上运行所需的最少操作;它将电路量子位映射到设备量子位并添加交换门以允许所有两量子位操作。最高优化级别更加智能,并使用了许多技巧来减少总门数。由于多量子位门具有高错误率并且量子位会随着时间的推移而退相干,因此较短的电路应该会给出更好的结果。
#这个函数用于生成预设的电路优化处理器。
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager
#pm 使用指定的目标信息生成一个预设的优化处理器(pass manager)
target = backend.target
pm = generate_preset_pass_manager(target=target, optimization_level=3)
ansatz_isa = pm.run(ansatz)
ansatz_isa.draw(output="mpl", idle_wires=False, style="iqp")
在使用 Runtime Estimator V2 运行作业之前,转换汉密尔顿函数以使其与后端兼容。使用 SparsePauliOp 对象的 apply_layout 方法执行转换
步骤 3. 使用 Qiskit 原语执行
与许多经典优化问题一样,VQE 问题的解可以表述为标量成本函数的最小化。根据定义,VQE 通过优化假设电路参数来最小化汉密尔顿量的期望值(能量),从而寻找汉密尔顿量的基态解。由于 Qiskit 运行时估算器直接采用汉密尔顿量和参数化的假设,并返回必要的能量,因此 VQE 实例的成本函数非常简单。
注意,Qiskit Runtime EstimatorV2 的 run() 方法采用原始统一块 (PUB) 的可迭代对象。每个 PUB 都是一个可迭代对象,格式为 (circuit, observables, paramter_values: Optional, precision: Optional)。
#定义一个损失函数
def cost_func(params, ansatz, hamiltonian, estimator):
"""Return estimate of energy from estimator
Parameters:
params (ndarray): Array of ansatz parameters
ansatz (QuantumCircuit): Parameterized ansatz circuit
hamiltonian (SparsePauliOp): Operator representation of Hamiltonian
estimator (EstimatorV2): Estimator primitive instance
cost_history_dict: Dictionary for storing intermediate results
Returns:
float: Energy estimate
"""
pub = (ansatz, [hamiltonian], [params])
result = estimator.run(pubs=[pub]).result()
energy = result[0].data.evs[0]
cost_history_dict["iters"] += 1
cost_history_dict["prev_vector"] = params
cost_history_dict["cost_history"].append(energy)
print(f"Iters. done: {cost_history_dict['iters']} [Current cost: {energy}]")
return energy请注意,除了必须作为第一个参数的优化参数数组之外,使用其他参数来传递成本函数中所需的项,例如 cost_history_dict 。此字典存储每次迭代的当前向量,例如,以防万一由于失败而需要重新启动例程,还返回当前迭代次数和每次迭代的平均时间。
cost_history_dict = {
"prev_vector": None,
"iters": 0,
"cost_history": [],
}
x0 = 2 * np.pi * np.random.random(num_params) 选择的经典优化器来最小化成本函数。在这里,我们通过最小化函数使用 SciPy 中的 COBYLA 例程。请注意,在实际量子硬件上运行时,优化器的选择很重要,因为并非所有优化器都能同样好地处理嘈杂的成本函数景观。
要开始例程,请指定一组随机初始参数:
因为我们要发送大量想要一起执行的作业,所以我们使用 Session 在一个块中执行所有生成的电路。这里的 args 是提供成本函数所需的附加参数的标准 SciPy 方法。
with Session(backend=backend) as session:
estimator = Estimator(mode=session)
estimator.options.default_shots = 10000
res = minimize(
cost_func,
x0,
args=(ansatz_isa, hamiltonian_isa, estimator),
method="cobyla",
)在此例程的末尾,我们得到了标准 SciPy OptimizeResult 格式的结果。由此我们可以看出,需要进行 nfev 次成本函数评估才能获得参数角度 (x) 的解向量,当将其插入 ansatz 电路时,就会产生我们正在寻找的近似基态解。
输出
message: Optimization terminated successfully.
success: True
status: 1
fun: -0.634701203143904
x: [ 2.581e+00 4.153e-01 ... 1.070e+00 3.123e+00]
nfev: 146
maxcv: 0.0步骤 4. 后处理,以经典格式返回结果
如果过程正确终止,则 cost_history_dict 字典中的 prev_vector 和 iters 值应分别等于解向量和函数求值总数。这很容易验证:
all(cost_history_dict["prev_vector"] == res.x)
cost_history_dict["iters"] == res.nfev
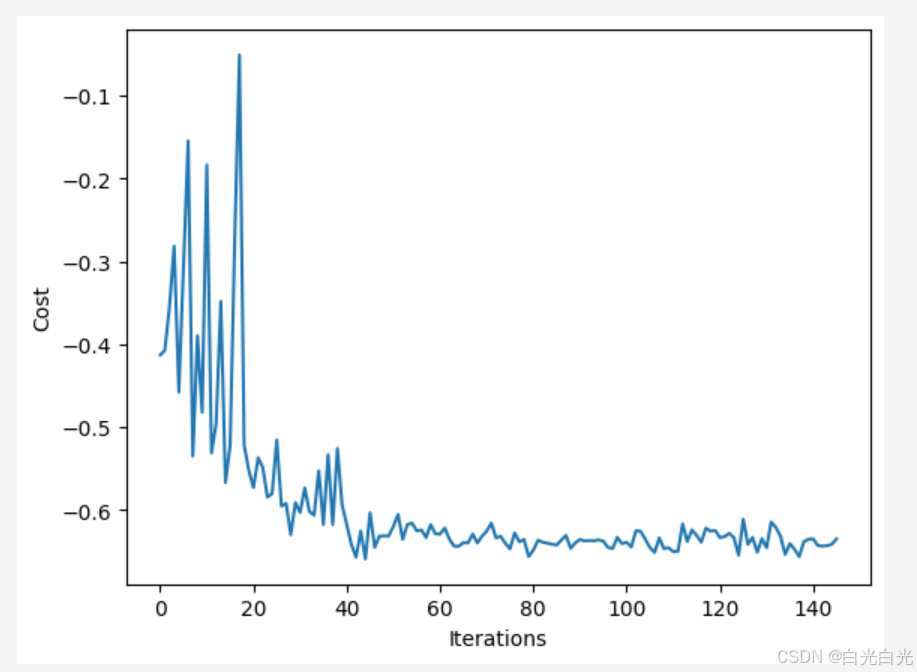
fig, ax = plt.subplots()
ax.plot(range(cost_history_dict["iters"]), cost_history_dict["cost_history"])
ax.set_xlabel("Iterations")
ax.set_ylabel("Cost")
plt.draw()理想状态下,即完成一整轮次的优化,模型成功收敛,代价趋于稳定。