描述
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7] 输出:3 解释:最长连续递增序列是 [1,3,5], 长度为3。 尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2] 输出:1 解释:最长连续递增序列是 [2], 长度为1。
提示:
1 <= nums.length <= 104-109 <= nums[i] <= 109
双指针
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
l = 0 # 左指针初始化为0
r = 0 # 右指针初始化为0
maxlen = 0 # 用于存储最长连续递增子序列的长度
while r < len(nums): # 当右指针没有越界时,继续循环
if r == l or nums[r - 1] < nums[r]: # 如果右指针和左指针相同或者当前元素大于前一个元素
maxlen = max(maxlen, r - l + 1) # 更新最长连续递增子序列的长度
r += 1 # 右指针右移
else:
l = r # 左指针移动到右指针的位置,重新开始寻找新的子序列
return maxlen # 返回最长连续递增子序列的长度
双指针(Two Pointers)(该部分原作:双指针算法以及滑动窗口Python(及其相关题目))
指的是在遍历元素的过程中,不是使用单个指针进行访问,而是使用两个指针进行访问,从而达到相应的目的。时间复杂度从O(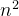
双指针分为「对撞指针」、「快慢指针」、「分离双指针」。
对撞指针
两个指针方向相反。两个指针left,right分别指向第一个元素和最后一个元素,然后left指针不断递增,right不断递减,直到两个指针相撞或达到其他条件为止.适合解决查找有序数组中满足某些约束条件的一组元素问题、字符串反转问题。
步骤
1. 使用两个指针left,right分别指向第一个元素和最后一个元素
2. 在循环体中将左右指针相向移动,当满足一定条件时,将左指针右移(+1);当满足一些条件时,将右指针左移(-1)
3. 直到两指针相撞或满足其他特殊条件时,跳出循环体
适用范围(有序数组或字符串问题):
1. 查找有序数组中满足某些约束条件的一组元素问题:比如二分查找、数字之和等问题
2. 字符串反转问题:反转字符串、回文数、颠倒二进制等问题,
3. 盛最多水的容器
伪代码
left = 0
right = len(nums) - 1
while left < right:
if 满足要求的特殊条件:
return 符合条件的值
elif 一定条件1:
left += 1
elif 一定条件2:
right -= 1
return 没找到
快慢指针:
两个指针方向相同。:两个指针从同一侧开始遍历序列,且移动的步长一个快一个慢。移动快的指针被称为快指针(fast),移动慢的指针被称为慢指针(slow)。两个指针以不同速度、不同策略移动,直到快指针移动到数组尾端,或者两指针相交,或者满足其他特殊条件时为止。适合解决数组中的移动、删除元素问题,或者链表中的判断是否有环、长度问题。
步骤:
1. 使用两个指针slow和fast.slow一般指向序列的第一个元素(slow = 0), fast一般指向序列的第二个元素(fast = 1)
2. 在循环体中将快慢指针向右移动.当满足一定条件时,将慢指针右移(+1), 当满足另一些条件时,将快指针右移(+1)
3.到快指针移动到数组尾端(即 fast == len(nums) - 1),或者两指针相交,或者满足其他特殊条件时跳出循环体
伪代码:
slow = 0
fast = 1
while 没有遍历完:
if 满足一些条件:
slow += 1
fast += 1
return ans
分离双指针
两个指针分别属于不同的数组 / 链表,两个指针分别在两个数组 / 链表中移动。适合解决有序数组合并,求交集、并集问题。
步骤:
1. 使用两个指针left_1, left_2.left_1指向第一个数组的第一个元素(left_1 = 0),left_2指向第二个数组的第二个元素(left_2 = 0)
2. 当满足一些条件时,两个指针同时右移(left_1 += 1, left_2 += 1)
3. 当满足另外一些条件是,left_1右移(left_1 += 1)
4. 当满足其它一些条件时,left_2右移(left_2 += 1)
5. 当其中一个数组遍历完或一些其他条件时跳出循环
伪代码:
left_1 = 0
left_2 = 0
while left_1 < len(nums1) and left_2 < len(nums2):
if 一定条件 1:
left_1 += 1
left_2 += 2
elif 一定条件 2:
left_1 += 1
elif 一定条件 3:
left_2 += 1
错误代码(骗分版)
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
lis = []
if len(set(nums)) == 1:
return 1
else:
temp = min(nums)
for i in range(len(nums)):
if nums[i] > temp:
temp = nums[i]
lis.append(nums[i])
else:
continue
return len(lis)
类动态规划
子数组问题,一般常用套路:
子数组必须以 i 位置结尾时的答案是啥;
如果每个位置都能结算一个答案,最终的答案必是其中的max。所以,定义DP:
dp[i]含义:必须以 i 位置结尾的子数组中,最长递增子数组的长度是多少。
dp[i] = nums[i] > nums[i-1] ? dp[i-1] + 1 : 1;
ans = max { dp[i] }
时间复杂度:O(n)
空间复杂度:O(1)class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
if nums is None or len(nums) == 0: # 检查输入列表是否为空或为None
return 0 # 如果为空或为None,返回0
pre = 1 # 用于存储当前连续递增子序列的长度,初始值为1
ans = pre # 用于存储最长连续递增子序列的长度,初始值为1
for i in range(1, len(nums)): # 从列表的第二个元素开始遍历
cur = 1 # 当前连续递增子序列的长度初始化为1
if nums[i] > nums[i - 1]: # 如果当前元素大于前一个元素
cur += pre # 当前连续递增子序列的长度加上前一个子序列的长度
ans = max(ans, cur) # 更新最长连续递增子序列的长度
pre = cur # 更新前一个子序列的长度为当前子序列的长度
return ans # 返回最长连续递增子序列的长度