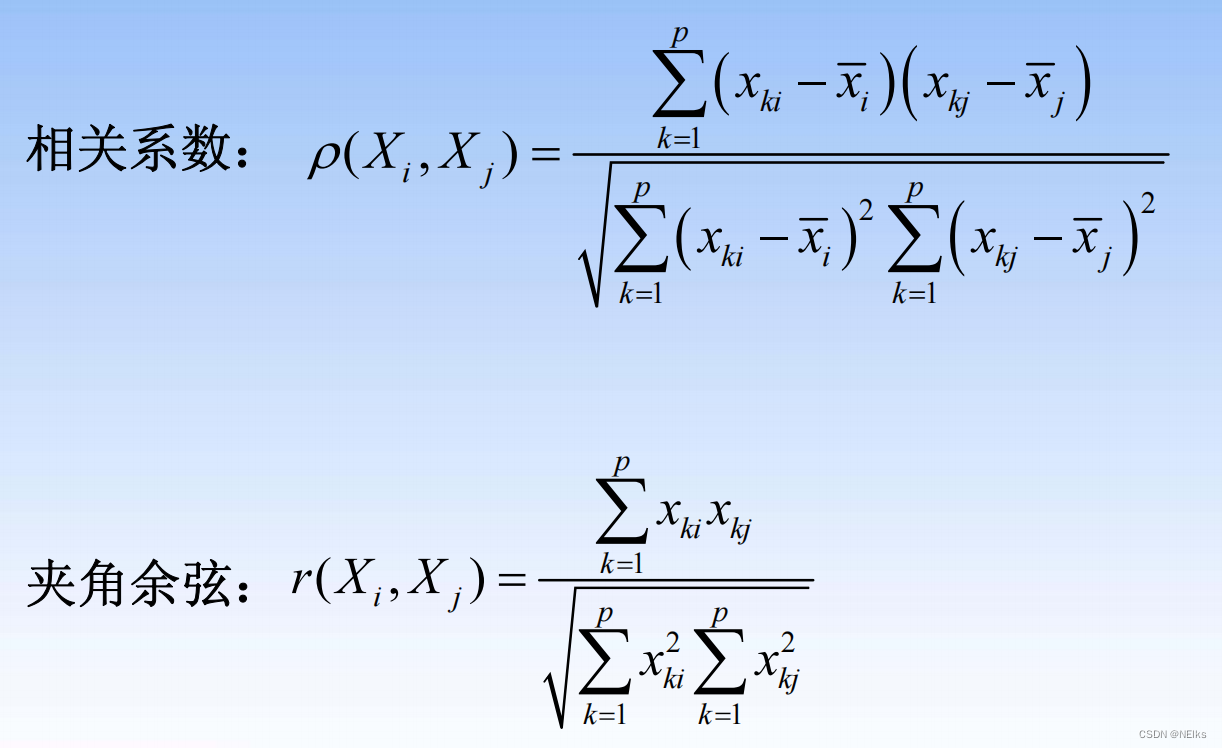目录
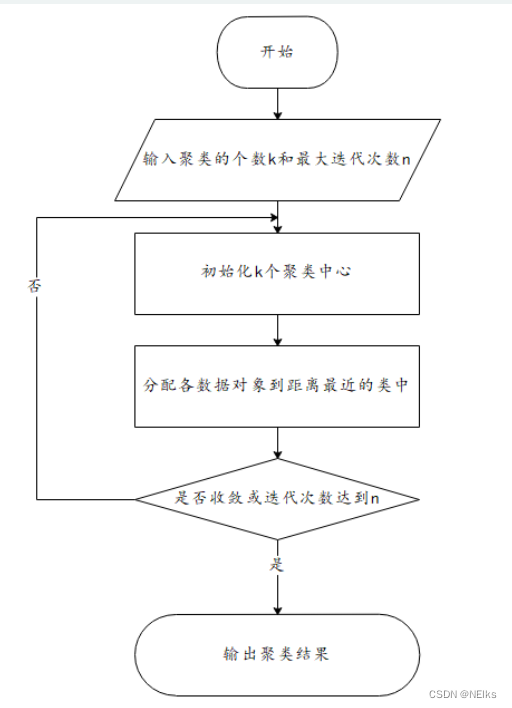
K-means聚类算法
步骤
- 指定簇个数 K 即分类类别个数
- 指定 K 个初始聚类中心
- 计算其余各点到聚类中心的距离,并重新划分样本点到离自己最近的簇类中
- 重新计算各个簇的中心作为新的聚类中心
- 循环上两步,直到中心收敛 或 达到指定的迭代次数
优点:
(1)算法简单、快速。
(2)对处理大数据集,该算法是相对高效率的。
缺点:
(1)要求用户必须事先给出要生成的簇的数目
K
。
(
2
)对初值敏感。
(
3
)对于孤立点数据敏感。
K-means++可解决后两个缺点:K-mean++需要 保证聚类中心尽可能远,所以远离其他点的孤立点很可能成为聚类中心,这样可以让孤立点单独在一个分类中;同时 K-means++ 保证聚类中心尽量远,保证了对初值的选择并不随意
K-means++
基本原则:优化了初始聚类中心的随机选取,需要初始聚类中心尽可能远
步骤
- 随机选取一个样本点作为第一个聚类中心
- 计算其余样本点与已有聚类中心的距离(若已有多个聚类中心,则先计算这些聚类中心的中心,再计算其余样本点与该中心的距离),距离越大,则被选为下一个聚类中心的概率越大(赋值一个概率),再用轮盘法抽出下一个聚类中心
- 重复直到选出 K 个初始聚类中心
- 继续K-means的步骤
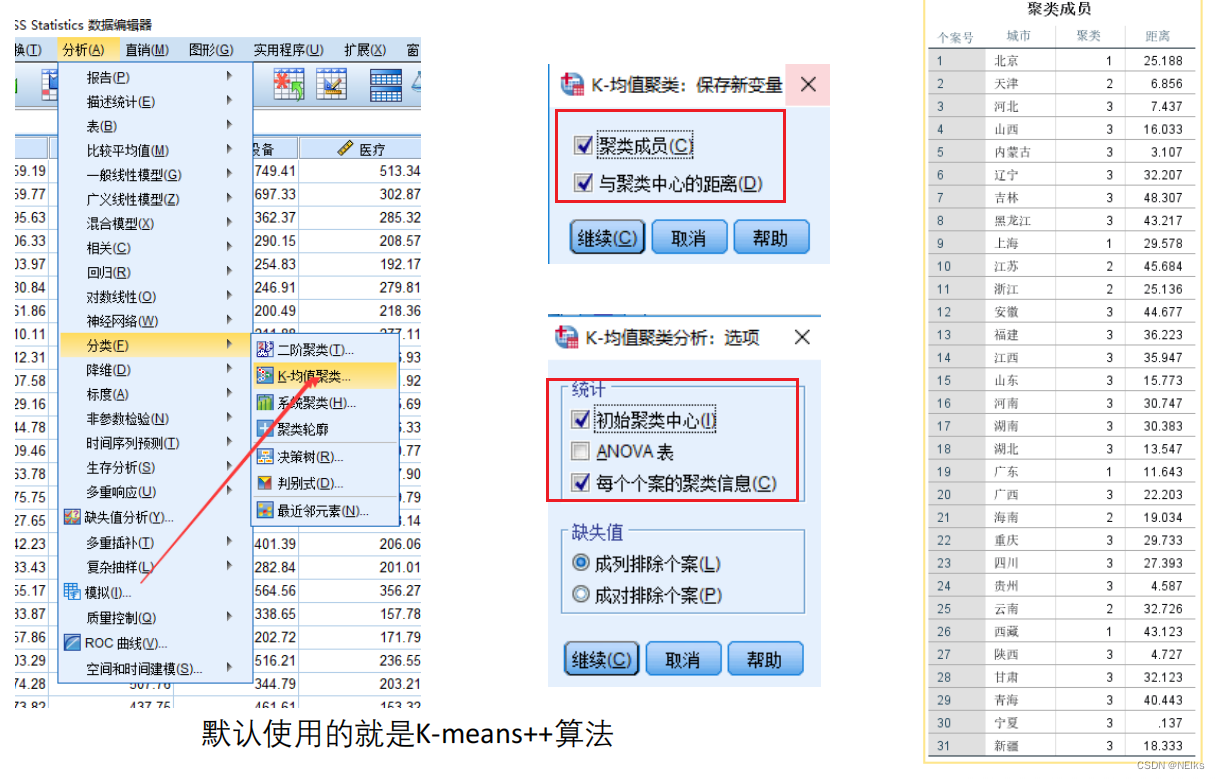
SPSS
存在的问题:
- 但上述两方法都不能解决要人为指定 K 的问题,只能多试几个 K 看哪个结果好解释
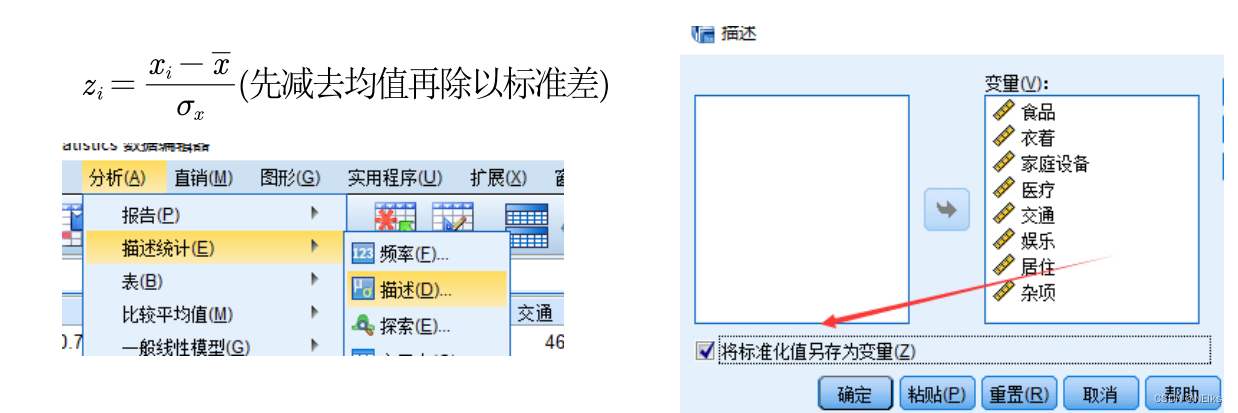
- 量纲的影响,将数据标准化
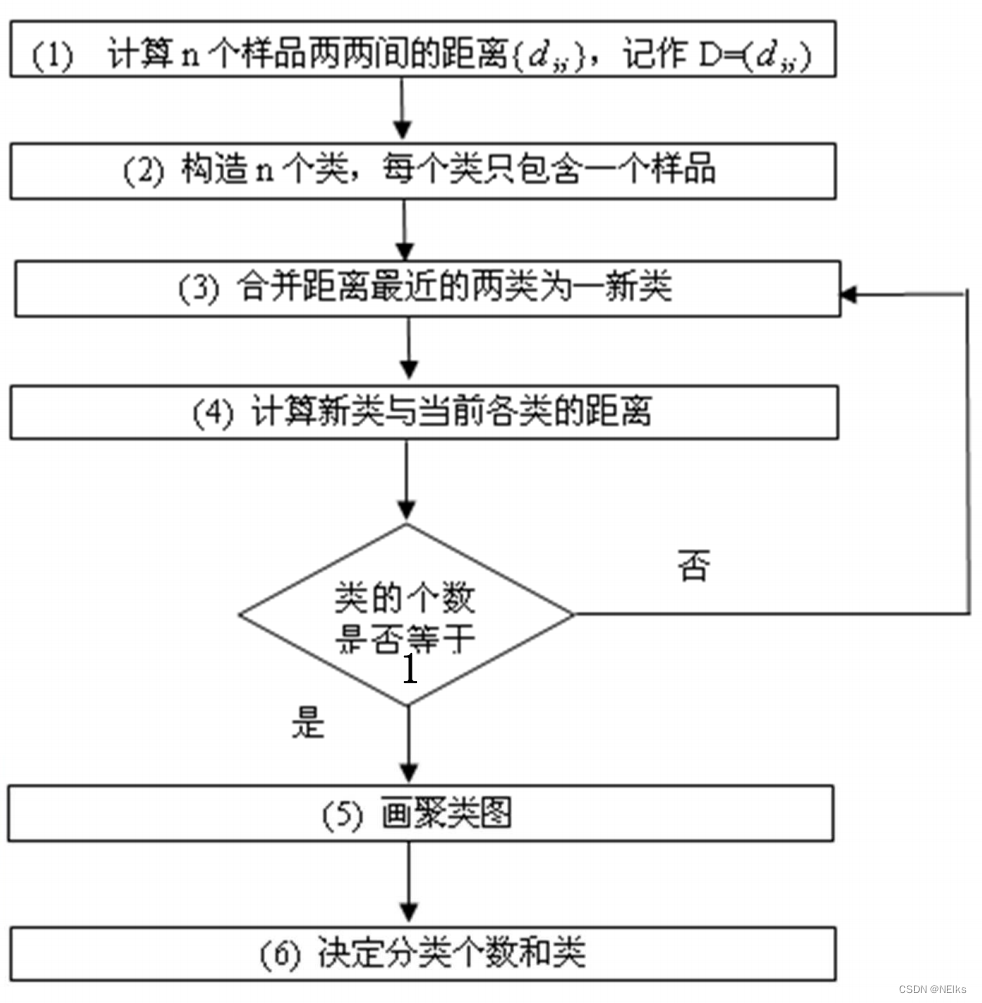
系统(层次)聚类
步骤
- 初始时候每个样本作为一个类,计算样本点之间的距离;
- 距离最小的两个合并为一个新类;
- 重新计算新类与所有类之间的距离,计算类之间的距离;
- 重复直到只有一个类
已知60个学生的6门成绩
对样本进行聚类:如对学生进行分类
对指标进行聚类:如把这六门课程分类
样本间的常用距离
指标间的距离
类与类之间的距离
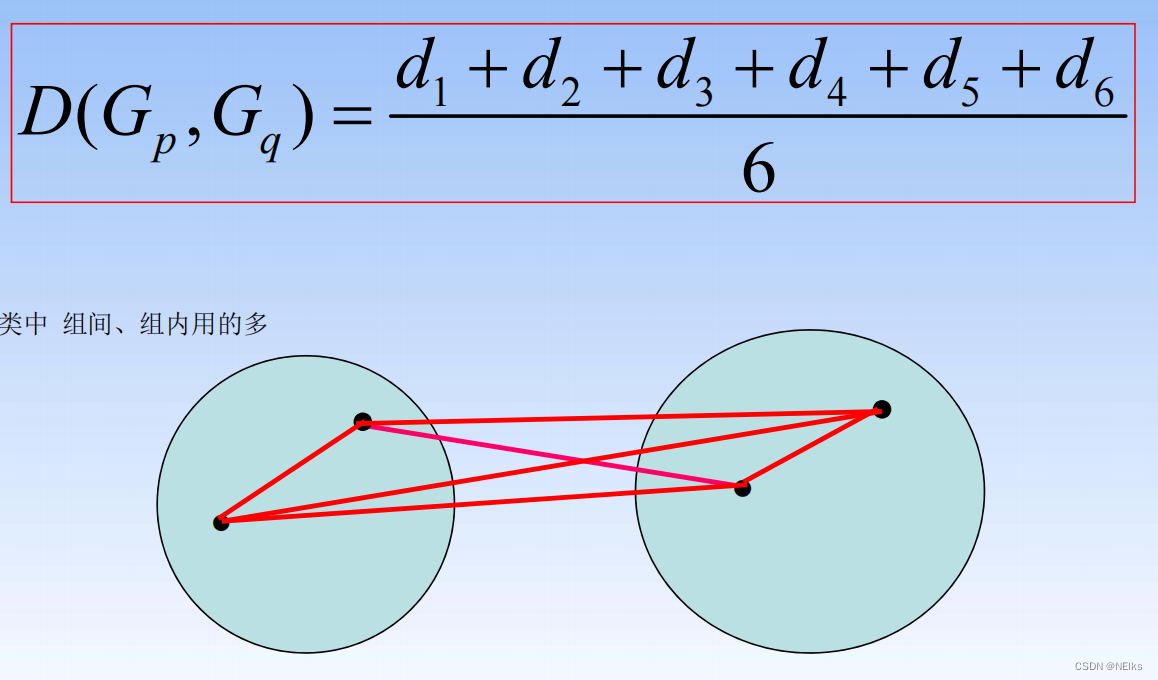
组间、组内用的多
最短距离法:
(Nearest Neighbor)

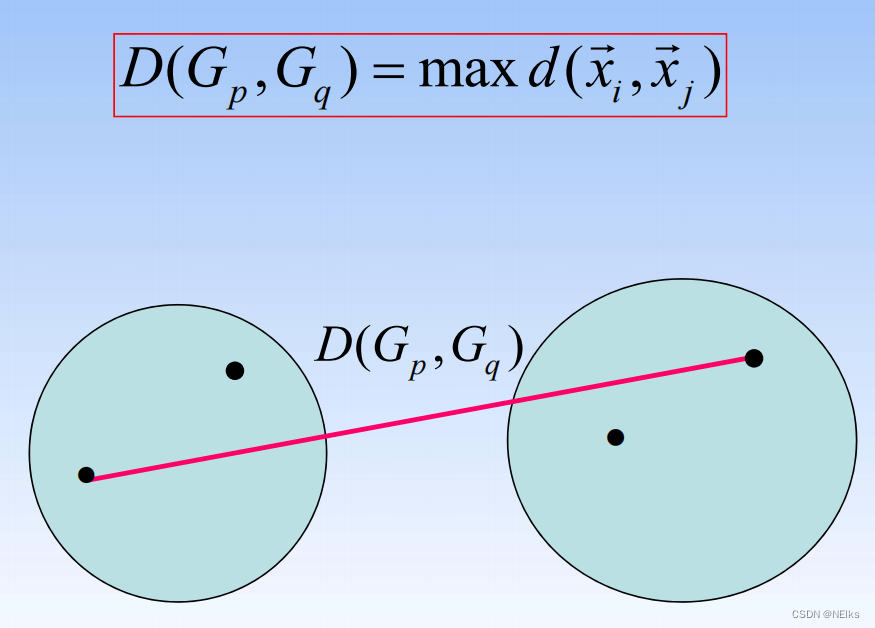
最长距离法:
(Furthest Neighbor)
组间平均连接法:
(Between-group Linkage)
组内平均连接法
(Within-group Linkage)
重心法:
(Centroid clustering)

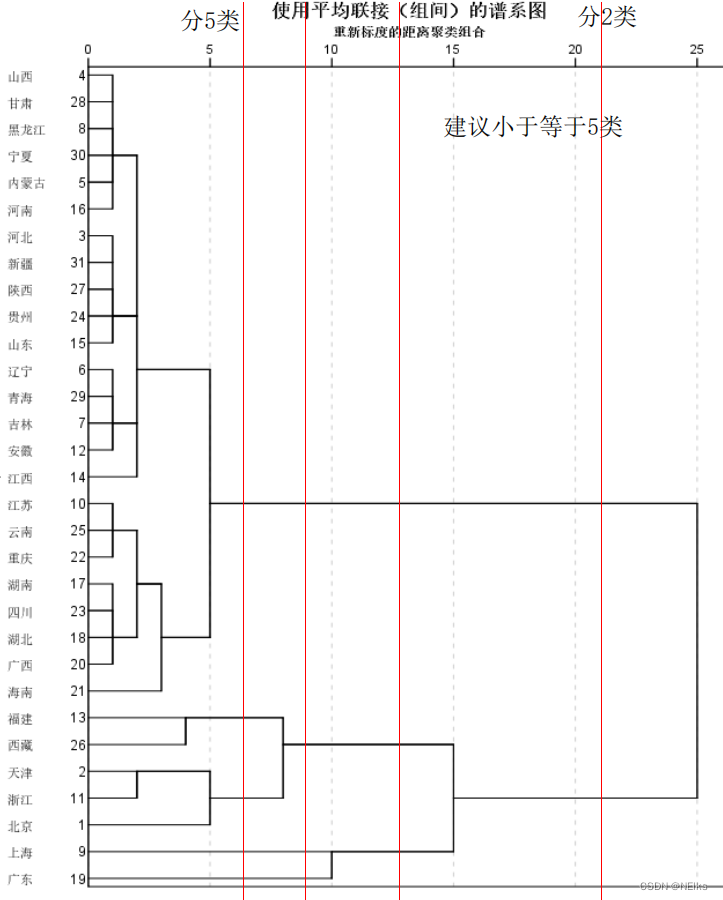
SPSS
聚类谱系图(树状图)
如何确定 K 值 - 肘部法则
聚合系数:总畸变程度
种类数 K 越大,聚合系数 J 越小
SPSS生成历次迭代的表后,有个系数列对应J,阶段对应K;再使用excel作图,并解释:
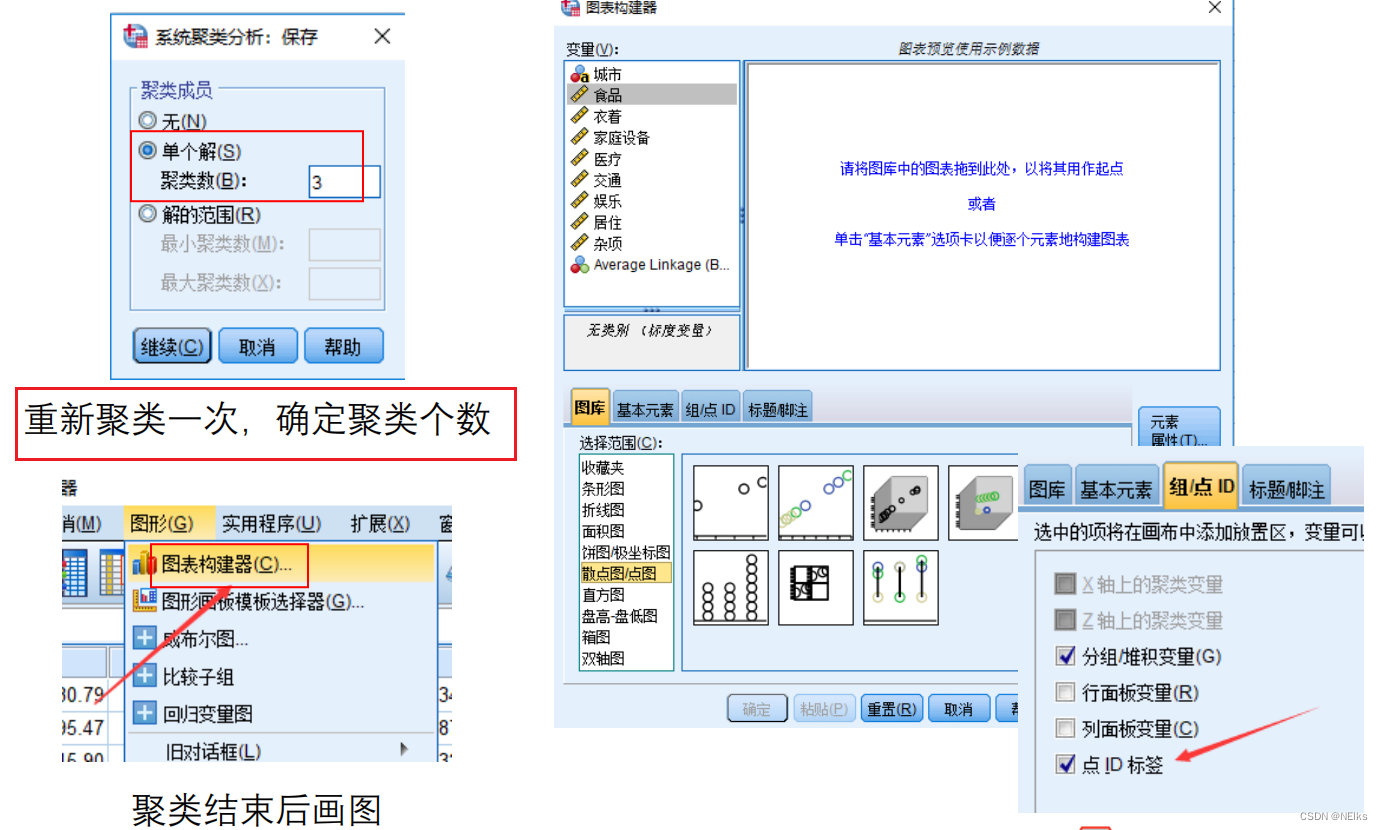
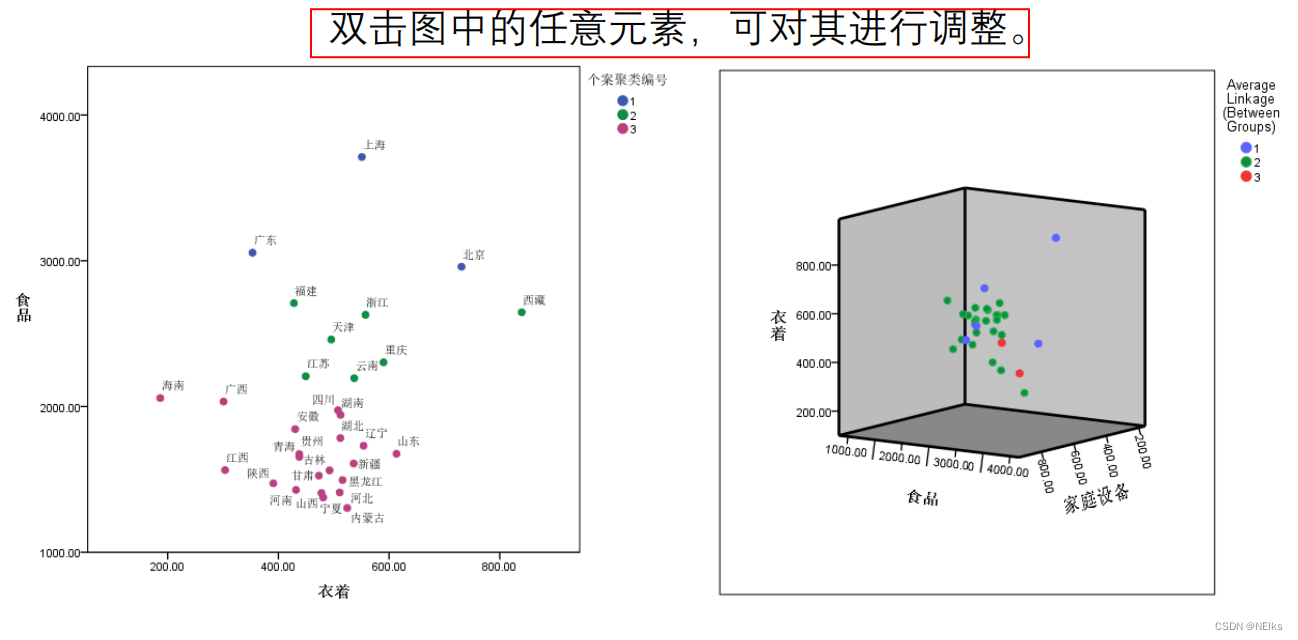
确定K后用SPSS作图
指标为 2/3 个时,才能这样作图
确定 K 后,重新用系统聚类一次,在“保存”中填入聚类个数为 K
DBSCAN算法-基于密度的聚类方法
前两个算法是基于距离的,DBSCAN:具有噪声的基于密度的聚类方法
DBSCAN
算法将数据点分为三类:
- 核心点:在半径Eps内含有不少于MinPts数目的点
- 边界点:在半径Eps内点的数量小于MinPts,但是落在核心点的邻域内
- 噪音点:既不是核心点也不是边界点的点(以某点为圆心作圆,若包括的点<minPts 且该点不在任何核心点范围内,则是噪声)
优点:
1. 基于密度定义,能处理任意形状和大小的簇;
2. 可在聚类的同时发现异常点;
3. 与K-means比较起来,不需要输入要划分的聚类个数。
缺点:
1. 对输入参数 ε 半径 和 Minpts 敏感,确定参数困难;
2. 由于DBSCAN算法中,变量ε和Minpts是全局唯一的,当聚类的密度不均匀时,聚
类距离相差很大时,聚类质量差;
3. 当数据量大时,计算密度单元的计算复杂度大。
只有两个指标,且做出散点图后发现数据表现得很“
DBSCAN
”,这时候再用DBSCAN
进行聚类