给出两棵二叉搜索树的根节点 root1 和 root2 ,请你从两棵树中各找出一个节点,使得这两个节点的值之和等于目标值 Target。
如果可以找到返回 True,否则返回 False。
示例 1:
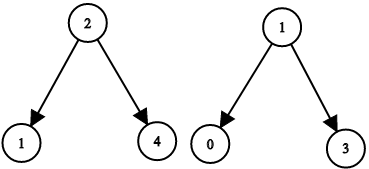
输入:root1 = [2,1,4], root2 = [1,0,3], target = 5 输出:true 解释:2 加 3 和为 5 。
示例 2:
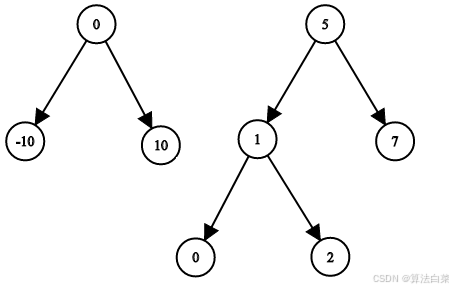
输入:root1 = [0,-10,10], root2 = [5,1,7,0,2], target = 18 输出:false
提示:
- 每棵树上节点数在
[1, 5000]范围内。 -10^9 <= Node.val, target <= 10^9
提示 1
How can you reduce this problem to the classical Two Sum problem?
提示 2
Do an in-order traversal of each tree to convert them to sorted arrays.
提示 3
Solve the classical Two Sum problem.
二叉树的遍历主要有三种:
(1)先(根)序遍历(根左右)
(2)中(根)序遍历(左根右)
(3)后(根)序遍历(左右根)
解法1:DFS先序遍历 + 哈希表
我们可以对每棵树执行遍历,并将值添加到各自的列表 list1 和 list2。然后,我们使用循环遍历list1 将值 list1[i] 存到哈希表中,然后循环遍历list2 ,查找哈希表中是否存在 target - list2[i] , 如果是,我们可以返回 true。
算法步骤
- 创建两个空列表 list1 和 list2。
- 对 root1 执行深度优先搜索(DFS),将每个节点的值添加到 list1 中,对 root2 执行 DFS,并将每个节点的值添加到 list2 中。
- 迭代 list1 中的元素,对于每个元素 value1 存到哈希表中,我们在list2 上进行迭代,寻找 target - value2。
- 如果 target - value2 在 哈希表中存在,返回 True。
- 否则,继续下一个 list2 的元素。
- 如果在嵌套迭代中找不到有效的配对,则返回 False。
Java版:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean twoSumBSTs(TreeNode root1, TreeNode root2, int target) {
List<Integer> list1 = new ArrayList<>();
List<Integer> list2 = new ArrayList<>();
dfs(root1, list1);
dfs(root2, list2);
Map<Integer, Integer> map = new HashMap<>();
for (int num1: list1) {
map.merge(num1, 1, Integer::sum);
}
for (int num2: list2) {
if (map.containsKey(target - num2)) {
return true;
}
}
return false;
}
private void dfs(TreeNode node, List<Integer> list) {
if (node == null) {
return;
}
list.add(node.val);
dfs(node.left, list);
dfs(node.right, list);
}
}Python3版:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def twoSumBSTs(self, root1: Optional[TreeNode], root2: Optional[TreeNode], target: int) -> bool:
def dfs(node, list1):
if not node:
return
list1.append(node.val)
dfs(node.left, list1)
dfs(node.right, list1)
list1, list2 = [], []
dfs(root1, list1)
dfs(root2, list2)
dic = {}
for val in list1:
if val in dic:
dic[val] += 1
else:
dic[val] = 1
for val in list2:
if target - val in dic:
return True
return False
复杂度分析
设 m 和 n 分别是两棵树中的节点数。
- 时间复杂度:O(m+n)。我们需要访问两棵树中的每个节点,将每个节点的值收集到两个列表 list1 和list2 中,这需要 O(m+n) 的时间,因为每个节点只会被访问一次。然后,我们再次循环遍历这两个列表。循环的时间复杂度在为 O(m+n)。
- 空间复杂度:O(m+n)。我们将每个节点的值保存在两个列表 list1 和 list2 中。
解法2:DFS先序遍历 + 二分查找
先前的解决方案没有充分利用二叉搜索树的特性:
- 节点的左子树仅包含值小于节点值的节点。
- 右子树仅包含值大于节点值的节点。
因此,我们可以遍历 root1 的所有节点,并对每个值 value1 进行处理。对于每个值 value1,我们需要在另一棵树 root2 中找到值为 target - value1 的节点,这可以使用二分搜索实现:
- 如果 node.val == target - value1,表示找到一个有效的配对。返回 true。
- 如果 node.val < target - value1,表示 target - value1 可能在 node 的右子树中,因此我们移动到其右孩子。
- 如果 node.val > target - value1,表示 target - value1 可能在 node 的左子树中,因此我们移动到其左孩子。
- 如果找不到 target - value1,我们将继续移动到 root1 中的下一个节点,并重复二分搜索。
算法步骤
- 使用深度优先搜索(DFS)遍历 root1。
- 对于 root1 的每个节点,我们在 root2 上搜索值为 target - value1 的节点。对于 root2 上的每个节点 node2:
- 如果 node2.val = target - value1,表示找到一对,返回 True。
- 如果 node2.val < target - value1,我们移动到 node2 的右子树。
- 如果 node2.val > target - value1,我们移动到 node2 的左子树。
- 如果在 root2 上找不到 target - value1,则继续移动到 root1 的下一个节点。
- 如果在嵌套迭代中找不到有效的配对,则返回 False。
Java版:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean twoSumBSTs(TreeNode root1, TreeNode root2, int target) {
return dfs(root1, root2, target);
}
private boolean dfs(TreeNode root1, TreeNode root2, int target) {
if (root1 == null) {
return false;
}
if (binarySearch(root2, target - root1.val)) {
return true;
}
return dfs(root1.left, root2, target) || dfs(root1.right, root2, target);
}
private boolean binarySearch(TreeNode root2, int target2) {
if (root2 == null) {
return false;
}
if (root2.val == target2) {
return true;
} else if (root2.val < target2) {
return binarySearch(root2.right, target2);
} else {
return binarySearch(root2.left, target2);
}
}
}Python3版:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def twoSumBSTs(self, root1: Optional[TreeNode], root2: Optional[TreeNode], target: int) -> bool:
return self.dfs(root1, root2, target)
def dfs(self, root1: Optional[TreeNode], root2: Optional[TreeNode], target: int) -> bool:
if not root1:
return False
if self.binarySearch(root2, target - root1.val):
return True
return self.dfs(root1.left, root2, target) or self.dfs(root1.right, root2, target)
def binarySearch(self, root2: Optional[TreeNode], target2: int) -> bool:
if not root2:
return False
if root2.val == target2:
return True
elif root2.val < target2:
return self.binarySearch(root2.right, target2)
else:
return self.binarySearch(root2.left, target2)复杂度分析
设 m 和 n 分别是两棵树中的节点数。
- 时间复杂度:O(m⋅logn)。root1 中的每个节点只被访问一次。对于每个 value1,我们在 root2 中搜索 target - value1,平均搜索步骤为 O(h),其中 h 是树的高度。假设两棵树都是平衡的,则 root1 和 root2 的高度分别为 O(logm) 和 O(logn)。
- 空间复杂度:O(logm+logn)。二叉树上的深度优先搜索(DFS)的空间复杂度为 O(h),其中 h 是树的高度。这是因为 DFS 算法使用调用栈来跟踪它访问过的节点,调用栈的最大大小与 DFS 树的高度成正比。假设两棵树都是平衡的,则 root1 和 root2 的高度分别为 O(logm) 和 O(logn)。
解法3:DFS先序遍历 + 哈希集
在解法1中,我们将两棵树的值保存在两个列表中。然后再将 list1 的值存到哈希表中,但是我们不需要计算符合要求的个数,只需要找到是否有符合要求的答案,因此可以用哈希集来查找。
我们将每个节点的值收集到 set1 中,然后将 root2 中的每个节点的值收集到 set2 中。然后,我们迭代 set1 中的每个元素,并查找 target - value1 是否在哈希集 set2 中。
算法步骤
- 创建两个空的哈希集 set1 和set2。
- 对 root1 进行遍历,并将每个节点的值添加到 set1 中,对 root2 进行遍历,并将每个节点的值添加到 set2 中。
- 迭代 set1 中的元素,对于每个元素 value1,检查 target - value1 是否在 set2 中。
- 如果 target - value1 在 set2 中,返回 True。
- 否则,继续下一个 set1 的元素。
- 如果在迭代中找不到有效的配对,则返回 False。
Java版:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean twoSumBSTs(TreeNode root1, TreeNode root2, int target) {
Set<Integer> set1 = new HashSet<>();
Set<Integer> set2 = new HashSet<>();
dfs(root1, set1);
dfs(root2, set2);
for (int val: set1) {
if (set2.contains(target - val)) {
return true;
}
}
return false;
}
private void dfs(TreeNode root, Set<Integer> set) {
if (root == null) {
return;
}
set.add(root.val);
dfs(root.left, set);
dfs(root.right, set);
}
}Python3版:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def twoSumBSTs(self, root1: Optional[TreeNode], root2: Optional[TreeNode], target: int) -> bool:
def dfs(root, set1):
if not root:
return
set1.add(root.val)
dfs(root.left, set1)
dfs(root.right, set1)
set1, set2 = set(), set()
dfs(root1, set1)
dfs(root2, set2)
for val in set1:
if target - val in set2:
return True
return False复杂度分析
设 m 和 n 分别是两棵树中的节点数。
- 时间复杂度:O(m+n)。我们需要访问两棵树中的每个节点,将每个节点的值收集到两个哈希集 set1 和 set2 中,这需要 O(m+n) 的时间,因为每个节点只会被访问一次,而在哈希集上的添加操作需要 O(1) 的时间。我们在 set1 中进行迭代,其中包含 O(m) 步,每一步都检查 set2 中是否存在 target - value1,这需要 O(1) 的时间。
- 空间复杂度:O(m+n)。我们将每个节点的值保存在两个哈希集 set1 和 set2 中。
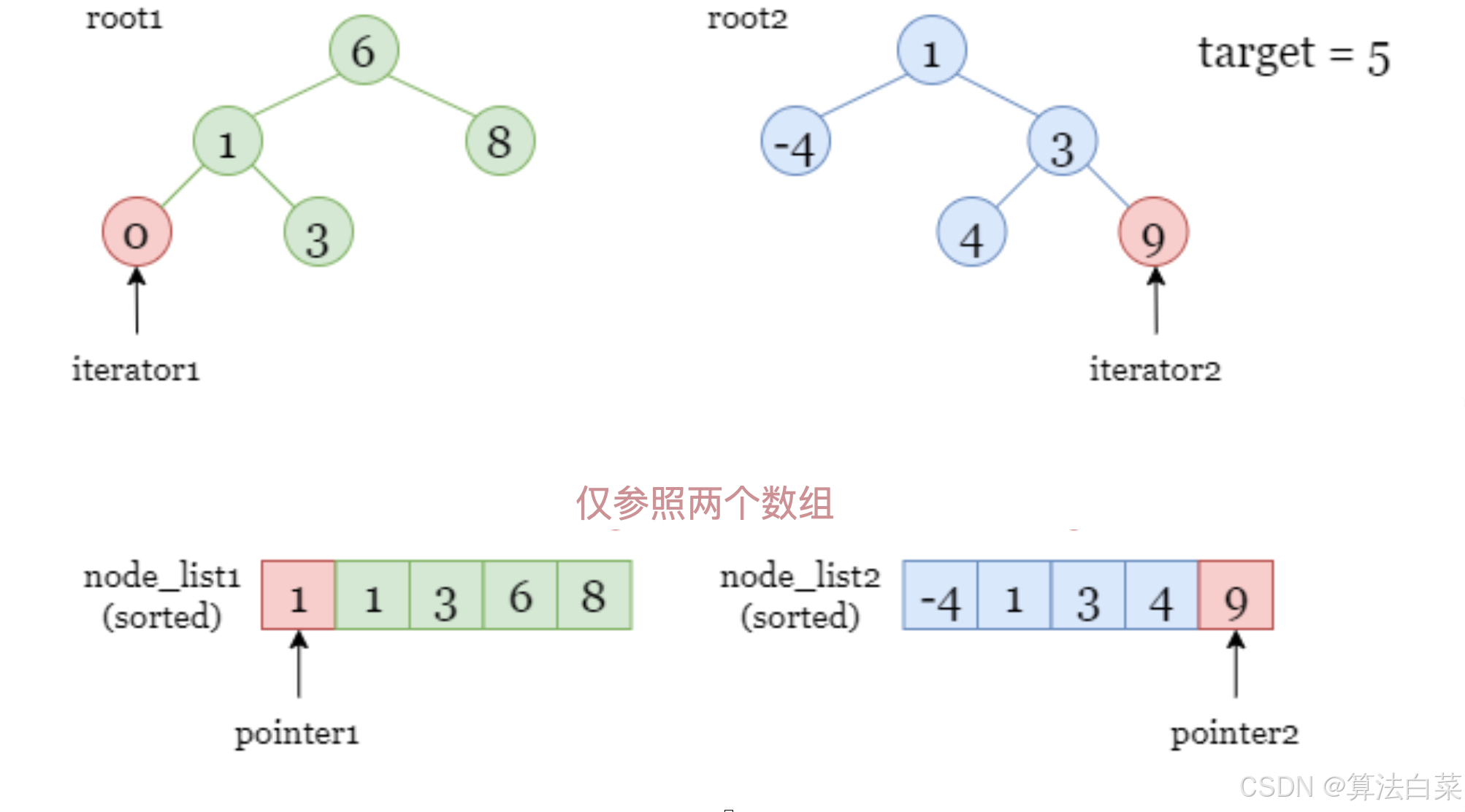
解法4:DFS中序遍历 + 双指针
在二叉搜索树中,中序遍历按照排序顺序访问节点。这是因为我们一直向左移动(较小的值),直到不能再移动为止。一旦完成左子树的遍历,我们才会向右移动(较大的值)。
这意味着我们可以对 root1 和 root2 进行中序遍历,并将每个节点的值收集到 list1 和 list2 中,因此这两个列表已经是排序的。
- 为了找到一个有效的和为 target 的配对,我们可以使用两个指针 l 和 r,它们分别指向 list1 的第一个(最小的)元素和 list2 的最后一个(最大的)元素。
- 然后,我们不断比较 value1 = list1[l] 和 value2 = list2[r] 的和与 target:
- 如果 value1 + value2 = target,这意味着存在一个和为 target 的配对。
- 如果 value1 + value2 < target,我们需要更大的 value1 或更大的 value2。然而,我们在倒序遍历 list2,这意味着我们已经尝试过所有大于 value2 的值,list2 中没有可能的候选值,因此我们必须尝试更大的 value1,将 pointer1 增加 1。
- 如果 value1 + value2 > target,我们需要更小的 value1 或更小的 value2。类似地,由于我们按升序遍历 list1,我们已经尝试过所有小于 value1 的值,因此我们只能尝试更小的 value2,将 r 减少 1。
算法步骤
- 创建两个空列表 list1 和 list2。
- 对 root1 进行中序遍历,将每个节点的值添加到 list1 中,对 root2 进行中序遍历,将每个节点的值添加到 list2 中。
- 初始化两个指针 l = 0 和 r= len(list2) - 1,它们分别指向 list1 的第一个元素和 list2 的最后一个元素。
- 当 l < len(list1) 且 r >= 0 时,我们将 list1[l] + list2[r] 与 target 进行比较:
- 如果 list1[l] + list2[r] = target,返回 True。
- 如果 list1[l] + list2[r] < target,将 l 增加 1。
- 如果 list1[l] + list2[r] > target,将 r 减少 1。
- 如果在迭代后找不到有效的配对,则返回 False。
Java版:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean twoSumBSTs(TreeNode root1, TreeNode root2, int target) {
List<Integer> list1 = new ArrayList<>();
List<Integer> list2 = new ArrayList<>();
dfs(root1, list1);
dfs(root2, list2);
int l = 0;
int r = list2.size() - 1;
while (l < list1.size() && r >= 0) {
if (list1.get(l) + list2.get(r) == target) {
return true;
} else if (list1.get(l) + list2.get(r) < target) {
l++;
} else {
r--;
}
}
return false;
}
private void dfs(TreeNode node, List<Integer> list) {
if (node == null) {
return;
}
dfs(node.left, list);
list.add(node.val);
dfs(node.right, list);
}
}Python3版:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def twoSumBSTs(self, root1: Optional[TreeNode], root2: Optional[TreeNode], target: int) -> bool:
def dfs(node, list1):
if not node:
return
dfs(node.left, list1)
list1.append(node.val)
dfs(node.right, list1)
list1, list2 = [], []
dfs(root1, list1)
dfs(root2, list2)
l, r = 0, len(list2) - 1
while l < len(list1) and r >= 0:
if list1[l] + list2[r] == target:
return True
elif list1[l] + list2[r] < target:
l += 1
else:
r -= 1
return False复杂度分析
设 m 和 n 分别是两棵树中的节点数。
- 时间复杂度:O(m+n)。我们需要访问两棵树中的每个节点,将每个节点的值收集到两个列表 node_list1 和 node_list2 中,这需要 O(m+n) 的时间,因为每个节点只会被访问一次。在 while 循环中,两个指针只朝一个方向移动,每个元素只会被访问一次,因此此迭代需要 O(m+n) 的时间。
- 空间复杂度:O(m+n)。我们将每个节点的值保存在两个列表 node_list1 和 node_list2 中。
解法5:Morris遍历 + 迭代器 双指针
回顾具有 O(h) 空间复杂度(其中 h 是树的高度)的 DFS 解决方案,让我们思考为什么我们需要这么多的空间:
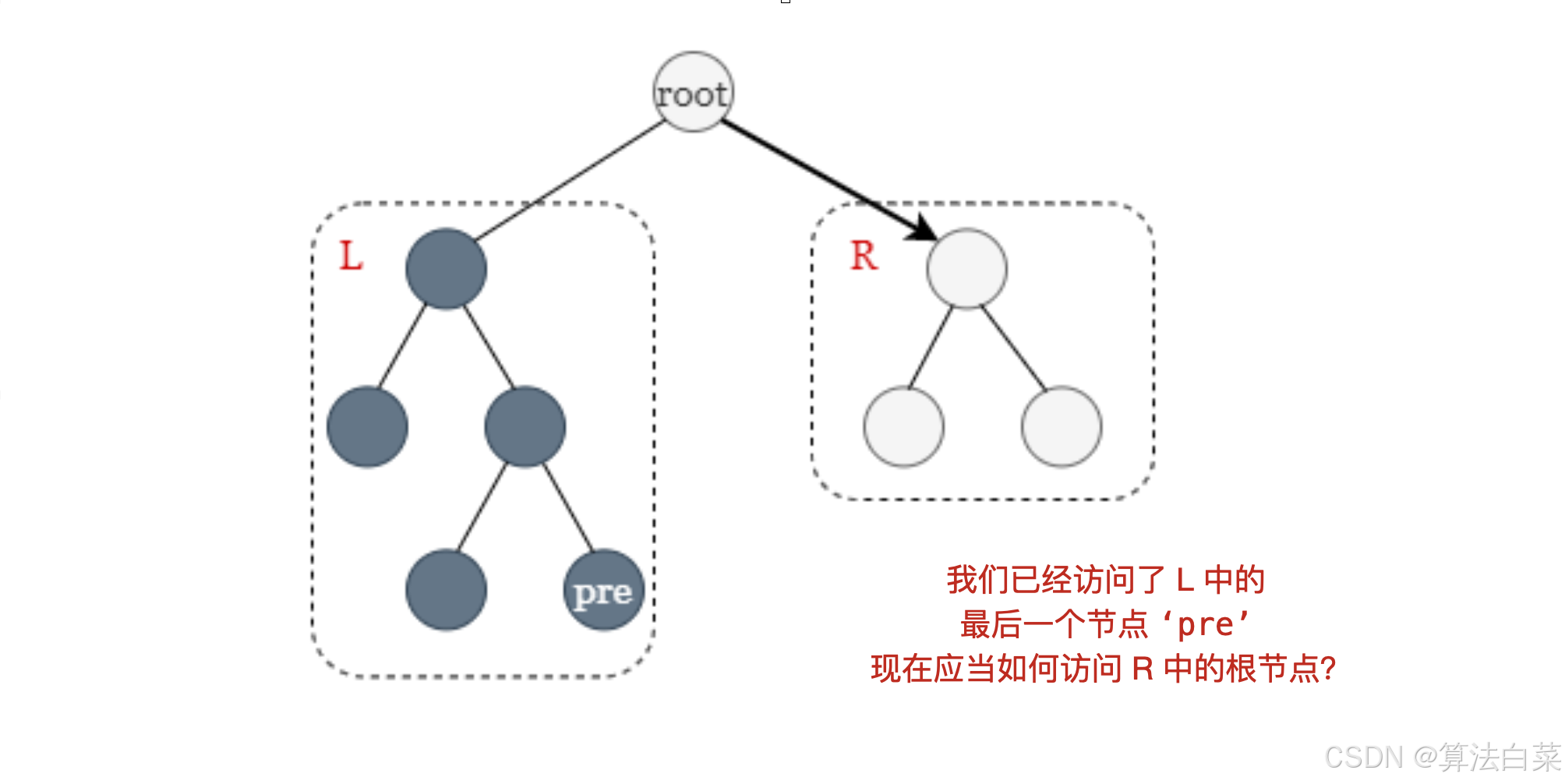
想象一下我们在中序遍历的中间,当前的根节点 root 有左右子树。当我们完成访问左子树的最后一个节点 pre 时,我们希望继续访问 root 和 root 的右子树,但是该如何做呢?
这种方法需要 O(h) 空间,因为我们需要追踪所有先前的根节点,以便我们可以始终在完成访问根节点的左子树时返回该根节点并访问其右子树。栈在递归路径上保存了 h 个节点,以便我们可以回溯到根节点 root。
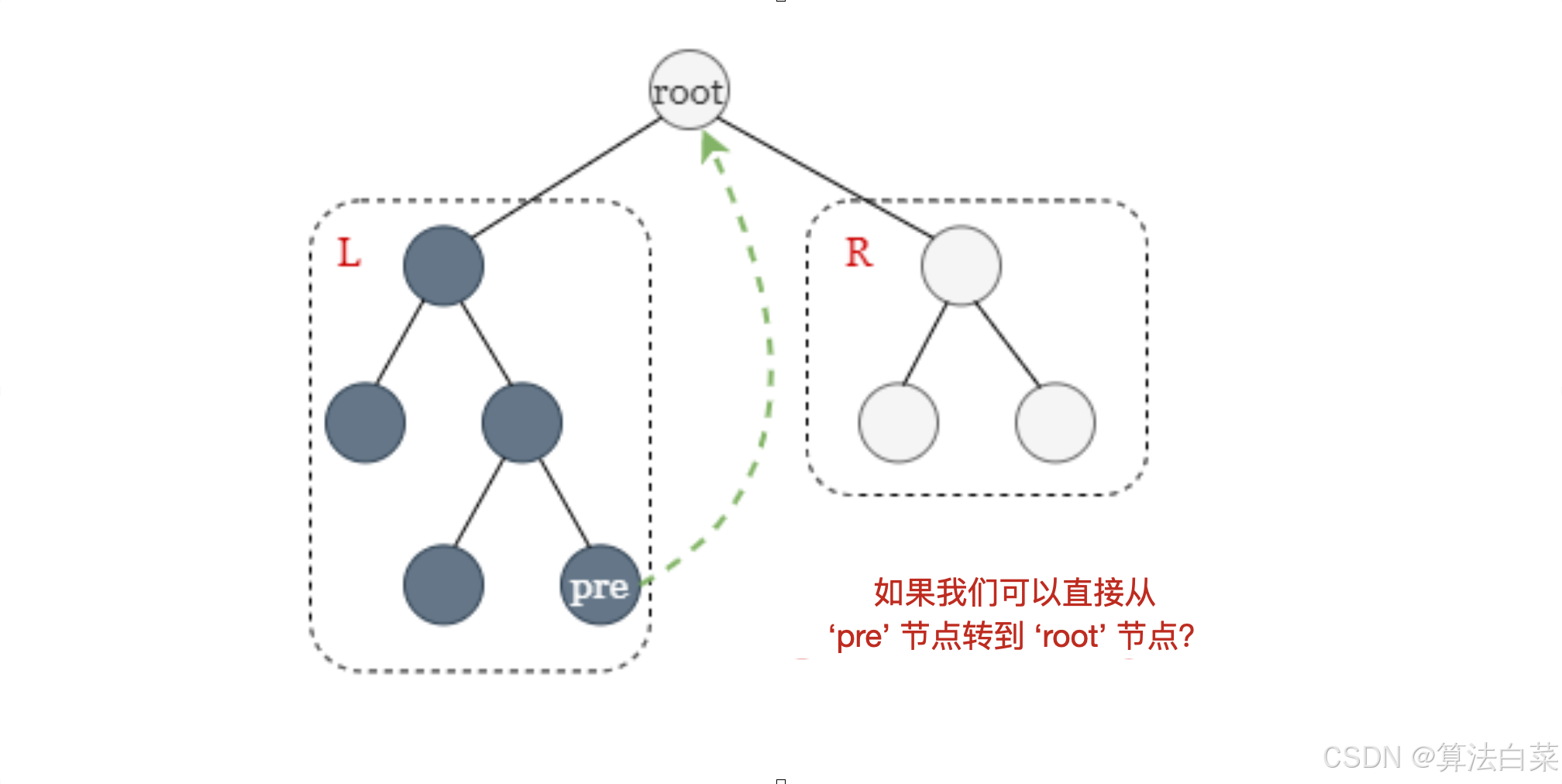
我们可以修改树,以避免使用这些额外的空间。注意,节点 pre 始终没有右子节点,因此我们可以将 root 设为其右子节点!如此,每当我们完成访问 pre 时,我们只需访问其右子节点并返回到 root!
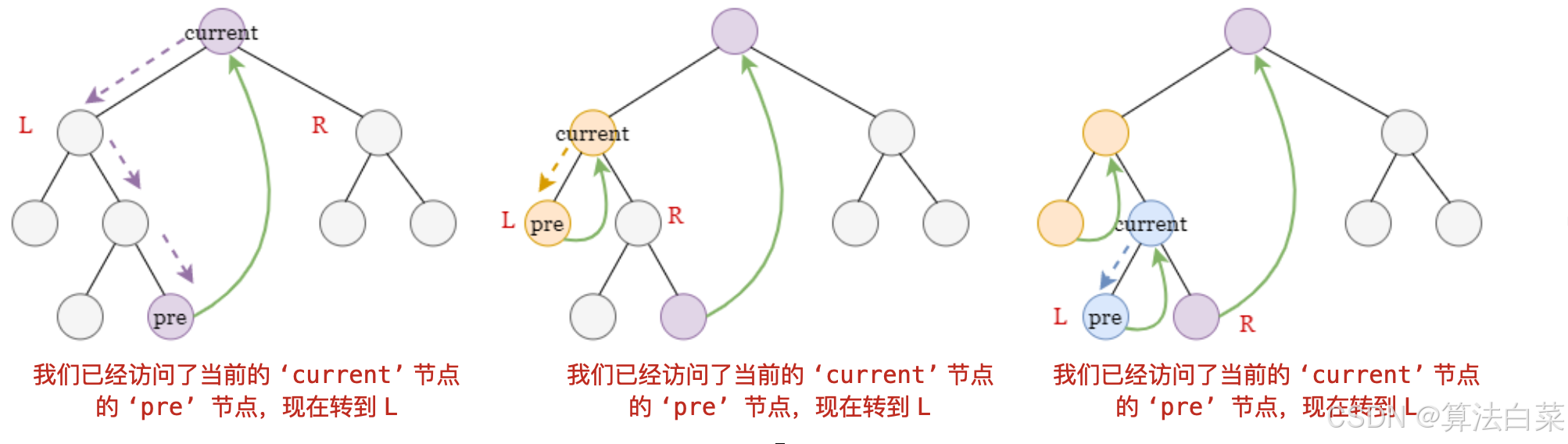
节点 current 的节点 pre 是 current 左子树中最右边的节点。因此,我们可以递归地找到 current 的 pre 节点,并修改 pre 的右指针指向 current 。然后继续移动到 current 的左子节点。
在下一次遍历中,如果我们发现节点 pre 有一个右子节点,这意味着我们以前对其进行了修改,并且我们可以通过简单访问 pre.right 返回到节点 current。然后,我们将 pre 的右指针重置为空。
我们不需要一个辅助栈来存储递归路径上的节点,因此只需要 O(1) 的空间。
morris遍历是二叉树遍历算法的至强算法,不同于递归,非递归(栈实现)的空间复杂度,morris遍历可以将非递归遍历中的树的深度的空间开销,降为O(1)。从而实现时间复杂度为O(n),而空间复杂度为O(1)的精妙算法。
morris遍历利用的是树的叶节点左右孩子为空,这一特性来实现空间开销的极度缩减。
morris遍历的实现原则
- 来到当前节点,记为cur(引用)
- 如果cur无左孩子,cur向右移动(cur = cur.right)
- 如果cur有左孩子,找到cur左子树上最右的节点,记为pre
- 如果 pre 的right指针指向空,让其指向cur,cur向左移动(cur = cur.left)
- 如果 pre 的right指针指向cur,让其指向空,cur向右移动(cur = cur.right)
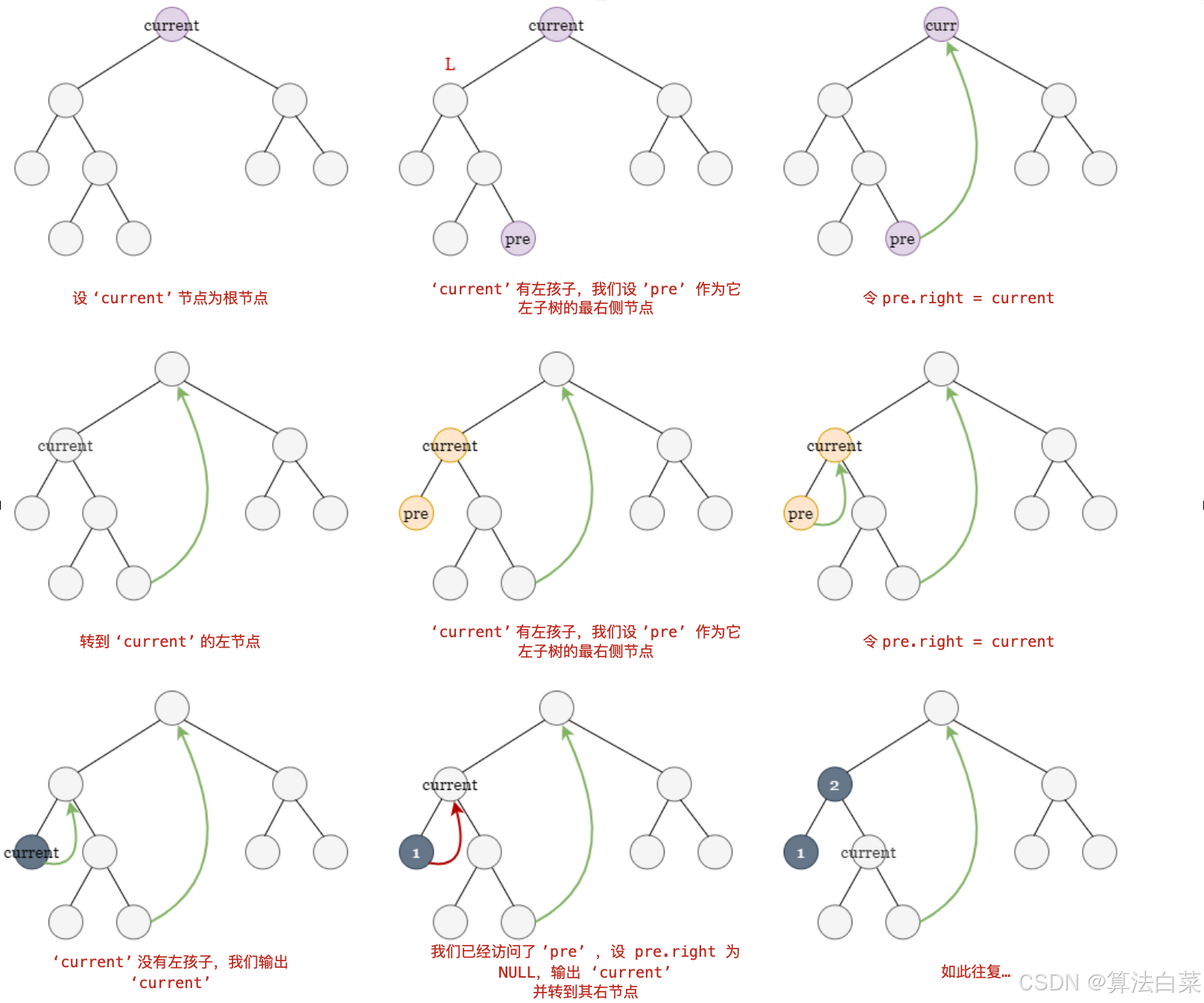
以下图示为例,说明我们如何实现中序 Morris 遍历。
这个解决方案涉及修改原始的二叉搜索树。
现在我们有了一种通过中序 Morris 遍历二叉树的方法,我们可以使用类似于解法4的双指针方法,在两个排序列表上使用两个指针。具体而言,让 l 指向 list1 的第一个元素,r 指向 list2 的最后一个元素。同样,我们使用中序 Morris 遍历创建两个迭代器,分别用于 root1 和 root2:
- iterator1 执行 root1 的中序 Morris 遍历,使得访问的节点值按升序排列。
- iterator2 执行 root2 的反向中序 Morris 遍历,使得访问的节点值按降序排列。
要实现反向中序 Morris 遍历,我们只需在左侧之前遍历右侧,这样会首先得到最大的值。
现在我们可以开始比较正在访问的两个节点的值之和与 target,这与先前的方法类似,我们比较两个指针的值之和是否等于 target:
- 如果 value1 + value2 == target,表示我们找到了一个有效的对,返回 True。
- 如果 value1 + value2 < target,我们应该在 root1 中寻找一个更大的值,因此将 iterator1 移动到下一个节点(比 value1 大的节点)。
- 如果 value1 + value2 > target,我们应该在 root2 中寻找一个更小的值,因此将 iterator2 移动到下一个节点(比 value2 小的节点)。
算法步骤
构建两个迭代器 iterator1 和 iterator2,它们分别执行 root1 的中序 Morris 遍历和 root2 的反向中序 Morris 遍历。
- 从 root1 的最小元素和 root2 的最大元素开始。
- 当两个迭代器都有非空值时,我们将 value1 + value2 与 target 进行比较:
- 如果 value1 + value2 = target,返回 True。
- 如果 value1 + value2 < target,移到 iterator1 的下一个节点。
- 如果 value1 + value2 > target,移到 iterator2 的下一个节点。
- 如果在迭代后找不到有效的对,返回 False。
Java版:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean twoSumBSTs(TreeNode root1, TreeNode root2, int target) {
MorrisIterator iterator1 = new MorrisIterator(root1);
ReverseMorrisIterator iterator2 = new ReverseMorrisIterator(root2);
int value1 = iterator1.next();
int value2 = iterator2.next();
while (value1 != Integer.MIN_VALUE && value2 != Integer.MIN_VALUE) {
if (value1 + value2 == target) {
return true;
} else if (value1 + value2 < target) {
if (iterator1.hasNext()) {
value1 = iterator1.next();
} else {
value1 = Integer.MIN_VALUE;
}
} else {
if (iterator2.hasNext()) {
value2 = iterator2.next();
} else {
value2 = Integer.MIN_VALUE;
}
}
}
return false;
}
}
class MorrisIterator implements Iterator<Integer> {
private TreeNode cur;
private TreeNode pre;
public MorrisIterator(TreeNode root) {
cur = root;
pre = null;
}
public boolean hasNext() {
return cur != null;
}
public Integer next() {
Integer val = null;
while (cur != null) {
if (cur.left == null) {
val = cur.val;
cur = cur.right;
break;
} else {
pre = cur.left;
while (pre.right != null && pre.right != cur) {
pre = pre.right;
}
if (pre.right == null) {
pre.right = cur;
cur = cur.left;
} else {
// pre.right == cur
pre.right = null;
val = cur.val;
cur = cur.right;
break;
}
}
}
return val;
}
}
class ReverseMorrisIterator implements Iterator<Integer> {
private TreeNode cur;
private TreeNode pre;
public ReverseMorrisIterator(TreeNode root) {
cur = root;
pre = null;
}
public boolean hasNext() {
return cur != null;
}
public Integer next() {
Integer val = null;
while (cur != null) {
if (cur.right == null) {
val = cur.val;
cur = cur.left;
break;
} else {
pre = cur.right;
while (pre.left != null && pre.left != cur) {
pre = pre.left;
}
if (pre.left == null) {
pre.left = cur;
cur = cur.right;
} else {
// pre.left == cur
pre.left = null;
val = cur.val;
cur = cur.left;
break;
}
}
}
return val;
}
}Python3版:
在 Python 中,关键字 yield 在生成器的上下文中使用,生成器是迭代器的一种类型。迭代器是一种可以被迭代(即循环)并一次返回一个值的对象。迭代器的优势在于它允许我们处理大量的数据,而无需将所有数据存储在内存中,这对于解决这个问题尤其有用。
当我们使用中序 Morris 遍历遍历两个树时,我们只需要两个当前节点的值。通过在 Morris 遍历中使用关键字 yield,我们可以一次返回二叉树的一个节点,而无需保存所有节点在内存中。
一个带有 yield 的函数就是一个 generator,它和普通函数不同,生成一个 generator 看起来像函数调用,但不会执行任何函数代码,直到对其调用 next()(在 for 循环中会自动调用 next())才开始执行。虽然执行流程仍按函数的流程执行,但每执行到一个 yield 语句就会中断,并返回一个迭代值,下次执行时从 yield 的下一个语句继续执行。看起来就好像一个函数在正常执行的过程中被 yield 中断了数次,每次中断都会通过 yield 返回当前的迭代值。
yield 的好处是显而易见的,把一个函数改写为一个 generator 就获得了迭代能力,比起用类的实例保存状态来计算下一个 next() 的值,不仅代码简洁,而且执行流程异常清晰。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def twoSumBSTs(self, root1: Optional[TreeNode], root2: Optional[TreeNode], target: int) -> bool:
iterator1 = self.morrisTraversal(root1)
iterator2 = self.reverseMorrisTraversal(root2)
value1 = next(iterator1, None)
value2 = next(iterator2, None)
while value1 is not None and value2 is not None:
if value1 + value2 == target:
return True
elif value1 + value2 < target:
value1 = next(iterator1, None)
else:
value2 = next(iterator2, None)
return False
def morrisTraversal(self, root: Optional[TreeNode]) -> None:
cur = root
while cur:
if not cur.left:
yield cur.val
cur = cur.right
else:
pre = cur.left
while pre.right and pre.right != cur:
pre = pre.right
if not pre.right:
pre.right = cur
cur = cur.left
else:
# pre.right == cur
pre.right = None
yield cur.val
cur = cur.right
def reverseMorrisTraversal(self, root: Optional[TreeNode]) -> None:
cur = root
while cur:
if not cur.right:
yield cur.val
cur = cur.left
else:
pre = cur.right
while pre.left and pre.left != cur:
pre = pre.left
if not pre.left:
pre.left = cur
cur = cur.right
else:
# pre.left == cur
pre.left = None
yield cur.val
cur = cur.left
复杂度分析
设 m 和 n 分别表示两棵树中的节点数。
- 时间复杂度: O(m+n)。树中有 n−1 条边(树的定义)。每条边最多被访问两次:首先,在我们找到 'last' 节点时,其次在我们遍历节点时。我们最多访问每个节点 2 次,时间复杂度为 O(n)。参考下面的图片,彩色的边代表在找到 'last' 节点时重新访问的边。在访问每个节点时,除了遍历边缘外,我们执行 O(1) 的工作,因此时间复杂度为 O(n)。我们构建两个迭代器来遍历 root1 和 root2。
- 空间复杂度: O(1)。在 Morris 遍历中,我们需要跟踪两个节点 pre 和 current,它们占用常数空间。由于我们利用了一些叶节点的右子节点,因此不需要额外的空间。反向 Morris 遍历也是一样的。