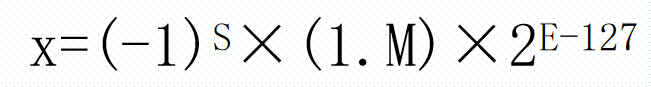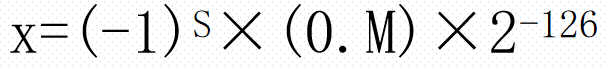我们平时书写的数据如+110、-111称为数的真值,而数在经过特定的方式编码后在计算机中的表示称为数的机器码。为满足计算机中不同操作的要求,对于一个数常见的编码方式有如下几种。
一、原码
(1) 整数的原码表示
从直观上看,整数的原码相对于真值而言就是在数值前添加一位符号位来替代真值中的数值符号,符号位为0表示正数,符号位为1表示负数。
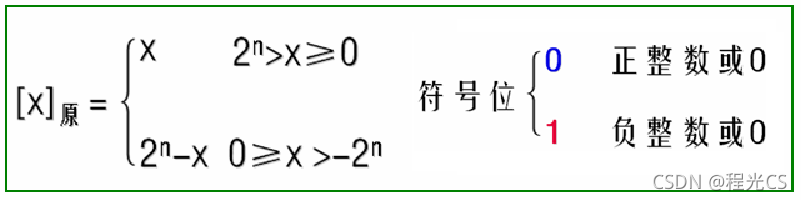
数学定义:
例:+111的原码为0111,-101的原码为1101
(2) 纯小数的原码表示
纯小数的原码首位同样为符号位,后面的数值则表示小数的尾数,纯小数的整数位为默认为0无需表示。
例:+0.111的原码为0111,-0.101的原码为1101
可以看到,+111和+0.111的原码同为0111,这是因为约定的小数点位置不同,整数的原码的小数点约定在末尾,纯小数的原码的小数点约定在数值的最前面,这样通过约定小数点的位置来表示数的方法就称为定点数表示法,约定小数点位置实际上就是约定编码中每一位的权重。
二、反码
正数的反码与其原码相同。
负数的反码是其对应原码的符号位不变,数值位按位取反。
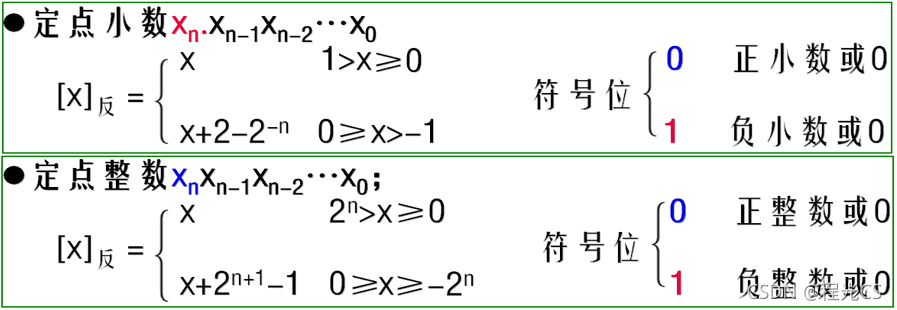
数学定义:
例:
| 真值 | +111 | -101 | +0.111 | -0.101 |
|---|---|---|---|---|
| 原码 | 0111 | 1101 | 0111 | 1101 |
| 反码 | 0111 | 1010 | 0111 | 1010 |
三、补码
原码虽然转换很简单,但是在做减法时操作很复杂(减不够还要借位),因此计算机在做加负数操作时会先将负数的原码转换为补码再做加法。
先举个栗子,假设时钟现在是9点钟,我把时针往回拨3个小时是6点钟,或者顺时针往后拨9个小时还是6点钟,也就是说9-3的结果等同于9+9(mod 12),对于模数12,-3的补码为+9,这就引申出了一种将减法转换为加法的思想,把减去一个正数视为加上一个负数(例如9+(-3)),再将负数转换为对应的补码,最后就可以和补码做加法了,若结果超出了模数则丢弃一个模数即可。
如图所示:9减去灰色的部分(-3)就等同于加上蓝色的部分,即-3的补码即为蓝色部分的长度9(mod 12)。即补码=模数+真值(超出模数则舍弃一个模数)
(1) 整数的补码表示
对于一个n位的二进制真值x,则取模数为2^(n+1),若x为正数则补码和原码相同(加上一个模数又需舍弃一个模数 故相同),若为负数则补码为模数加上x。相对于原码,补码这里的首位就不仅代表原数真值的符号了,也是补码自己的一个数值位。
取模数为2^(n+1)是因为在需要舍弃模数时只需要舍弃运算结果(二进制数)的最高位即可,这在计算机中很容易实现
数学定义:
例:三位二进制数的模数2^4就是10000,故+111的补码为0111(即10000 + 111 = 0111 (舍弃模数位)),-101的补码为1011(即10000 - 101 = 1011)
补码运算示例:那么+111 - 101 = +111 + (-101) = 0111 + 1011 = 10010,运算结果只保留后四位(即舍弃模数位),故计算结果为0010。这样就通过加法实现了减法运算。
补码可表示数据范围:由数学定义可知,n位二进制补码可表示的数据范围为 -2n-1~2n-1-1。以8位的byte类型数为例,可表示的数据范围为 -27~27-1,即-128至+127,最小负数-128(补码:1000 0000),最大负数-1(补码:1111 1111),0(补码:0000 0000),最小正数1(补码:0000 0001),最大正数127(补码:0111 1111)。
由补码求真值:正数的补码即为原码即为真值,负数的真值由计算规则可知 负数真值= - (模数 - 补码),以补码1111 1111为例,其真值 = - (1 0000 0000 - 1111 1111) = - 0000 0001 = -1
(2) 纯小数的补码表示
对于一个纯小数x,则取模数为2^1,正数的补码和原码相同,负数的补码为模数2加上x。同样补码的首位不仅代表原数真值的符号,也是补码的数值位。
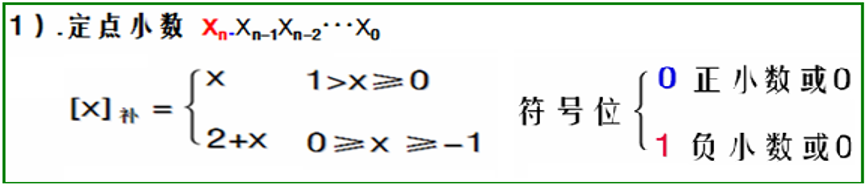
数学定义:
例:纯小数的模数2就是10,故+0.111的补码为0111,-0.101的补码为1011(小数点约定在符号位后)
计算机中求补码的规则
可以注意到求负数的补码时还是要做减法,这在计算机中就很不方便了,但是通过其数学定义可以看到无论是整数还是纯小数,负数的补码都等于反码的末尾加1,而这又等同于原码数值位从右向左遇到第一个1后,这个1左边的数值位都按位取反,故实际计算机中求补码的规则如下:
正数的补码等于原码
负数的补码等于原码的数值位从右向左的第一个1左边的所有数值位按位取反(例:byte类型值-6的原码为1000 0110,则其补码为1111 1010)
四、变形补码
两个补码在运算时可能会溢出从而产生错误的结果,比如0111+0101 = 1100,两个正数相加反而得到了一个负数,那么在计算机中要如何判断运算结果是否溢出了呢,这就引申出了变形补码。从直观上看,相对于补码来说变形补码就是用两位来表示符号位,00表示正数,11表示负数。运算结果符号位为01表示正溢出,10表示负溢出。
(1) 整数的变形补码表示
与补码的不同之处在于,n位二进制整数的变形补码的模数是2^(n+2),比如-111的模数是100000,其变形补码就是11001。
例:原码0111和0101的变形补码分别是00111和00101,其相加的运算结果为01100,符号位为01,计算机就可以判断运算结果正溢出了
(2) 纯小数的变形补码表示
纯小数的变形补码的模数为2^2即100
五、移码
对于一个n位二进制整数,将它加上一个特定的偏置常数(传统定义是加上2^n,确保所有n位负数都能转换为正数)得到的就是移码。这样就可以很方便的比较两个整数的大小,比如要比较两个二进制数-11和+10的大小,将它们同时加上100编码为移码001和110,这样在计算机中就非常容易比较大小了。移码通常用于表示浮点数的阶码。
六、浮点数编码
用前面定点数的方式表示数据很方便也容易理解,但是也有如下缺点
(1) 表示的范围有限
对于一个32位数,用原码或补码这样的定点数表示法最大的整数表示范围就是-(2^31-1) ~ 2^31-1,约正负21亿多,那么当要表示的数超过这个范围就无法表示了
(2)表示的精度有限(3)不方便表示一般小数(如11.011)
故引申出了用浮点数的方式来表示数据的方式
浮点数区别于前面的定点数编码,它是用表示指数的形式来表示数据,如-1.01101 x 2^-101,浮点数编码是用一位表示符号位,用几位表示尾数,用几位表示指数-101。
IEEE754标准格式表示浮点数
浮点数有多种编码方式,其中最常用的就是IEEE754标准中的格式。其中32位短浮点数和64位长浮点数的格式如下
S:符号位。占1位,在最高位,0表示正数,1表示负数。
E:阶码。阶码是用移码的方式来表示正负指数,32位短浮点数中阶码占8位(第30~23位),偏置常数取127,即阶码E为浮点数的指数真值e加上127。
M:尾数。整数部分默认为1无需表示,故只需表示尾数,32位短浮点数中尾数占23位。
IEEE754标准对32位浮点数N有如下定义:
(1) 若E = 255(即阶码全为1)且M不为0,则N = NaN,表示无定义数据
(2) 若E = 255且M=0,N表示无穷大,符号位为0表示正无穷,符号位为1表示负无穷
(3) 若E = 0且M=0,则N表示0,符号位为0表示正零,符号位为1表示负零
(4) 若0<E<255,则N为规格化数,其真值x为:
阶码E的范围为1 ~ 254,故可表示的指数的范围为 -126 ~ +127。因此32位浮点数可表示的绝对值的范围为10^-38 ~ 10^38。
(5) 若E = 0 且M ≠ 0,则N为非规格化数,其真值x为:
对于规格化无法表示的数据,可以用非规格化的形式表示。