1、PID算法理论
1.1、算法介绍
PID，就是对输入偏差进行比例积分微分运算，运算的叠加结果去控制执行机构。公式如下 :

$u(t)=K_p[e(t)+\frac{1}{T_i}{\int }_0^{t}e(t)dt+Td\frac{de(t)}{dt}]$

它由三部分组成：

P 就是比例，就是输入偏差乘以一个系数；
I 就是积分，就是对输入偏差进行积分运算；
D 就是微分，对输入偏差进行微分运算。
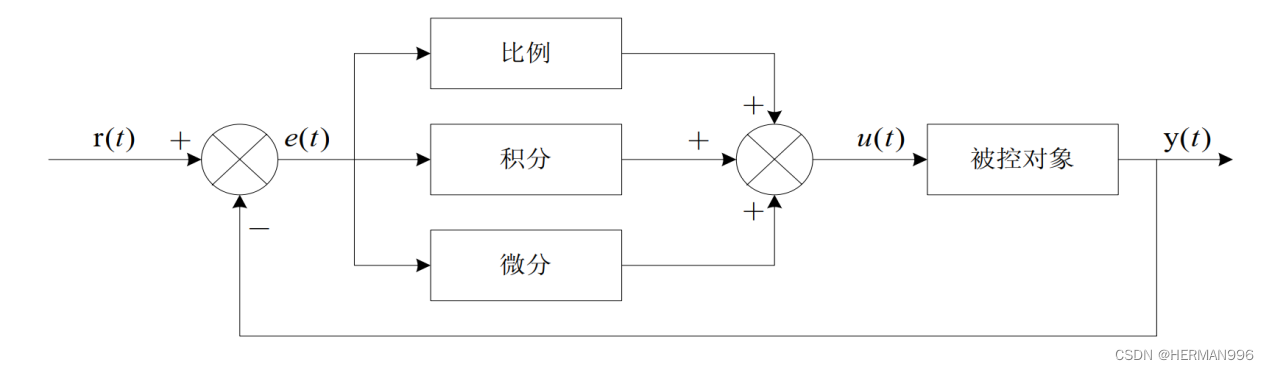
如下图所示就是一个基本的PID控制器：

1.1.1、比例部分
比例部分的数学式表示是： $K_p\ast e(t)$

在模拟 PID 控制器中，比例环节的作用是对偏差瞬间作出反应。偏差一旦产生，控制器立即产生控制作用，使控制量向减少偏差的方向变化。控制作用的强弱取决于比例系数 ，比例系数越大，控制作用越强，则过渡过程越快，控制过程的静态偏差也就越小；但是越大，也越容易产生振荡，破坏系统的稳定性。故而，例系数选择必须恰当，才能过渡时间少，静差小而又稳定的效果。

优点 : 调整系统的开环比例系数，提高系统的稳态精度，减低系统的惰性，加快响应速度。

缺点 : 仅用P控制器,过大的开环比例系数不仅会使系统的超调量增大，而且会使系统稳定裕度变小，甚至不稳定。

1.1.2、积分部分
积分部分的数学式表示是：$\frac{K_p}{T_i}{\int }_0^{t}e(t)dt$
积分常数越大，积分的积累作用越弱，这时系统在过渡时不会产生振荡；但是增大积分常数会减慢静态误差的消除过程，消除偏差所需的时间也较长，但可以减少超调量，提高系统的稳定性。当Ti 较小时，则积分的作用较强，这时系统过渡时间中有可能产生振荡，不过消除偏差所需的时间较短。所以必须根据实际控制的具体要求来确定Ti。

优点：消除稳态误差。

缺点：积分控制器的加入会影响系统的稳定性，使系统的稳定裕度减小。

1.1.3、微分部分
微分部分的数学式表示是：$K_p\ast Td\frac{de(t)}{dt}$

微分环节的作用使阻止偏差的变化。它是根据偏差的变化趋势（变化速度）进行控制。偏差变化的越快，微分控制器的输出就越大，并能在偏差值变大之前进行修正。微分作用的引入，将有助于减小超调量，克服振荡，使系统趋于稳定，特别对髙阶系统非常有利，它加快了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感，对那些噪声较大的系统一般不用微分，或在微分起作用之前先对输入信号进行滤波。微分部分的作用由微分时间常数Td 决定。Td 越大时，则它抑制偏差变化的作用越强；Td越小时，则它反抗偏差 变化的作用越弱。微分部分显然对系统稳定有很大的作用。适当地选择微分常数Td ，可以使微分作用达到最优。

优点：使系统的响应速度变快，超调减小，振荡减轻，对动态过程有“预测”作用。

1.2、PID算法的选择
数字式 PID 控制算法可以分为位置式 PID 和增量式 PID 控制算法。那么我们在决定选择使用那个PID算法之前我们应该先要了解他的原理：

1.2.1、位置式 PID 算法
$u(k)=K_{p}e(k)+K_I{\sum }_{i=o}e(i)+K_D[e(k)-e(k-1)]$

e(k): 用户设定的值（目标值） - 控制对象的当前的状态值

比例P : e(k)

积分I : ∑e(i) 误差的累加

微分D : e(k) - e(k-1) 这次误差-上次误差

也就是位置式PID是当前系统的实际位置，与你想要达到的预期位置的偏差，进行PID控制

因为有误差积分 ∑e(i)，一直累加，也就是当前的输出u(k)与过去的所有状态都有关系，用到了误差的累加值；（误差e会有误差累加），输出的u(k)对应的是执行机构的实际位置，，一旦控制输出出错(控制对象的当前的状态值出现问题 )，u(k)的大幅变化会引起系统的大幅变化并且位置式PID在积分项达到饱和时,误差仍然会在积分作用下继续累积，一旦误差开始反向变化，系统需要一定时间从饱和区退出，所以在u(k)达到最大和最小时，要停止积分作用，并且要有积分限幅和输出限幅所以在使用位置式PID时，一般我们直接使用PD控制

而位置式 PID 适用于执行机构不带积分部件的对象，如舵机和平衡小车的直立和温控系统的控制

优点： 位置式PID是一种非递推式算法，可直接控制执行机构（如平衡小车），u(k)的值和执行机构的实际位置（如小车当前角度）是一 一对应的，因此在执行机构不带积分部件的对象中可以很好应用

缺点： 每次输出均与过去的状态有关，计算时要对e(k)进行累加，运算工作量大。

1.2.2、增量式 PID 算法
$\Delta u(k)=u(k)-u(k-1)=K_P[e(k)-e(k-1)]+K_{i}e(k)+K_D[e(k)-2e(k-1)+e(k-2)]$

比例P : $e(k)-e(k-1)$这次误差-上次误差

积分I : $e(k)$ 误差

微分D : $e(k)-2e(k-1)+e(k-2)$ 这次误差-2*上次误差+上上次误差

增量式PID根据公式可以很好地看出，一旦确定了 KP、TI 、TD，只要使用前后三次测量值的偏差， 即可由公式求出控制增量而得出的控制量$\Delta u(k)$对应的是近几次位置误差的增量，而不是对应与实际位置的偏差 没有误差累加也就是说，增量式PID中不需要累加。控制增量$\Delta u(k)$的确定仅与最近3次的采样值有关，容易通过加权处理获得比较好的控制效果，并且在系统发生问题时，增量式不会严重影响系统的工作

总结：增量型 PID，是对位置型 PID 取增量，这时控制器输出的是相邻两次采样时刻所计算的位置值之差，得到的结果是增量，即在上一次的控制量的基础上需要增加（负值意味减少）控制量。

优点：

①误动作时影响小，必要时可用逻辑判断的方法去掉出错数据。

②手动/自动切换时冲击小，便于实现无扰动切换。当计算机故障时，仍能保持原值。

③算式中不需要累加。控制增量Δu(k)的确定仅与最近3次的采样值有关。

缺点：

② 积分截断效应大，有稳态误差；

②溢出的影响大。有的被控对象用增量式则不太好；

1.2.3、增量式与位置式区别
(1)增量式算法不需要做累加，控制量增量的确定仅与最近几次偏差采样值有关，计算误差对控制 量计算的影响较小。而位置式算法要用到过去偏差的累加值，容易产生较大的累加误差。

(2)增量式算法得出的是控制量的增量，例如在阀门控制中，只输出阀门开度的变化部分，误动作 影响小，必要时还可通过逻辑判断限制或禁止本次输出，不会严重影响系统的工作。 而位置式的输出直接对应对象的输出，因此对系统影响较大。

(3)增量式PID控制输出的是控制量增量，并无积分作用，因此该方法适用于执行机构带积分部件的对象，如步进电机等，而位置式PID适用于执行机构不带积分部件的对象，如电液伺服阀。

(4)在进行PID控制时，位置式PID需要有积分限幅和输出限幅，而增量式PID只需输出限幅

位置式PID和增量式PID只是数字PID控制算法的两种实现形式而已，本质完全相同。主要区别是积分项存储方式不同，位置式PID积分项单独存储，增量式PID积分项作为输出的一部分存储，网上各路玩家也对位置式和增量式的使用上有着自己独特的见解和看法，具体还是看我们具体应用场景适合哪种算法。

1.3、PID参数的调试
PID控制器参数选择的方法很多，例如试凑法、临界比例度法、扩充临界比例度法等。但是，对于PID控制而言，参数的选择始终是一件非常烦杂的工作，需要经过不断的调整才能得到较为满意的控制效果。依据经验，一般PID参数确定的步骤如下：

1.3.1、确定比例系数Kp
确定比例系数Kp时，首先去掉PID的积分项和微分项，可以令Ti=0、Td=0，使之成为纯比例调节。输入设定为系统允许输出最大值的60％～70％，比例系数Kp由0开始逐渐增大，直至系统出现振荡；再反过来，从此时的比例系数Kp逐渐减小，直至系统振荡消失。记录此时的比例系数Kp，设定PID的比例系数Kp为当前值的60％～70％。

1.3.2、确定积分时间常数Ti
比例系数Kp确定之后，设定一个较大的积分时间常数Ti，然后逐渐减小Ti，直至系统出现振荡，然后再反过来，逐渐增大Ti，直至系统振荡消失。记录此时的Ti，设定PID的积分时间常数Ti为当前值的150％～180％。

1.3.3、确定微分时间常数Td
微分时间常数Td一般不用设定，为0即可，此时PID调节转换为PI调节。如果需要设定，则与确定Kp的方法相同，取不振荡时其值的30％。

1.3.4、系统空载、带载联调
对PID参数进行微调，直到满足性能要求。

当然这只是我的个人调试方法，并不一定适合每一个人和每一个环境，仅提供给大家参考;然而网上也流传着调试PID的经典试凑口诀，我也贴出来供大家参考：

            参数整定找最佳， 从小到大顺序查。

            先是比例后积分， 最后再把微分加。

            曲线振荡很频繁， 比例度盘要放大。

            曲线漂浮绕大弯， 比例度盘往小扳。

            曲线偏离回复慢， 积分时间往下降。

            曲线波动周期长， 积分时间再加长。

            曲线振荡频率快， 先把微分降下来。

            动差大来波动慢， 微分时间应加长。

            理想曲线两个波， 前高后低四比一。

            一看二调多分析， 调节质量不会低。

PID是比例§、积分(I)、微分(D)控制算法，并不是必须同时具备这三种算法，也可以是PD,PI,甚至只有P算法控制。我以前对于闭环控制的一个最朴素的想法就只有P控制，将当前结果反馈回来，再与目标相减，为正的话，就减速，为负的话就加速，当然这只是最简单的闭环控制算法，也就还是回到上一节位置式和增量式的总结，具体要参考我们当前的控制环境，因为每个控制系统的差异，能让我们系统达到最稳定效果的参数就固然是OK的。

汇报展示部分：

Proportion Integration Differentiation控制调节

对输入偏差进行比例积分微分运算，运算的叠加结果去控制执行机构。

$u(t)=K_p[e(t)+\frac{1}{T_i}{\int }_0^{t}e(t)dt+Td\frac{de(t)}{dt}]$
PID控制调节由三部分组成：

比例Proportion为输入偏差乘以一个系数；
积分Integration为对输入偏差进行积分运算；
微分Differentiation为对输入偏差进行微分运算。

比例调节环节 $K_p\ast e(t)$
比例环节的作用是对偏差瞬间作出反应。偏差一旦产生，控制器立即产生控制作用，使控制量向减少偏差的方向变化。控制作用的强弱取决于比例系数 ，比例系数越大，控制作用越强，则过渡过程越快，控制过程的静态偏差也就越小，但在开环比例系数过大时，也容易产生振荡，增大超调量，降低系统稳定裕度，破坏系统的稳定性。通过调节恰当的比例部分，实现过渡时间少、静态偏差小、稳定、提高系统的稳态精度，减低系统的惰性，加快响应速度的控制效果。

积分调节环节 $\frac{K_p}{T_i}{\int }_0^{t}e(t)dt$
积分控制器的加入会影响系统的稳定性，使系统的稳定裕度减小。积分常数越大，积分的积累作用越弱，这时系统在过渡时不会产生振荡；但是增大积分常数会减慢静态误差的消除过程，消除偏差所需的时间也较长，但可以减少超调量，提高系统的稳定性。当Ti 较小时，则积分的作用较强，这时系统过渡时间中有可能产生振荡，不过消除偏差所需的时间较短。根据实际控制的具体要求来确定Ti，有利于消除稳态误差。

微分调节环节 $K_p\ast Td\frac{de(t)}{dt}$
微分环节的作用使阻止偏差的变化。它是根据偏差的变化趋势（变化速度）进行控制。偏差变化的越快，微分控制器的输出就越大，并能在偏差值变大之前进行修正。微分作用的引入，将有助于减小超调量，克服振荡，使系统趋于稳定，特别对髙阶系统非常有利，它加快了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感，对那些噪声较大的系统一般不用微分，或在微分起作用之前先对输入信号进行滤波。微分部分的作用由微分时间常数Td 决定。Td 越大时，则它抑制偏差变化的作用越强；Td越小时，则它反抗偏差 变化的作用越弱。微分部分显然对系统稳定有很大的作用。通过选择微分常数Td ，可以使微分作用达到最优，加快系统响应速度，减小超调，减轻震荡，对动态过程有“预测”作用。

增量式 限幅 PID算法

$\Delta u(k)=u(k)-u(k-1)=K_P[e(k)-e(k-1)]+K_{i}e(k)+K_D[e(k)-2e(k-1)+e(k-2)]$

比例P : $e(k)-e(k-1)$这次误差-上次误差

积分I : $e(k)$ 误差

微分D : $e(k)-2e(k-1)+e(k-2)$ 这次误差-2*上次误差+上上次误差

根据增量式PID公式，当确定常量KP、KI、KD数值后，使用前后三次测量值的偏差量，可由公式求出控制增量而得出的控制量$\Delta u(k)$对应的是近几次位置误差的增量，而不是对应与实际位置的偏差，不存在误差累加。也就是说，因为控制增量$\Delta u(k)$的确定仅与最近3次的采样值有关，通过加权处理可以较为方便取得比较好的控制效果，并且在系统发生问题时，增量式不会严重影响系统的工作
增量型 PID，是对位置型 PID 取增量，这时控制器输出的是相邻两次采样时刻所计算的位置值之差，得到的结果是增量，即在上一次的控制量的基础上需要增加/减少控制量。增量式PID存在积分截断效应大，有稳态误差的缺点，当溢出时影响较大，不适用于部分被控对象。同时增量式PID在误动作时影响小，用逻辑判断限幅输出的方法去掉出错数据。